Which number is greater . 84 or 9.3
Answers
Answer:
9.3
Step-by-step explanation:
9.3 is greater because 9.3 has a bigger value than .84 because .84 is in the hundredths place which is less than the unit digit which is 9 from 9.3
Hope this helps!
Related Questions
5. A line passes through (5,-4) and has a slope of - 1/4 Name three points on this line.
Answers
Answer: (9,-5) (1,-3) (-3,-2)
Hope this helps!
The slope intercept form would be y= 1/-4x-11/4
Find the slope of the line between the points (-2, 7) and (10, 3)
Answers
Answer:
m = -1/3
Step-by-step explanation:
What is the largest Angle of BCD?
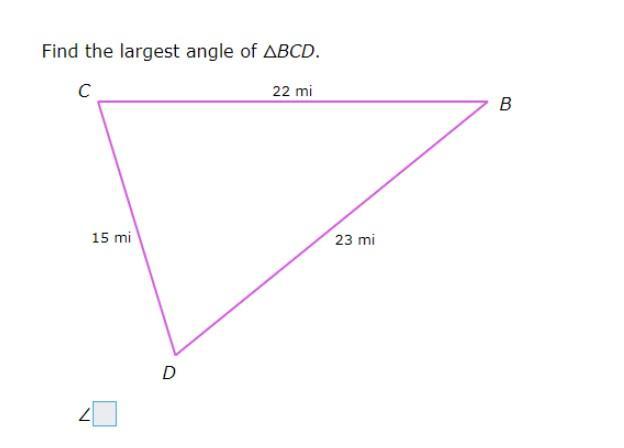
Answers
Answer:
< C
Step-by-step explanation:
because 23 is the largest number on the triangle so the angle opposite of that side would be C
You swam the length of the pond shown below. How far did you swim? If necessary, round your answer to the nearest foot.

Answers
Answer:
The answer is 25 feet.
Step-by-step explanation:
You have to apply Pythagoras Theorem :
\( {c}^{2} = {15}^{2} + {20}^{2} \)
\( {c}^{2} = 625\)
\(c = \sqrt{625} \)
\(c = 25 \: feet\)

Question 3 Let X1, X2,..., Xn be independent random variables, each having a uniform distri- bution over (0,1). Let M = maximum (X₁, X₂,..., Xn). Show that the distribution function of M, FM(-), is given by FM(x)=x, 0≤x≤1 What is the probability density function of M?
Answers
The distribution function of M, FM(-), is given by FM(x) = x, 0 ≤ x ≤ 1.
The probability density function of M is\(fM(x) = n * x^(^n^-^1^)\), 0 ≤ x ≤ 1.
In order to understand the distribution function of M, we need to consider the probability that M is less than or equal to a given value x. Since each Xi is uniformly distributed over (0,1), the probability that Xi is less than or equal to x is x.
For M to be less than or equal to x, all of the random variables Xi must be less than or equal to x. Since these variables are independent, their joint probability is the product of their individual probabilities. Therefore, the probability that M is less than or equal to x can be expressed as the product of n x's: P(M ≤ x) = x * x * ... * x = \(x^n\).
The distribution function FM(x) is defined as the probability that M is less than or equal to x. Therefore, FM(x) = P(M ≤ x) = \(x^n\).
To find the probability density function (PDF) of M, we differentiate the distribution function FM(x) with respect to x. Taking the derivative of \(x^n\)with respect to x gives us \(n * x^(^n^-^1^)\). Since the range of M is (0,1), the PDF is defined only within this range.
The distribution function of M is FM(x) = x, 0 ≤ x ≤ 1, and the probability density function of M is \(fM(x) = n * x^(^n^-^1^)\), 0 ≤ x ≤ 1.
Learn more about probability
brainly.com/question/32575884
#SPJ11
Which of the following expressions is equal to 2x^2+8
Answers
Step-by-step explanation:
its a photo hope this will help you

how to write 1/400 as a percent
Answers
Answer:
0.25%
Step-by-step explanation:
Answer:
0.25%
Step-by-step explanation: you`re welcome :)
A movie theater charges $8.50 for an adult ticket to an evening showing of a popular movie. To help the local animal shelter, the theater management has agreed to reduce the price of each adult ticket by $0.50 for every can of pet food a customer contributes to a collection barrel in the theater lobby. Which of the following shows both an equation in which y represents the cost of an adult ticket in dollars for a customer who contributes x cans of pet food, and the graph of the cost if a customer brings in 2, 5, 8, or 10 cans of pet food?
A. y=8.5-0.50x
B. y=9x-0.5
C. y=8.5+0.50x
D. y=-9x-0.5
Answers
Answer:
Step-by-step explanation:
The answer is d
how many ways are there to distribute five distinguishable objects into three indistinguishable boxes?
Answers
There are 41 ways to distribute five distinguishable objects into three indistinguishable boxes.
The boxes are indistinguishable, there are 5 different ways to arrange the number of balls in each box: (5,0,0), (4,1,0), (3,2,0), (3,1,1), or (2,2,1).
There is 1 way to put all 5 balls in one box i.e (5,0,0)
(4,1,0): There are 5 choices for the 4 balls in one of the boxes.
(3,2,0): There are 10 choices for the 3 balls in the boxes.
(3,1,1): There are 10 choices for the 3 balls in one of the boxes, and we can simply split the last two among the other indistinguishable boxes.
(2,2,1): There are 10 options for one of the boxes with two balls, then 3 options for the second box with two balls, and one for remaining for the third.
Therefore the boxes with two balls are indistinguishable, we are counting each pair of balls twice so we have to divide by two.
So there are (10×3)/2=15 arrangements of balls as (2,2,1).
Hence the total number of arrangements for 3 indistinguishable boxes and 5 distinguishable balls is 1+5+10+10+15=41.
To know more about distinguishable and indistinguishable:
https://brainly.com/question/28353849
#SPJ4
Determined three ways have a total cost of six dollars each apple cost $1.50 each banana cost $.30 and there’s two more bananas then apples.
Answers
The cost of the apples is 2.9 dollars.
The cost of the bananas is 5.7 dollars.
How to find the number of fruits bought?The total cost is 6 dollars, each apple cost $1.50 each banana cost $.30 and there’s two more bananas then apples.
Therefore,
let
x = number of apples
y = 2x
where
y = number of bananasTherefore, using equations,
1.5(x) + y(0.30) = 6
Hence,
where
y = 2x
1.5(x) + 2x(0.30) = 6
1.5x + 0.6x = 6
2.1x = 6
divide both sides by 2.1
x = 6 / 2.1
x = 2.9 dollars
y = 2(2.9) = 5.7 dollars
learn more on cost here: https://brainly.com/question/31245217
#SPJ1
1.) Keisha's kitchen is shaped like a square. The room has an area of 256 feet squared. Which is the length of one side of Keisha's kitchen?
Also the attachment, and is it rational or irrational?

Answers
Answer:
1. 16 ft
\(\sf 2.\quad \dfrac{29}{99}\)
Step-by-step explanation:
Question 1Formula
Area of a square = s² (where s is the side length)
Given:
Area = 256 ft²Substitute the given area into the formula and solve for s:
\(\sf \implies 256=s^2\)
\(\sf \implies \sqrt{256}=\sqrt{s^2}\)
\(\sf \implies s=\pm 16\)
As distance is positive, the length of one side of Keisha's kitchen is 16 ft.
Question 2Converting a recurring decimal to a fraction
Let x equal the recurring decimal:
\(\implies \sf x=0.292929...\)
Create another number with recurring 29s by multiplying the above by 100:
\(\implies \sf 100x=29.292929...\)
To solve these two equations and write x as a fraction, subtract the first equation from the second to remove all the recurring digits after the decimal point:
\(\begin{array}{r r c l}& \sf 100x &= &\sf 29.292929...\\- & \sf x&=& \sf \phantom{..}0.292929...\\\cline{1-4} & \sf 99x&=& \sf29\\\cline{1-4}\end{array}\)
Therefore:
\(\implies \sf 99x=29\)
\(\implies \sf x=\dfrac{29}{99}\)
Therefore:
\(\sf \implies 0.\overline{29}=\dfrac{29}{99}\)
Learn more about converting recurring decimals to fractions here:
https://brainly.com/question/27788661
https://brainly.com/question/27643441
The density function of coded measurement for the pitch diameter of threads of a fitting is given below. Find the expected value of X. f(x) = {6/ √3 phi(1+x²) 0 < x < 1, otherwise
Answers
The density function for the pitch diameter of threads of a fitting is provided as f(x) = (6/√3) * φ(1+x²) for 0 < x < 1, and otherwise undefined. We need to calculate the expected value of X.
In probability theory, the expected value of a random variable represents the average value that we would expect to obtain from repeated measurements. To calculate the expected value of X in this case, we need to integrate the density function f(x) over the range of X and multiply by X.
Given the density function f(x) = (6/√3) * φ(1+x²), where φ denotes the standard normal distribution function, we want to find E(X), the expected value of X. Since the density function is defined only for 0 < x < 1, we will integrate over this range.
Using the definition of expected value, E(X) = ∫(x * f(x)) dx, we can substitute the density function and limits to obtain:
E(X) = ∫[0,1] (x * (6/√3) * φ(1+x²)) dx.
To evaluate this integral, we would need a specific expression for the standard normal distribution function φ(x). Without that information, we cannot calculate the expected value precisely.
In conclusion, to find the expected value of X for the given density function, we would require further details or an expression for the standard normal distribution function φ(x).
Learn more about average here: https://brainly.com/question/8501033
#SPJ11
I need help please!
Ap calculus

Answers
9514 1404 393
Answer:
(b) -15
Step-by-step explanation:
The area under the curve from -5 to +5 can be divided into two trapezoids. The one from x=-5 to x=1 has an area of ...
A = 1/2(b1 +b2)h = 1/2(1 +6)(5) = 17.5
The one from x=1 to x=5 has an area of ...
A = 1/2(4 +3)(-1) = -3.5
So, the total area from x=-5 to x=+5 is 17.5 -3.5 = 14. This is the amount by which f(x) increases from f(-5) to f(5). That is ...
f(-5) +14 = -1
f(-5) = -15

mr. ng can complete a job in x hours while mr. luciano can complete the same job in y hours. how much of the job can they complete if they work together for k hours?
Answers
They can complete k(1/x + 1/y) portion of the job if they work together for k hours.
We have,
If Mr. Ng can complete a job in x hours and Mr. Luciano can complete the same job in y hours, their individual rates of work are given by 1/x and 1/y, respectively.
Working together, their combined rate of work is the sum of their individual rates, which is 1/x + 1/y.
If they work together for k hours, the amount of the job they can complete is given by the product of their combined rate and the time they work, which is k(1/x + 1/y).
Thus,
They can complete k(1/x + 1/y) portion of the job if they work together for k hours.
Learn more about time and work here:
https://brainly.com/question/19382734
#SPJ12
he minute hand on a watch is 6 mm long and the hour hand is 5 mm long. how fast is the distance between the tips of the hands changing at one o'clock? (round your answer to one decimal place.)
Answers
The rate at which the distance between the tips of the hands are changing at one o'clock is 16.3 mm/h
What is the rate of change of a function?The rate of change of a function is the rate at which the output variable changes with respect to the input variable.
Let m represent the minute hand, let h represent the hour hand, and let s represent the distance between the minute hand and the hour hand, we get
s² = m² + h² - 2·m·h·cos(S)
The angle, ∠S = 2·π/(12) = π/6
Therefore;
s² = 6² + 5² - 2×6×5×cos(π/6) = 61 + 60·(√3/2)
s = √(61 + 60·(√3/2))
s² = m² + h² - 2·m·h·cos(S)
\(\dfrac{d}{dt} (s^2)= \dfrac{d}{dt} \left(m^2+ h^2-2\cdot m \cdot h\cdot cos(\theta)\right)\)
\(\dfrac{d}{dt} (s^2)= 2\cdot s\cdot \dfrac{ds}{dt}= -2\cdot m \cdot h\times (-sin(\theta)\right))\dfrac{d\theta}{dt}\)
Which indicates that we have;
\(2\cdot s\cdot \dfrac{ds}{dt}= -2\cdot m \cdot h\times (-sin(\theta)\right))\dfrac{d\theta}{dt}\)
\(\dfrac{ds}{dt}=\dfrac{ -2\cdot m \cdot h\times \left(-sin(\theta)\right))\dfrac{d\theta}{dt}} {2\cdot s}\)
\(\dfrac{d\theta}{dt}=-\dfrac{11\cdot \pi}{6}\)
Therefore;
\(\dfrac{ds}{dt}=\dfrac{ -2\cdot m \cdot h\times \left(-sin(\theta)\right))\dfrac{d\theta}{dt}} {2\cdot s}\)
\(\dfrac{ds}{dt}=\dfrac{ 2\times 6 \times 5 \times 0.5)\dfrac{-11\cdot \pi }{6}} {2\times \sqrt{61 + 60\times \dfrac{\sqrt{3}}{2}} } \approx -16.3\)
The rate at which the hour hand is changing is approximately 16.3 mm/h
Learn more about the rate of change of a function here:
https://brainly.com/question/10611843
#SPJ1
Pala says that she can draw an array with a total of 17 counters placed in 3 rows is she correct? if she is draw the array. if she is not, explain why not.
Answers
She cannot draw an array of 17 counters with three rows.
How to determine the true statement?The given parameters are:
Counter = 17
Rows = 3
An array is represented as:
Array = Rows * Columns
Where Rows and Columns are integers greater than 0
So, we have
3 * Column = 17
Divide by 3
Column = 5.667
Recall that Rows and Columns are integers greater than 0
This means that she cannot draw an array of 17 counters with three rows.
Read more about arrays at:
https://brainly.com/question/16266708
#SPJ4
(1 point) a rectangular swimming pool is 8 ft deep, 20 ft wide and 20 ft long. if the pool is filled to 1 ft below the top, how much work is required to pump all the water into a drain at the top edge of the pool? (use 62.4 lb/ft2 for the weight density of water.)
Answers
This gives us a total of 1,583,616 ft-lbs of work required to pump the water out of the pool.
What is amount?Amount is a numerical value that refers to the total sum of money or other type of payment due. It is used to quantify the size of a transaction, the cost of goods or services, or any other type of financial transaction. Amounts can be expressed in a variety of different currencies, and they can be negative (owing) or positive (owed).
To calculate the amount of work required to pump all the water from the rectangular swimming pool into a drain at the top edge, we must first calculate the volume of the water in the pool. Volume is calculated by multiplying the length, width, and depth of the pool, which in this case is 20 ft x 20 ft x 8 ft = 3,200 cubic ft. Since the pool is filled to 1 ft below the top, the volume of water is 3,200 ft3 - 20 ft3 = 3,180 ft3.
Next, we must calculate the weight of the water, which is the volume multiplied by the weight density of water (62.4 lb/ft3). The weight of the water in the pool is 3,180 ft3 x 62.4 lb/ft3 = 197,952 lbs.
Finally, to calculate the amount of work required to pump the water from the pool into a drain at the top edge, we must multiply the weight of the water (197,952 lbs) by the height of the drain (8 ft). This gives us a total of 1,583,616 ft-lbs of work required to pump the water out of the pool.
To know more about amount click-
https://brainly.com/question/24795637
#SPJ1
solve the simultaneous equations
y = 2 - x
6x + 5y = 11
x + 2y = 2
2x + y = 1
Answers
Answer:
x = 2
y = 0
Step-by-step explanation:
Here are the simultaneous equations:
\(y=2-x\\6x+5y=11\\x+2y=2\\2x+y=1\\\)
There are only two unknown values, so only two equations are needed to find the answer. I will use these:
\(y=2-x\\x+2y=2\)
Substitute the first equation into the y in the second equation:
\(x+2(2-x)=2\)
Simplify
\(x+4-2x=2\\x=2\)
Use the value of x to find y in equation 1:
\(y=2-x\\y=2-2\\y=0\)
(1 point) find the interval of convergence for the power series ∑n=2[infinity](x−5)n3n
Answers
The interval of convergence for the given power series is (2, 8).
To find the interval of convergence for the given power series. We have the power series:
∑(n=2 to ∞) ((x-5)ⁿ)/(3ⁿ)
To find the interval of convergence, we'll use the Ratio Test. For the Ratio Test, we need to compute the limit:
L = lim (n → ∞) |(a_(n+1)/a_n)|
For our series, a_n = ((x-5)ⁿ)/(3ⁿ). Therefore, a_(n+1) = ((x-5)(n+1))/(3(n+1)). Now, let's compute the ratio:
|(a_(n+1)/a_n)| = |(((x-5)(n+1))/(3(n+1))) / (((x-5)ⁿ)/(3ⁿ))|
Simplify the expression:
|(a_(n+1)/a_n)| = |(x-5)/3|
The series converges if L < 1. So we have:
|(x-5)/3| < 1
Now, we'll solve for x to find the interval of convergence:
-1 < (x-5)/3 < 1
Multiply each term by 3:
-3 < x-5 < 3
Add 5 to each term:
2 < x < 8
You can learn more about convergence at: brainly.com/question/14394994
#SPJ11
Will give brainliest!
What is the slope of the line passing through the points (0, −5) and (4, 2)?
Answers
Which translation are performed on f(x) = ln(x) to graph g(x) = –ln(x + 3) – 3?
a. to the left 3?
b. to the right 3?
c. up 3
d. down 3
please right answers only.
Answers
The translations performed are
a. to the left 3d. down 3How to describe the transformation from the parent function?From the question, we have the following function that can be used in our computation:
f(x) = ln(x)
g(x) = -ln(x + 1) - 3
First, we have the transformation to be:
From f(x) = ln(x) to f(x) = -ln(x)
This means a reflection across the x-axis
Next, we have
From f(x) = -ln(x) to f(x) = -ln(x + 3)
This means the function is translated left by 3 units
Next, we have:
From f(x) = -ln(x + 3) to f(x) = -ln(x + 3) - 3
This means the function is translated down by 3 units
Hence, the translation is 3 units left and 3 units down
Read more about transformation at
brainly.com/question/27224272
#SPJ1
Please help, will give brainliest to most educated answer.


Answers
2 . I’m not so sure about this question sorry
find the general solution of the given differential equation. (x + 1) dy dx + (x + 2)y = 2xe−x
Answers
The general solution of the given differential equation (x + 1) dy/dx + (x + 2)y = 2\(xe^{-x}\) is y = \(Cx^{-x}\) + x - 2, where C is a constant.
In order to find the general solution, we can rearrange the equation by dividing both sides by (x + 1):
dy/dx + (x + 2)/(x + 1)y = 2\(xe^{-x}\)/(x + 1).
Next, we notice that the left-hand side can be rewritten as the derivative of y with respect to x times a function of x. This suggests that the equation can be solved using an integrating factor. The integrating factor is given by the exponential of the integral of (x + 2)/(x + 1) with respect to x:
IF = e^{(∫(x + 2)/(x + 1) dx) } = \(e^{x+2}\)ln|x + 1|.
multiplying both sides of the equation by the integrating factor, we obtain:
\(e^{x+2}\)ln|x + 1|dy/dx + (x + 2)\(e^{x+2}\)ln|x + 1|y = 2xe^(-x)\(e^{x+2}\)n|x + 1|.
Simplifying the equation further, we have:
d/dx (\(e^{x+2}\)ln|x + 1|y) = 2xln|x + 1|.
Integrating both sides with respect to x, we get:
\(e^{x+2}\)ln|x + 1|y = x^2ln|x + 1| + C,
where C is the constant of integration. Finally, solving for y, we obtain the general solution:
y = (\(x^{2}\)ln|x + 1| + C)/(\(e^{x+2}\)ln|x + 1|) = Ce^(-x) + x - 2,
learn more about integration here:
https://brainly.com/question/31744185
#SPJ11
4−(−8)= please help i need it now
Answers
Answer:
Step-by-step explanation:
What is the GCF for 282, 540, and 28
Answers
Sun valley and Madison are 6cm apart on a map that has a scale of 1cm: 7km how far apart are the real cities
Answers
Answer:
42 km apart
Step-by-step explanation:
1 cm : 7km scale
6 cm apart on map means 6*7km.
6*7 = 42km apart.
Ten people (labeled 1-10) have purchased raffle tickets for a fundraiser. However, they did not all purchase the same
number of tickets. One ticket is to be selected at random. Which of the following could be the probability distribution for
the winning ticket?
C
1
0.10
1
2
0.01 0.01
2
0.10
1
3
4
5
6
0.10 0.10 0.10 0.10
3
4
5
0.05 0.07 0.68
1
2
0.125 0.125
6
0.01
2 3
4
5
6
7 8 9 10
0.01 0.11 0.02 0.12 0.03 0.13 0.04 0.14 0.05 0.15
3
0.125
7
8 9 10
0.10 0.10 0.10 0.10
5
7 8 9 10
0.05
0.03 0.01 0.08
6
4
7
9
10
0.125 0.125 0.125 0.125 0.125 0.125 0.125
8

Answers
The correct option is A: the probability distribution for the winning ticket:
1 2 3 4 5 6 7 8 9 10
0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10
Explain about the probability distribution?A frequency distribution that has been idealised is a probability distribution.
Each individual sample or dataset is described by its frequency distribution. It's the number of times in the dataset that each possible value for a particular variable appears.The probability of occurrence of a value determines how frequently it appears in a sample. Probability is a value between 0 and 1 that indicates the likelihood that something will happen:Zero denotes impossibility.1 denotes a certainty.Total people = 10 (1 - 10)
One ticket is selected at random from each person.
As the selection is independent events of each other, each will have the same probability.
So,
probability = favourable outcome / total outcome.
probability = 1/10
probability = 0.10.
Thus, the correct option is A: the probability distribution for the winning ticket:
1 2 3 4 5 6 7 8 9 10
0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10 0.10
Know more about the probability distribution
https://brainly.com/question/24756209
#SPJ1
A parking garage charges a fixed amount of money for each hour that it is used.
Answers
Solve each matrix equation
[3 2 -1 5] X = [-10 -11 26 -36]
Answers
The solution to the matrix equation [3 2 -1 5] X = [-10 -11 26 -36] is X = [-150/17 -53/17 92/17 -182/17].To solve the matrix equation [3 2 -1 5] X = [-10 -11 26 -36], you need to find the value of matrix X.
Here are the steps to solve the equation:
Step 1: Write the matrix equation in the form AX = B, where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.
[3 2 -1 5] X = [-10 -11 26 -36]
Step 2: To isolate X, multiply both sides of the equation by the inverse of matrix A.
A^(-1) [3 2 -1 5] X = A^(-1) [-10 -11 26 -36]
Step 3: The inverse of matrix A can be found by using the formula (1/det(A)) * adj(A), where det(A) is the determinant of matrix A and adj(A) is the adjugate of matrix A.
Step 4: Calculate the determinant of matrix A.
det(A) = (3 * 5) - (2 * -1) = 15 + 2 = 17
Step 5: Calculate the adjugate of matrix A.
adj(A) = [5 -1; 2 3]
Step 6: Calculate the inverse of matrix A using the formula (1/det(A)) * adj(A).
A^(-1) = (1/17) * [5 -1; 2 3] = [5/17 -1/17; 2/17 3/17]
Step 7: Multiply both sides of the equation by A^(-1) to isolate X.
[5/17 -1/17; 2/17 3/17] [3 2 -1 5] X = [5/17 -1/17; 2/17 3/17] [-10 -11 26 -36]
Step 8: Simplify the equation.
[1 0 0 0; 0 1 0 0] X = [-150/17 -53/17 92/17 -182/17]
Step 9: The value of X is the right-hand side of the equation.
X = [-150/17 -53/17 92/17 -182/17]
Therefore, the solution to the matrix equation [3 2 -1 5] X = [-10 -11 26 -36] is X = [-150/17 -53/17 92/17 -182/17].
learn more about matrix equation on :
https://brainly.com/question/11989522
#SPJ11
using equation 0.3, what can be plotted to obtain a straight-line relationship from which the value of k can be obtained? support your answer by explicitly showing how k relates to the resulting parameters of the line fit
Answers
Using equation 0.3, to obtain a straight-line relationship from which the value of k can be determined, you can plot the natural logarithm (ln) of the content loaded against time. By doing this, you will get a linear graph where the slope represents the rate constant (k).
Equation 0.3 refers to the exponential decay equation, which can be used to model a process in which a quantity decreases exponentially over time. To obtain a straight-line relationship from this equation, we can take the natural logarithm of both sides:
ln(y) = ln(y0) - kt
where y is the quantity at time t, y0 is the initial quantity, k is the decay constant, and ln denotes the natural logarithm. If we plot ln(y) versus t, we will obtain a straight line with slope -k and y-intercept ln(y0).
To obtain the value of k from this line fit, we can use the slope formula:
k = -slope
Therefore, the value of k is simply the negative of the slope of the line fit. This means that the larger the slope (i.e. the steeper the line), the faster the decay process. Conversely, a smaller slope indicates a slower decay process.
In summary, if we have content loaded using equation 0.3, we can plot ln(y) versus t to obtain a straight-line relationship from which the value of k can be obtained. The value of k is related to the resulting parameters of the line fit through the slope of the line, which is simply the negative of k.
To know more about equations visit:
https://brainly.com/question/29538993
#SPJ11