Answers
Answer:
B) A and C
Step-by-step explanation:
A and C are negative reciprocals of each other.
Because I had the same question and got it right
Related Questions
Henry and five friends are going to the movies. Tickets cost $8 each. Henry used this model to help him find the total cost of the tickets. Which shows one way to break apart the array to find the product?
Answers
Answer:
(7 x 5) + (7 X 3) = 7 X 8 or (7 x 4) + (7 X 4) = 7 X 8
Step-by-step explanation:
I think your question is missed of key information, allow me to add in and hope it will fit the original one.
Please have a look at the attached photo.
My answer:
The total number of people: 7 Ticker costs: $8 each=> the total cost = the total number of people * the ticket cost each
= 7 X 8
Hence, he can use this way to break apart the array to find the product:
(7 x 5) + (7 X 3) = 7 X 8 or (7 x 4) + (7 X 4) = 7 X 8
Hope it will find you well.

{4x-y=5
{x+y=5
HELP PLEASE!!!
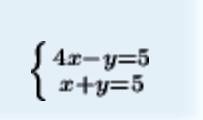
Answers
Answer:
(2, 3 )
Step-by-step explanation:
4x - y = 5 → (1)
x + y = 5 ( subtract y from both sides )
x = 5 - y → (2)
substitute x = 5 - y into (1)
4(5 - y) - y = 5
20 - 4y - y = 5
20 - 5y = 5 ( subtract 20 from both sides )
- 5y = - 15 ( divide both sides by - 5 )
y = 3
substitute y = 3 into (2)
x = 5 - y = 5 - 3 = 2
solution is (2, 3 )
Step-by-step explanation:
the easiest way to solve such a system of 2 equations is very often to multiply one equating by a certain constant and then add both equations, so that one variable is eliminated.
in our case we don't need to multiply with anything. we can simply add :
4x - y = 5
x + y = 5
-----------------
5x 0 = 10
x = 10/5 = 2
x + y = 5
2 + y = 5
y = 5 - 2 = 3
so, our solution is
x = 2
y = 3
the diameter of a cone is 1.5 meters, the height is 1.5 times the radius, what is the volume?
Answers
Answer:
.66 cu. meters
Step-by-step explanation:
volume for cone is V=1/3 x TT x r^2 x height
TT (pi) is 3.14
radius is 1/2 of diameter (1/2 x 1.5 = .75 )
height is 1.5 x radius (1.5 x .75 = 1.125)
V= 1/3 x 3.14 x .75^2 x 1.125
V= .66 cu. meters
Question
The volume of a cube is 0.125 in^3 What is the length of one side?

Answers
Answer:
0.5 inches
Step-by-step explanation:
Volume of a cube = L × L × L = L³
0.125 = L³
L = ³√0.125
L = 0.5 inches
Find the local maximum and local minimum values of f using both the First and Second Derivative Tests. f(x) = 3 + 6x2 - 4x3 = local maximum value x local minimum value x
Answers
To find the local maximum and local minimum values of the function f(x) = 3 + 6\(x^2\) - 4\(x^3\), we can use the First and Second Derivative Tests.
The critical points of the function can be determined by finding where the first derivative is equal to zero or undefined. Then, by analyzing the sign of the second derivative at these critical points, we can classify them as local maximum or local minimum points.
To find the critical points, we first calculate the first derivative of f(x) as f'(x) = 12x - 12\(x^2\). Setting this derivative equal to zero, we solve the equation 12x - 12\(x^2\) = 0. Factoring out 12x, we get 12x(1 - x) = 0. So, the critical points occur at x = 0 and x = 1.
Next, we find the second derivative of f(x) as f''(x) = 12 - 24x. Evaluating the second derivative at the critical points, we have f''(0) = 12 and f''(1) = -12.
By the First Derivative Test, we can determine that at x = 0, the function changes from decreasing to increasing, indicating a local minimum point. Similarly, at x = 1, the function changes from increasing to decreasing, indicating a local maximum point.
Therefore, the local minimum occurs at x = 0, and the local maximum occurs at x = 1 for the function f(x) = 3 + 6\(x^2\) - 4\(x^3\).
Learn more about derivative here:
https://brainly.com/question/29144258
#SPJ11
Rory records the percentage of battery life remaining on his phone throughout a day. The graph represents the percentage of battery life remaining after a certain number of hours. A graph titled Phone Battery Life. The horizontal axis shows Elapsed Time (hours) numbered 2 to 20, and the horizontal axis shows Battery Life (%) numbered 10 to 120. A line begins at 100% in 0 hours, to 20% in 8 hours, to 100% from 10 to 12 hours, to 60% in 16 hours, to 100% from 17 to 20 hours. At which times could Rory's phone have been plugged into the charger? Select three options. 6 hours 9 hours 11 hours 14 hours 19 hours
Answers
Answer:
9,11,19
Step-by-step explanation:
let x be the hours and y the percentage
x=0 , y=100
x=8 , y=80
x=9 , y=0
x=10 , y=100 , x=11 still charging so it is still plugged in
x=16 , y=60 and so on ....
x=18 , y=20
and it will charged again
the answer is 9,11,19
True or False?
Every rectangle with four congruent sides is a square.
Every rhombus is a quadrilateral.
Every square is a parallelogram.
Every quadrilateral is a square.
Answers
Every rectangle with four congruent sides is a square -> True
Every rhombus is a quadrilateral -> True
Every square is a parallelogram -> True
Every quadrilateral is a square -> False.
What is a square?A square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle with two equal-length adjacent sides.
here, we have,
we know that,
Every rectangle with four congruent sides is a square -> True
Every rhombus is a quadrilateral -> True
Every square is a parallelogram -> True
Every quadrilateral is a square -> False.
To learn more on Square click :
brainly.com/question/14198272
#SPJ1
4) Find x if m/2 = 18x - 1 and
m2UWV = 33x + 1.
W
U
Answers
For given expression x will be equal to 1.
What are expressions?
Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between. The mathematical operators can be of addition, subtraction, multiplication, or division. For example, x + y is an expression, where x and y are terms having an addition operator in between. In math, there are two types of expressions, numerical expressions - that contain only numbers; and algebraic expressions- that contain both numbers and variables.
e.g. A number is 6 more than half the other number, and the other number is x. This statement is written as x/2 + 6 in a mathematical expression. Mathematical expressions are used to solve complicated puzzles.
Now,
Given expression is m/2=18x-1
where m=33x+1
By putting value of m
33x+1=(18x-1)*2
33x+1=36x-2
3x=3
x=1
Hence,
For given expression x will be equal to 1.
To know more about expressions visit the link
https://brainly.com/question/13947055?referrer=searchResults
#SPJ1
Question 4 of 10
You have $10.00 and want to buy all of the items below. How much change
will you have left after you make your purchase? Do not include $ in your
answer.
COST
ITEM
Pancake Mix
Eggs
Syrup
$2.18
$2.28
$3.98
PLS HELP!’
Answers
Answer: 1.56
Step-by-step explanation:
Add all the cost together, the subtract the ten dollars.
2.18 + 2.28+ 3.98 = 8.44
10.00 - 8.44 = 1.56
Find an equation for the line that passes through the points (-6,6)and (4,6).
Answers
To find the equation of the line, we will use the formula below;
\(y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\)x₁=-6 y₁=6 x₂=4 y₂=6
substitute the values into the formula
\(y\text{ - 6 =}\frac{6-6}{4+6}(x\text{ + 6)}\)\(y-6=\frac{0}{10}(x+6_{})\)
y - 6 = 0
y = 6
√x =a solve for x
please help I need the answer ASAP.
Answers
Answer: 2
Step-by-step explanation:
Answer:
x = a²
Step-by-step explanation:
To undo the square root, you have to square both sides of the equation so it becomes...
(√x )² = a²
That undoes the square soot so it is
x = a²
5 times what equals 53
Answers
Answer:
The answer is 10.6
Step-by-step explanation:
Divide 53 by 5 :)
Answer:
10.6
Step-by-step explanation:
53/5=10.6
or 10.6 multiplied by 5 equals 53
Can somebody help me with this question

Answers
Answer:
900°
Step-by-step explanation:
The interior angles sum = 180° ( n - 2 )
~~~~~~~~
n = 7
180° ( 7 - 2 ) = 900°
Answer:
900 degrees
Step-by-step explanation:
just apply the formulas discussed in class !
The sum of interior angles in a triangle is 180°. To find the sum of interior angles of a polygon, multiply the number of triangles in the polygon by 180°.
The number of triangles in each polygon is two less than the number of sides.
The formula for calculating the sum of interior angles is:
(n−2)×180∘ (where n is the number of sides)
in our case we have 7 sides.
so, we could split this polygon into 5 triangles.
each of these triangles would have an angle sum of 180°.
so, the angle sum of the polygon is
5×180 = 900°
1)The equation y=−4.9x2+8.82x+1.96 represents the height of the trajectory of a ball x seconds after it was released. The solutions to 0=−4.9x2+8.82x+1.96 are x=−0.2 and x=2. Which of these solutions represents the time it takes the ball to hit the ground?(1 point)
a) both x=−0.2 and x=2
b) x=−0.2
c) x=2
d) Neither of the solutions represents the correct time.
2) The equation y=−4.9x^2+19.5x+1.75 represents the height of the trajectory of a ball x seconds after it was released. At what time is the ball 10 meters above the ground?(1 point)
a) The ball never is never 10 meters above the ground.
b) approximately 0.5 seconds and 3.5 seconds
c) approximately 3.5 seconds
d) approximately 0.5 seconds
A baseball player throws a baseball directly upward into the air. The height of the ball is given by the equation y=−4.9x^2+89.5x+1.75 where y is the height in meters and x is the time in seconds. Is this equation a reasonable model for the ball's trajectory? Explain(1 point)
a) No, the initial height is 1.75 meters, which is much taller than any person.
b) No, the equation does not match the model for projectile motion.
c) No, the initial velocity would be 89.5 meters per second. This is approximately 200 miles per hour, which is faster than any human can throw a baseball.
d) Yes, the equation matches the model for projectile motion, so it is a reasonable model for the ball's trajectory.
The equation y=−16x2+275 models the height of a projectile where y is the height in meters and x is the time in seconds. Which of the following situations is the real-world scenario that is best modeled by the given equation?(1 point)
a) A ball being dropped from shoulder height.
b) A child tossing a ball into the air.
c) A stone being dropped off of the edge of a cliff.
d) A tennis ball being launched into the air by a tennis racket.
Answers
Answer:
Number 1 is A
Step-by-step explanation:
what is the sum of the perimeter in units of the five squares in the design
Answers
Answer:
Assuming that the squares are the same size,
the sum of the perimeter of the five squares =
(20 units × side length of each square in units)
If the squares are different sizes, the sum of the perimeter of the five squares =
(4 units × side length of square 1 in units) + (4 units × side length of square 2 in units) + (4 units × side length of square 3 in units) + (4 units × side length of square 4 units) + (4 units × side length of square 5 in units)
Explanation:
The perimeter of a square is 4 × side length because a square has 4 sides and the perimeter of a figure is the surrounding length of the figure.
A jeweler designs necklaces that are perfectly round open- circles each with a radius of 8.4mm. (1m= 1000mm) What is the largest number of open- circle necklaces that can be made from a wheel of spooled gold that is 42m long?
Answers
Answer:
795
Step-by-step explanation:
First, we find the circumference of 1 ring.
c = 2πr
c = 2 × 3.14159 × 8.4 mm
c = 52.7787 mm
The circumference of 1 ring is the length of spooled gold used for 1 ring.
The spool has a total length of 42 m.
42 m × 1000 mm / 1 m = 42,000 mm
The spool has a total length of 42,000 mm.
Now we divide the length of the spool by the length of 1 ring.
42,000 mm / 52.7787 mm = 795.78
He can make 795 rings.
Solve for a: a - 17 = -10
Answers
Answer:
a = 7
Step-by-step explanation:
a - 17 = -10
Add 17 to each side
a - 17+17 = -10+17
a = 7
Answer:
a = 7
Step-by-step explanation:
Add 17 to each side, so it cancels out the -17. It should now looks like this: a = 7I hope this helps!
over a 24-hour period, brown bears counted 940 salmon swimming upstream, and they safely assumed that they only counted 20% of the total number of fish going by. the salmon-spawning haven along copper river measures approximately 70,000 cubic meters of water. given that the haven was empty before this week, that the salmon swim upstream at a constant rate, and that once they reach the haven, the salmon hang out there indefinitely, what will the population density of salmon in the copper river spawning haven be after one week (to the nearest thousandth fish per cubic meter)?
Answers
The population density of salmon in the Copper River spawning haven after one week is approximately 0.218 fish/m3.
We can calculate the population density of salmon in the spawning haven by dividing the total number of salmon by the volume of the haven:
Population density = total number of salmon / volume of haven
Population density = 19,600 / 90,000
Population density = 0.2178 fish/m3
Rounding to the nearest thousandth of fish/m3 gives us a population density of 0.218 fish/m3.
Density is a physical property of matter that measures the amount of mass per unit volume of a substance. Density is an important concept in the physical sciences and is a fundamental property of matter that can provide valuable information about the nature of a substance.
The density of an object can provide information about its composition and physical properties. For example, materials with a higher density are generally more compact and have a greater mass per unit volume than materials with a lower density. This property is important in many scientific fields, including physics, chemistry, and engineering. Density can also be used to determine if an object will float or sink in a fluid.
To learn more about Density visit here:
brainly.com/question/29775886
#SPJ4
determine the area of the given region under the curve. y = 1/x6
Answers
The area of the region under the curve y = 1/x^6 between x = 1 and x = ∞ is 1/5 square units.
The region under the curve y = 1/x^6 is bounded by the x-axis and the vertical line x = 1. To find the area of this region, we need to evaluate the definite integral ∫[1,∞] 1/x^6 dx.
We can do this using the power rule of integration:
∫[1,∞] 1/x^6 dx = [-1/5x^5] [1,∞] = [-1/(5∞^5)] - [-1/(5(1)^5)] = 1/5
Therefore, the area of the region under the curve y = 1/x^6 between x = 1 and x = ∞ is 1/5 square units.
Learn more about area here
https://brainly.com/question/25292087
#SPJ11
problem 12a: fullerton iv company has had a policy of reordering inventory every 30 days. using the data below, what is the economic order quantity eoq?ordering cost f $10 per ordercarrying cost c 20% of purchase price purchase price p $10 per unittotal sales per year s 1,000 units safety stock days per year 360. continuing with the previous question, what is the total inventory cost, tic?
Answers
The economic order quantity (EOQ) for Fullerton IV Company is 100 units. The total inventory cost (TIC) is $200.
The economic order quantity (EOQ) for Fullerton IV Company can be calculated using the given information. The EOQ formula is:
EOQ = √((2 * S * F) / C)
where S is the total annual sales, F is the ordering cost per order, and C is the carrying cost as a percentage of the purchase price.
Given data:
Ordering cost (F) = $10 per order
Carrying cost (C) = 20% of purchase price
Purchase price (P) = $10 per unit
Total sales per year (S) = 1,000 units
Substituting these values into the formula, we get:
EOQ = √((2 * 1,000 * 10) / (0.2 * 10))
Simplifying further:
EOQ = √(20,000 / 2)
EOQ = √10,000
EOQ = 100
Therefore, the economic order quantity (EOQ) for Fullerton IV Company is 100 units.
To calculate the total inventory cost (TIC), we need to consider both the ordering cost and the carrying cost. The formula for TIC is:
TIC = (S / EOQ) * F + (EOQ / 2) * C * P
where S is the total annual sales, EOQ is the economic order quantity, F is the ordering cost per order, C is the carrying cost as a percentage of the purchase price, and P is the purchase price per unit.
Substituting the given values into the formula, we have:
TIC = (1,000 / 100) * 10 + (100 / 2) * 0.2 * 10
Simplifying further:
TIC = 10 * 10 + 50 * 0.2 * 10
TIC = 100 + 100
TIC = 200
Therefore, the total inventory cost (TIC) for Fullerton IV Company is $200.
To know more about economic order quantity (EOQ), refer here:
https://brainly.com/question/9068415#
#SPJ11
Jalen earns `\$33` for babysitting `4` hours. At this rate, how much will he earn if he babysits for `7` hours?.
Answers
Answer:
Step-by-step explanation:
If 33/4 is 8.25 dollars, that means in 7 hours he will make on average 57.75 dollars if 8.25 times 7 is 57.75.
85. What is the value of x?والے1040)DDrawing not to scaleA 38°B. 128°C. 76D. 52°

Answers
Given:
One of the angle of a triangle is 104°.
The objective is to find the missing angle x.
If two sides of a triangle are equal, then it is an isosceles triangle.
In an isosceles triangle, the angle formed by the equal sides is also equal.
Then, the value of angle x can be calculated angle sum property of triangle.
\(\begin{gathered} x+x+104\degree=180\degree \\ 2x+104\degree=180\degree \\ 2x=180\degree-104\degree \\ 2x=76\degree \\ x=\frac{76}{2} \\ x=38\degree \end{gathered}\)Hence, option (A) is the correct answer.
What is x, the distance between points A and A'? 2.4 units 4.8 units 13.6 units 14.4 units
Answers
Answer: the answer is 13.6 units
Step-by-step explanation:
Answer:
C. 13.6 units
Step-by-step explanation:
i took the quiz on edge
Calculate the work done in lifting a 15-lb flower pot to a height of 4 ft above the ground.

Answers
Answer:
A. 60 ft·lb
Step-by-step explanation:
You want the work done lifting a 15-lb flower pot to a height of 4 ft.
WorkWork is the product of force and distance. When the pot is raised 4 ft, the work done is ...
W = F·d
W = (15 lb)(4 ft) = 60 ft·lb
<95141404393>
Please help i do not understand at all

Answers
The final graph should resemble a "V" shape starting from the origin and extending to the right (with two lines converging at the origin).
The given polynomial function f meets the criteria of being negative for all real numbers and having an increasing slope when x is less than -1 and between 0 and 1. Therefore, we can represent this graphically on the coordinate plane by starting at the origin (x=0, y=0). We can then plot a line going from the origin with a negative slope (moving left to right). This will represent the increasing slope of the graph when x<-1 and 0<x<1.
We can then plot a line going from the origin with a positive slope (moving left to right). This will represent the decreasing slope of the graph when -1<x<0 and x>1.
The final graph should resemble a "V" shape starting from the origin and extending to the right (with two lines converging at the origin). The graph should be entirely below the x-axis, since the given polynomial function is negative for all real numbers.
Therefore, the final graph should resemble a "V" shape starting from the origin and extending to the right (with two lines converging at the origin).
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1
Jackson digs a hole at a rate of 3/5 feet every 10 minutes. After digging for 40 minutes, Jackson places a plant in the hole that fills exactly 9/10 feet of the hole.
Relative to ground level, what is the elevation of the hole after placing the plant in the hole?
Enter your answer as a mixed number in the simplest form by filling in the boxes.
Answers
Given that Jackson digs a hole at a rate of 3/5 feet every 10 minutes, and he dug for 40 minutes. Thus, the total depth of the hole dug by him is given by:
3/5 x 4 = 12/5
= 2.4 feet (Depth of the hole dug by Jackson)
After he placed the plant in the hole, the depth of the plant is 9/10 feet.
So, the total depth of the hole that is filled after he placed the plant is:
2.4 + 9/10= 12/5 + 9/10
= 24/10 + 9/10
= 33/10 feet
Now, if we consider ground level as zero, then the elevation of the hole is 33/10 feet above the ground level.
Therefore, the relative elevation of the hole after placing the plant in the hole is 33/10 feet above ground level.
Jackson digs a hole at a rate of 3/5 feet every 10 minutes. After digging for 40 minutes, Jackson places a plant in the hole that fills exactly 9/10 feet of the hole. The problem is based on the concept of fraction addition and subtraction along with conversion of mixed fractions into improper fractions. Here, we need to calculate the elevation of the hole after the plant is placed. It is given that Jackson digs a hole at a rate of 3/5 feet every 10 minutes. After digging for 40 minutes, the total depth of the hole dug by Jackson is 2.4 feet. Now, when he places the plant in the hole that fills exactly 9/10 feet of the hole, the depth of the hole that is filled becomes 33/10 feet. Therefore, the relative elevation of the hole after placing the plant in the hole is 33/10 feet above ground level.
Relative elevation of the hole after placing the plant in the hole is 33/10 feet above ground level.
To know more about improper fractions visit:
brainly.com/question/29610823
#SPJ11
Determine the following probabilities a. For n-5 and π= 0.16, what is P(X:0)? b. For n 9 and x-0.50, what is P(X 8)? c. For n 9 and -0.40, what is P(X-7)? d. For n-6 and x-0.81, what is P(x-5)? a·When n 5 and x=0.16,PR=0)= Round to four decimal places as needed.) b. When n-9 and x -0.50, P(X 8) Round to four decimal places as needed.) c. When n-3 and π: 0 40, P(x-7)-[) Round to four decimal places as needed.) d. When n -6 and 0.81, P( 5) Round to four decimal places as needed)
Answers
P(X = 0) = 0.335 Probability = 0.335.The given formula for probability distribution is:P(X) = (n! / x! (n - x)!) * πx * (1 - π)n - xwhere, P = Probability X = Random variable, n = Total number of trialsπ = Probability of success. Let us consider the given probabilities:(a) For n - 5 and π = 0.16, what is P(X:0)?When n = 5 and x = 0, then n - x = 5.
Therefore,
P(X = 0) = (5! / 0! (5 - 0)!) * (0.16)0 * (1 - 0.16)5 - 0= (1 / 1) * 1 * 0.3277= 0.3277Round off the answer to four decimal places as needed.P(X = 0) = 0.3277.(b) For n 9 and x-0.50, what is P(X 8)?When n = 9 and x = 8, then n - x = 1. Therefore,P(X = 8) = (9! / 8! (9 - 8)!) * (0.50)8 * (1 - 0.50)9 - 8= (9 / 1) * 0.00390625 * 0.5= 0.0176.
Round off the answer to four decimal places as needed.P(X = 8) = 0.0176(c) For n 9 and -0.40, what is P(X-7)?When n = 9 and x = 7, then n - x = 2. Therefore,P(X = 7) = (9! / 7! (9 - 7)!) * (0.40)7 * (1 - 0.40)9 - 7= (36 / 1) * 0.0809856 * 0.027= 0.0807.
Round off the answer to four decimal places as needed.P(X = 7) = 0.0807(d) For n-6 and x-0.81, what is P(x-5)?When n = 6 and x = 5, then n - x = 1. Therefore,P(X = 5) = (6! / 5! (6 - 5)!) * (0.81)5 * (1 - 0.81)6 - 5= (6 / 1) * 0.3252718081 * 0.19= 0.3727Round off the answer to four decimal places as needed.P(X = 5) = 0.3727.
To determine the given probabilities, the probability distribution formula has been used. The formula used is:P(X) = (n! / x! (n - x)!) * πx * (1 - π)n - xWhere,P is the probability,X is the random variable,n is the total number of trials, andπ is the probability of success. The first probability is to calculate the probability for n - 5 and π = 0.16, what is P(X:0)?The value of x is zero, and n - x is 5. The formula is applied to get the probability, and it is rounded off to four decimal places as needed. The second probability is to calculate the probability for n 9 and x-0.50, what is P(X 8)?The value of x is 8, and n - x is 1. The formula is applied to get the probability, and it is rounded off to four decimal places as needed. The third probability is to calculate the probability for n 9 and -0.40, what is P(X-7)?The value of x is 7, and n - x is 2. The formula is applied to get the probability, and it is rounded off to four decimal places as needed. The fourth probability is to calculate the probability for n -6 and x-0.81, what is P(x-5)?The value of x is 5, and n - x is 1. The formula is applied to get the probability, and it is rounded off to four decimal places as needed.
Therefore, the probabilities for different values of n, x, and π have been calculated by using the probability distribution formula.
To know more about probability distribution :
brainly.com/question/29062095
#SPJ11
A hypothesis test was conducted to test whether has been an increase in the proportion of students that attend college right after high school. The resulting p-value from that test was .000548. Given an alpha level of .05, which of the following is TRUE?
A. There is no evidence to show an increase in the proportion of students attending college because the p-value is less than the alpha level, therefore we will fail to reject the null hypothesis.
B. There is evidence to show an increase in the proportion of students attending college because the p-value is less than the alpha level, therefore we will reject the null hypothesis.
C. There is evidence to show an increase in the proportion of students attending college because the p-value is less than the alpha level, therefore we will fail to reject the hypothesis.
D. There is no evidence to show an increase in the proportion of students attending college because the p-value is less than the alpha level, therefore we will reject the null hypothesis.
Answers
Answer:
D. There is no evidence to show an increase in the proportion of students attending college because the p-value is less than the alpha level, therefore we will reject the null hypothesis.
Step-by-step explanation:
Assuming a significance level of α=0.05, since 0.000548<0.05, we reject the null hypothesis and conclude that there is no evidence to show an increase in the proportion of students attending college. So option D is correct.
HELP ME PLEASE!!!
I will give brainlist to whoever helps me!!!!

Answers
Answer: t=15
Step-by-step explanation:
ST=9. BC=3
ST/BC=
9/3=3 ==> with this information, we can conclude that triangle ABC needs to be stretched by a scale factor of 3 in order to become triangle RST.
t=RS
RS=AB*3
RS=5*3
RS=15
t=15
General Sherman, a tree located in Sequoia National Park, stands 275
feet tall. To see the top of the tree, Carlos looks up at a 15° angle of elevation. If Carlos is 6 feet tall, how far is he from the base of the tree to the nearest foot? There are 4 options A.1004 B.1020 C.1026 D.1049
Answers
Answer:
Step-by-step explanation:
If Carlos is 6ft tall and looks up at the tree that is 275 ft tall, subtract those two.
275 - 6 = 269
Use tangent with the given angle and the new height. The distance is x.
tan15 = 269/x
x = 269/tan15
x = 1004ft
The distance from Carlos to the tree, given he is 6 feet tall and looks up at a 15° angle of elevation to see the top of a 275-foot tall tree located in Sequoia National Park, is 1026.
Hence option C is correct.
According to the information given,
We can set up a right triangle with Carlos's eye level, the top of the tree, And the base of the tree as the three points of the triangle.
Carlos's height of 6 feet can be used as one side of the triangle,
And we can use the tangent function to find the length of the adjacent side.
A tangent of 15 degrees is equal to the opposite side (height of the tree) divided by the adjacent side (distance from Carlos to the tree).
So, we can solve for the adjacent side by multiplying the height of the tree by the tangent of 15 degrees:
tan(15) = height of the tree / distance from Carlos to the tree
Distance from Carlos to the tree = height of the tree / tan(15)
Plugging in the values given:
Distance from Carlos to the tree = 275 / tan(15)
≈ 1026
Therefore,
The nearest foot to the distance from Carlos to the tree is option C. 1026.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ2
