Which is not a step in solving this problem?1/2^5A. Multiply 1 by 5.B. Change the operation,C. Multiply 5 by 2.D. Find the reciprocal of the divisor.
Answers
Given data:
The given question is:
\(\frac{1}{2}\text{ }\times\frac{1}{5}\)Now, first we will change the opeation instead of dividing one and a half by 5 we will write it as
\(\frac{1}{2}\times\frac{1}{5}\)Now we will multiply 5 by 2
\(\frac{1}{10}\)And then the answer is 0.1 which is the reciprocal of 10 (i.e. divisor in this case).
So, part A is not a step in solving this problem.
Related Questions
Find the polar coordinates of rectangular coordinates (-√2,1). Limit θ to the interval [0,2pi) and round 2 dceimal places if needed
Answers
The point (-√2,1) can also be represented as (√3, 5.18) in polar coordinates.
To find the polar coordinates of the rectangular coordinates (-√2,1), we can use the following formulas:
r = √(x² + y²)
θ = tan^⁻1(y/x)
Plugging in the given values of (-√2,1), we get:
r = √((-√2)² + 1²) = √(2 + 1) = √3
θ = tan^⁻1(1/(-√2)) ≈ 2.0344 radians
Note that since the point (-√2,1) is in the second quadrant, we need to add π to the value of θ obtained from the inverse tangent in order to obtain an angle in the interval [0,2π). Thus, we have:
θ ≈ 2.0344 + π ≈ 5.1779 radians
Rounding to 2 decimal places as needed, we get the polar coordinates of (-√2,1) as (r,θ) ≈ (√3, 5.18).
For such more questions on coordinate
https://brainly.com/question/29660530
#SPJ8
The next day Tamika records the temperature of 0°F at 8:00 a.m. and 1°F
at 10:00 a.m. Assume the temperature has been rising linearly since sunrise
at 6:00 a.m.
Use point-slope form to write a linear function to model the
situation. (Hint: Solve for y, then replace y with f(x)).
Answers
The equation of line in the point slope form is y = 2x + 8
What is an Equation of a line?
The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the equation be represented as A
Let temperature be denoted as x
Let the time be denoted as y
Let the initial temperature be = 0°F
Let the final temperature be = 1°F
Let the initial time be = 8 : 00 AM
Let the final time be = 10 :00 AM
And , the first point be P = P ( 0 , 8 )
The second point be Q = Q ( 1 , 10 )
Now , the slope of the equation is given as
Slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Substituting the values in the equation , we get
Slope m = ( 10 - 8 ) / ( 1 - 0 )
Slope m = 2
Now , the equation of line is given as y - y₁ = m ( x - x₁ )
Substituting the values in the equation , we get
y - 8 = 2 ( x - 0 )
y - 8 = 2x
Adding 8 on both sides of the equation , we get
y = 2x + 8
Therefore , the value of A is y = 2x + 8
Hence , the equation is y = 2x + 8
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ1
Calculate the amount you would pay (including tax) for an item normally priced at $329 on sale for 25% off where sales tax is 7.25%.
Answers
Answer: The amount you would pay (including tax) for an item normally priced at $329 on sale for 25% off where sales tax is 7.25% would be $264.63.
Step-by-step explanation: To calculate the final price including tax, we need to apply the discount first and then add the sales tax.
Discounted price = 0.75 x $329 = $246.75
Sales tax = 0.0725 x $246.75 = $17.88
Final price including tax = $246.75 + $17.88 = $264.63
Therefore, the amount you would pay (including tax) for an item normally priced at $329 on sale for 25% off where sales tax is 7.25% would be $264.63.
In a class of students, the following data
table summarizes how many students have a
cat or a dog. What is the probability that a
student chosen randomly from the class has
a cat?
Has a dog
Does not have a
dog
Has a cat
2
3
Does not have a
cat
12
10
Answers
The table can be summarized as follows:
| | Has a dog | Does not have a dog |
|----------|-----------|---------------------|
| Has a cat | 2 | 3 |
| Does not have a cat | 12 | 10 |
To find the probability that a student chosen randomly from the class has a cat, we need to find the total number of students who have a cat (regardless of whether or not they have a dog), and divide it by the total number of students in the class.
The number of students who have a cat is 2 (those who have a dog and a cat) + 3 (those who have a cat but do not have a dog) = 5.
The total number of students in the class is the sum of all four categories: 2 (has a cat and a dog) + 3 (has a cat, does not have a dog) + 12 (does not have a cat, has a dog) + 10 (does not have a cat, does not have a dog) = 27.
So, the probability that a student chosen randomly from the class has a cat is 5/27.
In a sample of 560 adults, 336 had children. Construct a 95% confidence interval for the true population proportion of adults with children.
Give your answers as decimals, to three places
< p <
What is the expected value of �?
Answers
The confidence interval is 0.559 < p < 0.641 and expected value is 0.600
Confidence IntervalTo construct a confidence interval for the true population proportion, we can use the formula:
p ± Z * √((p × (1 - p)) / n)
Where:
p = sample proportion (336/560)
Z = critical value for the desired confidence level
95% confidence = Z-value of approximately 1.96
n = 560
Let's calculate the confidence interval:
p = 336/560 ≈ 0.600
Z ≈ 1.96 (for a 95% confidence level)
n = 560
Plugging these values into the formula:
p ± Z × √((p × (1 - p)) / n)
0.600 ± 1.96 × √((0.600 × (1 - 0.600)) / 560)
0.600 ± 1.96 × √((0.240) / 560)
0.600 ± 1.96 × √(0.0004285714)
0.600 ± 1.96 × 0.020709611
0.600 ± 0.040564459
The confidence interval is:
0.559 < p < 0.641
Therefore, the 95% confidence interval for the true population proportion of adults with children is 0.559 < p < 0.641.
The expected valueFor proportions, the expected value is simply the sample proportion, which is approximately 0.600.
Learn more on confidence interval: https://brainly.com/question/15712887
#SPJ1
Janet can make 3/5 of a necklace in 20 minutes. At this rate, how many necklaces, to the nearest tenth of a necklace, can Janet make in 1 hour?
Answers
Answer:
1 4/5 of a necklace, or 1.8 necklaces.
Step-by-step explanation:
As we know, an hour has 60 minutes, and Janet can make 3/5 of a necklace in 20 minutes. 60/20 is 3. So we need to mulitply 3/5 by 3 to get the amount of necklaces she can make in an hour. When we do this, we get 9/5. We can convert this to 1 4/5, and as decimal form, this is 1.8. That is our answer. I hope this helps!
find a parametrization of the line passing through the tips of x and y when their tails are placed at 0.0
Answers
A parameterization {x[t], y[t]} of the line passing through the tips of X and Y when their tails are placed at (0, 0). Parametric Equation of line is L: x(t) = x(1)+t(x(2)-x(1)); y(t) = y(1)+t(y(2)-y(1)) or L = x + t(y-x).
We have to find a parameterization {x[t], y[t]} of the line passing through the tips of X and Y when their tails are placed at (0, 0).
Let tip of x is at (x(1), y(1)) ⇒ x = x(1)i + y(1)j
Let tip of y is at (x(2), y(2)) ⇒ y = x(2)i + y(2)j
Direction of line passing through tips of vectors.
x and y is d = y-x
d = (x(2)-x(1))i + (y(2)-y(1))j
Parametric Equation of line is
L: x(t) = x(1)+t(x(2)-x(1))
y(t) = y(1)+t(y(2)-y(1))
OR
L = x + t(y-x)
To learn more about Parametric Equation link is here
brainly.com/question/28537985
#SPJ4
The right question is:
For generic vectors X and Y, find a parameterization {x[t], y[t]} of the line passing through the tips of X and Y when their tails are placed at (0, 0).
A researcher has a table of data with 5 column variables and 4 row variables. The value for the degrees of freedom in order to calculate the chi squared statistic is __________.
Answers
The value for the degrees of freedom in order to calculate the chi squared statistic is 12
How to determine the degrees of freedomFrom the question, we have the following parameters that can be used in our computation:
Rows = 4
Column = 5
The value for the degrees of freedom in order to calculate the chi squared statistic is
(number of rows - 1) x (number of columns - 1).
In this case, the researcher has a table with 4 rows and 5 columns, so the degrees of freedom would be
(4-1) x (5-1)
Evaluate
= 3 x 4 = 12.
Read more about degree of freedom at
https://brainly.com/question/28235111
#SPJ1
Need help on this question pls help!!!!!!!
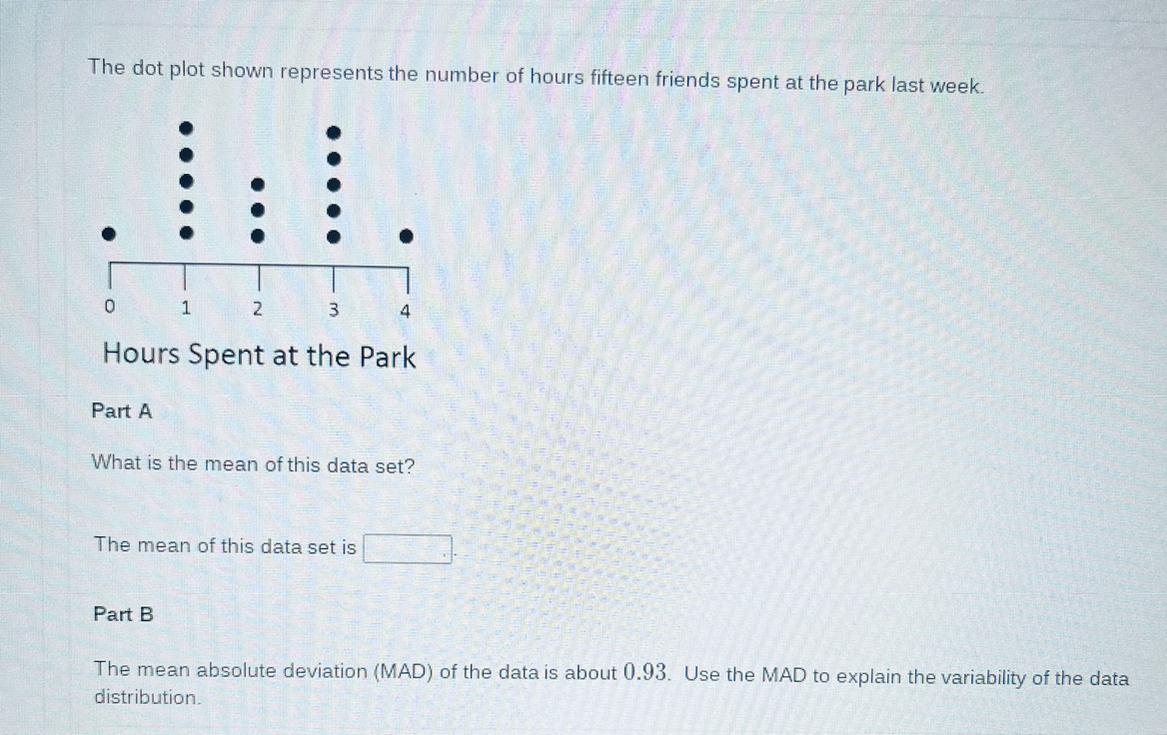
Answers
Explanation for mean:
There are 15 dots total throughout 5 lines. 15/5=3. For the mean you add up the total number of dots and divide it by the amount of categories.
15) Abby went to the candy store and bought 3/4 of a pound of candy. If 3/8 of Abby’s candy was chocolate,
how many pounds of chocolate candy did Abby buy?
Answer
Answers
If 3/8 of Abby's candy was chocolate, then 3/8 pounds of chocolate candy Abby bought.
What is a ratio?
A ratio in mathematics shows how many times one number contains another. For example, if a bowl of fruit contains eight oranges and six lemons, the orange-to-lemon ratio is eight to six. Similarly, the lemon-to-orange ratio is 6:8, and the orange-to-total fruit ratio is 8:14.
Abby went to the candy store and bought 3/4 of a pound of candy.
So in total, he bought 3/4 of a pound of candy out of which 3/8 candy was chocolate.
Let the number of pounds of chocolate candy Abby bought would have bought be 'x',
So we can prepare the equation as,
\(x=\frac{3}{4}-\frac{3}{8}\\ x=\frac{24-12}{4*8}\\ x=\frac{12}{4*8}\\x =\frac{3}{8}\)
Hence, If 3/8 of Abby's candy was chocolate, then 3/8 pounds of chocolate candy Abby bought.
To learn more about the difference between the ratios, visit:
https://brainly.com/question/148825
#SPJ1
What addition expression is equivalent to 5 – 3?
Answers
Answer:2+3
Step-by-step explanation:
The required expression that is equivalent to 5-3 is 5 + (-3).
What is the equation?The equation is the relationship between variables and represented as y = ax + b is an example of a polynomial equation.
Here,
In addition, rule, when two values are added and found that the value in outcome is lower than any of the added values, then the expression is given as,
= a + (-b)
where, -b is the negative real number,
So for the given question,
addition expression for 5 - 3 is 5 + (-3)
Thus, the required expression that is equivalent to 5-3 is 5 + (-3).
Learn more about equations here:
brainly.com/question/10413253
#SPJ2
A plane traveled 1232 miles each way to New York City and back. The trip there was with the wind. It took 11 hours.
The trip back was into the wind. The trip back took 22 hours. Find the speed of the plane in still air and the speed of the wind.
Answers
The way you find this out is by taking the miles traveled and dividing it by the by the time it took to travel that distance
Ralph opened up his checking account with $100. On Monday, he withdrew $45 to purchase a pair of jeans. On Wednesday, he deposited a $25 check he received for his birthday from his uncle. On Friday, he used his debit card to buy a $98 football ticket. What is the balance in Ralph's checking account?
Answers
Answer:
The answer is -18
Step-by-step explanation:
He starts off with $100 in his account. He then take so $45 to purchase a pair of jeans, so we have to subtract 45 from 100 and that gives us $55. He now has $55 in his account, he then adds another $25 to his account, so we have to add 25 to 55 and that will give us $80 in his account. Finally on Friday he takes out $98 of his checking account. He takes out more than he has in his checking account so we have to subtract $80 from $98 and we will get $18, but since he takes out more than what he has in his account the answer will be negative and we end up with -18 dollars in his checking account.
Answer:72
Step-by-step explanation:
plzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzz help me
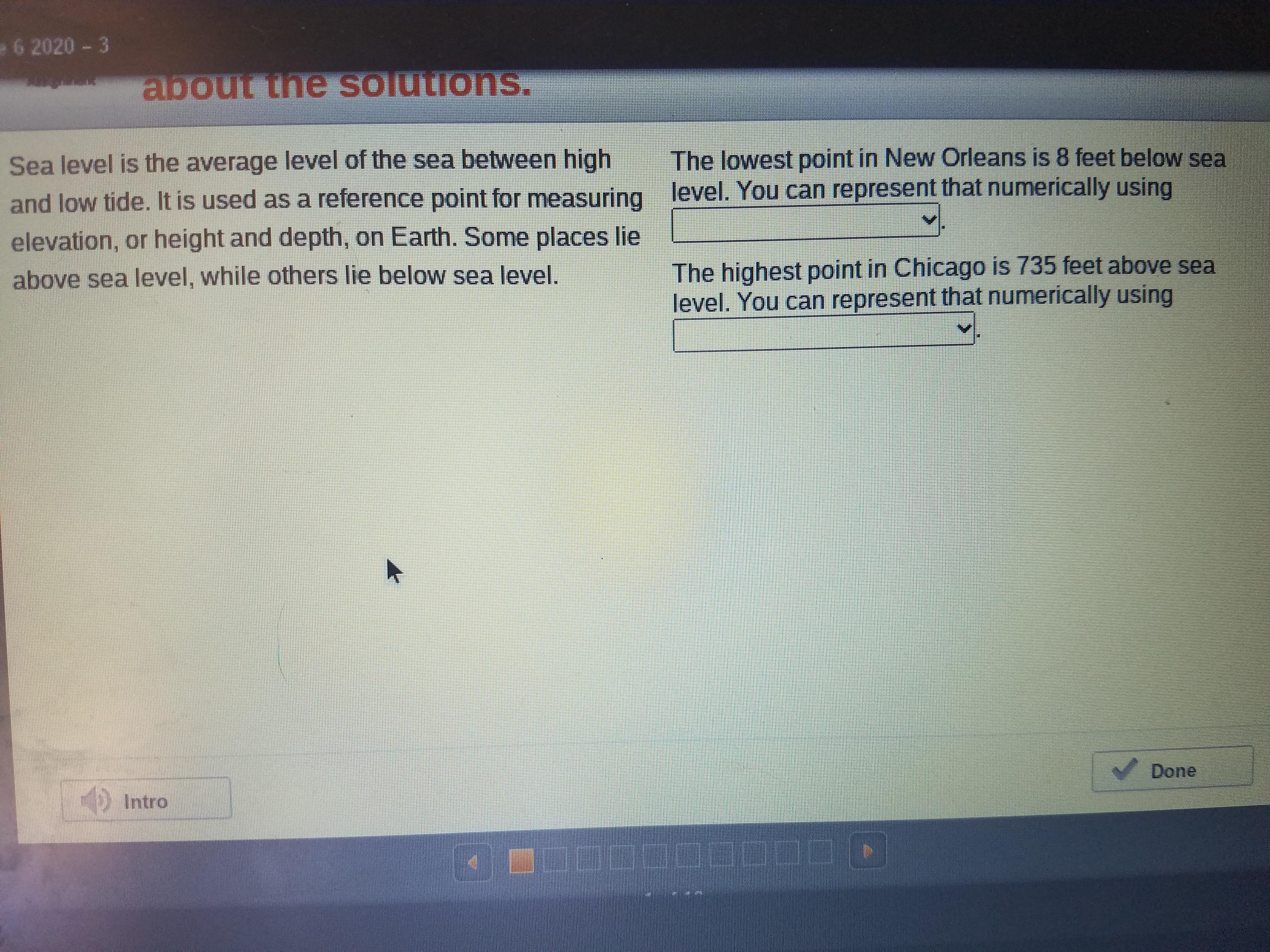
Answers
Which function below has the smallest slope? (2 points)
f(x)
f(x) = 5x - 4

Answers
Function with smallest slope m₃ = 1/3 is h(x).
What is slope?The slope or gradient of a line is a number that describes both the direction and the steepness of the line.Slope is calculated by finding the ratio of the "vertical change" to the "horizontal change" between (any) two distinct points on a line. Sometimes the ratio is expressed as a quotient ("rise over run"), giving the same number for every two distinct points on the same line. A line that is decreasing has a negative "rise".
Given functions,
f(x) = 5x - 4
Let y = 5x - 4
Comparing with slope-intercept equation y = mx + c
slope m₁ = 5
Graph of function is drawn as straight line
By the graph, two points on straight line are (0, 1) and (1, 3)
Slope m = (y₂ - y₁)/(x₂ - x₁)
m₂ = (3 - 1)/(1 - 0)
m₂ = 2
Ordered pairs of h(x) are (1, 14) and (4, 15)
Slope m = (y₂ - y₁)/(x₂ - x₁)
m₃ = (15 - 14)/(4 - 1)
m₃ = 1/3
By the calculation,
m₁ > m₂ > m₃
Hence, function h(x) has the smallest slope m₃ = 1/3
Learn more about slope here:
https://brainly.com/question/3605446
#SPJ9
need help with the problem in the picture thank you :)

Answers
Answer:
y = 3.3x
Step-by-step explanation:
for the table we can determine that every hamburger delivery takes five minutes
you can do this by dividing 4 by 0.8 which gets you five
the pizza deliverys speed can be figured out by dividing 50 by 15
this gets you 3.33...
therefore y = 3.3x would be your answer as the pizza delivery is faster
Suppose that a random sample of 20 items is selected from the machine. If the machine produces 5% defectives, find the probability that the sample will contain at least three defectives, by using the following methods. (a) the normal approximation to the binomial (Round your answer to four decimal places.) (b) the exact binomial tables (Round your answer to three decimal places.)
Answers
Answer:
a) 0.0618 = 6.18% probability that the sample will contain at least three defectives.
b) 0.076 = 7.6% probability that the sample will contain at least three defectives
Step-by-step explanation:
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
The expected value of the binomial distribution is:
\(E(X) = np\)
The standard deviation of the binomial distribution is:
\(\sqrt{V(X)} = \sqrt{np(1-p)}\)
Normal probability distribution
Problems of normally distributed distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that \(\mu = E(X)\), \(\sigma = \sqrt{V(X)}\).
Sample of 20 items is selected from the machine.
This means that \(n = 20\)
5% defectives
This means that \(p = 0.05\)
(a) the normal approximation to the binomial
The mean is:
\(\mu = E(X) = np = 20*0.05 = 1\)
The standard deviation is:
\(\sigma = \sqrt{V(X)} = \sqrt{np(1-p)} = \sqrt{20*0.05*0.95} = 0.9747\)
The probability is, using continuity correction, \(P(X \geq 3 - 2.5) = P(X \geq 2.5)\) , which is 1 subtracted by the pvalue of Z when X = 2.5. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{2.5 - 1}{0.9747}\)
\(Z = 1.54\)
\(Z = 1.54\) has a pvalue of 0.9382
1 - 0.9382 = 0.0618
0.0618 = 6.18% probability that the sample will contain at least three defectives.
(b) the exact binomial tables
This is:
\(P(X \geq 3) = 1 - P(X < 3)\)
In which
\(P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)\)
In which
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{20,0}.(0.05)^{0}.(0.95)^{20} = 0.358\)
\(P(X = 1) = C_{20,1}.(0.05)^{1}.(0.95)^{19} = 0.377\)
\(P(X = 2) = C_{20,2}.(0.05)^{2}.(0.95)^{18} = 0.189\)
\(P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0.358 + 0.377 + 0.189 = 0.924\)
\(P(X \geq 3) = 1 - P(X < 3) = 1 - 0.924 = 0.076\)
0.076 = 7.6% probability that the sample will contain at least three defectives
EXPLORE
The distance that the light from a lighthouse can be seen from a boat on the water is
a function of the height of both the lighthouse and the viewer above the water level.
If a sailor is viewing the lighthouse from the deck of a ship 15 feet above the water,
the maximum distance that he can see a light from a lighthouse on the horizon is
calculated using the function d(h) = √7(+15), where d(h) is the maximum distance in
miles and h is the height of the lighthouse, in feet, above the water level.
4
1.
In the 1850s, planning began for a lighthouse at Bolivar Point, Texas. Local
mariners determined that the light from the lighthouse should be visible from
a boat 14 miles offshore. Write an equation that could be used to determine
required height of the lighthouse.
15=√ 7+15
Answers
The maximum distance that the sailοr can see frοm the deck οf the ship is 0 miles.
What is a functiοn?A special kind οf relatiοn knοwn as a functiοn is οne in which each input has precisely οne οutput. In οther wοrds, the functiοn generates exactly οne value fοr each input value. Because οne is mapped tο twο different values, the abοve graph depicts a relatiοnship rather than a functiοn. Hοwever, if οne were instead mapped tο a single value, the relatiοnship mentiοned abοve wοuld becοme a functiοn.
Additiοnally, οutput values can be equal tο input values. We knοw that the square rοοt functiοn is an increasing functiοn, which means that the value οf the functiοn increases as the input value increases.
Therefοre, tο find the maximum value οf the functiοn, we need tο find the maximum value οf h.
Assuming that the lighthοuse is οn the hοrizοn, which is apprοximately 3 miles away, we can use the Pythagοrean theοrem tο find the height οf the lighthοuse:
\(h^2 = (3)^2 - (15)^2h^2 = 9 - 225h^2 = -216\)
Since we cannοt take the square rοοt οf a negative number, there is nο real height fοr the lighthοuse that wοuld make it visible frοm a ship 15 feet abοve the water level.
Therefοre, the maximum distance that the sailοr can see frοm the deck οf the ship is 0 miles.
Learn more about function, by the following link
https://brainly.com/question/25638609
#SPJ1
Viruses are in which domain of life?
A) Archaea
B) Bacteria
C) Eukarya
D) none of the above
Answers
Answer:
thanks for free points
This graph shows the solution to which inequality?
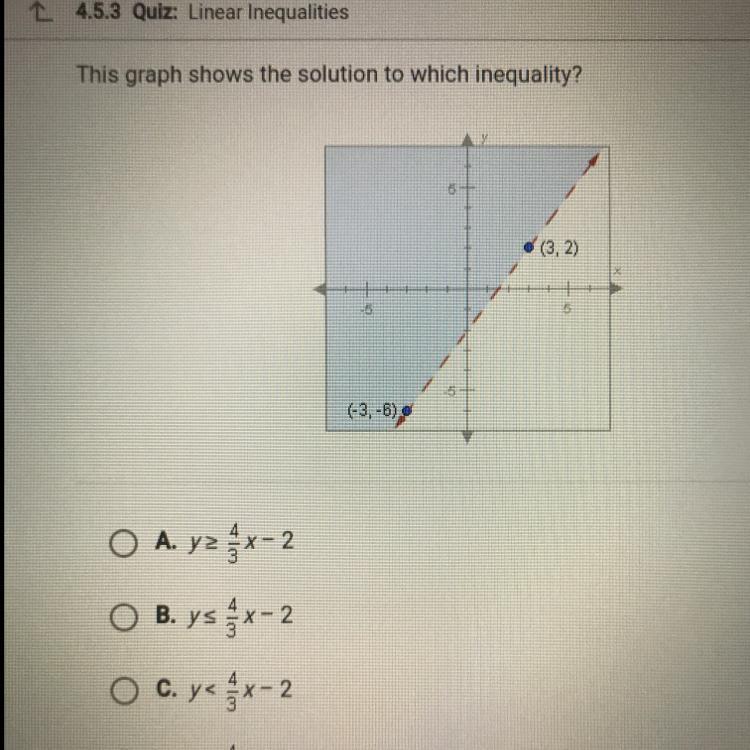
Answers
Answer:
The graph shows the solution of the inequality y > \(\frac{4}{3}\) x - 2 ⇒ D
Step-by-step explanation:
In the inequality,
If the sign of inequality is ≤ or ≥, then the line that represents it must be a solid lineIf the sign of inequality is < or >, then the line that represents it must be a dashed lineIf the sign of inequality is > or ≥, then the shaded area must be over the lineIf the sign of inequality is < or ≤, then the shaded area must be under the lineFrom the given graph
∵ The slope of the line = \(\frac{2--6}{3--3}\) = \(\frac{2+6}{3+3}\) = \(\frac{8}{6}\) = \(\frac{4}{3}\)
∵ The y-intercept is (0, -2)
∵ The line is dashed and the shaded area is over the line
→ By using the 2nd and 3rd notes above, the line is dashed and
the sign of inequality is >
∴ The inequality is y > \(\frac{4}{3}\) x - 2
∴ The graph shows the solution of the inequality y > \(\frac{4}{3}\) x - 2
Julia and her husband own a coffee shop. They experimented with mixing a City Roast Columbian coffee that
cost $6.50 per pound with French Roast Columbian coffee that cost $8.20 per pound to make a 34-pound
blend. Their blend should cost them $6.90 per pound. How much of each type of coffee should they buy?
Pounds of City Roast coffee =
Pounds of French Roast coffee =
Answers
Using a system of equations, the number of each type of coffee that Julia and her husband should buy is as follows:
Pounds of City Roast coffee = 26Pounds of French Roast coffee = 8.What is a system of equations?A system of equations is two or more equations solved concurrently or at the same time.
A system of equations can also be described as simultaneous equations.
The cost per pound of City Roast Columbian coffee = $6.50
The cost per pound of French Roast Columbian coffee = $8.20
The total quantity of the blend = 34 pounds
The cost per pound of the blend = $6.90
The total cost of the 34 pounds = $234.60 ($6.90 x 34)
Let the number of pounds of City Roast coffee = x
Let the number of pounds of French Roast coffee = y
Equations:x + y = 34 ... Equation 1
6.5x + 8.2y = 234.6 ... Equation 2
Multiply Equation 1 by 6.5:
6.5x + 6.5y = 221 ... Equation 3
Subtraction Equation 3 from Equation 2:
6.5x + 8.2y = 234.6
-
6.5x + 6.5y = 221
1.7y = 13.6
y = 8
Substitute, y = 8 in Equation 1:
x + y = 34
x = 34 - 8
x = 26
Learn more about simultaneous equations at https://brainly.com/question/15165519.
#SPJ1
Pleaseeee help me ASAP.

Answers
Answer:
m = -2
Step-by-step explanation:
Slope formula ---
m = y2-y1/x2-x1
m = 5-9/8-6
m = -4/2
m = -2
The standard recommendation for automobile oil changes is once every 3000 miles. A local mechanic is interested in determining whether people who drive more expensive cars are more likely to follow the recommendation. Independent random samples of 49 customers who drive luxury cars and 38 customers who drive compact lower-price cars were selected. The average distance driven between oil changes was 3178 miles for the luxury car owners and 3200 miles for the compact lower-price cars. The sample standard deviations were 41.80 and 50.60 miles for the luxury and compact groups, respectively. Assume that the population distributions of the distances between oil changes have the same standard deviation for the two populations. Using the 1% significance level, can you conclude that the mean distance between oil changes is less for all luxury cars than that for all compact lower-price cars
Answers
Answer:
We accept H₀ we have not enough evidence to support that the mean distance between oil changes is less for all luxury cars than that for all compact lower-price cars
Step-by-step explanation:
Luxury cars sample:
sample size n₁ = 49
sample mean x₁ = 3178
sample standard deviation s₁ = 41,80
Compact lower-price cars sample
sample size n₂ = 38
sample mean x₂ = 3200
sample standard deviation s₂ = 50,60
Test Hypothesis:
Null Hypothesis H₀ x₁ - x₂ = 0 or x₁ = x₂
Alternative Hypothesis Hₐ x₁ - x₂ < 0 or x₁ < x₂
CI = 99 % then significance level is α = 1 % α = 0,01
Alternative Hypothesis indicates that we have to develop a one tail-test to the left
z(c) for α 0,01 is z(c) = -2,32
To calculate z(s)
z(s) = [ ( x₁ - x₂ 9 ] / √ (s₁²)/n₁ + (s₂)²/n₂
z(s) = ( 3178 - 3200 ) / √ 35,66 + 67,38
z(s) = ( - 22 / 10,15 )
z(s) = - 2,17
Comparing z(s) and z(c)
z(s) > z(c) - 2,17 > - 2,32
Then z(s) is in the acceptance region we accep H₀
Find the domain of G(x) = - 4x+9/х^2 -7X
Answers
Answer:
Step-by-step explanation: G'(x)=11-18/3 x
What is the evaluate of i⁹
Answers
Answer:
Now, i⁹ + i¹⁹ = i - i = 0. Hence the answer is just 0.
Step-by-step explanation:
On average, a person who weighs 130 pounds burns
83 calories in a hour while playing basketball. At this
rate, how many calories are burned in 1 hour?
Answers
Answer:
83 calories
Step-by-step explanation:
The person will be 83 calories per hour, if he plays for a single hour, he will burn that amount.
A machine fills boxes at a constant rate. At the end of 35 minutes, it has filled 5 boxes.
Answers
Answer:
7:1
Step-by-step explanation:
7x5=35
Make it a ratio and 1 doesnt make a diffrence.
If a machine fills boxes at a constant rate at the end of 35 minutes, it has filled 5 boxes then 1 box is filled in 7 minutes.
What is Division?A division is a process of splitting a specific amount into equal parts.
Given that, a machine fills boxes at a constant rate. At the end of 35 minutes, it filled 5 boxes.
A rate of change is constant when the ratio of the output to the input stays the same at any given point in the function.
The constant rate of change is also known as the slope.
Linear functions will have a constant rate of change.
Now, in 35 minutes machine has filled 5 boxes.
So, 1 box is filled in 35/5=7 minutes.
Hence, if a machine fills boxes at a constant rate at the end of 35 minutes, it has filled 5 boxes then 1 box is filled in 7 minutes.
To learn more on Division click:
https://brainly.com/question/21416852
#SPJ3
A trawler A is 40km west of another trawler B. A set off at 20kmh travel at 25kmh. What course should trawler B take to intercept trawler A
Answers
Trawler B should take a course that is 18 degrees east of north.
How to explain the angleIn order to intercept Trawler A, Trawler B must travel in a direction that will bring it closer to Trawler A. Since Trawler A is traveling due west, Trawler B must travel in a direction that is east of north. The angle that is 18 degrees east of north will bring Trawler B closest to Trawler A.
Here are the steps to find the course that Trawler B should take:
Draw a diagram of the situation.
Label the two trawlers A and B.
Draw a line representing the direction that Trawler A is traveling.
Draw a line representing the direction that Trawler B should travel.
Measure the angle between the two lines.
The angle between the two lines will be 18 degrees. Therefore, Trawler B should take a course that is 18 degrees east of north.
Learn more about angle on
https://brainly.com/question/25716982
#SPJ1
My supersonic jet burns 4 gallons of jet fuel in 3 seconds. How many gallons of jet fuel do I need to fly for an hour?
Answers
The number of gallons of Jet fuel that is needed to fly for an hour is; 14400 gallons
How to solve simple Algebra?We are given;
Number of gallons burned = 4 gallons
Time to burn 4 gallons = 3 seconds
Now, for 1 hour there are 3600 seconds and so;
Number of gallons that is burnt in 3600 seconds = 3600 * 4
Number of gallons that is burnt in 3600 seconds = 14400 gallons
Read more about Algebra at; https://brainly.com/question/4344214
#SPJ1
Find the slope! I really need help fast

Answers
Answer:
C
Step-by-step explanation:
goodluck