Which factor provides the basis for the grading of newly diagnosed malignant tumors? size of the tumor x number of metastases degree of differentiation of the cells number of lymph nodes involved
Answers
The factor that provides the basis for the grading of newly diagnosed malignant tumours is degree of differentiation.
What is the degree of differentiation?The level of differentiation impacts an individual's capacity to control their emotions, thoughts, individuality, and connections to others. The degree of any differential equation can be obtained when it is expressed as a polynomial; otherwise, the degree cannot be defined.
The mechanisms by which immature cells develop into mature cells with particular roles are described in biology. This indicates the degree to which tumour tissue resembles the healthy tissue from which it originated in the context of cancer. Compared to poorly or undifferentiated cancer cells, well-differentiated cancer cells resemble normal cells more and grow and spread more slowly. Tumour grading systems, which vary for each form of cancer, use differentiation.
To know more about degree of differentiation, visit:
https://brainly.com/question/28104656
#SPJ4
Related Questions
Gabe is the human resources manager for the Advanced Scientific Research Lab. He has to record
the heights (in centimeters) and weights (in pounds) for each of the scientists in the lab.
Height distribution (cm): 178, 163, 174, 186, 154, 167, 167, 181, 159, 165, 177, 191, 158
Weight distribution (lbs): 157, 163, 190, 187, 183, 173, 184, 189, 193, 192, 177, 173, 168
What is the shape of the height and weight distribution?
Answers
Last option: The height and weight distributions, respectively, show positive and negative skews.
We know that,
Graphs are used to represent information in bar charts. To depict values, it makes use of bars that reach various heights. Vertical bars, horizontal bars, clustered bars (multiple bars that compare values within a category), and stacked bars are all possible options for bar charts.
we have,
There isn't a lot of data, but it shows that the weights have a negative skew and the heights have a positive skew, with the long tails pointing in opposite directions.
change/ starting point * 100
2.5 millions of books were sold in 1991.
Millions of books sold in 1992 equaled 3.4.
Change = 0.9 (in millions).
0.9/2.5 * 100
= 36%
The height and weight distributions, respectively, show positive and negative skews.
To know more about bar graphs visit:
brainly.com/question/13298277
#SPJ1
problem 3: for the function f (w3, w2, w1) = m1 + m3 + m4 + m6, show how the function f can be implemented using a 3-to-8 binary decoder and what is the truth table of your decoder?
Answers
To implement the function f(w1,w2,w3) = Σ m(0, 2, 4, 5, 7) using a 3 to 8 binary decoder and an OR gate, we can connect the input lines w1, w2, and w3 to the A, B, and C inputs of the decoder, respectively.
To implement the given function f(w1,w2,w3) = Σ m(0, 2, 4, 5, 7), we first need to convert it into a truth table as follows:
w1 w2 w3 f
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
Here, the binary values of w1, w2, and w3 are listed in the first three columns, and the corresponding value of f is listed in the fourth column. The expression Σ m(0, 2, 4, 5, 7) indicates that the function f should be equal to 1 for the minterms 0, 2, 4, 5, and 7.
We can use a 3 to 8 binary decoder to implement this function as follows:
The input lines of the decoder are w1, w2, and w3.
The outputs of the decoder are eight lines labeled Y0, Y1, Y2, Y3, Y4, Y5, Y6, and Y7, each corresponding to one of the possible input combinations of w1, w2, and w3.
The output line corresponding to each minterm that evaluates to 1 is connected to the input of an OR gate.
The output of the OR gate is the output of the function f.
Specifically, we can connect the input lines w1, w2, and w3 to the decoder as follows:
w1 is connected to the A input of the decoder.
w2 is connected to the B input of the decoder.
w3 is connected to the C input of the decoder.
The eight outputs of the decoder are connected to the inputs of an OR gate as follows:
Y0 is not connected to the OR gate since it corresponds to the input combination 000, which is not a minterm in the function.
Y1 is connected to one input of the OR gate since it corresponds to the input combination 001, which is a minterm in the function.
Y2 is not connected to the OR gate since it corresponds to the input combination 010, which is not a minterm in the function.
Y3 is connected to one input of the OR gate since it corresponds to the input combination 011, which is a minterm in the function.
Y4 is connected to one input of the OR gate since it corresponds to the input combination 100, which is a minterm in the function.
Y5 is connected to one input of the OR gate since it corresponds to the input combination 101, which is a minterm in the function.
Y6 is not connected to the OR gate since it corresponds to the input combination 110, which is not a minterm in the function.
Y7 is connected to one input of the OR gate since it corresponds to the input combination 111, which is a minterm in the function.
The other input of the OR gate is connected to ground (or logic 0).
Learn more about 3-to-8 binary decoder here
brainly.com/question/28945040
#SPJ4
An automatic filling machine is used to fill 2-litre bottles of cola. The machine’s output is known to be approximately Normal with a mean of 2.0 litres and a standard deviation of 0.01 litres. Output is monitored using means of samples of 5 observations.
Determine the upper and lower control limits that will include roughly 95.5 percent of the sample means.
If the means for 6 samples are 2.005, 2.001, 1.998, 2.002, 1.995 and 1.999, is the process in control?
Answers
The upper control limit (UCL) is approximately 2.0018 litres, and the lower control limit (LCL) is approximately 1.9982 litres, which would include roughly 95.5 percent of the sample means.
Now let's check if the process is in control using the given sample means:
To determine the upper and lower control limits for the sample means, we can use the formula:
Upper Control Limit (UCL) = Mean + (Z * Standard Deviation / sqrt(n))
Lower Control Limit (LCL) = Mean - (Z * Standard Deviation / sqrt(n))
In this case, we want to include roughly 95.5 percent of the sample means, which corresponds to a two-sided confidence level of 0.955. To find the appropriate Z-value for this confidence level, we can refer to the standard normal distribution table or use a calculator.
For a two-sided confidence level of 0.955, the Z-value is approximately 1.96.
Given:
Mean = 2.0 litres
Standard Deviation = 0.01 litres
Sample size (n) = 5
Using the formula, we can calculate the upper and lower control limits:
UCL = 2.0 + (1.96 * 0.01 / sqrt(5))
LCL = 2.0 - (1.96 * 0.01 / sqrt(5))
Calculating the values:
UCL ≈ 2.0018 litres
LCL ≈ 1.9982 litres
Therefore, the upper control limit (UCL) is approximately 2.0018 litres, and the lower control limit (LCL) is approximately 1.9982 litres, which would include roughly 95.5 percent of the sample means.
Now let's check if the process is in control using the given sample means:
Mean of the sample means = (2.005 + 2.001 + 1.998 + 2.002 + 1.995 + 1.999) / 6 ≈ 1.9997
Since the mean of the sample means falls within the control limits (between UCL and LCL), we can conclude that the process is in control.
Learn more about means from
https://brainly.com/question/1136789
#SPJ11
I WILL MARK BRAINLIEST IT WAS DUE LAST WEEK PLS HELP

Answers
Answer:
\(y=\frac{3}{2}x-6\)
Step-by-step explanation:
y=Mx+b is slope intercept form
M- slope
b- y intercept
We know b because when x is zero y is -6 so that is the y intercept
b=-6
Now to fin the slope we use y2-y1/x2-x1
0-(-3)/4-2
3/2
m=3/2
So we just put it all into the equation to get
y=3/2x-6
Hopes this helps
Answer: i'm writeing this so you can mark the other person brainliest
Step-by-step explanation:
A repair bill for your car is $553. The parts cost $265. The labor cost is $48 per hour. Write and solve an equation to find the number of hours of labor spent repairing the car. Record the solution (answer),
Answers
Answer:
6 hours
Step-by-step explanation:
Let the labor hours be x.
The bill comprises of parts cost plus labor cost. Labor cost is hours times the cost per hour. Then we have equation:
265 + 48x = 55348x = 553 - 26548x = 288x = 288/48x= 6So the answer is 6 hours.
Jennifer and Jane are best friends. They placed a map of their town on a coordinate grid and found the point at which each of their house lies. If Jennifer’s house lies at (9, 7) and Jane’s house is at (15, 9) and they wanted to meet in the middle, what are the coordinates of the place they should meet?
Answers
The coordinates of the place that Jennifer and Jane should meet is (\(\frac{24}{2} \frac{16}{2}\)). Check more about coordinates below?
What is the coordinates about?Based on the fact that:
Jennifer’s house lies at (9, 7),
Jane’s house lies at (15, 9) ,
Therefore, the equation will be:
(9, 7) = (x₁, y₁)
(15, 9) = (x₂, y₂)
P= (\(\frac{x₁ + x₂ }{2} \frac{y₁ + y₂}{2}\))
P= \(\frac{9+ 15 }{2} \frac{7 + 9}{2}\)
Therefore, P= 24/2, 16/2.
Learn more about coordinates from
https://brainly.com/question/17206319
#SPJ2
HELP
Answers available are on the picture

Answers
Answer:
\(360 = 2\pi \\\\90 = \frac{2\pi }{4} =\frac{\pi }{2} \\\\180 = \pi \\\\270 = \frac{6\pi }{4} = \frac{3\pi }{2}\)
the number of bacteria in experiment can be presented by f(x) = 4 where x represents the numbers of hours
What is x when fx=64
retake!!!

Answers
Answer: A
Step-by-step explanation:
4^3=64.
Option:-
A ) x = 3; in the 3rd hour there will be bacteria.\( \: \)
Given:-
\( \sf{f ( x ) = 4^x}\)\( \: \)
To prove:-
\( \sf \: f ( x ) = 64\)\( \: \)
Solution:-
\( \sf \: f ( x ) = 4^x.\)\( \: \)
put the value of x = 3
\( \sf \: f ( 3 ) = 4^3\)\( \: \)
\( \sf \: f ( 3 ) = 64 \)\( \: \)
━━━━━━━━━━━━━━━━━━━━━━━━━
hope it helps! :)
i need help can someone help please?

Answers
Answer:
None
Step-by-step explanation:
It would be easier to ask your teacher instead of getting wrong answers from random people. Ever think of that :0
Need help on this question please!!!

Answers
To tell if a graph is a function. Draw lines down the y axis. If the lines touches the line on the graph twice or more, it’s not a function (also known as the vertical line test, if u wanna search it).
A party tent is used for an outdoor event. Ropes of equal length support each tent pole. The angle each rope makes with the ground is 52°.
What is the height of each tent pole?
Enter your answer in the box. Round only your final answer to the nearest tenth.
ftA party tent is used for an outdoor event. Ropes of equal length support each tent pole. The angle each rope makes with the ground is 52°.
What is the height of each tent pole?
Enter your answer in the box. Round only your final answer to the nearest tenth.
ft
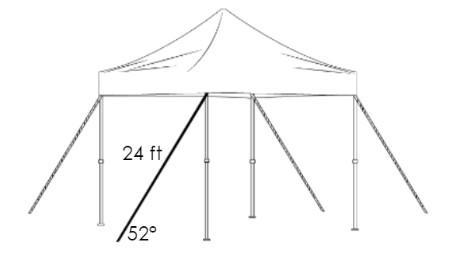
Answers
if the ropes are 10 feet long, for example, the height of each tent pole would be approximately 8 feet.
how to calculate the height of each tent poleLet's call the height of each tent pole "h" and the length of each rope "r". We can use trigonometry to relate these variables.
We know that the angle each rope makes with the ground is 52°. This means that the angle between the rope and the side of the tent (which is perpendicular to the ground) is 90° - 52° = 38°.
We can use the trigonometric function tangent (tan) to relate this angle to the height and length of the rope:
tan(38°) = h/r
To solve for "h", we can rearrange this equation:
h = r * tan(38°)
We know that the ropes are of equal length, so we only need to find the value of "h" once. To find the length of the ropes, we would need additional information.
Using a calculator, we can evaluate tan(38°) to be approximately 0.7813. Therefore, the height of each tent pole is:
h = r * 0.7813
We can't determine a specific numerical value for "h" without knowing the length of the ropes, but we can express the answer in terms of "r" and round to the nearest tenth of a foot:
h ≈ 0.8r ft
So, if the ropes are 10 feet long, for example, the height of each tent pole would be approximately 8 feet.
Learn more about trigonometric function at https://brainly.com/question/25618616
#SPJ1
at a certain grocery checkout counter, the average waiting time is 2.5 minutes. suppose the waiting times follow an exponential density function. (a) write the equation for the exponential distribution of waiting times. e(t) = graph the equation and locate the mean waiting time on the graph. webassign plot webassign plot webassign plot webassign plot (b) what is the likelihood that a customer waits less than 1 minutes to check out? (round your answer to one decimal place.) % (c) what is the probability of waiting between 4 and 6 minutes? (round your answer to one decimal place.) % (d) what is the probability of waiting more than 5 minutes to check out? (round your answer to one decimal place.) % need help? read it
Answers
a) The equation for the exponential distribution of waiting times is given by \(f(x) = \lambda e^{-\lambda x}\)
b) The probability of waiting less than 2 minutes to check out is 0.427
c) The probability of waiting between 4 and 6 minutes is 0.242
d) The probability of waiting more than 5 minutes to check out is 0.082
a. The equation for the exponential distribution of waiting times is given by:
\(f(x) = \lambda e^{-\lambda x}\)
where λ is the rate parameter of the distribution, and e is the natural logarithmic constant (approximately equal to 2.71828). The graph of the exponential distribution is a decreasing curve that starts at λ and approaches zero as x approaches infinity. The mean waiting time, denoted by E(X), is equal to 1/λ.
b. To find the probability that a customer waits less than 2 minutes to check out, we need to calculate the area under the exponential distribution curve between zero and 2 minutes. This can be expressed mathematically as:
P(X < 2) = \(\int_0^2 \lambda e^{-\lambda x} dx\)
Solving this integral yields:
P(X < 2) = 1 - \(e^{(-2\lambda)}\)
Substituting the given average waiting time of 2.5 minutes into the formula for the mean waiting time, we can calculate λ as:
E(X) = 1/λ
2.5 = 1/λ
λ = 0.4
Therefore, the probability of waiting less than 2 minutes to check out is:
P(X < 2) = 1 - \(e^{-2*0.4}\)
P(X < 2) ≈ 0.427
c. To find the probability of waiting between 2 and 4 minutes, we need to calculate the area under the exponential distribution curve between 2 and 4 minutes. This can be expressed mathematically as:
P(2 < X < 4) =\(\int_2^4 \lambda e^{(-\lambda x)} dx\)
Solving this integral yields:
P(2 < X < 4) = \(e^{(-2\lambda)} - e^{(-4\lambda)}\)
Substituting the value of λ obtained in part (b), we get:
P(2 < X < 4) = \(e^{(-20.4)} - e^{(-40.4)}\)
P(2 < X < 4) ≈ 0.242
d. To find the probability of waiting more than 5 minutes to check out, we need to calculate the area under the exponential distribution curve to the right of 5 minutes. This can be expressed mathematically as:
P(X > 5) = \(\int_5^{ \infty} \lambda e^{(-\lambda x)} dx\)
Solving this integral yields:
P(X > 5) = \(e^{(-5\lambda)}\)
Substituting the value of λ obtained in part (b), we get:
P(X > 5) = \(e^{(-5*0.4)}\)
P(X > 5) ≈ 0.082
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
At any time t > 0,the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized ad tlie number of words tlat have not been memorized. If 2 denotes the number of words memorized at time t, which differential equation models this situation? Assume kis a positive constant; A. d k dt B. d k ( - M) dt C d k(M - 2) dt D. d =Rt(M -t) dt
Answers
The differential equation that models this situation is dx/dt = kx(M - x) (option c).
To determine the differential equation that models the situation, let's analyze the problem statement.
The rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized.
Let's denote the number of words memorized as "a" and the number of words not yet memorized as "M - a" (where M is the total number of words in the list).
The problem states that the rate of memorization is proportional to the product of "a" and "M - a". We can express this mathematically as:
Rate of memorization ∝ a * (M - a)
To convert this proportionality into an equation, we introduce a positive constant k:
Rate of memorization = k * a * (M - a)
The left side of the equation represents the rate of change of the number of words memorized (da/dt), and the right side represents the product of "a" and "M - a" multiplied by the constant k.
Therefore, the differential equation that models this situation is:
da/dt = k * a * (M - a)
Comparing this with the given options, we can see that the correct choice is option C:
dx/dt = k * x * (M - x)
The complete question is:
At any time t > 0 the rate at which a person can memorize a list of M words is proportional to the product of the number of words memorized and the number of words that have not been memorized. If a denotes the number of words memorized at time t, which differential equation models this situation? Assume k is a positive constant.
A. dx/dt = kx
B. dx/dt = kx(x - M)
C. dx/dt = kx(M - x)
D. dx/dt = kt(M - t)
To know more about differential equation:
https://brainly.com/question/32524608
#SPJ4
ASAP and God bless you

Answers
Answer: $384
Step-by-step explanation:
In part A, you calculated ratios with the help of GeoGebra. Now you'll use the distance formula to calculate more ratios. Choose two line segments
in the logo that are not horizontal or vertical. For n = 3, calculate the lengths of the line segments in the image and in the preimage using the
distance formula d = (x2 – x)? + (y2 – yı)?. When you're through, find the ratio of the segment length in the image to the corresponding
segment length in the preimage. How do your ratios compare to the scale factor n = 3? Show your work.
Answers
Answer:
Step-by-step explanation:

Answer:
LOOK AT THE OTHER ONE AND COPY N PASTE THA PICTURE
Step-by-step explanation:
Choose the correct answer below. A. The statement is true. If a set contains fewer vectors than there are entries in the vectors, then there are less variables than equations, so there cannot be any free variables in the equation Ax=0. B. The statement is false. A set of vectors is linearly independent if none of the vectors can be written as a linear combination of the others. If there are fewer vectors than entries in the vectors, then at least one of the vectors must be written as a linear combination of the others. C. The statement is false. There exists a set that contains fewer vectors than there are entries in the vectors that is linearly dependent. One example is a set consisting of two vectors where one of the vectors is a scalar multiple of the other vector. D. The statement is true. There exists a set that contains fewer vectors than there are entries in the vectors that is linearly independent. One example is a set consisting of two vectors where one of the vectors is not a scalar multiple of the other vector.
Answers
The correct option among the options that are given in the question is the third option or option "C". The statement is false. There exists a set that contains fewer vectors than there are entries in the vectors that is linearly dependent. One example is a set consisting of two vectors where one of the vectors is a scalar multiple of the other vector.
Linearly dependent and independent sets of vectors are used in the study of linear algebra and have been discussed in depth to understand the properties of these sets of vectors.
Linearly independent vectors: Vectors that are independent of each other and are not multiples of each other are called linearly independent vectors. No vector in a set can be defined as a linear combination of the others.
Linearly dependent vectors: In contrast, vectors that are not independent and can be described as linear combinations of each other are referred to as linearly dependent vectors.
Therefore, we can conclude that The statement is false. There exists a set that contains fewer vectors than there are entries in the vectors that is linearly dependent. One example is a set consisting of two vectors where one of the vectors is a scalar multiple of the other vector.
So, the correct answer is option C, The statement is false. There exists a set that contains fewer vectors than there are entries in the vectors that is linearly dependent. One example is a set consisting of two vectors where one of the vectors is a scalar multiple of the other vector.
To learn more aboout Linearly dependent: https://brainly.com/question/30556318
#SPJ11
Write 25/60 and 8/20 as fractions in simplest form. Then determine whether the ratios form a proportion
Answers
Answer:
8/20= 4/5
25/60= 5/12
Step-by-step explanation:
8÷4
Answer:
25/60 = 5/12
8/20 = 2/5
The Ratios do not form a proportion
Step-by-step explanation:
25/60:
25 ÷ 5/60 ÷ 5
= 5/12
8/20:
8 ÷ 4/20 ÷ 4
= 2/5
5/12 ≠ 2/5
The ratios are not proportional.
use the following functions to solve g(12)
f(x) = -2x + 1
g(x) = 1/2x - 1
A: 6
B: 7
C: 5
D: 4
Answers
Answer:
g(12) = 5
C
Step-by-step explanation:
Since the question asks what would be the answer to the equation if x=12, you just subsitute x for 12 which would be 1/2(12) - 1 which equals 6-1 which would equal 5.
Assume the length X, in minutes, of particular type of telephone conversation is random variable with probability density function 7/ 5>0, cawhere. f(f) (o Determine the mean length E(X) of this type of telephone conversation Find the variance and standard deviation of X. Find EI(X + 5)^2].
Answers
The mean length of this type of telephone conversation is E(X) = 7/5.
This means that on average, these conversations last 7/5 units of time. Additionally, the variance of X is Var(X) = 49/25, which indicates the amount of variation in the lengths of these conversations. The standard deviation, σ, is equal to 7/5, which is a measure of how spread out the data is.
Furthermore, if we add 5 to each conversation length, square the result, and take the expected value, we get E((X+5)2) = 949/25.
This calculation gives us an idea of the expected value of the squared deviations of the conversation lengths from their mean value, after adding 5 to each length.
This value can be used to assess the variability of the data and its potential impact on the outcomes of interest. Overall, these statistical measures provide useful information about the distribution of conversation lengths, and can inform decision-making in various contexts.
To learn more about mean, refer below:
https://brainly.com/question/31101410
#SPJ11
37. Perform the following binary multiplications, assuming unsigned integers: b) 10011 x 1011
Answers
The binary multiplication of 10011 and 1011, assuming unsigned integers, is 1000101 (209 in decimal).
To perform the binary multiplication of 10011 (19 in decimal) and 1011 (11 in decimal), follow these steps:
1. Write down the two binary numbers, with the larger one on top:
10011
x 1011
2. Starting from the rightmost digit of the bottom number, multiply it by the entire top number, writing the product below, aligned with the current digit:
10011
x 1011
-----
10011 (1 * 10011)
3. Move one position to the left in the bottom number, and repeat step 2. Add a zero to the rightmost position of the product to account for the place value:
10011
x 1011
-----
10011
00000 (0 * 10011)
4. Continue this process for each digit in the bottom number:
10011
x 1011
-----
10011
00000
10011 (1 * 10011)
5. Finally, add all the products together:
10011
x 1011
-----
10011
00000
10011
-----
1000101 (final product)
So, the binary multiplication of 10011 and 1011, assuming unsigned integers, is 1000101 (209 in decimal).
Learn more about integers here:
https://brainly.com/question/30461111
#SPJ11
what is 2 1/4 - 5 2/3
Answers
Answer:
-41/12 or -3 5/12
Step-by-step explanation:
4*2 +1 = 9, 5 * 3 + 2 = 17
9/4 - 17/3
27/12 - 68/12
= -41/12 or -3 5/12
(-2, 8) (9, 10) (1,7) (3, 9) (10, 12)
Function
Not a Function
Answers
Answer: function
Step-by-step explanation: To determine whether the relation shown here
is a function, remember that a relation is a function if each x term
corresponds to exactly one y term.
In the data set show, each x term, -2, 9, 1, 3, and 10 appears only once.
This means that each x term corresponds to exactly one y term.
So yes, the relation is a function.
Evaluate 5−1/−90. Write your answer as a fraction in simplest form.
Answers
Answer:
2/-45
Step-by-step explanation:
5-1 = 4
4/-90 = 2/-45
Hope that helps
commutative property under integers and rational numbers with examples
Answers
Step-by-step explanation:
Commutative law under addition says- p + q = q + p. Commutative law under multiplication says p x q = q x p. Note- Rational numbers, integers and whole numbers are commutative under addition and multiplication. Rational numbers, integers and whole numbers are non commutative under subtraction and division.
PLEASE HELP ME IT'S DUE TODAY AND IT COULD HELP MY GRADE A LOT

Answers
Answer:
c = 13
m∡A = 60°
m∡B = 30°
Step-by-step explanation:
This is a 5-12-13 triangle. However, to make sure, I will put the steps.
Allow for each sides to be denoted as a-b-c, in which c is the hypotenuse (longest side). Set the equation:
a² + b² = c²
Plug in the corresponding numbers to the corresponding variables:
5² + 12² = c²
Simplify. First, solve the exponents, and then add:
(5²) = 5 * 5 = 25
(12²) = 12 * 12 = 144
25 + 144 = c²
c² = 169
Note the equal sign, what you do to one side, you do to the other. Isolate the variable, c, by rooting both sides:
√c² = √169
c = √169 = √(13 * 13) = 13
c = 13
13 is your answer for c.
Note the measurements of the angles. We know that this is a 30-60-90 triangle, and so it will be easy to figure it out. Note that the corresponding angles will depend on that of the opposite side's measurement lengths. The hypotenuse will always be on the opposite side of the largest angle (as given), as c, the longest side, is opposite of ∡C, which is the largest angle (90°). Based on this information, it means that ∡A would be 60° (as it is opposite of the middle number, 12), and ∡B would be 30° (opposite of the smallest number, 5).
PLZZ HELP WILL MARK BRAINLIEST
Ian has a bank account that earns interest. The value, V, in dollars, of Ian's account after t years can be modeled by the exponential function V(t)=5000(1.025)t.
Ian claims that the value of his bank account grows by an equal factor each year. To prove his claim, which equation must he show to be true?
V(t+1)/V(t)=1.025
V(t+1)−V(t)=1.025
V(t)−V(t+1)=1.025
V(t)/V(t+1)=1.025
Answers
Answer:
the third one I think please see be right
Given the triangle, find the length of X. Give your answer in simpliest radical form.

Answers
Answer:
x = 4\(\sqrt{2}\)
Step-by-step explanation:
using the cosine ratio in the lower right triangle and the exact value
cos45° = \(\frac{1}{\sqrt{2} } }\) , then
cos45° = \(\frac{adjacent}{hypotenuse}\) = \(\frac{4}{x}\) = \(\frac{1}{\sqrt{2} }\) ( cross- multiply )
x = 4\(\sqrt{2}\)
Aldo went to the store and purchased 8 notebooks for
school. He gave the cashier a $20.00 bill and received
$4.08. Each notebook cost the same amount. Describe the
process you would use to find the cost of each notebook.
Answers
Step-by-step explanation:
Start with $20.00.
Subtract the change, $4.08, from $20.00 to find out the amount he spent on 8 notebooks.
Then divide the amount he spent by 8 to find the cost of one notebook.
Answer:
$1.99
Step-by-step explanation:
20 - 4.08 = $15.92
15.92 divided by 8 = $1.99
Can you help me do 1+1
Answers
Answer:
The answer to 1+1 is 2.
Answer:
2
Step-by-step explanation:
pls pls pls pls pls pls pls answer it pls :(

Answers
Answer:
1. BC≅DC ; AC≅EC
2. ∠BCD≅∠ACE and ∠BCA≅∠DCE
3. SAS (side angle side)
Step-by-step explanation: