Answers
Answer:
The answer is C. (4x+12)+8x=180
Answer:
C
Step-by-step explanation:
alt. interior angles are congruent, so don't worry about y
also, because of alt. int. angles, we know that (4x+12)+8x=180
we can solve it by grouping like terms to get x=14
Related Questions
Can you people please help me with some more math that I can't understand?
Please see the following image below:

Answers
Answer:
He would collect 28 cans
Step-by-step explanation:
Ethan = 1/3
84 * 1/3 = 28
Answer:
28 cans were collected by Ethan
Step-by-step explanation:
It says that the total amount of cans collected was 84 cans. Of the 84 total cans, Ethan collected 1/3 of them. To find the number of cans Ethan collected, you would multiply 84 • 1/3. (You could also divide 84 by 3 in this case)
84 • 1/3 = 28
What is 2a+50=5a-4? Thank you for your time.
Answers
Answer:
2a+50=5a-4
5a-2a=50+4
3a=54
a=18
Answer:
\(a=18\)
Step-by-step explanation:
\(2a+50=5a-4\\\mathrm{Subtract\:}50\mathrm{\:from\:both\:sides}\\2a+50-50=5a-4-50\\Simplify\\2a=5a-54\\\mathrm{Subtract\:}5a\mathrm{\:from\:both\:sides}\\2a-5a=5a-54-5a\\\mathrm{Simplify}\\-3a=-54\\\mathrm{Divide\:both\:sides\:by\:}-3\\\frac{-3a}{-3}=\frac{-54}{-3}\\Simplify\\\frac{-3a}{-3}=\frac{-54}{-3}\\\mathrm{Simplify\:}\frac{-3a}{-3}:\quad a\\\frac{-3a}{-3}\\\mathrm{Apply\:the\:fraction\:rule}:\quad \frac{-a}{-b}=\frac{a}{b}\\=\frac{3a}{3}\\\mathrm{Divide\:the\:numbers:}\:\frac{3}{3}=1\)
\(=a\\\mathrm{Simplify\:}\frac{-54}{-3}:\quad 18\\\frac{-54}{-3}\\\mathrm{Apply\:the\:fraction\:rule}:\quad \frac{-a}{-b}=\frac{a}{b}\\=\frac{54}{3}\\\mathrm{Divide\:the\:numbers:}\:\frac{54}{3}=18\\=18\\a=18\)
Help me please !!!
Which explicit formula describes the arithmetic
sequence {19, 14, 9, 4, ...}

Answers
Answer:
\(a_n=19+(n-1)(-5)\)
Step-by-step explanation:
The explicit formula for an arithmetic sequence is \(a_n=a_1+(n-1)d\) where \(a_n\) is the \(n\)th term and \(d\) is the common difference.
In this problem, we can see that the first term of the sequence is \(a_1=19\) and the common difference is \(d=-5\) since 5 is being subtracted each consecutive term.
Therefore, the explicit formula that describes the given arithmetic sequence is \(a_n=19+(n-1)(-5)\)
Answer:
option 2
Step-by-step explanation:
Let { a1, a2, a3, a4, ... } be the sequence.
now the 1st term (a1) will have a value when n = 1.
similarly, all the other terms will have the values given when we substitute their respective n values into the explicit formula or fibonacci sequence.
thus, check if the 1st term is 19 by using option 2
an = 19 + (n-1)(-5)
an = 19 + (n-1)(-5) ....n = 1
an = 19 + (n-1)(-5) ....n = 1 a1 = 19 + (1-1)(-5) = 19 + 0 = 19. so it's accurate so far.
next, check a2 where n = 2.
a2 = 19 + (2-1)(-5) = 19 - 5 = 14. ....
n = 3
a3 = 19 + (3-1)(-5) = 19 - 10 = 9.
hence the conclusion from this pattern.
Which expression is equal to (x+7)(−5x²+12x−2)?
Answers
Answer:
-5x^3-23x^2+82x-14
Step-by-step explanation:
can someone help? i think its false but is cos to the negative one the same as sec?

Answers
Answer:
True
Step-by-step explanation:
Cos^-1 = 1/ cos = sec x
Answer: True
Step-by-step explanation:
When the cos(ine) function is raised to the negative first power, we find the reciprocal. This will be the case for most functions and numbers.
2/5+3/8= i will give brainliest
Answers
Q3. Integrate by using partial fraction, ∫ (x+1)(x−2)(x+3)
2x 2
+9x−35
dx. Q4. Find the area of the region bounded by the curves y=x 2
+4 lines y=x,x=0 and x=3.
Answers
The area of the region bounded by the curves y=x^2 +4, y=x, x=0 and x=3 is 16.5 square units.
How to find the area of the region ?Integrate the function using partial fractions:
∫ [(x+1)(x−2)(x+3)] / [2x² + 9x - 35] dx
The area A between the curves y=f(x) and y=g(x) from x=a to x=b is given by:
A = ∫ |f(x) - g(x)| dx, from x=a to x=b
The absolute difference between these two functions on this interval is:
|x² + 4 - x|
x² + 4 - x = x² - x + 4
Therefore, the area A is:
A = ∫ (x² - x + 4) dx, from x=0 to x=3
A = [1/3x³ - 1/2x² + 4x] (from 0 to 3)
= (1/33³ - 1/23² + 43) - (1/30³ - 1/20² + 40)
= 9 - 4.5 + 12
= 16.5 square units
Find out more on area at https://brainly.com/question/20464528
#SPJ4
3. Integrate - \int \frac{(x+1)(x-2)(x+3)}{2x^{2}+9x-35} dx = \frac{54}{7} \ln|x-5| + \frac{5}{12} \ln|2x+7| + C
4. The required area of the region is 27/2.
3. Integrating using partial fractions:
To solve the following integral, we will begin by performing the partial fraction decomposition of the given function. Here, we have a quadratic factor, so we will begin by setting the function equal to the sum of two fractions that have first-degree polynomial denominators like this :
\frac{(x+1)(x-2)(x+3)}{2x^{2}+9x-35} = \frac{A}{x-5}+\frac{B}{2x+7}
Since the denominators are of different degrees, we must find the least common denominator of both sides.
That is (x-5)(2x+7)
Multiplying by this common denominator, we have (x+1)(x-2)(x+3) = A(2x+7) + B(x-5)
Let us now solve for A and B by substituting the values of x:
\begin{aligned}\text{Let }x&=5:\ \ 6 \cdot 8 \cdot 8 = 7A\\A&=\frac{384}{7}\\\\\text{Let }x&=-\frac{7}{2}:\ \ \frac{5}{2} \cdot -\frac{9}{2} \cdot -\frac{1}{2} = -\frac{9}{2}B\\B&=\frac{5}{6}\end{aligned}
Therefore,\begin{aligned}\frac{(x+1)(x-2)(x+3)}{2x^{2}+9x-35} &= \frac{\frac{384}{7}}{x-5}+\frac{\frac{5}{6}}{2x+7}\\\\&=\frac{54}{7} \int \frac{1}{x-5}dx + \frac{5}{6} \int \frac{1}{2x+7}dx\\\\&=\frac{54}{7} \ln|x-5| + \frac{5}{12} \ln|2x+7| + C\end{aligned}
Thus,\int \frac{(x+1)(x-2)(x+3)}{2x^{2}+9x-35} dx = \frac{54}{7} \ln|x-5| + \frac{5}{12} \ln|2x+7| + C
4. Area of the region bounded by the curves:
The area of the region bounded by the curves y=x^2, y=x, x=0, and x=3 is given by\int_0^3 (x^2-x) dx = \frac{1}{3}x^3-\frac{1}{2}x^2 \Bigg|_0^3 = \boxed{\frac{27}{2}}
Hence, the required area of the region is 27/2.
learn more about Integrate on:
https://brainly.com/question/30094386
#SPJ11
Find the surface area of the portion S of the cone z^2 = x^2 + y^2 where z>/ 0 contained within the cylinder y^2 + z^2 < 1
Answers
The surface area of the portion S of the cone z^2 = x^2 + y^2 where z>/ 0 contained within the cylinder y^2 + z^2 < 1 is 8π.
The cone is defined by the equation z^2 = x^2 + y^2.
The cylinder is defined by the equation y^2 + z^2 < 1.
The intersection of the cone and the cylinder is a surface that is part of a cone and part of a cylinder.
The surface area of the cone is given by the formula A = πr^2h, where r is the radius of the base and h is the height of the cone.
The radius of the base of the cone is equal to 1, and the height of the cone is equal to √2. Therefore, the surface area of the cone is π(1)^2(√2) = √2π.
The surface area of the cylinder is given by the formula A = 2πrh, where r is the radius of the base and h is the height of the cylinder.
The radius of the base of the cylinder is equal to 1, and the height of the cylinder is equal to 1. Therefore, the surface area of the cylinder is 2π(1)(1) = 2π.
The surface area of the intersection of the cone and the cylinder is equal to the surface area of the cone minus the surface area of the cylinder. Therefore, the surface area of the intersection is √2π - 2π = 8π.
To learn more about cones click here: brainly.com/question/32148386
#SPJ11
A spinner and 4 cards are shown below:
A spinner with 5 equal sectors is shown in the figure. The colors Green, Blue, Purple, Yellow, and Red are marked on it. The arrow points at the purple color. Four cards are shown on the right side. The colors Red, Yellow, Blue, and Pink are marked on them.
Jane spins the spinner and selects a card without looking. What is the probability that the spinner stops at purple and a pink card is selected?
1 over 20
1 over 5
1 over 4
9 over 20
Answers
Answer:
1 over 20
Step-by-step explanation:
Given that:
a spinner and 4 cards
A Spinner ⇒ 5 equal sectors;Color: Blue,Purple,Yellow,Red,Green
Arrow point at purple
Four cards ⇒ Color : Red,Yellow,Blue,Pink
Jane spins the spinner & selects card without looking.
To Find - Probability spinner stops at purple & select pink card.
Solve:
Multiply 4 (the number of cards) with 5 (The number of equal sectors)
\(\frac{1}{5}\times\frac{1}{4}=\frac{1}{20}\) {1 × 1 = 1} {5×4=20}
~lenvy~
Answer:
1 over 20
Step-by-step explanation:
Given the following:
1 spinner and 4 cards
A Spinner which has 5 equal sectors;Color: Green, Blue,Purple,Yellow,Red.
{Arrow point at purple}
Four cards ⇒ which color are Red,Yellow,Blue,Pink
Jane spins the spinner & selects card without looking.
To Find → Probability spinner stops at purple & select pink card.
Since, purple and pink only has one in each of Spinner/card
Thus,
Spinner (5 equal sectors - 1/5}
Card {4 cards - 1/4}
1/4 × 1/5 = 1/20
Hence, probability spinner stops at purple & select pink card is [A] 1/20
[RevyBreeze]
Write the word sentence as an equation. Then solve.
The sum of a number y and −3 is −8.
Equation:_______________
Solution: y=_______
Answers
Answer:
-3y = -8 then you get your answer from that
Step-by-step explanation:
-3y = -8
-3. -3Which expression is equivalent to
(5x³)(4x) ³2
Answers
Answer:
640\(x^{6}\)
Step-by-step explanation:
(5x³)(4x) ³2
(4x) ³ is the same as
4³ * x³ = 64x³
--
(5x³)(64x³)2
5*64*2 = 640
x³ * x³ = \(x^{6}\)
640\(x^{6}\)
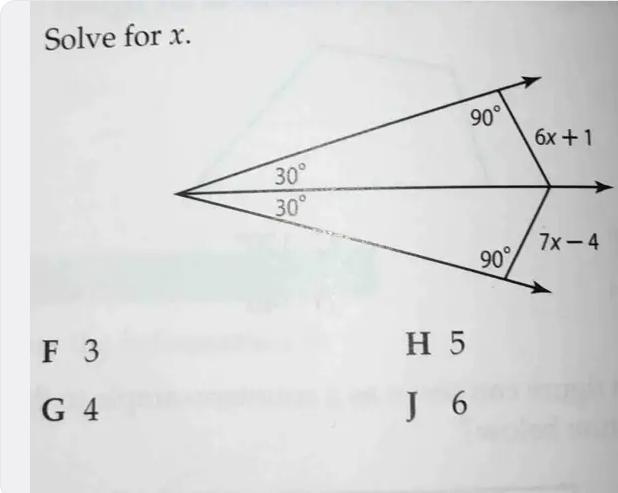
Read question. Then fill in the correct answer on the answer document provided by your teacher or on a sheet of paper.
Solve for x .
F. 3
G. 4
H. 5
J. 6
Answers
The correct option is H. 5. The value of x is 5, which satisfies the given conditions for the congruent triangles Δ ABC and Δ ADC
To solve for x in the given scenario, where two adjacent right-angled triangles label it as Δ ABC and Δ ACD are given with certain angle and side measures, we can utilize the concept of congruent triangles.
Given that ∠ ABC = ∠ CDA = 90°, ∠ BAC = ∠ CAD = 30°, and AC is the common hypotenuse for both triangles, we are also provided with the lengths of BC and CD as BC = 6x + 1 and CD = 7x - 4, respectively.
Consider Δ ABC and Δ ACD ,
∠ ABC = ∠ CDA = 90°(A),
AC is common side(S)
∠ BAC = ∠ CAD = 30°(A)
Δ ABC ≅ Δ ADC (ASA)
That implies, BC = CD (Corresponding parts of congruent triangles)
Since Δ ABC ≅ Δ ADC, we can equate their corresponding sides. Specifically, we can equate BC with CD.
This gives us the equation 6x + 1 = 7x - 4.
To solve for x, we can start by isolating the x terms on one side of the equation.
Adding 4 to both sides, we have ,
6x + 5 = 7x.
Next, subtracting 6x from both sides, we get
5 = x.
Therefore, x is equal to 5.
By substituting x = 5 back into the given expressions for BC and CD, we find that:
BC = 6(5) + 1 = 31 and CD = 7(5) - 4 = 31.
This confirms that the lengths of BC and CD are indeed equal, as expected for congruent triangles.
In conclusion, by solving the equation 6x + 1 = 7x - 4 and isolating x, we find that x = 5. This value satisfies the given conditions and demonstrates that the triangles ABC and ADC are congruent.
Learn more about congruent triangles here:
https://brainly.com/question/30097377
#SPJ4
Plzzzzzzzzzzz helppppppppppp

Answers
Step-by-step explanation:
It’s in step one.
Ling subtracted 6.2 to get rid of it on both side but instead they subtracted it from the right side but added it to the left side when Ling was supposed to subtract from both sides.
expand (5x/4 + 3/4)^3
Answers
Answer:
125x^3 + 27/ 64
Step-by-step explanation :
This can be done in man ways. But I recommend solving what is inside the brackets first.
So add 5x/4 and 3/4, which gives 5x+3/4
Now, rewrite the term with simplified brackets
(5x+3/4)^3
Now we have to cube 5x+3/4
5x+3/4^3 = 125x^3 + 27/64
Hope this helps
Please mark brainiest
A researcher interviews 6 widows about their marriages and notices how many cats are wandering around. Is there a significant relationship between the number of times an old widow was married and the number of cats the old lady owns? ( You don't need to do the math to calculate it - the Pearson r is given).
Times Married: 1 1 2 2 3 3
Cats Owned: 3 2 4 5 5 6
Pearson r = +.91
Write up the conclusion for this study in APA format and be sure to include the r2.
Answers
There is a significant relationship between the number of cats she owns and the number of times an old widow was married (r = +0.91, p < 0.05, r² = 0.82).
Given, the Pearson correlation coefficient of +0.91,
There appears to be a strong +ve correlation between the number of cats she owns and the number of times an old widow was married.
It suggests that the more times a widow was married,the more cats she tends to own.
Approximately 82% of the variance in the number of cats owned can be explained by the number of times a widow was married is indicated by the coefficient of determination (r²).
Hence, we can say that there is a significant relationship between the number of cats she owns and the number of times an old widow was married (r = +0.91, p < 0.05, r² = 0.82).
Learn more about Pearson correlation coefficient here,
https://brainly.com/question/31801929
#SPJ4
given this information, in order to use her 4 hours of time spent studying to get the highest possible test score, how many hours should she have spent solving multiple choice problems, and how many hours should she have spent reviewing lecture notes? 0 hours working on problems, 4 hours reading 2 hours working on problems, 2 hours reading 3 hours working on problems, 1 hour reading 4 hours working on problems, 0 hours reading
Answers
The most effective way to use her 4 hours of study time to get the highest possibility or probability of test scores would be to spend 4 hours working on multiple-choice problems and 0 hours reviewing lecture notes.
From the information given, it is clear that working on multiple-choice problems is the most effective way to improve her test score. Therefore, the highest possibility or probability of test scores would be achieved by spending the most time working on multiple-choice problems.
The available time for studying is 4 hours, so the maximum time that can be spent working on multiple-choice problems is 4 hours. If she spends 4 hours working on multiple-choice problems, she will not have any time left to review lecture notes.
So, the most effective way to use her 4 hours of study time to get the highest possible test score would be to spend 4 hours working on multiple-choice problems and 0 hours reviewing lecture notes.
To learn more about the probability, visit:
brainly.com/question/30034780
#SPJ4
In reviewing retirement portfolios, Kim determined the probability of a client owning stock is 0.80 and the probability of owning a bond is 0.40. The probability of a customer who owns bonds already owning stock is 0.55. What is the probability a client owns both securities in their retirement portfolio
Answers
The probability that a client owns both stocks and bonds in their retirement portfolio is 0.22.
We know the formula for the probability of the intersection of two events,
P(A and B) = P(A) x P(B|A)
Where P(A) is the probability of event A,
And P(B|A) is the conditional probability of event B given that event A has occurred.
In this case,
We want to find the probability that a client owns both stocks and bonds, so we can let,
A = owning stocks B = owning bonds
According to the problem statement,
P(A) = 0.80 (the probability of owning stocks)
P(B) = 0.40 (the probability of owning bonds)
P(A and B|B) = 0.55 (the probability of owning stocks given that the client already owns bonds)
Using the formula, we can calculate the probability of owning both stocks and bonds as,
⇒ P(A and B) = P(B) x P(A and B|B)
= 0.40 x 0.55
= 0.22
Therefore, The probability that a client owns both stocks and bonds in their retirement portfolio is 0.22 or 22%.
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ4
An elevator ascends, or goes up, at a rate of 750 feet per minute. Is the height to which the elevator ascends proportional to the number of minutes it takes to get there?
Answers
Answer:
Yes
Step-by-step explanation:
We know this because the proportion can be used to find another answer.
Example:
How many feet did the elevator ascend in 0.25 minutes?
750 x
---------- = ----------
1 0.25
750(0.25) = 1x
187.5 = x
***Sorry about the format. Hope this helps!
simple random sampling can be described as following: multiple choice none of the above it requires that a defined target population be ordered in some way, usually in the form of a customer list, taxpayer roll, or membership roster. it produces unbiased estimates of a target population's characteristics. compared with systematic random sampling, it is less costly because it can be done relatively quickly. it eliminates the need to identify all sampling uni
Answers
The statement true about simple random sampling is that it produces unbiased estimates of a target population's characteristics. (Option A)
A simple random sampling refers to a type of probability sampling where the researcher randomly selects a population subset from the finite target population in a manner that each member of the population has an equal chance of selection. Data is obtained from the random subset to analyze and draw conclusion about the population. As the participants are randomly selected and have equal chances of selection, the advantage of this type of sampling is the production of unbiased estimates of a target population's characteristics.
Note: The question is incomplete. The complete question probably is: Which of the following is true of simple random sampling? A. It produces unbiased estimates of a target population's characteristics. B. It eliminates the need to identify all sampling units. C. It is less costly when compared to systematic random sampling because it can be done quickly. D. It requires that a defined target population be ordered in some way, usually in the form of a customer list, taxpayer roll, or membership roster. E. It does not require the sampling units to be given any special code prior to drawing a sample unlike systematic random sampling.
Learn more about Simple random sampling:
https://brainly.com/question/27795261
#SPJ4
The number of chickens reared by Chalerm, Kan and Wach is in the ratio 4:3 :5. The total number of chickens is 660. Kan sells 50 of his chickens to Chalerm and 25 chickens to Wach. After this sale, what is the ratio of Chalerm's, Kan's and Wach's chickens?
Answers
After the sale of the chickens from Kan, the ratio of Chalerm's, Kan's and Wach's chickens is 220 : 105 : 275.
We are given that the ratio of the number of chickens reared by Chalerm, Kan and Wach is 4:3:5. We can represent this as:Chalerm's chickens : Kan's chickens : Wach's chickens = 4x : 3x : 5x
We know that the total number of chickens is 660. So we can set up an equation to solve for x:4x + 3x + 5x = 660
12x = 660x = 55
Now we know that the number of chickens reared by Chalerm, Kan, and Wach are:Chalerm's chickens = 4x = 4(55) = 220
Kan's chickens = 3x = 3(55) = 165 Wach's chickens = 5x = 5(55) = 275Kan sells 50 of his chickens to Chalerm and 25 chickens to Wach.
After the sale, Chalerm will have 220 + 50 = 270 chickens, and Wach will have 275 + 25 = 300 chickens.
The new ratio of Chalerm's, Kan's and Wach's chickens after the sale is:Chalerm's chickens : Kan's chickens : Wach's chickens = 270 : 165 : 300
Simplifying this ratio by dividing by 15, we get:Chalerm's chickens : Kan's chickens : Wach's chickens = 18 : 11 : 20
Therefore, after the sale of the chickens from Kan, the ratio of Chalerm's, Kan's and Wach's chickens is 18:11:20.
Given that the ratio of the number of chickens reared by Chalerm, Kan and Wach is 4:3:5. Thus, Chalerm has 4x chickens, Kan has 3x chickens and Wach has 5x chickens, where x is some positive constant. The total number of chickens is 660.
Hence,4x + 3x + 5x = 66012x = 660x = 55Chalerm has 4x = 4 × 55 = 220 chickens.Kan has 3x = 3 × 55 = 165 chickens.
Wach has 5x = 5 × 55 = 275 chickens.
Kan sells 50 chickens to Chalerm, so Chalerm has 220 + 50 = 270 chickens.Kan also sells 25 chickens to Wach, so Wach has 275 + 25 = 300 chickens.
So, the ratio of Chalerm's, Kan's and Wach's chickens after the sale is270:165:300 = 18:11:20
Therefore, the ratio of Chalerm's, Kan's and Wach's chickens after the sale is 18:11:20.
To know more about ratio visit :-
https://brainly.com/question/13419413
#SPJ11
please solve!! 2(x+1)=x-7
Answers
Answer: Solution
=
−
9
Step-by-step explanation:
Answer:
answer is x = -9
Step-by-step explanation:
2x+2=x-7
x= -9
PLLLLLEASE I NEEED HELP

Answers
Answer:
-3/(b-6) = 3/(-b+6) = 3/(6-b)
Step-by-step explanation:
7/(b-6) + 10/(6-b)
= 7/(b-6) + 10/(-b+6)
= 7-10/(b-6)
= -3/(b-6) = 3/(-b+6) = 3/(6-b)
\( {\qquad\qquad\huge\underline{{\sf Answer}}} \)
Let's solve ~
\(\qquad \sf \dashrightarrow \: \cfrac{7}{b - 6} + \cfrac{10}{6 - b} \)
\(\qquad \sf \dashrightarrow \: \cfrac{7}{b - 6} + \cfrac{10}{ - (b - 6)} \)
\(\qquad \sf \dashrightarrow \: \cfrac{7}{b - 6} - \cfrac{10}{ b - 6} \)
\(\qquad \sf \dashrightarrow \: \cfrac{ - 3}{ b - 6}\:\:\: or \:\:\: \dfrac{3}{6-b} \)
In the accompanying diagram,
AIHT WALK).
IF IH = 6, JH = 2,
and
Kj?
LK = 9, what is the length of
O
4
L
O
ON
O
3
H
CLEAR ALL
K

Answers
^congruence concept^
ok. i already answer it

(L2) A circle that contains a polygon so that it passes through each vertex of the polygon is a(n) _____ circle.
Answers
(L2) An inscribed circle is one that encompasses a polygon so that it passes by each of the polygon's vertices.
A circumcircle, not an inscribed circle, is a circle that encircles a polygon at each vertex. A circle that is enclosed within a polygon and intersects each side of the polygon exactly once is said to be inscribed. A circumcircle, on the other hand, is a circle that goes through every vertex of the polygon, with its center located at the point where the perpendicular bisectors of the polygon's sides converge. The greatest circle that can be drawn within a polygon is the circumcircle, while the largest circle that can be drawn inside a triangle is the inscribed circle.
Learn more about polygon
https://brainly.com/question/24464711
#SPJ4
The total cost of buying "n" hamburgers can be represented by the expression 2.75n
How much would purchasing 10 hamburgers (n=10) cost?
Answers
pls help im stuck in this question

Answers
Based on the number of members and the ratio in which they chose the types of film, the number who chose Action in the second week more than the first week is 6 people.
How many chose Action more in the second week?Assuming that the number of members is 99 members, the number who chose Action on the second week were:
= (7 / (5 + 7 + 6)) x 99
= 39 people
The number who chose Action in the first week:
= (5 / (2 + 5 + 8)) x 99
= 33
The difference is:
= 39 - 33
= 6 people
Find out more on ratios at https://brainly.com/question/12024093
#SPJ1
What is the volume of the triangular pyramid? Round to the nearest tenth if
necessary

Answers
Answer: 224m^3
Step-by-step explanation:
Since V=B(Base)h(Height)
B=1/2x4x8
8x4=32x1/2=16
V=16h
H=14
V=16(14)=224
So your answer is 224m^3
(^3 means cubed)
I hope this helps!
Use substitution method y = x - 1 4x + 8 = y
Answers
Answer:
x=-3
y=-4
Step-by-step explanation:
Given:
y=x-1
4x+8=y
Plug in the 1st equation into the 2nd equation
4x+8=x-1
subtract x from both sides
3x+8=-1
subtract 8 from both sides
3x=-9
divide both sides by 3
x=-3
Now that we have the x value, plug it into the first equation:
y=-3-1
simplify
y=-4
So, x=-3, and y=-4.
Hope this helps! :)
Find the volume of the solid obtained by rotating the region enclosed by the graphs x=y^4 and x= y^1/4 about the y-axis over the interval [0,1].
Answers
The volume of the solid obtained by rotating the region enclosed by the graphs \(x=y^4\) and \(x= y^1/4\) about the y-axis over the interval [0,1] is 4π/7.
\(V = π ∫y^4 - y^1/4 dy\)
= π ∫\(y^7/4 dy\)
=\([4π/7*y^(7/4+1)]_0^1\)
= \(4π/7\)
To find the volume of the solid obtained by rotating the region enclosed by the graphs\(x=y^4\) and \(x= y^1/4\) about the y-axis over the interval [0,1], we first use the formula for the volume of a solid of revolution: V = π ∫\(y^2 - y^1/4 dy.\) Then, we rewrite the upper limit of the integral as \(y^7/4\)and evaluate the integral from 0 to 1. This gives us the volume as 4π/7.
The volume of the solid obtained by rotating the region enclosed by the graphs \(x=y^4\) and \(x= y^1/4\) about the y-axis over the interval [0,1] is 4π/7.
Learn more about volume here
https://brainly.com/question/16134180
#SPJ4
If you want to identify the mode of a set of data, which of the following graphical displays is best?
Answers
Answer:
Histogram (Please tell me if you disagree, Have a great day:)
