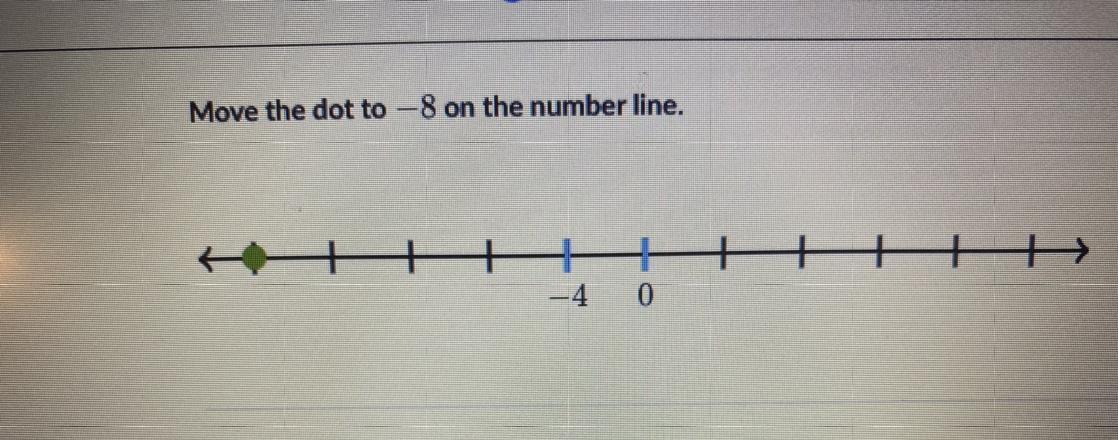
Answers
Answer:
where the green circle is where it goes
Related Questions
big box have 1/4 of 20
gigabytes of ram
Answers
Big boxes have 1/4 of 20 gigabytes of ram will be 5 gigabytes.
What is Algebra?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This approach is used to answer the problem correctly and completely.
Big boxes have 1/4 of 20 gigabytes of ram.
Then the multiplication of the numbers 1/4 and 20 will be given by putting a cross sign between them. Then we have
⇒ (1/4) x 20
⇒ 20 / 4
⇒ 5 gigabytes
Big boxes have 1/4 of 20 gigabytes of ram will be 5 gigabytes.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ1
A triangular window is above the door to a café. The base of the window is 12 feet, and the height is 10 feet.
What is the area of the window?
Enter your answer in the box.
Answers
the answer is 120 just do 10*12
Answer:
The answer is 60.
Step-by-step explanation:
We are doing a triangle not a square, so divide 10*12 in half. What do you get? 60. That's your answer.
Elise is sewing doll blankets to sell at a craft fair. She has 25 full spools of thread in her new sewing kit, and she needs 0.2 spools of thread for each doll blanket she sews. If Elise makes 9 blankets, how many spools of thread will remain?
Answers
Answer: 23 spools of thread
Step-by-step explanation:
0.2 times 9 = 1.8 spools of thread
25 - 1.8 = 23.2 spools of thread
What number is 12% of 45?
Answers
By solving a simple product we will see that 12% of 45 is equal to 5.4
What number is 12% of 45?
If we have a number N and we want to take a percentage P of that number, the operation we need to do is:
new number = N*(P/100%)
Here the original number is N = 45 and the percentage is 12%, then we need to solve:
new number = 45*(12%/100%) = 5.4
Then the 12% of 45 is equal to 5.4
Learn more about percentages:
https://brainly.com/question/843074
#SPJ1
Find a vector function r(t), that represents the curve of intersection of the two surfaces. the cylinder x2 y2=36 and the surface z=4xy
Answers
Given:
\(\begin{aligned}&x^2+y^2=16 \\&z=x y\end{aligned}\)
Express 16 as \(4^{2}\): \(x^2+y^2=16\)
\(x^2+y^2=4^2\\x^2+y^2=4^2 \times 1\)
Trignometry,
\(\cos ^2(t)+\sin ^2(t)=1\)
Now, substitute \(\cos ^2(t)+\sin ^2(t)\) for 1:
\(\begin{aligned}&x^2+y^2=4^2 \times 1 \\&x^2+y^2=4^2 \times\left[\cos ^2(t)+\sin ^2(t)\right]\end{aligned}\\x^2+y^2=4^2 \times \cos ^2(t)+4^2 \times \sin ^2(t)\)
Law of indicates:
\(\begin{aligned}&x^2+y^2=[4 \times \cos (t)]^2+[4 \times \sin (t)]^2 \\&x^2+y^2=[4 \cos (t)]^2+[4 \sin (t)]^2\end{aligned}\\x^2=[4 \cos (t)]^2 \text { and } y^2=[4 \sin (t)]^2\)
Taking positive square roots as follows:
\(x=4 \cos (t), y=4 \sin (t)\)
Recall that, z = xy.
Now, we have:
\(\begin{aligned}&z=4 \cos (t) \times 4 \sin (t) \\&z=16 \cos (t) \cdot \sin (t)\end{aligned}\)
Now, substitute the values:
\(r(t)=x_t i+y_t j+z_t k\)
So, the vector r(t) is: \(r(t)=(4 \cos (t)) i+(4 \sin (t)) i+(16 \cos (t) \cdot \sin (t)) i\)
Therefore, the vector function r(t) is written as: \(r(t)=x_t i+y_t j+z_t k\)
Know more about vector functions here:
https://brainly.com/question/14895420
#SPJ4
IM GIVING BRAINLIEST!!!PLEASE HELP!!!

Answers
Answer:
C (-1/2, -4 1/2)
Step-by-step explanation:
x = -2/(2·2)
x = -2/4 or -1/2
y = 2(-1/2)² + 2(-1/2) - 4
y = 2(1/4) - 1 - 4
y = 1/2 - 1 - 4 or -1/2 - 4 which equals -4 1/2
Help me I’m dumb , I feel as if I’m right but I ain’t sure.

Answers
Answer:don’t worry u not dum and also im sorry that’s not a function.
Step-by-step explanation:
Give me brainliest!
If lisa spends her income on veggie burgers and pints of soy milk and the price of veggie burgers is three times the price of a pint of soy milk, then when lisa maximizes her utility she will buy?
Answers
If Lisa spends her income on veggie burgers and pints of soy milk and the price of veggie burgers is three times the price of a pint of soy milk, then when Lisa maximizes her utility she will buy both goods until the marginal utility of veggie burgers is three times the marginal utility of soy milk.
What is marginal utility?In economics, utility is defined as the satisfaction or benefit gained from using a product. The marginal utility of a good or service describes how much pleasure or satisfaction consumers gain as a result of a one-unit increase or decrease in consumption. There are three different kinds of marginal utility. They have a marginal utility of either positive, negative, or zero. For example, if Lisa spends her money on veggie burgers and pints of soy milk, and the price of the veggie burgers is three times the price of the soy milk, Lisa will maximize her utility by purchasing both goods until the marginal utility of the veggie burgers is three times the marginal utility of the soy milk.Therefore, if Lisa spends her income on veggie burgers and pints of soy milk and the price of veggie burgers is three times the price of a pint of soy milk, then when Lisa maximizes her utility she will buy both goods until the marginal utility of veggie burgers is three times the marginal utility of soy milk.
Know more about marginal utility here:
https://brainly.com/question/15050855
#SPJ4
"1.If you save 300.00 per month at an annual rate of 3.5% for 15
years and then start saving 650.00 a month for another 15 years at
an annual rate of 6.5%, how much will you have at the end of the
third year?
Answers
The total savings at the end of the third year will be approximately \(\$417,060.15\).
To calculate the total amount saved at the end of the third year, we need to determine the savings accumulated during each period and then sum them.
In the first 15 years, with a monthly savings of \(\$300\)and an annual interest rate of \(3.5\%\), we can use the future value of an ordinary annuity formula:
\(\[A = P \times \left(\frac{(1 + r)^n - 1}{r}\right)\]\)
where:
- \(A\)is the accumulated savings
- \(P\) is the monthly savings amount
- \(r\) is the monthly interest rate (\(3.5\% / 12\))
- \(n\) is the total number of months (15 years x 12 months/year)
Calculating the first 15-year savings:
\(\[A_1 = 300 \times \left(\frac{(1 + \frac{0.035}{12})^{15 \times 12} - 1}{\frac{0.035}{12}}\right)\]\)
In the next 15 years, with a monthly savings of \(\$650\) and an annual interest rate of \(6.5\%\), we can use the same formula:
Calculating the next 15-year savings:
\(\[A_2 = 650 \times \left(\frac{(1 + \frac{0.065}{12})^{15 \times 12} - 1}{\frac{0.065}{12}}\right)\]\)
Finally, to find the total savings at the end of the third year, we sum the accumulated savings from the first and second periods:
\(\[A_{\text{total}} = A_1 + A_2\]\)
To calculate the total savings at the end of the third year, we first need to find the accumulated savings for the two periods.
Calculating the accumulated savings for the first 15 years:
\(\(A_1 = 300 \times \left(\frac{{(1 + \frac{{0.035}}{{12}})^{{15 \times 12}} - 1}}{{\frac{{0.035}}{{12}}}}\right) \approx 68,081.80\)\)
Calculating the accumulated savings for the next 15 years:
\(\(A_2 = 650 \times \left(\frac{{(1 + \frac{{0.065}}{{12}})^{{15 \times 12}} - 1}}{{\frac{{0.065}}{{12}}}}\right) \approx 348,978.35\)\)
Now, we can find the total savings at the end of the third year:
\(\(A_{\text{{total}}} = A_1 + A_2 \approx 68,081.80 + 348,978.35 = 417,060.15\)\)
Therefore, the total savings at the end of the third year will be approximately \(\$417,060.15\).
Learn more about annuity formula
https://brainly.com/question/33002081
#SPJ11
If you Saving $300/month for 15 years at 3.5%, then $650/month for another 15 years at 6.5%, will yield approximately $21,628.59 after three years.
To calculate the total amount you will have at the end of the third year, we can follow these steps:
1. Calculate the future value of the first saving period:
Using the formula for compound interest:
\(\[ \text{Future Value} = P \times \frac{{(1 + r)^t - 1}}{r} \]\)
Where:
\(\( P \)\) = Monthly savings amount
\(\( r \)\) = Annual interest rate (as a decimal)
\(\( t \)\) = Time period in years
For the first saving period:
\(\( P = \$300.00 \)\)
\(\( r = 0.035 \)\) (3.5% annual interest rate)
\(\( t = 15 \)\) (years)
Future Value of the first saving period:
\(\[ \text{Future Value} = \$300.00 \times \frac{{(1 + 0.035)^{15} - 1}}{0.035} \]\)
2. Calculate the future value of the second saving period:
For the second saving period:
\(\( P = \$650.00 \)\)
\(\( r = 0.065 \)\) (6.5% annual interest rate)
\(\( t = 15 - 3 = 12 \)\) (remaining years after the first saving period)
Future Value of the second saving period:
\(\[ \text{Future Value} = \$650.00 \times \frac{{(1 + 0.065)^{12} - 1}}{0.065} \]\)
3. Calculate the total future value at the end of the third year:
Total Future Value = Future Value of the first saving period + Future Value of the second saving period
The calculations for the total amount you will have at the end of the third year are as follows:
Future Value of the first saving period:
\(\[ \text{Future Value of the first saving period}\) = \(\$300.00 \times \frac{{(1 + 0.035)^{15} - 1}}{{0.035}} \approx \$7,648.63\)
Future Value of the second saving period:
\(\[ \text{Future Value of the second saving period}\) = \(\$650.00 \times \frac{{(1 + 0.065)^{12} - 1}}{{0.065}} \approx \$13,979.96\)
Total Future Value at the end of the third year:
\(\[ \text{Total Future Value}\) = \(\text{Future Value of the first saving period} + \text{Future Value of the second saving period}\)
\(\[ \approx \$7,648.63 + \$13,979.96 \approx \$21,628.59 \]\)
Therefore, If you Saving $300/month for 15 years at 3.5%, then $650/month for another 15 years at 6.5%, will yield approximately $21,628.59 after three years.
To know more about Saving visit -
brainly.com/question/17440040
#SPJ11
Can someone really help me :(
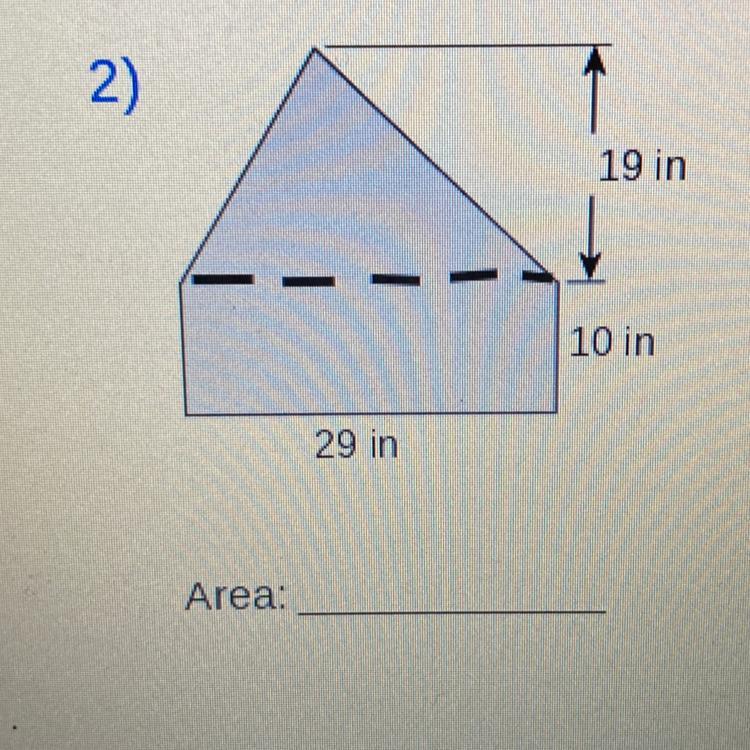
Answers
Area of triangle:
A= 1/2*b*h
= 1/2 *(29)* (19)
= 1/2 *(551)
= 275.5 in^2
Area of rectangle:
A= l * w
= (29) * (10)
= 290 in^2
Total Area:
275.5 + 290 = 565.5 in^2
Hope this helps! Have a great day :)
Answer:
565.5 in
Step-by-step explanation:
The area for a rectangle is A = lw
So A = (29)(10)
A = 290
The area for a triangle is A = 1/2bh
So A = 1/2(29)(19)
A = 1/2(551)
A = 275.5
You combine the two numbers to get a total area of 565.5 in
Write the equation of the circle that passes through the point (-4,-3) and has a center at (-8, -6).
Answers
The equation of the circle that passes through the point (-4,-3) and has a center at (-8, -6) is \((x + 8)^2 + (y + 6)^2 = 25\). The equation is in standard form, where the center and radius of the circle is (-8, -6), 5 units.
The equation of a circle with center (a, b) and radius r is given by:
\((x - a)^2 + (y - b)^2 = r^2\)
In this problem, we are given that the center of the circle is (-8, -6), so we can substitute these values for a and b in the equation:
\((x - (-8))^2 + (y - (-6))^2 = r^2\)
\((x + 8)^2 + (y + 6)^2 = r^2\)
The distance between two points (x1, y1) and (x2, y2) is given by the distance formula:
\(d = sqrt((x2 - x1)^2 + (y2 - y1)^2)\)
\(d = sqrt((x2 - x1)^2 + (y2 - y1)^2)\)
\(d = sqrt((4)^2 + (3)^2)\)
d = 5
Therefore, the radius of the circle is 5.
\((x + 8)^2 + (y + 6)^2 = 5^2\)
\((x + 8)^2 + (y + 6)^2 = 25\)
So the equation of the circle that passes through the point (-4, -3) and has a center at (-8, -6) is: \((x + 8)^2 + (y + 6)^2 = 25\)
To learn more about circle please click on below link
https://brainly.com/question/17357009
#SPJ1
There is a quadrilateral MNPQ in which side MN is congruent to side PQ and side NP is parallel to side MQ. The diagonal MP and the diagonal NQ intersect each other at point R. If MP = 6x − 5, QR = 3x + 1, and RN = 6, what is QN?
Answers
Answer: QN = 12
Step-by-step explanation: This quadrilateral is a paralelogram because its 2 opposite sides (NP and MQ) are parallel and the other 2 (MN and PQ) are congruent.
In paralelogram, diagonals bisect each other, which means QR = RN.
If QR = RN:
QR = 6
Then,
QN = QR + RN
QN = 6 + 6
QN = 12
The diagonal QN of quadrilateral MNPQ is QN = 12.
The sum of 3 and c is less than or equal to -23.
Answers
Answer:
c≤−26
hope that helped <3
URGENT !!!!!!!!! Please answer correctly !!!!! Will be marking Brianliest !!!!!!!!!!!!!!!!

Answers
Step by Step :
18 - 8 = 10
-15 - 10 = -25
10/-25 = -2/5
Find the indicated term in the sequence.
Please show steps too! Thank you.

Answers
Answer:
Value of An if n is 17 = -834
Step-by-step explanation:
Given:
A100 = 245
d = 13
n = 17
Find:
Value of An if n = 17
Computation:
An = a + (n-1)d
A100 = a + (100-1)13
245 = a + (99)17
245 = a + 1,287
a = 245 - 1,287
a = -1,042
So,
Value of An if n = 17
An = a + (n-1)d
A17 = -1,042 + (17-1)(13)
A17 = -1,042 + (16)(13)
A17 = -1,042 + 208
A17 = -834
Value of An if n is 17 = -834
If Gina tosses the coins 40 times, what is the
approximate relative frequency that she
will get 2 heads?
Answers
Answer:
20 times
Step-by-step explanation:
40 / 2 = 20?? sorry if im wrong
Answer the following questions for the function
f(x) = x sqrt(x^2 + 36) defined on the interval - 5 ≤ r ≤ 6. F(x) is concave down on the interval x = to x =
f(x) is concave up on the interval x = to x = The inflection point for this function is at x = The minimum for this function occurs at x = The maximum for this function occurs at x =
Answers
f(x) is concave down on the interval -5 ≤ x ≤ -6 and 0 ≤ x ≤ 6.
f(x) is concave up on the interval -6 ≤ x ≤ 0.
To determine where f(x) is concave up or concave down, we need to calculate the second derivative of f(x):
f(x) = x √(\(x^2\) + 36)
f'(x) = √\(x^2\) + 36) + \(x^2\) √(\(x^2\) + 36)
f''(x) = (x (\(x^2\) +72) )/((\(x^2\)+36)\(^(3\)/2))
To find where f(x) is concave up or concave down, we need to find where f''(x) > 0 (concave up) or f''(x) < 0 (concave down).
f''(x) = 0 when x = 0 or x = +/-6.
Thus, f(x) is concave down on the interval -5 ≤ x ≤ -6 and 0 ≤ x ≤ 6, and concave up on the interval -6 ≤ x ≤ 0.
The inflection point for this function is at x = 0.
To find the minimum and maximum for this function, we need to look at the endpoints and critical points of the interval -5 ≤ x ≤ 6.
f(-5) = -5√61 and f(6) = 6√72, so the minimum occurs at x = -5 and the maximum occurs at x = 6.
Therefore:
f(x) is concave down on the interval -5 ≤ x ≤ -6 and 0 ≤ x ≤ 6.
f(x) is concave up on the interval -6 ≤ x ≤ 0.
The inflection point for this function is at x = 0.
The minimum for this function occurs at x = -5.
The maximum for this function occurs at x = 6.
To know more about inflection point, here
https://brainly.com/question/25918847
#SPJ4
PLS ANSWER ASAP ILL MARK BRAINLIEST

Answers
Answer:
4
Step-by-step explanation:
g=4
that means
16/g= 16/4
16/4=4
A container has 3 3/8
pounds of flour.
Mr. Wright gives each member of his cooking class 3/16
pound of flour, which empties the container.
How many people are in Mr. Wright’s class?
Answers
Answer:
18
Step-by-step explanation:
3=48/16
48/16 + 3/8 (6/16) = 54/16
54÷3=18
answer is 18 students
\(4 3/8 + 2 5/12 -3 1/6\)
Answers
55/24 will be the simplified form of the expression 43/8 + 25/12 -31/6.
What is Fraction?An element of a whole is a fraction. The number is represented mathematically as a quotient, where the numerator and denominator are split. Both are integers in a simple fraction. A fraction appears in the numerator or denominator of a complex fraction. The numerator of a correct fraction is smaller than the denominator.
given an expression 43/8 + 25/12 -31/6
Simplify given data
=> 43/8 + 25/12 -31/6
=> 5 + 3/8 + 2 + 1/12 - 5 - 1/6
=> 2 + 3/8 + 1/12 - 2/12
=> 2 + 3/8 -1/12
=> 2 + 9/24 -2/24
=> 2 + 7/24
=> 55/24
therefore, The simplified form of the given equation will be 55/24.
Learn more about fractions here:
https://brainly.com/question/10354322
#SPJ1
given the following weights for a linear regression model (not linear classifier) w0=6, w1=9, w2=2, w3=10 what will hw return given the input vector < 3, 1, 5 >?
Answers
The return value of the given linear regression model with weights containing an input vector < 3, 1, 5 > is 85
To find the output of the given linear regression model with weights w0=6, w1=9, w2=2, and w3=10 for the input vector <3, 1, 5>,
follow these steps:
1. Multiply each input value by its corresponding weight: (3 * w1) + (1 * w2) + (5 * w3)
2. Add the result from step 1 to the bias term, w0.
Let's calculate:
Step 1: (3 * 9) + (1 * 2) + (5 * 10) = 27 + 2 + 50 = 79
Step 2: 79 + 6 = 85
So, the linear regression model will return a value of 85 for the given input vector <3, 1, 5>.
Learn more about the linear regression model: https://brainly.com/question/25987747
#SPJ11
PLEASE HELP ME!!!!!
The coordinates of point A on a grid are (5, −3). Point A is reflected across the x-axis to obtain point B. The coordinates of point B are (5, ___).
Answers
Answer:
the answer is 3
Step-by-step explanation:
At the grocery tore 4 pint of ice cream cot $10. 36. How much would 20 pint of ice cream cot?
Answers
Answer:$51.08
Step-by-step explanation:
what is the maximum volume of an open cylinder with surface area equal to 16pi and a radius between 1 and 8 feet
Answers
The maximum volume of an open cylinder with surface area equal to 16π and a radius between 1 and 8 feet is 16π cubic feet, and it is achieved when the radius is equal to 2 feet and the height is equal to 4 feet.
The surface area of an open cylinder is given by the formula 2πrh + 2πr^2, where r is the radius and h is the height. We are given that the surface area is equal to 16π, so we have the equation:
2πrh + 2πr^2 = 16π
Simplifying this equation, we get:
r(h + r) = 8
We want to maximize the volume of the cylinder, which is given by the formula V = πr^2h. Using the equation we derived above, we can express the height in terms of the radius:
h = (8 - r^2)/r
Substituting this expression for h into the formula for the volume, we get:
V = πr^2((8 - r^2)/r)
Simplifying this expression, we get:
V = 8πr - πr^3
To find the maximum volume, we need to find the value of r that maximizes this expression. To do this, we take the derivative of the expression with respect to r:
dV/dr = 8π - 3πr^2
Setting this equal to zero, we get:
8π - 3πr^2 = 0
Solving for r, we get:
r = 2
We can verify at this is a maximum by taking the second derivative of the expression with respect to r:
d^2V/dr^2 = -6πr
At r = 2, this is negative, indicating that we have a maximum.
Therefore, the maximum volume is achieved when the radius is equal to 2 feet. Substituting this into the equation we derived for h, we get:
h = (8 - 2^2)/2 = 4
So the maximum volume is:
V = π(2)^2(4) = 16π cubic feet.
To learn more about volume here:
brainly.com/question/16134180#
#SPJ11
Which theorem has two sides and a non-included angle?
Answers
Angle-Angle-Side (AAS) Theorem has two sides and a non-included angle.
What is Angle-Angle-Side (AAS) Theorem?The triangles are congruent if two angles and a non-included side in one triangle are congruent with two angles and the corresponding non-included side in another triangle, according to the Angle-Angle-Side (AAS) Congruence Theorem.The side-angle-side (SAS) theorem is the first such theorem. The triangles are congruent if two sides and the included angle of one triangle are equivalent to two sides and the included angle of another triangle.When two angles and an unincluded side of one triangle are equal to two angles and the corresponding unincluded side of the other triangle, two triangles are said to be congruent (AAS=AAS).To learn more about Angle-Angle-Side (AAS) Theorem refer to:
https://brainly.com/question/3168048
#SPJ4
The table shows the distance Shannon ran over a week.
Day
Tuesday
Length {km)
5
2
6
Wednesday
1911 DO NOT
Friday
Saturday
How many more kilometers did Shannon run on Friday than on Saturday?
kilometer
PLEASE HELP

Answers
Answer:
Shannon run 1.5 km more on Friday than on Saturday.
Step-by-step explanation:
From the given table
Distance run on Friday = 4/2 = 2 kmDistance run on Saturday = 1/2 = 0.5 kmIn order to run how many more kilometers Shannon run on Friday than on Saturday, we need to subtract the distance run on Saturday from the distance run on Friday.i.e.
Friday run - Saturday run = 2 - 0.5
= 1.5 km
Thus, Shannon run 1.5 km more on Friday than on Saturday.
A colony of 32 bacteria doubles in every 4 hours. How many bacteria are in the colony after 16 hours?
Answers
The number of bacteria in the colony after 16 hours = 992
Explanation:The bacteria doubles every 4 hours and we are considering 16 hours
The number of times that the bacteria doubles is 16/4 = 4 times
Note that there is a first term and four other terms when the bacteria were doubled
There are 5 terms in total
Number of terms, n = 5
The initial amount of bacteria, a = 32
The bacteria doubles every 4 hours
That is, the common ratio, r = 2
Since there is a common ratio, this is a geometric progression.
The sum of n terms of a geometric progression is given as:
\(S_n=\frac{a(r^n-1)}{r-1}\)Substitute a = 32, r = 2, and n = 5 into the formula above to get the number of bacteria in the colony after 16 hours
\(\begin{gathered} S_4=\frac{32(2^5-1)}{2-1} \\ S_4=\frac{32(32-1)}{1} \\ S_4=32(31) \\ S_4=992 \end{gathered}\)The number of bacteria = 992
Calculate the effective interest on £2000 at 3% interest
quarterly after 4 years.
Answers
The effective interest on £2000 at a 3% interest rate compounded quarterly over a period of 4 years is approximately £245.15.
To calculate the effective interest, we need to use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = the future value of the investment (including interest)
P = the principal amount (initial investment)
r = the annual interest rate (as a decimal)
n = the number of compounding periods per year
t = the number of years
In this case, the principal amount (P) is £2000, the annual interest rate (r) is 3% (or 0.03 as a decimal), the compounding is done quarterly (n = 4), and the investment period (t) is 4 years.
Plugging the values into the formula:
A = £2000(1 + 0.03/4)^(4*4)
= £2000(1 + 0.0075)^16
= £2000(1.0075)^16
≈ £2000(1.126825)
Calculating the future value:
A ≈ £2253.65
To find the effective interest, we subtract the principal amount from the future value:
Effective Interest = £2253.65 - £2000
≈ £253.65
Therefore, the effective interest on £2000 at a 3% interest rate compounded quarterly after 4 years is approximately £253.65.
Learn more about compound interest here:
https://brainly.com/question/22621039
#SPJ11
15 POINTS!!
answer the question in the picture

Answers
Answer:
10, 0, 2.
Step-by-step explanation:
It means that the number is greater than -3.
So, 10, 0, 2, are all greater than -3, and all the other numbers are smaller. So 10, 0, 2 are the numbers that are part of the solution for x>-3.
Answer:
10(a), 0(c), 2(d)
if we are testing for the difference between the mean of two independent populations with samples of n1=20 and n2=20 the number of degrees of freedom is qual to
Answers
df = [(s1^2/n1 + s2^2/n2)^2] / [((s1^2/n1)^2)/(n1 - 1) + ((s2^2/n2)^2)/(n2 - 1)]
where s1 and s2 are the sample standard deviations of the two populations.
Substituting the given values, we get:
df = [(s1^2/20 + s2^2/20)^2] / [((s1^2/20)^2)/19 + ((s2^2/20)^2)/19]
Since the values of s1 and s2 are not given, we cannot compute the value of df. However, in general, the degrees of freedom for a t-test with sample sizes of 20 and equal variances would be 38 (assuming a two-tailed test and a significance level of 0.05).