When -x^2+ 6x + 2 is subtracted from x^2 - 4x + 3, will the result be a polynomial?
Answers
Step-by-step explanation:
x² - 4x + 3 - ( - x² + 6x + 2) = x² - 4x + 3 + x² - 6x - 2
= x² + x² - 4x - 6x + 3 - 2
= 2x² - 10x + 1
Related Questions
please help this is the last question

Answers
Answer:
The median is the same for both car types, but Bandit have lower mean.
Step-by-step explanation:
a student at another business school surveys 100 of 1000 graduates from last year and asks about their salaries. the researcher finds that the average income is $65, 000, with a standard deviation of $8000. if you wanted to be 95% sure that the real mean of all 1000 students is within a range of the sample mean, what would you set your confidence interval lower and upper bounds to be?
Answers
As per the given standard deviation, the confidence interval is 495.84, upper bound is $65,495.8 and the lower bound is $64,504.2
Confidence interval
Confidence interval means a range of values, bounded above and below the statistic's mean, that likely would contain an unknown population parameter.
Given,
A student at another business school surveys 100 of 1000 graduates from last year and asks about their salaries. the researcher finds that the average income is $65, 000, with a standard deviation of $8000.
Here we need to find the confidence interval lower and upper bounds if you wanted to be 95% sure that the real mean of all 1000 students is within a range of the sample mean.
While we looking into the given question, we have identified the following values,
standard deviation = $8,000
Average income = $65,000
Sample size = 1000
Confidence level = 95%
Then the value of confidence interval is calculated by the formula,
Then we get the value of
Lower bound = 64504.2
Upper bound = 65495.8
Confidence interval (±) = 495.84
To know more about Confidence interval here.
https://brainly.com/question/24131141
#SPJ4
can plz tell the to 35÷23
Answers
Answer: 1.5
Step-by-step explanation:
Answer:
1.52173913043
or 1.5%
Step-by-step explanation:
Out of the 13 girls who tried out for the softball team, 10 will be chosen for the team. Find the number of different 10-person teams.
Answers
Using the combination formula, it is found that there are 286 10-person teams.
The order in which the girls are chosen is not important, hence the combination formula is used to solve this question.
What is the combination formula?\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by:
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
In this problem, 10 girls are chosen from a set of 13, hence:
\(C_{13,10} = \frac{13!}{10!3!} = 286\)
There are 286 10-person teams.
More can be learned about the combination formula at https://brainly.com/question/25821700
A map has a scale of cm to 5 m. Two cities or 45 m away. How far apart are they on the map
Answers
if the two cities are 45 meters apart in reality, they would be represented as 5 centimeters apart on the map.
The given scale on the map is "cm to 5 m." This means that every centimeter on the map represents 5 meters in reality.
We are told that the two cities are 45 meters apart in reality. To find out how far apart they are on the map, we need to determine the equivalent distance in centimeters.
Since every centimeter on the map represents 5 meters, we can set up a proportion to find the distance on the map:
(cm on the map) / (5 m in reality) = (x cm on the map) / (45 m in reality)
By cross-multiplying and solving for x, we get:
x cm on the map = (cm on the map) * (45 m in reality) / (5 m in reality)
Simplifying the expression, we have:
x cm on the map = 9 * (cm on the map)
This means that every centimeter on the map represents 9 meters in reality.
Therefore, if the two cities are 45 meters apart in reality, they would be represented as 5 centimeters apart on the map.
Learn more about map here
https://brainly.com/question/27928319
#SPJ11
find the directional derivative of f(x,y,z)=xy z^2, at (3,2,1) in the direction of v⃗ =i⃗ j⃗ k
Answers
The directional derivative of a function f(x, y, z) at a point (a, b, c) in the direction of a vector v⃗ = <v₁, v₂, v₃> is given by the dot product of the gradient of f and the unit vector in the direction of v⃗.
First, let's find the gradient of f(x, y, z):
∇f(x, y, z) = <∂f/∂x, ∂f/∂y, ∂f/∂z>
For f(x, y, z) = xy z², we have:
∂f/∂x = yz²
∂f/∂y = xz²
∂f/∂z = 2xyz
So, the gradient of f(x, y, z) is:
∇f(x, y, z) = <yz², xz², 2xyz>
Now, let's find the unit vector in the direction of v⃗ = <v₁, v₂, v₃>:
|v⃗| = √(v₁² + v₂² + v₃²)
|v⃗| = √(1² + 1² + 1²)
|v⃗| = √3
The unit vector in the direction of v⃗ is:
u⃗ = v⃗ / |v⃗|
u⃗ = <1/√3, 1/√3, 1/√3>
Finally, the directional derivative of f(x, y, z) at (3, 2, 1) in the direction of v⃗ = <i⃗, j⃗, k⃗> is given by:
Dv(f) = ∇f(a, b, c) · u⃗
Dv(f) = ∇f(3, 2, 1) · <1/√3, 1/√3, 1/√3>
Dv(f) = <(yz²)(3) + (xz²)(2) + (2xyz)(1)> · <1/√3, 1/√3, 1/√3>
Dv(f) = <3yz² + 2xz² + 2xyz> · <1/√3, 1/√3, 1/√3>
Therefore, the directional derivative of f(x, y, z) at (3, 2, 1) in the direction of v⃗ = <i⃗, j⃗, k⃗> is 3yz² + 2xz² + 2xyz.
To know more about directional derivative, refer here:
https://brainly.com/question/29451547#
#SPJ11
What is the least common denominator for the fractions 5/6and3/8? A).14 B).18 C).24 D).48

Answers
Answer:
To find the least common denominator, or lcd, you have to find the least common multiple, or lcm. To do that you find the multiples of each number until they equal each other. I set up a chart like this,
6 -
8 -
and then I start listing multiples so,
6 - 6, 12, 18, 24,
8 - 8, 16, 24,
I stop after I find a number they are both equal to. So to get to that number I would multiply 8 by 3, and 6 by 4. This gives me 24 as the lcd. If you need the lcd to add the fractions together, then whatever you did to the bottom do to the top. So 5/6 would become 20/24 and 3/8 would become 9/24.
Answer: 24
Step-by-step explanation:
help!!
A letter is chosen from the word BELIEVABLE Which describes the
probability of randomly choosing a consonant?
Answers
Answer: 1/2
Explanation: There are 5 vowels and 5 consonants in the word believable. So to find the consonant, you have to do a fraction with consonant as numerator and the total number of letters as the denominator. Since there are 5 consonants and 10 letters in total, the simplest form will be 1/2.
What does it mean for a sample to have a standar deviation of zero? describe the scores in such a sample
Answers
Given that sample standard deviation is zero. This indicates that the variance of sample is also zero as square of sample standard deviation is sample Variance. Variance is average of the squared deviations from mean. As shown in below formula
Since Variance = 0 , we substitute in formula and we get the sum of squares of deviations of all data points from mean should be zero. This is only possible if and only if all the data points in the data distribution are same as mean of the data distribution. In the case the variance and standard deviation will be zero.
Variance = Summation n to i = 1 \(\frac{(X_{1-X} )^2}{n-1}\)
0 = Summation n to i = 1\(\frac{(X_{1-X} )^2}{n-1}\)
Summation n to i \({(X_{1-X} )^2\) = 0
Learn more about Variance and Standard Deviation at:
https://brainly.com/question/20251852
#SPJ4
12. DIG DEEPER The sum of a three-digit
number and a one-digit number is 731.
The product of the numbers is 2,908,
What are the numbers?
Answers
The three digit number is 727 while the one digit number is 4
Given data
The sum of a three-digit number and a one-digit number is 731.
The product of the numbers is 2,908
How to solve for the numberslet three digit number be x, y, and z
let the one digit be w
The sum
xyz + w =731
xyz * w = 2,908
making xyz the subject of formula
xyz = 731 - w
plugging in xyz into xyz * w = 2,908
( 731 - w ) * w = 2908
731w - w^2 = 2908
w^2 - 731w + 2908 = 0
solving the quadratic equation gives
w = 727 or 4
since w is a one digit number then w = 4
plugging in w = 4 into xyz + w =731 we have
xyz + w =731
xyz + 4 =731
xyz =731 - 4
xyz = 727
Hence the three digit number is 727 while the one digit number is 4
Read more word problems on here: https://brainly.com/question/13818690
#SPJ1
21. Andre grew a plant for a science experiment. At the end of his
experiment, the plant was 100.8 centimeters tall. Andre calculated
that the plant grew an average of 3.6 centimeters per day since
the start of his experiment. How many days did Andre's
experiment last?
Answers
Answer:
he answer is 140 minutes to plant 14 saplings.
Step-by-step explanation:
30 divided by 3=10
so it takes 10 minutes to plant one sapling.
10x14=140 so this is how you get your answer. im 99% sure
Answer:
100.8÷3.6=28
he grew the plant for 28 days
in the citation 319 n.w. 2d 459, the number 459 represents the
Answers
The number 459 in the citation 319 N.W. 2d 459 represents the page number where the case or legal opinion can be found in the North Western Reporter, Second Series. The North Western Reporter is a series of case reporters that includes court decisions from various states in the northwestern region of the United States.
In legal citations, the number before the "N.W." indicates the volume number of the reporter. So in this case, "319" refers to the specific volume where the case is located. The abbreviation "N.W." stands for North Western Reporter, which is the name of the reporter series. The number "2d" after "N.W." indicates that this is the second series of the North Western Reporter.
To locate the case within the volume, the number "459" refers to the page number where the case begins. This allows readers, such as lawyers, judges, or researchers, to easily find and reference the specific case within the reporter.
In summary, the number "459" in the citation 319 N.W. 2d 459 represents the page number where the case can be found in the North Western Reporter, Second Series.
know more about northwestern region, state.
https://brainly.com/question/749299
#SPJ11
Find the parametric line of intersection between the planes 3x−4y+8z=10 and x−y+3z=5
Answers
To find the parametric line of intersection between the planes, we need to solve the system of equations formed by the two planes. Let's proceed with the solution step-by-step.
Given planes:
1) 3x - 4y + 8z = 10
2) x - y + 3z = 5
Step 1: Solve for one variable in terms of the other two variables in each equation. Let's solve for x in terms of y and z in both equations:
1) 3x - 4y + 8z = 10
3x = 4y - 8z + 10
x = (4y - 8z + 10) / 3
2) x - y + 3z = 5
x = y - 3z + 5
Step 2: Set the expressions for x in both equations equal to each other:
(4y - 8z + 10) / 3 = y - 3z + 5
Step 3: Solve for y in terms of z:
4y - 8z + 10 = 3y - 9z + 15
4y - 3y = 8z - 9z + 15 - 10
y = -z + 5
Step 4: Substitute the value of y back into one of the equations to solve for x:
x = y - 3z + 5
x = (-z + 5) - 3z + 5
x = -4z + 10
Step 5: Parametric representation of the line of intersection:
The line of intersection can be represented parametrically as:
x = -4z + 10
y = -z + 5
z = t
Here, t is a parameter that can take any real value.
So, the parametric line of intersection between the planes 3x - 4y + 8z = 10 and x - y + 3z = 5 is:
x = -4z + 10
y = -z + 5
z = t, where t is a parameter.
To know more about parametric line visit:
https://brainly.com/question/30286426
#SPJ11
x + 3y > –3 and y < One-halfx + 1?
Answers
The complete question is
"Which is the graph of the system x + 3y > –3 and y < One-halfx + 1?"
The solution is the intersection region of all the solutions in the system of inequalities.
What is inequality?Inequality is defined as the relation which makes a non-equal comparison between two given functions.
We know that the lines are given as;
x + 3y = -3
y = 1/2 x + 1
Solving for "y" from the first line;
3y = -3 - x
y = -1 - x/3
For the line x + 3y = -3 the x-intercepts;
y = 0
y = -1 - x/3
0 = -1 - x/3
x/3 = -1
x = -3
And the y-intercept;
y = -1
For the line y = 1/2 x + 1 the x-intercepts;
y = 0
0= 1/2 x + 1
1/2x = -1
x = -2
And the y-intercept
x = 0
y = 1
Now we can graph both lines,
The solution is the intersection region of all the solutions in the system of inequalities.
Learn more about inequality ;
brainly.com/question/14164153
#SPJ1

Answerrrrrr If anyone knows just reply
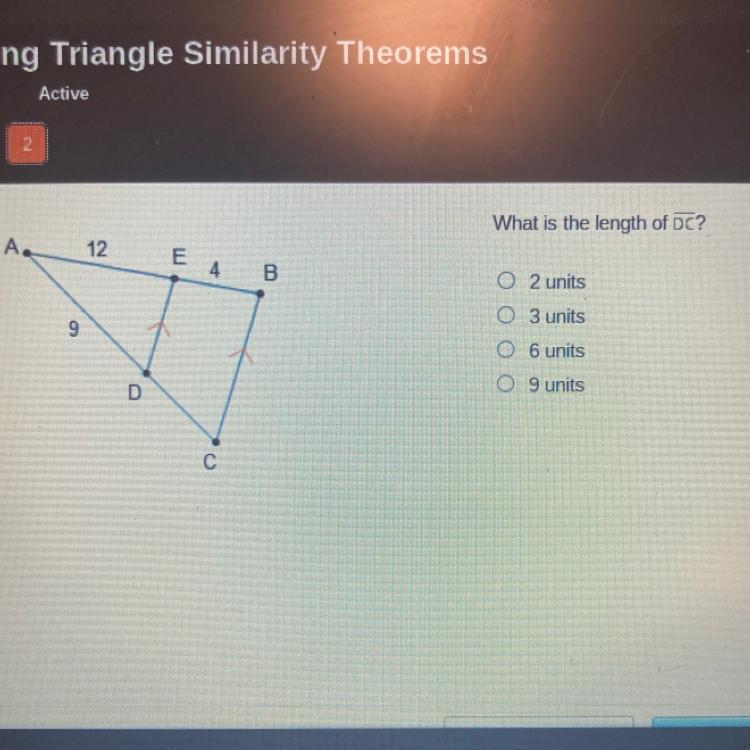
Answers
Answer:
C ) 6 units
Step-by-step explanation:
I' just guessing but based off of the other one is 4 then this must be at least 4.
Consider a continuous-time Markov chain with three states 1, 2, 3, 4, 5 and transition rates q12=1, q13 = 2, q21 = 0, q23 = 3, q31 = 0, q32 = 0. (1) Write the system of ODEs for the corresponding transition probabilities Pᵢⱼ (t) . (2) Suppose that the initial state is 1. What is the probability that after the first transition, the process X(t) enters state 2?
Answers
the probability of transitioning from state 1 to state 2 after the first transition is:
P(X(t) enters state 2 after the first transition | X(0) = 1) = 1 / 3
To write the system of ordinary differential equations (ODEs) for the transition probabilities Pᵢⱼ(t) of the given continuous-time Markov chain, we need to consider the rate at which the system transitions between different states.
Let Pᵢⱼ(t) represent the probability that the Markov chain is in state j at time t, given that it started in state i at time 0.
The ODEs for the transition probabilities can be written as follows:
dP₁₂(t)/dt = q₁₂ * P₁(t) - q₂₁ * P₂(t)
dP₁₃(t)/dt = q₁₃ * P₁(t) - q₃₁ * P₃(t)
dP₂₁(t)/dt = q₂₁ * P₂(t) - q₁₂ * P₁(t)
dP₂₃(t)/dt = q₂₃ * P₂(t) - q₃₂ * P₃(t)
dP₃₁(t)/dt = q₃₁ * P₃(t) - q₁₃ * P₁(t)
dP₃₂(t)/dt = q₃₂ * P₃(t) - q₂₃ * P₂(t)
where P₁(t), P₂(t), and P₃(t) represent the probabilities of being in states 1, 2, and 3 at time t, respectively.
Now, let's consider the second part of the question: Suppose that the initial state is 1. We want to find the probability that after the first transition, the process X(t) enters state 2.
To calculate this probability, we need to find the transition rate from state 1 to state 2 (q₁₂) and normalize it by the total rate of leaving state 1.
The total rate of leaving state 1 can be calculated as the sum of the rates to transition from state 1 to other states:
total_rate = q₁₂ + q₁₃
Therefore, the probability of transitioning from state 1 to state 2 after the first transition can be calculated as:
P(X(t) enters state 2 after the first transition | X(0) = 1) = q₁₂ / total_rate
In this case, the transition rate q₁₂ is 1, and the total rate q₁₂ + q₁₃ is 1 + 2 = 3.
Therefore, the probability of transitioning from state 1 to state 2 after the first transition is:
P(X(t) enters state 2 after the first transition | X(0) = 1) = 1 / 3
Learn more about probability here
https://brainly.com/question/32117953
#SPJ4
In a right triangle, the acute angles have the relationship sin (2x+4)=cos(46).
What is the value of x?
1.)20
2.)21
3.)24
4.)25
Answers
The required value of the acute angle x in a right angle triangle is 20. Option A is correct.
Given that
In a right triangle, the acute angles have a relationship,
sin (2x+4) = cos(46)
To determine the value of x
What are trigonometric equations?These are the equation that contains trigonometric operators such as sin, cos.. etc.. In algebraic operation.
sin (2x+4) = cos(46) - - - - - -(1)
Since,
cos(46) = cos (90 - 44)
cos(46) = sin (44)
put it in equation 1
sin (2x+4) = sin (44)
2x + 4 = 44
2x = 44 - 4
2x = 40
x = 20
Thus, the required value of the acute angle x in a right angle triangle is 20. Option A is correct.
Learn more about trigonometry equations here:
brainly.com/question/22624805
#SPJ1
Kate wants to install an in ground pool in five years. she estimates the cost will be $50,000. how
much should she deposit monthly into an account that pays 1.6% interest compounded
monthly in order to have enough money to pay for the pool in 5 years? round your answer to
the nearest dollar.
Answers
Answer:
Step-by-step explanation:
Kate should deposit $46,158.28 monthly into an account
In this question, we have been given the amount A = $50,000,
interest rate R = 1.6%
period t = 5 years
We need to find the principal amount (P)
First, convert R as a percent to decimal
r = 1.6/100
r = 0.016
Using the formula of compound interest for P,
P = A / (1 + r/n)nt
P = 50,000.00 / (1 + 0.016/12)(12)(5)
P = $46,158.28
Therefore, Kate should deposit $46,158.28
a(n) variable is characterized by infinitely uncountable values and can take any value within interval.
Answers
The correct answer is a countable variable is characterized by infinitely uncountable values and can take any value within interval.
A random variable is with an unknown value or a function that gives values to each of the results of an experiment.
Random variables are frequently identified by letters and fall into one of two categories: continuous variables, which can take on any value within a continuous range, or discrete variables, which have specified values.
Continuous random variables have an endless number of possible values and can represent any value that falls within a given range or interval.
An experiment that measures the amount of rain that falls in a city over the course of a year or the average height of a random group of 25 people are two examples of continuous random variables.
To know more about the 'countable variable' related questions
visit- https://brainly.com/question/28397043
#SPJ4
Assume that a sample is used to estimate a population mean μ . Find the 99% confidence interval for a sample of size 891 with a mean of 20.8 and a standard deviation of 17.6. Enter your answer as a tri-linear inequality accurate to 3 decimal places.19.281Incorrect < μ < 22.319

Answers
Solution:
The confidence interval is expressed as
where
\(\begin{gathered} \bar{x}\text{ or }\mu\Rightarrow sample\text{ mean} \\ z\Rightarrow confidence\text{ level value} \\ s\Rightarrow sample\text{ standard deviation} \\ n\Rightarrow sample\text{ size} \end{gathered}\)Given a 99% confidence interval for a sample size of 891 with a mean of 20.8 and a standard deviation of 17.6, this implies that
\(\begin{gathered} \bar{x}=20.8 \\ s=17.6 \\ n=891 \\ z=2.576 \end{gathered}\)By substituting these values into the above equation, we have
\(\begin{gathered} CI=20.8\pm(2.576\times\frac{17.6}{\sqrt{891}}) \\ =20.8\pm1.518866748 \\ Thus,\text{ } \\ \Rightarrow lower\text{ bound:} \\ 20.8-1.518866748=19.28113325 \\ \Rightarrow upper\text{ bound:} \\ 20.8+1.518866748=22.31886675 \end{gathered}\)Hence, we have
\(19.281<\mu<22.319\)
Determined three ways have a total cost of six dollars each apple cost $1.50 each banana cost $.30 and there’s two more bananas then apples.
Answers
The cost of the apples is 2.9 dollars.
The cost of the bananas is 5.7 dollars.
How to find the number of fruits bought?The total cost is 6 dollars, each apple cost $1.50 each banana cost $.30 and there’s two more bananas then apples.
Therefore,
let
x = number of apples
y = 2x
where
y = number of bananasTherefore, using equations,
1.5(x) + y(0.30) = 6
Hence,
where
y = 2x
1.5(x) + 2x(0.30) = 6
1.5x + 0.6x = 6
2.1x = 6
divide both sides by 2.1
x = 6 / 2.1
x = 2.9 dollars
y = 2(2.9) = 5.7 dollars
learn more on cost here: https://brainly.com/question/31245217
#SPJ1
Subtract: (7x2 + 2x – 3) – (4x2 – 3x + 1)
Answers
Answer: 3x2+5x−4
The 2 behind 3x is an exponent
Answer:
3x2 + 5x – 4
Step-by-step explanation:
Help me with this one problem please :(
Find the following arc measures.

Answers
Answer:
Arc KL \(=23\)
Arc OM \(=113\)
Step-by-step explanation:
We know that Angle NPM is equal to 90 degrees.
Therefore, Angle KPM is also equal to 90 degrees.
We are told that Arc LM is equal to 67.
Thus, the measure for Arc KL is equal to \(90-67=23\)
We also know that Angle OPN is equal to Angle KPL.
Therefore, the measure of Arc ON\(=23\)
Using that information, we know that Arc OM is equal to \(90+23=113\)
Hope I helped!
Use the Change of Base Formula and common logs or natural logs to approximate the value of logg V using a calculator. If the answer is not an integer, enter it as a decimal rounded to the nearest hundredth, if needed.
Answers
To approximate the value of log base g of V using a calculator, we can utilize the Change of Base Formula and either common logs (log base 10) or natural logs (log base e). Let's go through the steps:
1. Determine the base g and the value V for the logarithm.
2. Choose the base for the logarithm in the calculator. Let's say we want to use common logs (log base 10) for this example.
3. Apply the Change of Base Formula, which states that log base g of V is equal to log base a of V divided by log base a of g. Here, a represents the chosen base for the calculator logarithm (log base 10 in this case).
4. Enter the value V into the calculator and take the logarithm using the chosen base (log base 10).
5. Divide the result obtained in step 4 by log base a of g. In this case, divide it by log base 10 of g.
6. Round the final answer to the nearest hundredth, if necessary.
Remember to substitute the appropriate values for g and V in the formula, and choose the correct base for the logarithm in your calculator. This will provide you with an approximate value for log base g of V.
know more about logarithm
https://brainly.com/question/30226560
#SPJ11
pls help asap!!! Find the value of z

Answers
cómo se resuelve:
10-10×10+10 =?
Answers
Answer:
the answer is 10
Step-by-step explanation:
plz mark brainliest
Answer:
-80
Step-by-step explanation:
Pemdas method.
What is the solution: 4(2x + 1) = –28
Answers
Answer:
4(2x+1)=-28
2x+1=-7
2x=-7-1
2x=-8
x=-4
2x+4=3x-2 solve for x
Answers
Answer:
x = 6
Step-by-step explanation:
2x + 4 = 3x - 2
2x - 3x = -2 - 4
-x = -6
x = 6
Answer:
x = 6
Step-by-step explanation:
We are given this equation:
2x + 4 = 3x - 2
And we want to evaluate the equation for x.
To do this, we need to isolate the variable (x) on one side of the equation.
We can start by putting the numbers on one side.
We can subtract 4 from both sides of the equation to start. Remember that when solving equations, whatever we do on one side of the equation, we need to do it on the other side as well.
2x + 4 = 3x - 2
-4 -4
___________________
2x = 3x - 6
Now, let's put the variables on the other side.
Subtract 3x from both sides.
2x = 3x - 6
-3x -3x
______________
-x = -6
Now, the numbers and variables are on different sides, however we are not done yet, as we need to take care of the negatives, as x shouldn't be negative in this case.
-x is the same as -1x, or -1 * x.
So, in order to get rid of the negatives, we can either multiply or divide both sides by -1.
Let's multiply both sides by -1.
-1(-x) = -1(-6)
x = 6
The value of x is 6.
What is the domain to this graph

Answers
Answer:
x > 0
Step-by-step explanation:
The domain of the graph are all the possible values of x. Since the graph never touches the negative part of the graph, x will always be greater than 0. Thus, x > 0 meaning x will be greater (not equal to) 0.
What is the measurement of AB?
I will give brainiest to whoever answers it right.

Answers
The measurement of AB is given as follows:
AB = 16.23.
What are the trigonometric ratios?The three trigonometric ratios are defined as follows:
Sine of angle = length of opposite side divided by the length of the hypotenuse.Cosine of angle = length of adjacent side divided by the length of the hypotenuse.Tangent of angle = length of opposite side divided by the length of the adjacent side.For the angle of 52º, we have that:
AB is the hypotenuse.10 is the length of the adjacent side.Hence the measurement of AB is obtained as follows:
cos(52º) = 10/AB
AB = 10/cos(52º)
AB = 10/0.616
AB = 16.23.
More can be learned about trigonometric ratios at brainly.com/question/24349828
#SPJ1