When demonstrating that limx→3​(10x+4)=34 with ε=0.3, which of the following δ-values suffice?

Step-by-step explanation:

I know A is one because positives and negitives are oppisite but i dont know if there are more

The length of the third side is 4.

Given information:

A right-angled triangle is provided in the diagram.

So, as per the diagram,

The hypotenuse leg = √(97)

Opposite leg = 9

Let the length of the adjacent leg, which is the third side be x. By the Pythagorean theorem, we have:

x² + 9² = √(97)²

Simplifying the right side, we get:

x² + 81 = 97

Subtracting 81 from both sides, we get:

x² = 16

Apply square root property, we get,

x = +/- 4

Since the length of a side of a triangle must be positive, the length of the third side is 4.

To learn more about the Pythagoras theorem;

https://brainly.com/question/343682

#SPJ1

Answer:

3/10

Step-by-step explanation:

Half of 3/5 is 3/10

Brainliest plss

Answer:

3/10

Step-by-step explanation:

You multiply 3/5 by 1/2.

3/5 x 1/2= 3/10

Hope I could help :)

Answer:

Sally is currently 4 years old.

Step-by-step explanation:

Kaden is 18 years older than Sally now. In 5 years, Kaden will be 3 times as old as Sally. How old is Sally now?

Let Kaden's current age be \(k\) and Sally's current age be \(s\). We can write the following algebraic equation using the fact that Kaden is currently 18 years older than Sally:

\(k=s+18\)

Next, we will use the fact that in 5 years, Kaden will be 3 times as old as Sally. If Kaden and Sally's current ages are \(k\) and \(s\) respectively, then their ages in 5 years will be \(k+5\) and \(s+5\) respectively. Therefore, we have:

\(k+5=3(s+5)\)

We have two equations with two variables. To solve for either variable, we need to create an equation with only one variable. Therefore, let's substitute the first equation into the second:

\((s+18)+5=3(s+5)\)

Distribute and combine like terms:

\(s+18+5=3s+15,\\s+23=3s+15\)

Subtract \(s\) from both sides, then subtract 15 from both sides:

\(8=2s\)

Divide both sides by 2:

\(s=\frac{8}{2}=\boxed{4}\)

Therefore, Sally is currently 4 years old.

Answer:

Sally is 4 years old now.

Step-by-step explanation:

Let Sally's age = x

Kaden's age = x + 18

In 5 years, they are both 5 years older than now.

Sally will be x + 5

Kaden will be x + 18 + 5 = x + 23

"In 5 years, Kaden will be 3 times as old as Sally."

x + 23 = 3(x + 5)

x + 23 = 3x + 15

-2x = -8

x = 4

Answer: Sally is 4 years old now.

Answer:

The diameter of the floor is 6 yards

Step-by-step explanation:

Here, we are to calculate the diameter of a circular floor that has a circumference of 18.84 yards

Mathematically,

C = π * D

where C is the circumference

Plugging the values of the circumference , we have ;

18.84 = 22/7 * D

7 * 18.84 = 22D

D = (7* 18.84)/22 = 5.99 which is approximately 6 yards

The ratios of their perimeters and the ratios of their areas are 1) 3:1 and 9:1 and 2) 7:4 and 49:16.

Given the scale factor of two similar polygons, we need to find the ratio of their perimeters and the ratios of their areas,

To find the ratio of the perimeters of two similar polygons, we can simply write the scale factor as it is because the ratio of the perimeter is equal to the ration of the corresponding lengths.

1) So, perimeter = 3:1

The ratio of areas between two similar polygons is equal to the square of the scale factor.

Since the scale factor is 3:1, the ratio of their areas is:

(Ratio of areas) = (Scale factor)² = 9/1 = 9:1

Similarly,

2) Perimeter = 7:4

Area = 49/16

Hence the ratios of their perimeters and the ratios of their areas are 1) 3:1 and 9:1 and 2) 7:4 and 49:16.

Learn more about scale factors click;

https://brainly.com/question/29464385

#SPJ1

There are 194,480 ways to choose a committee of 7 from 9 girls and 8 boys. We can use combinations to solve this :

To calculate the number of ways a committee of 7 can be chosen from 9 girls and 8 boys, we can use the combination formula:

Combination formula = C(n, r) = n! / (r! * (n-r)!)

Where n is the total number of people (in this case, 9 girls and 8 boys), and r is the number of people we want to choose (in this case, 7).

Substituting the values, we get:

C(9+8, 7) = (9+8)! / (7! * (9+8-7)!)

C(17, 7) = 194,480

Therefore, there are 194,480 ways to choose a committee of 7 from 9 girls and 8 boys.

This calculation is based on the idea of combinations, which are a way of counting the number of ways to choose r items from a set of n items without regard to order. In this case, we want to choose 7 people from a group of 17 people, so we use the combination formula to calculate the number of possible combinations. The formula ensures that we count each combination only once, and that the order of selection does not matter.

To know more about combinations click here

brainly.com/question/18820941

#SPJ11

Answer:

thx sa points

Step-by-step explanation:

The probability that all five balls drawn from the urn are green, with replacement, we are not given the exact numbers of green and pink balls in the urn, we cannot determine the exact probability.

Since each draw is made with replacement, the probability of drawing a green ball on each individual draw remains constant throughout the process. Let's assume that the urn contains a total of N balls, with a certain number of them being green (denoted by G) and the remaining ones being pink (denoted by P). The probability of drawing a green ball on any given draw is then G/N.

In this case, we are drawing five balls, and we want all of them to be green. So, we multiply the probabilities of drawing a green ball on each draw together:

Probability = (G/N) * (G/N) * (G/N) * (G/N) * (G/N) = (G/N)^5

Since we are not given the exact numbers of green and pink balls in the urn, we cannot determine the exact probability. However, we can still express the probability in terms of G and N. The answer should be rounded to three decimal places.

Learn more about probability here:

https://brainly.com/question/31828911

#SPJ11

The domain of the rational function  \(\frac{x^3 + 5x^2 + 3x - 9}{x^2 -x - 2}\) is:

D: {x ∈ R| x ≠ -1, 2}

The domain will be the set of all real numbers, minus these ones that make the denominator equal to zero.

The denominator will be zero when:

x² - x - 2  =0

Using the quadratic formula we will get:

\(x = \frac{1 \pm \sqrt{(-1)^2 - 4*1*-2} }{2*1} \\\\x = \frac{1 \pm 3}{2}\)

The two solutions are:

x = (1 + 3)/2 = 2

x = (1 - 3)/2 = -1

If the numerator is not zero on these values, then we need to remove them from the domain.

When x = 2 the numerator is:

2³ + 5*2² + 3*2 - 9 = 25

When x = -1

(-1)³  + 5*(-1)²  + 3*-1 - 9 = -8

Neither of these is zero, so we need to remove x = -1 and x = 2 from the domain, then the domain is:

D: {x ∈ R| x ≠ -1, 2}

Learn more about rational functions:

https://brainly.com/question/1851758

#SPJ1

Hello !

Answer:

\(\Large \boxed{\begin{cases}x=7 \\y=6\end{cases}}\)

Step-by-step explanation:

We want to find the values of x and y that satisfy the following system of equations :

\(\begin{cases}\sf 3x-3y=3 \\\sf x+y=13\end{cases}\)

First, let's divide both sides of the first equation by 3 :

\(\begin{cases}\sf\frac{1}{3}(3x-3y)=\frac{3}{3} \\\sf x+y=13\end{cases}\)

\(\begin{cases}\sf x-y=1 \ \ \ \ (*)\\\sf x+y=13\end{cases}\)

Now let's add the two equations and combine like terms :

\(\sf x-y+(x+y)=1+13\\2x=14\)

Let's divide both sides by 2 :

\(\sf\frac{2x}{2} =\frac{14}{2} \\\boxed{\sf x=7}\)

The value of x is now known .

Let's substitute 7 for x in the first equation :

\(\sf 7-y=1\)

Substract 7 from both sides :

\(\sf 7-y-7=1-7\\-y=-6\)

Finally, let's multiply both sides by -1 :

\(\sf-1(-y)=-1(-6)\\\boxed{\sf y=6}\)

Have a nice day ;)

Answer:

-0.5f - 4.52 = -25.52 + 1f

-1.5f = 21

f = 14

Answer:

14

Step-by-step explanation:

-4.52 + 25.52 = f + 0.5f

21 = 1.5f

f = 14

If out of the 10 coin flips , 7 flips come up heads and 3 come up on tails then the probability  that the selected coin is a biased coin is   .

In the question ,

it is given that ,

let F be event in which first coin is selected

let S be event in which second coin is selected ,

So , P(F) = P(S) = 0.5 .

Let H represent the event that 7 flips out of 10 are Head ;

given that the 1st coin is fair , the probability of getting 7 heads is

P(H/F) = ¹⁰C₇(0.5)⁷(1-0.5)¹⁰⁻⁷ = 0.1172 ;

and the 2nd coin is biased and probability of getting Head = 0.85 ,

the probability of getting 7 heads is :

P(H/S) = ¹⁰C₇(0.85)⁷(1-0.85)¹⁰⁻⁷ = 0.1299

So , the total probability of getting & head and 3 tail is :

P(H) = P(H/S)P(S) + P(H/F)P(F)

= 0.1299×0.5 + 0.1172×0.5

= 0.12355 .

according to Baye's Theorem , the probability that Sally selects a biased coin is :

P(S/H) = [ P(H/S)P(S) ]/P(H)

= 0.1299×0.5/0.12355 ;

= 0.5257

Therefore , the required probability is 0.5257  .

Learn more about Probability here

https://brainly.com/question/13604343

#SPJ4

Answer: 720

Step-by-step explanation:

Volume = l x w x h, so 9 x 10 = 90, 90 x 8 = 720.

Hope this helps.

A cutoff of 10% for statistical significance is more lenient compared to the standard 5% cutoff.

What is statistical significance?

Statistical significance is a measure used in hypothesis testing to determine whether an observed result is likely to be due to chance or represents a true effect. It indicates the level of confidence that can be placed in the findings of a study or experiment

Compared to the standard 5% cutoff for statistical significance, a cutoff of 10% would be more lenient or less strict.

In statistical hypothesis testing, the significance level, often denoted as alpha (α), represents the threshold below which the p-value must fall to reject the null hypothesis. The commonly used standard cutoff is 5% (or 0.05), which means that if the p-value is less than 0.05, the result is considered statistically significant, and the null hypothesis is rejected.

When the cutoff is increased to 10% (or 0.10), it means that the threshold for statistical significance is relaxed. In other words, a p-value less than 0.10 would now be considered statistically significant, leading to a higher likelihood of rejecting the null hypothesis. This increased cutoff allows for a wider range of p-values to be considered statistically significant, making it easier to detect effects or relationships.

However, it's important to note that a higher cutoff also increases the chances of a Type I error (rejecting the null hypothesis when it is true). This means there is a higher probability of falsely concluding that there is a significant effect or relationship when it may not actually exist.

Choosing the appropriate significance level depends on the specific context, research field, and the consequences of Type I and Type II errors. Lower significance levels, like 5%, are often used to maintain a more stringent standard and reduce the risk of false positives. However, in certain cases, a higher cutoff like 10% may be suitable, such as in exploratory analyses or when the consequences of Type II errors (failing to detect a true effect) are more severe.

To know more about statistical significance visit:

https://brainly.com/question/30389845

#SPJ4

Complete Question:

Compared to the standard 5% cutoff for statistical significance, a cutoff of 10% would be more lenient or less strict?

The interquartile range of the data set is equal to 6.

The interquartile range is a measure of statistical dispersion, or data spread. The IQR is also known as the midspread, middle 50%, or middle 50%.

The interquartile range is a measurement of a data set's "middle fifty." A range is a measurement of where a set's beginning and end are located.

Given data set is 2 4 6 8 10 12. The upper range is 8 10 12 and the lower range is 2 4 6.

Calculate the median of the upper range and the lower range and subtract it.

Median upper range = 10

Median lower range = 4

The interquartile range is calculated as,

IQR = 10 - 4 = 6

To know more about the interquartile range follow

https://brainly.com/question/4102829

#SPJ1

The solar array panel has dimensions of 240 feet by 40 feet, resulting in a total area of 9,600 square feet.

To find the area of the top face of one solar array panel, we can use the formula for the area of a rectangle:

Area = Length * Width

Given that the length of the solar array panel is 240 feet and the width is 40 feet, we can substitute these values into the formula:

Area = 240 feet * 40 feet

Multiplying the numbers:

Area = 9,600 square feet

Therefore, the area of the top face of one solar array panel is 9,600 square feet. This represents the total surface area of the panel when viewed from the top. The area calculation is straightforward by multiplying the length and width of the rectangle.

For more such questions on dimensions

https://brainly.com/question/28107004

#SPJ8

Answer:

19 nickels, 57 dimes, and 114 quarters

Step-by-step explanation:

57/3 = 19

1 × 19 = 19

3 × 19 = 57

6 × 19 = 114

The Alexander family used their sprinkler for 35 hours, and the Chen family used their sprinkler for 30 hours.

To find out how long each sprinkler was used, we can set up a system of equations. Let's say the Alexander family used their sprinkler for x hours, and the Chen family used their sprinkler for y hours.

From the given information, we know that the water output rate for the Alexander family's sprinkler is 30 liters per hour. Therefore, the total water output from their sprinkler is 30x liters.

Similarly, the water output rate for the Chen family's sprinkler is 40 liters per hour, resulting in a total water output of 40y liters.

Since the combined total water output from both sprinklers is 2250 liters, we can set up the equation 30x + 40y = 2250.

We also know that the families used their sprinklers for a combined total of 65 hours, so we can set up the equation x + y = 65.

Now we can solve this system of equations to find the values of x and y, which represent the number of hours each sprinkler was used.

By solving the equation we get,

The Alexander family used their sprinkler for 35 hours, and the Chen family used their sprinkler for 30 hours.

To know more about sprinkler  refer here:

https://brainly.com/question/30777999

#SPJ11

Answer:

20 containers

Step-by-step explanation:

Given:

D = 0.07N

Where,

D = Amount of deposits

N = Number of containers

If D = $1.40 find N

D = 0.07N

1.40 = 0.07N

Divide both sides by 0.07

N = 1.40 / 0.07

= 20

N = 20 containers

if you deposit $1.40, you will buy a total of 20 containers.

The solution is, at 500 miles, will the rental fee be the same under both plans A and B.

An equation is a  mathematical statement that is made up of two expressions connected by an equal sign.  In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal. For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an 'equal' sign.

here, we have,

from the given information, we get,

Plan A:   y = .2x + 75

Plan B:   y = .35x

Find an xy pair that satisfies both (intersection)

Substitute Plan B's y for Plan A

.35x = .2x + 75

.35x - .2x = 75

.15x = 75

x = 500

Hence, The solution is, at 500 miles, will the rental fee be the same under both plans A and B.

To learn more on equation click:

brainly.com/question/24169758

#SPJ2

Answer:

16.25

Step-by-step explanation:

Answer:x>-15

Step-by-step explanation:

5-2x<35

You would need to subtract both sides by 5

5-5 cancel each other out

35-5=30

Then divide 30 by -2 and you get -15

Answer:116

Step-by-step explanation:

By definition, a rhombus will have equal opposite angles.

Also by definition, the two angles on the same side of a rhombus are supplementary, or add up to 180 degrees.

Using this, we can make the equation 2c-12+c=180, 3c-12=180, 3c=192, and c =64

Now that we have found out c is 64, we plug it into the angle 2c-12 to get

2*64-12=116.

So again by definition, angle J will be 116 degrees since its an opposite angle.

Answer:

The answer is R is neither reflexive, nor symmetric, nor

transitive.

Step-by-step explanation:

Let A = {1, 2, 3, 4, 5, 6}.

A relation R is defined on set A as:

R = {(a, b): b = a + 1}

R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}

We can find (a, a) ∉ R, where a ∈ A.

For instance,

(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) ∉ R

R is not reflexive.

It can be observed that (1, 2) ∈ R, but (2, 1) ∉ R.

R is not symmetric.

Now, (1, 2), (2, 3) ∈ R

But, (1, 3) ∉ R

R is not transitive

Thus, R is neither reflexive, nor symmetric, nor transitive.

There are 5 full square and 6 triangles that are half squares.

      5 + (6)(1/2) = 5 + 3 = 8

You could also break this into smaller shapes (like a big triangle on the top and a smaller triangle and rectangle on the bottom and use area formulas to calculate the area.  But counting works well in this example.

Answer: 8

Step-by-step explanation:

First you split up this shape into two different shapes, a triangle and trapezoid

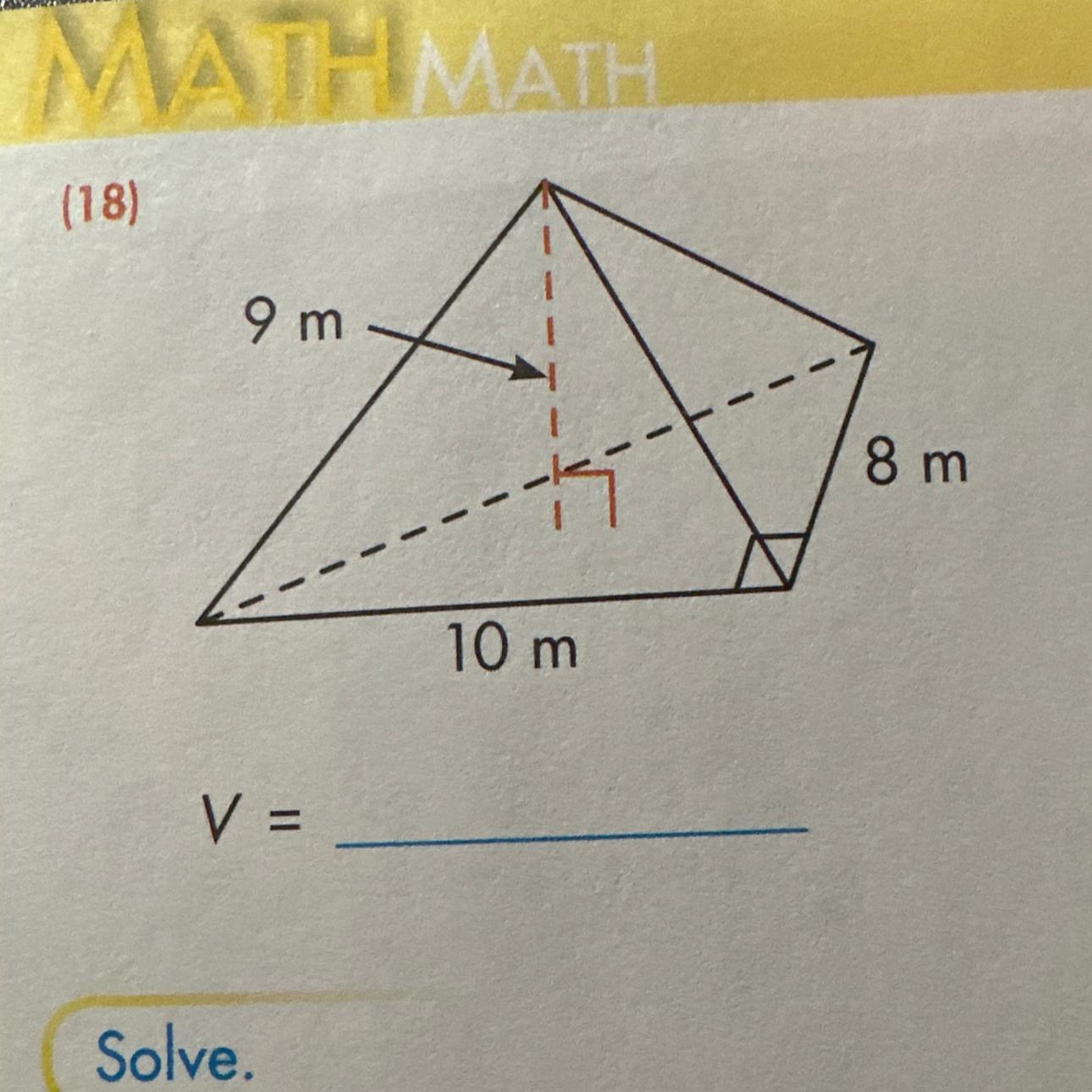
Put a line through the coordinates (-2,2) to  (-1,2); the top is a triangle and the other is a trapezoid

Area of the trapezoid is A = .5x (base1 + base2) x height

base1 of the trapezoid goes from -4 to -1 which is 3

base2 goes from -2 to -1 which is 1

height is 0 to 2 whcich is 2

A = .5 x (3+1) x 2 = 4

Now area of a triangle is A = .5 x base x height

the base goes from -2 to 2 which is 4

the height goes from 2 to 4 which is 2

A = .5 x (4) x (2) = 4

Area of the Trapezoid + Area of the Triangle = Total Area

4 + 4 = 8

Answer:

-528/25

Step-by-step explanation:

Answer:

-----------------------

Using the formula for the union of two sets:

where

We are given that:

Plugging in the values, we get:

Therefore, set B contains 42 elements.

Answer:

A

Step-by-step explanation:

reflections don't change size or shape just like mirrors

Answer:

To determine the value of W, we need to find the value of x that satisfies the given condition.

If (x-4) is a factor of X^2 - X - W = 0, it means that when we substitute x = 4 into the equation, it should equal zero.

Let's substitute x = 4 into the equation:

(4)^2 - (4) - W = 0

16 - 4 - W = 0

12 - W = 0

To solve for W, we isolate the variable:

W = 12

Therefore, the value of W is 12.