Answers
Answer:
the answer is 12, I hope this helps
Step-by-step explanation:
its 12 because the original Pentagon is 2 times the smaller ones height, therefore you multiply 6 times 2 and get 12
Step-by-step explanation:
C. 12cm
sana makatulong
Related Questions
factor-\(x^2+10x+21=0\)
Answers
Answer:
x = 5 ± √46
Step-by-step explanation:
\(-x^2 + 10x + 21 = 0\)
Take -1 common from L.H.S.
\(=> -1(x^2 -10x - 21) = 0\)
Take -1 to R.H.S.
\(=> x^2 - 10x - 21 = 0\)
Solve x using quadratic formula.
\(=> x = \frac{-(-10) + \sqrt{10^2 - 4 \times (-21) \times 1} }{2 \times 1} \: or \:\frac{-(-10) - \sqrt{10^2 - 4 \times (-21) \times 1} }{2 \times 1}\)
\(=> x = \frac{10 + \sqrt{100 + 84} }{2} \: or \:\frac{10 - \sqrt{100 + 84} }{2}\)
\(=> x = \frac{10 + \sqrt{184} }{2} \: or \: \frac{10-\sqrt{184} }{2}\)
\(=> x = \frac{10 + 2\sqrt{46} }{2} \: or \: \frac{10 - 2\sqrt{46} }{2}\)
\(=> x = (5 + \sqrt{46} ) \: or \: (5 - \sqrt{46} )\)
Solve the system of equations below using the substitution method. y = 3x − 1y = - 4x 6
Answers
Answer:
x = 1; y = 2
Step-by-step explanation:
y = 3x − 1
y = -4x + 6
In the first equation, y = 3x - 1.
Substitute 3x - 1 for y in the second equation.
3x - 1 = -4x + 6
7x = 7
x = 1
Substitute 1 for x in the first original equation.
y = 3x - 1
y = 3(1) - 1
y = 3 - 1
y = 2
Solution: x = 1; y = 2
Which is the correct piece wise definition for the function:

Answers
Answer:
Step-by-step explanation:
Start with the piecewise definition of the absolute value function
y = f(x) = |x|
\(f(x) = \left \{ {f(x);\;{x\ge=0} \atop {{-f(x);\;{x < 0}} \right.\)
Substitute x + 5 for f(x)
\(|x+5| = \left \{ {x+5;\;{x+5\ge=0} \atop {{-(x+5);\;{x + 5 < 0}} \right.\)
Note that at x = 5, |x + 5| = 0 and therefore we have a unique point (-5, -2). This is where the function changes
Simplify the inequalities
x + 5 ≥ 0 ==> f(x) = x ≥ -5
-(x+5) < 0 ==> -x -5 < 0 = -x < 5 or x >=5
Separate the two pieces
y = (x + 5); x ≥ -5
y = -x - 5; x < -5
Subtract 2 from both sides of the function
y = (x + 5) - 2 when x ≥ -5 or y = x + 3 when x ≥ -5
y = -x - 5 - 2 when x < -5 or y = - x - 7 when x < -5
Correct answer choice is the last one
y = x + 3 for x ≥ -5 and y = -x -7 for x < -5
If you look at the attached graph of y = |x| -2 you will see this is consistent with the above piecewise function
For example at x = -3 which is greater than x = -5, y = 0 and x+3 = -3 + 3 = 0
At x = -7 which is less than -5, also y = 0 and -x -7 = -(-7) - 7 = 7-7 = 0

Find the height of a cylinder with a volume of 600.8 cm and a radius of 42
cm.
Answers
Answer:
9.21 cm
Step-by-step explanation:
Solve for x.
1)
6
2)
3
3)
4
4)
5

Answers
The value of x for the chord AC intersecting another chord ED is equal to 4 which makes the option 3). 4 correct.
Chords intersecting in the interior of a circleWhen two chords are intersecting each other inside a circle, then the product of the segments of one of the chord is equal to the product of the segments of the other chord.
The chords AC and ED are interesting each other, so;
9(4x) = 8(4x + 2)
36x = 32x + 16
36x - 32x = 16 {collect like terms}
4x = 16
x = 16/4 {divide through by 4}
x = 4
Therefore, the value of x for the chord AC intersecting another chord ED is equal to 4
Know more about chord here:https://brainly.com/question/15298662
#SPJ1
pls help if you can asap!!!!

Answers
Answer: x= 6
Step-by-step explanation:
Since the shape is a parallelogram, the angles will either be equal to each other or add up to 180.
You can see they do not look the same so they add up to equal 180
12x + 3 +105 = 180
12x + 108 = 180
12x = 72
x = 6
5 (t+3)=-3.5 solve for t
Answers
Answer:
t=-3.7
Step-by-step explanation:
5 (t+3)=-3.5
solving the bracket we have;
5t+15=-3.5
collect like terms
5t=-3.5-15
5t=-18.5
divide both sides by 5;
t=-3.7
The value of t in the given algebraic expression is; t = -2.3
We are given the equation;
5(t + 3) = 3.5
Using distributive property on the left hand side, we have;
5t + (5 × 3) = 3.5
5t + 15 = 3.5
Using subtractive property of equality, subtract 15 from both sides to get;
5t + 15 - 15 = 3.5 - 15
5t = -11.5
Divide both sides by 5 to get;
5t/5 = -11.5/5
t = -2.3
Read more at; https://brainly.com/question/23202310
Kayden went shopping for a new pair of sneakers. Sales tax where he lives is 9.25%. The price of the pair of sneakers is $36. Find the total price including tax. Round to the nearest cent.
Answers
Answer:
$39.33, including sales tax.
Step-by-step explanation:
9.25% of 36 = 3.33
36 + 3.33 = 39.33
$39.33
Answer:
39.30$(Remember to add the dollar sign and 0 in the decimals place, just write it as I did)
Step-by-step explanation:
36*0.0925=3.33
3.33 is tax
rounded to nearest tenth is 3.3
36+3.3=39.3
make it into money form
39.30$
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
use the washer method to find the volume of the solid generated when the region r bounded by y=3x, y=x, and y=9 is revolved about the y-axis.
Answers
The volume of the solid generated by revolving the region bounded by the curves y = 3x, y = x, and y = 9 about the y-axis can be found using the washer method.
First, let's find the points of intersection between the curves. Setting y = 3x and y = x equal to each other, we get:
3x = x
2x = 0
x = 0
So, the curves intersect at the point (0, 0).
Next, we'll find the limits of integration. The region r is bounded between y = x and y = 9. The lower limit of integration is x = 0, and the upper limit of integration is x = 3.
Now, let's consider a vertical slice of the region at a given x-value. The radius of the outer circle (larger radius) is y = 9, and the radius of the inner circle (smaller radius) is given by the equation of the line y = x. The thickness of the washer is dx.
The volume of each washer can be calculated using the formula V = π(R^2 - r^2)dx, where R is the radius of the outer circle and r is the radius of the inner circle.
For the given problem, the volume can be calculated as follows:
V = ∫[0,3] π((9)^2 - (x)^2)dx
Evaluating this integral, we get:
V = π∫[0,3] (81 - x^2)dx
= π[(81x - (x^3)/3)]|[0,3]
= π[(81(3) - (3^3)/3) - (81(0) - (0^3)/3)]
= π[243 - 9]
= 234π
Therefore, the volume of the solid generated is 234π cubic units.
Learn more about calculus and volume calculations using the washer method here:
https://brainly.com/question/30637777
#SPJ11
The following are an example of what type of angles? * 120° 60° O/ Vertical Angles Linear Pair/Complimentary Angles /Supplementary Angles
Answers
we know that
Supplementary angles sum 180 degrees
so in this problem
120 and 60and 60
suppose researchers marked 800 turtles and later were able to trap a total of 300 individuals in that population, of which 200 were marked. what is the estimate for total population size?
Answers
Using Marked recapature formula for estimation on population size we get,
the estimate for total population size is 1200.
Marked recaputure Method :
first step is to capture and mark a sample of individuals. The assumption behind mark-recapture methods is that the proportion of marked individuals recaptured in the second sample represents the proportion of marked individuals in the population as a whole. In algebraic terms,
R/S = M/N
where R --> second time marked
S---> size of sample second time
N --> estimate population size
M ---> Marked in start point
We have given that ,
Total marked turtles by researchers (M) = 800
Second time total sample size (S) = 300
second time marked turtles(R) = 200
we have to find out estimate for total population size .
For this , Mark -Recapture method is very efficient to calculate estimate for total population size.
putting all known values in above formula we get, R/S = N/M
=> 200/300 = 800/N
=> 800× 300 = N× 200
=> N × 200 = 240000
=> N = 240000/200
=> N = 1200
so, the estimate for total population size is 1200.
To learn more about Marked recapature method , refer:
https://brainly.com/question/18828154
#SPJ4
Solve the inequality -9y > 9
Answers
Hello!
-9y > 9 <=>
<=> -9y ÷ (-9) > 9 ÷ (-9) <=>
<=> y < -1 <=>
<=> y ∈ { -∞; -1 }
Good luck! :)
What types of values of the test statistic for the kruskal wallace test support the alternative hypothesis?.
Answers
One of the non-parametric tests used it as a generalized version of such Mann Whitney U test is the Kruskal-Wallis test.
Explain the term Kruskal-Wallis Test?One of the non-parametric tests used as an expanded version of a Mann Whitney U test is the Kruskal-Wallis test.
It's employed to test the null hypothesis, which claims that "k" samples were taken from the same population or an identical population and that the median for each sample was the same or same. The null hypothesis can be expressed mathematically as S1 = S2=..... = Sk if Sj is the population median again for jth group and sample with in Kruskal-Wallis test. Naturally, the alternative theory would be that Si and Sj are not equal. This indicates that there are different pairs in at least 1 pair of groups and samples.As a result, it has been used to investigate the null hypothesis, which claims that 'k' samples were taken from populations that were either identical or similar and had medians that were similar or slightly similar.
To know more about the Kruskal-Wallis Test, here
https://brainly.com/question/29106748
#SPJ4
The population of mosquitoes in a certain area as a function of inches of rainfall is modeled in the table. The function is quadratic.
Rainfall (in.) Population (millions)
0 0
1 9
2 16
3 21
4 24
5 25
6 24
Enter your answers in the boxes.
The x-intercept represents that after in. of rain there are mosquitoes.
Answers
The x-intercept represents that after 10 in. of rain, there are mosquitoes in that area.
How to Interpret Quadratic Equations?The function is quadratic. The standard form of the quadratic equation is;
f(x) = ax² + bx + c
Here (a, b, c) are the real numbers and (x) is the variable. For the first point (0,0). The equation becomes,
f(0) = a(0)² + b(0) + c
c = 0
For the second point (1,9). The equation becomes,
f(1) = a(1)² + b(1) + 0
9 = a + b ----(1)
For the third point (3, 21). The equation becomes,
f(3) = a(3)² + b(3) + 0
21 = 9a + 3b ----(2)
Solving eq 1 and eq 2 simultaneously gives;
a = -1 and b = 10
Thus, our quadratic equation is;
f(x) = -x² + 10x
At f(x) = 0, x = 10.
Thus, x-intercept is at x = 10
Read more about Quadratic Equations at;https://brainly.com/question/1214333
#SPJ1
What's the distance between points (2,-3) and (5,1)
Answers
Answer:
\(d = 5\)
General Formulas and Concepts:
Order of Operations: BPEMDAS
Distance Formula: \(d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Step-by-step explanation:
Step 1: Define points
(2, -3)
(5, 1)
Step 2: Solve for d
Substitute: \(d = \sqrt{(5-2)^2+(1-(-3))^2}\)Subtract: \(d = \sqrt{(3)^2+(1-(-3))^2}\)Change signs: \(d = \sqrt{(3)^2+(1+3)^2}\)Add: \(d = \sqrt{(3)^2+(4)^2}\)Exponents: \(d = \sqrt{9+16}\)Add: \(d = \sqrt{25}\)Evaluate: \(d = 5\)PLSSSSSS HELP
-14 = -(-2x+2)
Answers
\(-14=-(-2x+2) \\ \\ 14=-2x+2 \\ \\ 12=-2x \\ \\ \boxed{x=-6}\)
Answer: x=-6
Step-by-step explanation:
Kalyan Singhal Corp. makes three products, and it has three machines available as resources as given in the following LP problem: Maximize contribution = 3X₁ +5X₂ +7X3 1X₁ +7X₂ + 4X3 ≤ 100 2X1 + 1X₂ + 7X3 ≤ 110 8X₁ + 4X₂ + 1X3 ≤ 100 X₁, X2, X3 20 (C₁: hours on machine 1) (C₂: hours on machine 2) (C3: hours on machine 3) a) Using a computer software for solving LP, the optimal solution achieved is: (round your response to two decimal places). X₁² = X₂ = (round your response to two decimal places). = X3² (round your response to two decimal places). Contribution (objective value) = (round your response to two decimal places). b) Machine 1 has Machine 2 has Machine 3 has hours of unused time available at the optimal solution (round your response to two decimal places). hours of unused time available at the optimal solution (round your response to two decimal places). hours of unused time available at the optimal solution (round your response to two decimal places). dollars to the firm (round your response to two decimal places). c) An additional hour of time available for third machine, is worth d) An additional 5 hours of time available for the second machine, at no cost to the firm, are going to increase the objective value by dollars (round your response to two decimal places).
Answers
a) Contribution (objective value) = $132.14
b) The firm earns $132.14 at the optimal solution.
c) An additional hour of time available for the third machine is worth $0.14 to the firm.
d) An additional 5 hours of time available for the second machine will increase the objective value by $3.69.
The best result obtained from using computer software to solve the LP problem is: X1 = 11.43, X2 = 12.86, X3 = 5.71
b) The number of unused hours at the ideal solution is:
Machine 1 still has 8.57 hours of time left.
There are no hours left on Machine 2 at the moment.
There are still 94.29 hours left on Machine 3.
c) The shadow price of the third limitation is worth an extra hour of time available for the third machine. With the exception of increasing the right-hand side of the third constraint by one unit, we can solve the LP problem using the same constraints to determine the shadow price. Using LP to solve this issue, we discover that the shadow price for the third constraint is
For such more questions on optimal solution
https://brainly.com/question/31025731
#SPJ8
Can anyone help me on question 5?

Answers
B) from -infinity to -3
C) -3 to 2
D) -infinity to -3 and 2 to infinity
E) -infinity to infinity
F) no because the slope is linnear in 2 stops but has a different slope in both spots meaning it can’t be a linnear function or an exponential funtion
1/5 divided by -1/14?
Answers
Answer:
-2.8 or -14/5
Step-by-step explanation:
To divide one fraction by another, there is a really cool method called Keep Change Flip
Keep the first fraction
Change the division sign to multiplication
Flip the numbers on the last fraction
Let's try it out.
Keep the 1/5
Change the ÷ to a ×
Flip the -1/14 to a -14/1
1/5 × -14/1
Multiply the top numbers by each other first
1 × -14 = -14
Now the bottom numbers
5 × -1 = -5
The fraction we have now is -14/5
It can also be written as -2.8
The approximate weights of two animals are 5.12 x 102 lbs. and 6.8 x 102 lbs. Find the total weight of the two animals. Write the final answer in scientific notation with the correct number of significant digits.
Answers
The total weights of the two animals is 11. 92 × 10² Ibs
How to determine the valueIn order to determine the total weights, we take the following steps:
Determine the weight of the animalsAdd the weight of the animalsThe weight of the animals are given as;
5.12 x 102 lbs 6.8 x 102 lbsNow, let's add the weights:
= 5. 12 × 10² + 6. 8 × 10²
Add the values
= 11. 92
It is important to note that the powers are similar and should be written as one
We then have the sum to be;
= 11. 92 × 10² Ibs
Thus, the total weights of the two animals is 11. 92 × 10² Ibs
Learn more about index notation here:
https://brainly.com/question/10339517
#SPJ1
Answer: the Correct answer is 1.2 x 10^3
Step-by-step explanation: You add 5.12 and 6.8 and get 11.92 x 10^2
you then need to round up to 12 and move the decimal up for scientific notation 1.2 x 10^3
The correct answer is 1.2 x 10^3
please give Branliest
the mean of this distribution is 0.009 and the sd is 0.004. would you expect about 95% of the samples to have their variances within 0.008 of 0.009? why or why not?
Answers
No, we would not expect about 95% of the samples to have their variances within 0.008 of 0.009.
The variance of a normal distribution with mean μ and variance σ^2 is given by σ^2, which in this case is equal to (0.004)^2 = 0.000016.
The variance of the sample means, on the other hand, is given by σ^2/n, where n is the sample size. In order for about 95% of the samples to have variances within 0.008 of 0.009, we would need the sample size to be approximately equal to:
n ≈ σ^2 / (0.008 - 0.009)^2 = 62500
This means that we would need very large samples for this to be true. However, if the sample size is relatively small, then the distribution of sample means will not necessarily be normal and the Central Limit Theorem may not apply.
In that case, the distribution of sample variances will not necessarily follow the same pattern as the distribution of the population variance, and it may not be possible to make predictions about the sample variances based on the population parameters.
To learn more about mean click on,
https://brainly.com/question/30598523
#SPJ4
explain how 984/616=123/77
Answers
And you get
984/616
Hope this helps!
Brainliest is much appreciated!
Answer:
984/616 is equal to 123/77 because it is simplified, also meaning reduced by finding the GCF (greatest common factor), which in this case is 8. So therefore, when you divide the numerator of 984 by 8, you get 123, and when you divide the denominator of 616 by 8 as well, you will get 77.
Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros. Write the function in standard form. -2, 3, 6
Answers
Answer:
To write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros -2, 3, 6, we can use the Linear Factorization Theorem1.
The theorem states that if a polynomial function f has zeros x = r1, x = r2, …, x = rn (where r1, r2, …, rn are distinct real numbers), then f(x) can be factored as follows:
f(x) = a(x - r1)(x - r2)…(x - rn)
where a is a nonzero constant.
So for this problem, we have:
f(x) = (x - (-2))(x - 3)(x - 6)
Multiplying this out gives:
f(x) = (x + 2)(x - 3)(x - 6)
Expanding this expression gives:
f(x) = x^3 - 7x^2 + 12x + 36
Therefore, the polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros -2, 3, 6 is:
f(x) = x^3 - 7x^2 + 12x + 36
I hope this helps! Let me know if you have any other questions.
Step-by-step explanation:
Solve M = 2pt^4 - 7px for x
Answers
Answer:
p= m over 2t to the 4th power -7x
Step-by-step explanation:
yb better
help finding the volume
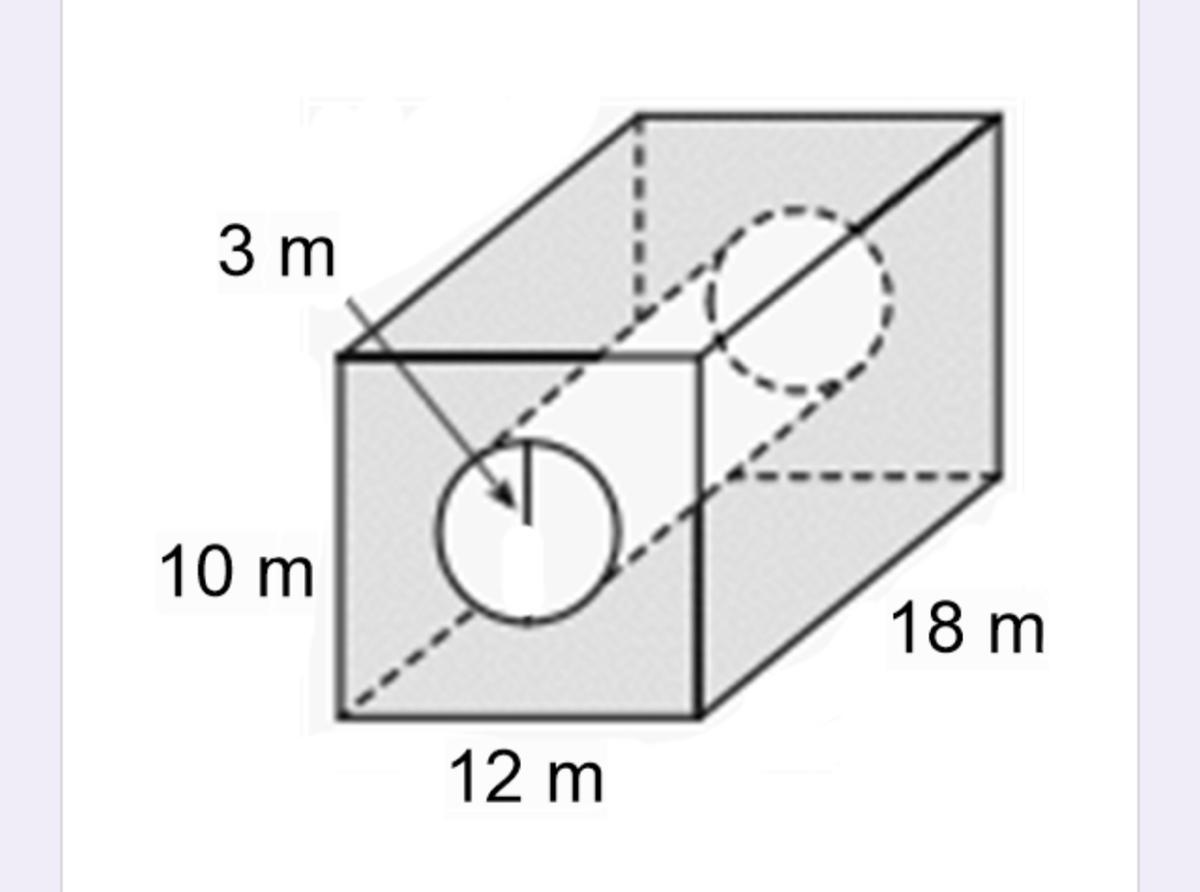
Answers
Answer:
1651.06 m³
Step-by-step explanation:
the volume of the whole block is base area times height :
Vb = 10 × 12 × 18
but we have to deduct the volume of the removed central cylinder.
the volume of the cylinder is again base area times height :
Vc = pi×r² × 18 = pi×3² × 18 = pi×9×18
so, the volume of the object is
V = Vb - Vc = 2160 - 508.94 = 1651.06 m³
5. On a test that has a normal distribution, a score of 48 falls three standard deviations
above the mean, and a score of 24 falls one standard deviation below the mean.
Determine the mean of this test.
Answers
Answer:
The mean of this test is 36.'
RATE 5 STARS NALANG PARE MARK BRAINLIEST NADEN
You polled 2805 Americans and asked them if they drink tea daily. 724 said yes. With a 95% confidence level, construct a confidence interval of the proportion of Americans who drink tea daily. Specify the margin of error and the confidence interval in your answer.
Answers
According to the information, the 95% confidence interval for the proportion of Americans who drink tea daily is approximately (0.2485, 0.2766). The margin of error is approximately 0.0140.
How to construct a confidence interval?To construct a confidence interval for the proportion of Americans who drink tea daily, we can use the formula:
Confidence Interval = p ± Z * \(\sqrt\)((p * (1 - p)) / n)Where,
p = the sample proportion
Z = the critical value corresponding to the desired confidence level
n = the sample size
Given:
Sample size (n) = 2805Number of Americans who drink tea daily (p) = 724/2805 ≈ 0.2580 (rounded to four decimal places)Z-value for a 95% confidence level ≈ 1.96Now, let's calculate the confidence interval and margin of error:
Confidence Interval = 0.2580 ± 1.96 * \(\sqrt\)((0.2580 * (1 - 0.2580)) / 2805)Confidence Interval ≈ (0.2485, 0.2766)Margin of Error = 1.96 * \(\sqrt\)((0.2580 * (1 - 0.2580)) / 2805)Margin of Error ≈ 0.0140According to the information, the 95% confidence interval for the proportion of Americans who drink tea daily is approximately (0.2485, 0.2766), with a margin of error of approximately 0.0140.
Learn more about confidence interval in: https://brainly.com/question/32278466
#SPJ4
find the area enclosed by the curve x = t2 − 3t, y = t and the y-axis.
Answers
The area under the curve is \(\frac{6 \sqrt{3}}{5}\).
Consider the following parametric equations:\($$x=t^2-3 t \text { and } y=\sqrt{t} \text { and the } y \text {-axis. }$$\)
The objective is to find area enclosed by the curve using the formula.
The area under the curve is given by parametric equations x=f(t), y=g(t), and is traversed once as t increases from α to β, then the formula for calculating the area under the curve:
\($$A=\int_\alpha^\beta g(t) f^{\prime}(t) d t$$\)
The curve has intersects with y-axis. so x=0
\($$\begin{aligned}t^2-3 t & =0 \\t(t-3) & =0 \\t & =0 \text { or } t=3\end{aligned}$$\)
Now we have to draw the graph,
Let f(t)=\(t^2-3 t, g(t)=\sqrt{t}$\)
Differentiate the curve f(t) with respect to t.
\(f^{\prime}(t)=2 t-3\)
Now, find the area under the curve use the above formula.
\(\begin{aligned}A & =\int_0^3(\sqrt{t})(2 t-3) d t \\& =\int_0^3(2 t \sqrt{t}-3 \sqrt{t}) d t \\& =\int_0^3\left(2 t^{\frac{3}{2}}-3 t^{\frac{1}{2}}\right) d t \\& =\left[2 \frac{t^{\frac{5}{2}}}{\frac{5}{2}}-3 \frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right]_0^3 \\& \left.\left.=\left[\frac{4 t^{\frac{5}{2}}}{5}-2 t^{\frac{3}{2}}\right]_0^3\right]^{\frac{5}{2}}\right] \\\\\end{aligned}$$\)
\(& =\left[\frac{4(3)^{\frac{5}{2}}}{5}-2(3)^{\frac{3}{2}}\right]-\left[\frac{4(0)^{\frac{5}{2}}}{5}-2(0)^{\frac{3}{2}}\right]\)
\($\begin{aligned}& =\left[\frac{4(3)^{\frac{5}{2}}}{5}-2(3)^{\frac{3}{2}}\right]-\left[\frac{4(0)^{\frac{5}{2}}}{5}-2(0)^{\frac{3}{2}}\right] \\& =\frac{4(3)^{\frac{5}{2}}}{5}-2(3)^{\frac{3}{2}}-0 \\& =\frac{6 \sqrt{3}}{5}\end{aligned}\)
Therefore, the area of the curve is \(\frac{6 \sqrt{3}}{5}\).
For more question such on parametric equations
https://brainly.com/question/28537985
#SPJ4

patti and her family were going on a vacation to Florida they drove 8 ½ hours on sunday and 7 ½ hours on Monday, if the entire trip was going to take them 19 ½ hours, how much longer, do they need to drive

Answers
Answer:
3½ thats the answer your welcome
