Answers
Answer:
y=-1/2x-3
Step-by-step explanation:
The line goes down 1 and over 2, and has a y-intercept of -3.
Related Questions
PhotoMath couldn’t help me!

Answers
Answer:
option B is correct answer of this question
hope it helps
Answer:
Option B
Step-by-step explanation:
As,
In all the options 3rd process of the simplification Only B option is correct as,
When the bases are same the exponents get added
So, Option B is only the correct simplification of
\({ ({9}^{ \frac{1}{2} })}^{2} \)
To - 9
Rick had $20. He spent $10 on food, $6 on a movie ticket, and saved the rest.
( Pls answer both questions )
A. How much money did he save ?
B. What fraction of the total amount did he save ?
Answers
he saved 1/5
Answer:
He saved $4
1/5 of the total amount saved
Step-by-step explanation:
20 - 16 = 4
If f (p) = 7p³ - 5p² + 1/3p what is f(3)

Answers
Answer: f(3) = 145 ==> 1st option
Step-by-step explanation:
f(p) = 7p³ - 5p² + 1/3p
f(p) = 7p³ - 5p² + p/3
f(3) = 7(3)³ - 5(3)² + (3)/3
f(3) = 7(27) - 5(9) + 1
f(3) = 189 - 45 + 1
f(3) = 144 + 1
f(3) = 145 ==> 1st option
What is the length of the hypotenuse of the triangle? Triangle A B C. Side A C is 8 centimeters and side C B is 15 centimeters. Hypotenuse A B is unknown. StartFraction 94 EndFraction cm StartFraction 161 EndFraction cm 17 cm 23 cm AWNSER ASPA!

Answers
Answer:
The hypotenuse is 17
Step-by-step explanation:
We can use the Pythagorean theorem since this is a right triangle
a^2 + b^2 = c^2 where a and b are the legs and c is the hypotenuse
8^2 + 15^2 = c^2
64 + 225 = c^2
289 = c^2
Take the square root of each side
sqrt(289) = sqrt(c^2)
17 = c
Answer:
17 cm
Step-by-step explanation:
Since this is a right triangle, we can use the Pythagorean Theorem.
\(a^2+b^2=c^2\)
where a and b are the legs and c is the hypotenuse.
In this triangle, 8 cm and 15 cm are the legs, because they form the right angle. The hypotenuse is unknown.
a= 8
b= 15
\(8^2 + 15^2= c^2\)
Solve the exponents on the left side of the equation.
8^2= 8*8= 64
\(64+15^2=c^2\)
15^2= 15*15= 225
\(64+225=c^2\)
Add 64 and 225
\(289=c^2\)
c is being squared. We want to get c by itself, so we must perform the inverse. The inverse would be taking the square root.
Take the square root of both sides.
\(\sqrt{289} =\sqrt{c^2}\)
\(\sqrt{289} =c\)
\(17=c\)
c= 17 cm
The length of the hypotenuse is 17 centimeters.
Please anyone that can help me

Answers
Answer:
\(|\frac{x}{y} |\)
Step-by-step explanation:
Pre-SolvingWe are given the following expression: \(\sqrt\frac{x^3y^5}{xy^7}\), where x > 0 and y > 0.
We want to simplify it.
To do that, we can first simplify what is under the radical, then take the square root of what is left.
Recall that when simplifying exponents, we don't want any negative or non-integer radicals left.
SolvingTo simplify what is under the radical, we can remember the rule where \(\frac{a^n}{a^m} = a^{n-m}\).
So, that means that \(\frac{x^3}{x} = x^2\) and \(\frac{y^5}{y^7} = y^{-2}\) .
Under the radical, we now have:
\(\sqrt{x^2y^{-2}}\)
Now, we take the square root of both exponents to get:
\(|xy^{-1}|\)
The reason why we need the absolute value signs is because we know that x > 0 and y > 0, but when we take the square root of of \(x^2\) and \(y^{-2}\) , the values of x and y can be either positive or negative, so by taking the absolute value, we ensure that the value is positive.
However, we aren't done yet; remember that we don't want any radicals to be negative, and the integer of y is negative.
Recall that if \(a^{-n}\), that is equal to \(\frac{1}{a^n}\).
So, by using that,
\(|x * \frac{1}{y} |\)
This can be simplified to:
\(|\frac{x}{y} |\)
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
Find the point on the y-axis that is 7 units from the point (−7, −5).
Answers
The point which is on the y-axis and is the y axis and is 7 units from the point (-7, -5) is;
What is the point on the y-axis that is 7 units from the point (−7, −5)?Since the point is on the y-axis, it follows that it's x-coordinate is zero and hence; the point is; (0, y).
The distance is therefore 7 units and hence;
7² = (-7-0)² + (y - (-5))²
49 -49 = (y +5)²
0 = y +5
y = -5
Read more on distance between points;
https://brainly.com/question/23848540
#SPJ1
Use the distance formula to find the distance between the points (−1,6) and (−1,7).
Answers
The required distance between the points (−1,6) and (−1,7). is 1 unit.
Given that,
using the distance formula to evaluate the distance between the points (−1,6) and (−1,7).
Distance is defined as the object traveling at a particular speed in time from one point to another.
Here,
The distance formula is given as,
D = √[[x₂ - x₁]² + [y₂+ - y₁]²]
Substitute the values in the above equation,
D = √[[-1 + 1]² + [7 - 6]²]
D = √[0 + 1]
D = 1
Thus, the required distance between the points (−1,6) and (−1,7). is 1 unit.
Learn more about distance here:
https://brainly.com/question/28956738
#SPJ1
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
Julio tiene 12 años de edad y su padre tiene 42 años. ¿Cuántos años tendrá Julio cuando su padre tenga el doble de su edad?
Answers
Julio will be 30 years old when his father is twice his age.
To determine the age at which Julio will be twice his father's age, we need to find the age difference between them and then add that difference to Julio's current age.
Currently, Julio is 12 years old, and his father is 42 years old. The age difference between them is 42 - 12 = 30 years.
For Julio to be twice his father's age, the age difference needs to remain the same as it is currently. Therefore, when Julio is x years old, his father will be x + 30 years old.
Setting up an equation to solve for x:
x + 30 = 2x
Simplifying the equation, we subtract x from both sides:
30 = x
Thus, when Julio is 30 years old, his father will be 30 + 30 = 60 years old. At this point, Julio will indeed be twice his father's age.
Therefore, Julio will be 30 years old when his father is twice his age.
Note : the translated question is Julio is 12 years old and his father is 42 years old. How old will Julio be when his father is twice his age?
For more such question on age. visit :
https://brainly.com/question/30994122
#SPJ8
Please help with thissss

Answers
Answer:
180 degrees
Step-by-step explanation:
Lets call the unknown Angle next to angle C "ANGLE D"
1. Your given the angle 45 degrees.
2. (45 degree angle) can correspond to Angle D,
because of the alternate exterior angles definition- two lines (angles) that are on diagonal opposite sides of one another outside of the two parallel lines.
3: (45 degree angle) is an alternate exterior angle to its corresponding diagonal angle Angle D, this can also be said for (Angle C) and (angle B).
4: Now that the angles are known- (Angle C) is an alternate exterior angle to (Angle B). (45 degree angle) is an alternate exterior angle to Angle D
We can now use
The alternate Exterior angles Theorem- If two parallel lines are intersected by a transversal, then the alternate exterior angles are congruent.
4: we now know that (45 degree angle) is congruent to Angle D. And (angle C) is congruent to (angle B).
-Angle D and (45 Degree angle) are both 45 degrees since they are both alternate exterior angles to one another. And (Angle C) and (Angle B) have the same angle measure because they are alternate exterior angles to one another.
5: take a look at (angle C) and Angle D notice the transversal- (line that intersects two parallel lines), and how it creates a linear pair. Notice that the transversal has created the angles of (angle B) and (45 degree angle) to be linear pairs as well.
- Linear Pair definition- If two adjacent lines have rays pointing in opposite directions they are linear pairs.
Also the definition of a Linear Pair identifies as Supplementary. Supplementary is an angle that has a total of 180 degrees.
6: If (45 degree angle) and Angle B make a linear pair, and linear pairs have a total of 180 degrees, then solve for the angle measure of (angle B)
180= 45 + measure of (angle B)
180-45= 135
135 = measure of (angle B)
45 + 135= 180 degrees
7: The measure of (Angle B) is 135 degrees and since (Angle B) is congruent to (Angle C), the measure of (Angle C) is 135 degrees.
Therefore, (45 degree angle) and (Angle B) are 180 degrees total and (Angle C) and (Angle D) are 180 degrees total.
Now, that all exterior angle measures are found, it can be concluded that Angle A) is the same as the total measure of its exterior angle, since it is the same line that makes up the linear pair.
Therefore, (Angle a) is 180 degrees.
there are 7 people to be seated in a row. answer the following.A. Find The Number Of Combinations If There Are No Restrictions On The Seating Arrangements. B. There Are Three Friends That Must Sit Together. Find The Number Of Combinations In Which The Three Friends Are Next To Each Other. C. Suppose That An Usher Randomly Assigns The Seats To The 7
Answers
A) The Number of Combinations if there are no restrictions on the seating arrangements are 5040 ways.
B) There are three friends That must sit together
in 36 ways.
C) Three friends are next To each other in 144 different ways.
Total number of people = 7 and seated in a row.
Combination is arrangement of objects in a particular order. The formula of combination is
ⁿCₓ = n!/(n-x)! x!
n --> total number of objects
we have to determine how many ways can 7 be seated in a row.
A) if there are no restrictions on seating arrangement, The number of possible ways = n!
Here, n! = 7!
= 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040 ways.
Therefore, there are 5040 ways that the people can be seated when there is no restriction on the seating arrangement.
b) There are three friends that must sit Together. The three persons can be arranged in 3!
The possible number of ways = 3! × 3! × 1
= 3× 2×1 ×3×2×1
= 36
C) If there are three friends must sit next to one another. There are total seven persons . Three persons sit next to one another. The possible number of ways = 3! × 4!
= ( 3 × 2 × 1) × (4 × 3 × 2 × 1)
= 6 × 24
= 144 ways
Therefore, if there are 3 sit next to one another, there are 144 ways of seating arrangement.
To learn more about Combination, refer:
https://brainly.com/question/28065038
#SPJ4
please help 3/4 divided by 1/8
Answers
Answer:
6
Step-by-step explanation:
please help 3/4 divided by 1/8
3/4 : 1/8 =
3/4 x 8 =
24/4 =
6
Which ordered pair is a solution of the equation shown? A.-3/4,- 1/2 B. 0,3/4 C.4/3, 1/2 D. 4, 3/2
pls hurry = 50 point
Answers
Answer:
the answer is b, c, d, a, respectively
Help with number 5 show work and explanation
ASAP PLEASE!!!!!!

Answers

What is the surface area of the composite figure shown?

Answers
Answer:
531 m²
Step-by-step explanation:
9x9x5=405 (5 sides that are 9x9, including the bottom)
1/2x9x7x4=126 (4 triangles on top)
405+126=531
sharmila recived 81 texts in 9 minutes
Answers
Answer:
Step-by-step explanation:
81 texts in 9 hours
So you do 81 divided by 9
Which givrs you 9 text an hour
Leo invested $1900 in an account with annually compounded interest. After 3 years, he had $2275 in the account. What was the interest rate of the account? Round your answer to one decimal place. Do not write the percent sign.
Answers
Answer:
6.2%
Step-by-step explanation:
got the wrong answer and this was the right one omm
Solve the equation of N+5/-16=-1
Answers
Step-by-step explanation:
N + 5 = -1
-16
N = - 1 + 5
16
N = -16 + 5
16
N = -11
16
N = -0.6875 = -0.7
questions 1 and 2, please

Answers
Answer:
too blurry cant read it
Step-by-step explanation:
.........................................................
Graph each equation using the intercepts. Re-write in standard form first if necessary 2x-y=-42x=-4X=-2(2,0)O-y- -4Y=4(0,4)

Answers
EXPLANATION:
Given;
We are given the linear equation below;
\(2x-y=-4\)Required;
We are required to graph the equation of the line using the intercepts.
Step-by-step solution;
The graph of a line in standard form is given as;
\(Ax+By=C\)Note that the equation given already satisfies this condition. We can re-arrange the equation in the slope-intercept form which is;
\(y=mx+b\)We now have the following;
\(\begin{gathered} 2x-y=-4 \\ Subtract\text{ }2x\text{ }from\text{ }both\text{ }sides: \\ -y=-4-2x \\ Multiply\text{ }all\text{ }through\text{ }by\text{ }-1: \\ \\ y=4+2x \\ OR \\ y=2x+4 \end{gathered}\)We can plot for at least 2 points by using the intercepts, that is when x = 0 and when y = 0;
\(\begin{gathered} When\text{ }x=0: \\ y=2(0)+4 \\ \\ y=4 \end{gathered}\)Also,
\(\begin{gathered} When\text{ }y=0: \\ 0=2x+4 \\ Subtract\text{ }2x\text{ }from\text{ }both\text{ }sides: \\ -2x=4 \\ Divide\text{ }both\text{ }sides\text{ }by\text{ }-2: \\ x=-2 \end{gathered}\)We now have the points;
\((0,4)\text{ }and\text{ }(-2,0)\)We can now plot these on a graph paper, and then extend the line at both ends. That is at the point where you have (-2, 0), we can draw the line continuously to the left and from the point where you have (0, 4), you can also draw the line continuously to the right.
With the aid of a graphing tool, the graph will come out like the one shown below;
ANSWER:
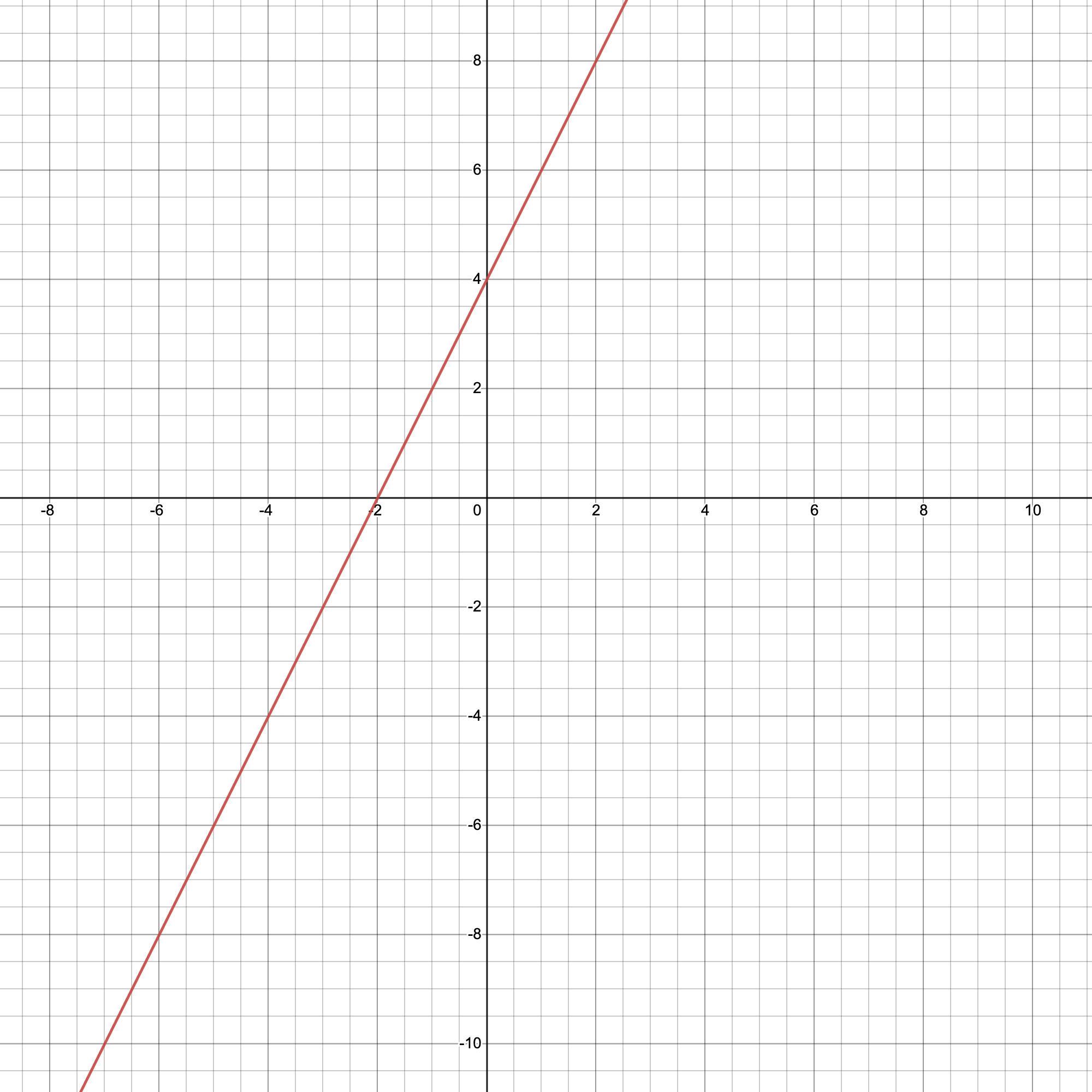
Jamil always throws loose change into a pencil holder on his desk and takes it out every two weeks. This time it is all nickels and dimes. There are 2 times as many dimes as nickels, and the value of the dimes is $1.05 more than the value of the nickels. How many nickels and dimes does Jamil have?
Answers
Answer:
7 nickels and 14 dimes
Step-by-step explanation:
In tricky word problems like this you have to translate the word problem to algebraic equations
Let number of nickels = N
Let number of dimes = D
2 times as many nickels as dimes is saying that
the nmber of dimes = twice the number of nickels
and translates to D = 2N (1)
Value of D dimes = 10D cents since each dime is 10 cents
Value of N nickels = 5N cents since each nickel is 5 cents
$1.05 = 105 cents
So,
Value of dimes is $1.05 more than value of nickels translates to :
10D - 5N = 105 (2)
Since we have D = 2N we can use this relation to substitute for the value of D in terms of N
10D - 5N ==> 10(2N) - 5N = 20N - 5N = 15N
From (2) we get
15N = 105
N = 105/15 = 7
So there are 7 nickels
D = 2N = 2 x 7 = 14
So there are 14 dimes
Hence there are 7 nickels and 14 dimes
Let's check and see if our answer is right by plugging this value into the second equation
10D - 5N = 10 x 14 - 5 x 7 = 140 - 35 = 105 cents =$1.05
What is the area of this rectangle? Rectangle with width 5.1 cm and height 11.2 cm. Responses 16.3 cm2 16.3 cm, 2 32.6 cm2 32.6 cm, 2 57.12 cm2 57.12 cm, 2 571.2 cm2

Answers
The area of a rectangle with a width of 5.1 cm and a height of 11.2 cm is 57.12 cm².
To find the area of a rectangle, we multiply its length by its width. In this case, the width is given as 5.1 cm and the height (or length) is given as 11.2 cm.
Area = length × width
Area = 11.2 cm × 5.1 cm
Calculating the product, we get:
Area = 57.12 cm²
Therefore, the area of the rectangle is 57.12 cm².
The correct answer is: 57.12 cm².
It is important to note that when calculating the area of a rectangle, we should always include the appropriate unit of measurement (in this case, cm²) to indicate that we are dealing with a two-dimensional measurement. The area represents the amount of space covered by the rectangle's surface.
So, the area of a rectangle with a width of 5.1 cm and a height of 11.2 cm is 57.12 cm².
for more such question on rectangle visit
https://brainly.com/question/2607596
#SPJ8
at the given number in the indicated base
Answers
The table shows how many children and adults prefer each of two different fruits. How would you find the joint relative frequency of being an adult who prefers watermelon?%0D%0A%0D%0AWatermelon%09Grapes%09Total%0D%0AChild%09132%0985%09217%0D%0AAdult%09111%09117%09228%0D%0ATotal%09243%09202%09445%0D%0A%0D%0AA.%0D%0ADivide 111 by 228.%0D%0A%0D%0AB.%0D%0ADivide 111 by 243.%0D%0A%0D%0AC.%0D%0ADivide 111 by 445.%0D%0A%0D%0AD.%0D%0ADivide 243 by 445.
Answers
The joint relative frequency is calculated by dividing the frequency of a specific subset (in this case, the number of adults who prefer watermelon) by the total number of data points.
Here, the specific subset is adults who prefer watermelon, which is 111. The total number of data points is the sum of all children and adults, regardless of fruit preference, which is 445.
So, to find the joint relative frequency of being an adult who prefers watermelon, you would divide 111 by 445.
Hence, the correct answer is:
C. Divide 111 by 445.
The radius of a circle is 11 yards. What is the circle's area?
Use 3.14 for .
Answers
Answer:
\(\displaystyle 380,13271108...\:yd.^2\)
Step-by-step explanation:
\(\displaystyle {\pi}r^2 = A \\ \\ 11^2\pi = A \hookrightarrow 121\pi = A \\ \\ \boxed{380,13271108... = A}\)
If you want to follow what the exercise wants, then multiplying \(\displaystyle 3,14\)by the square of the radius will give you \(\displaystyle 379,94\:yd.^2.\)
I am joyous to assist you at any time.
On which number line the location of point P represent the probability of an event that is likely, but not certain?

Answers
The straight line that best represents something probable but not certain is option D.
It shows a probability of approximately 80%.
Data Classification For the given datasets, circle the data classification (categorical or quantitative) and type of data (Nominal or Ordinal or Continuous or Discrete). A. Height of sunflowers in a field. 1. Categorical or Quantitative 2. Nominal or Ordinal or Continuous or Discrete B. Jersey color of all the NCAA football teams.1. Categorical or Quantitative 2. Nominal or Ordinal or Continuous or Discrete
Answers
the data classification (categorical or quantitative) and type of data (Nominal or Ordinal or Continuous or Discrete)
A. Height of sunflowers in a field.
1.Quantitative
2.Continuous
B. Jersey color of all the NCAA football teams.
1.Categorical
2.Nominal
A. Height of sunflowers in a field.
1.Quantitative
2.Continuous
B. Jersey color of all the NCAA football teams.
1.Categorical
2.Nominal
Data classification is a process of organizing data into categories based on their characteristics, attributes, or features. There are two main types of data classification:
Categorical Data: Data that can be divided into categories or classes. For example, color, gender, and type of cuisine are all examples of categorical data. Categorical data can be further classified into two types:
a. Nominal Data: Data that does not have an inherent order or ranking. For example, hair color, eye color, and favorite movie are all examples of nominal data.
b. Ordinal Data: Data that has a natural order or ranking. For example, education level (high school, college, postgraduate), star rating (1 star, 2 stars, 3 stars), and satisfaction level (very unsatisfied, unsatisfied, neutral, satisfied, very satisfied) are all examples of ordinal data.
Quantitative Data: Data that can be measured and expressed as a number. For example, height, weight, and time are all examples of quantitative data. Quantitative data can be further classified into two types:
a. Continuous Data: Data that can take on any value within a specified range. For example, height, weight, and temperature are all examples of continuous data.
b. Discrete Data: Data that can only take on specific values. For example, number of children in a family, number of pets, and number of rooms in a house are all examples of discrete data
To learn more about Discrete Data:
https://brainly.com/question/9041886
#SPJ4
Determine if ✓ 8 is rational or irrational and give a reason for
a reason for your answer.
Answers
(-11)×[-52+(-17)-(-39)]
Answers
Step-by-step explanation:
(-11)×[-52+(-17)-(-39)]-11×[-52-17+39)]-11×[-69+39]-11×[30]-330