What would be the result of executing the following code? int[] x = {0, 1, 2, 3, 4, 5}
Answers
The code provided initializes an integer array named "x" with the values 0, 1, 2, 3, 4, and 5.
In more detail, when this code is executed, the following steps take place:
1. The variable "x" is declared as an integer array.
2. The array "x" is initialized with the values 0, 1, 2, 3, 4, and 5.
3. The array "x" is assigned memory to store these values.
After executing this code, the variable "x" will be an integer array with six elements. Each element will contain a different value: the first element will be 0, the second element will be 1, the third element will be 2, and so on, up to the sixth element, which will be 5.
It is important to note that array indexing in most programming languages starts from 0. So, to access the first element of the array "x", you would use "x[0]". To access the second element, you would use "x[1]", and so on.
In summary, executing the given code will result in an integer array "x" with the values 0, 1, 2, 3, 4, and 5 stored in its elements.
Learn more about integer arrays: https://brainly.com/question/29989214
#SPJ11
Related Questions
(1 point) college officials want to estimate the percentage of students who carry a gun, knife, or other such weapon. how many randomly selected student
Answers
Probability Theory
P (K) =\(\frac{n (K) }{n (S)}\)
P(K) : probability of selected K
n (K) : number of occurence of K
n (S) : number of all occurence
In question is not contain information about the number of students who curry a gun, knife, or other weapon and the number of all students. so, we can desribe that :
n (A) : the number of occurence of students who curry a gun
n (B) : the number of occurence of students who curry a knife
n (C) : the number of occurence of students who curry other weapon
and the number of all students is n ( A U B U C) -> union of sets
how many randomly selected student? in question, there is no specific about the student. so, we can answer with :
1) probability of students who curry a gun
P (A) = \(\frac{n (A) }{n (AUBUC)}\)
2) probability of students who curry a knife
P (B) = \(\frac{n (B) }{n (AUBUC)}\)
3) probability of students who curry other weapon
P (C) = \(\frac{n (C) }{n (AUBUC)}\)
and if question want to estimate with percentage, we can multiply with 100%. example :
1) percentage of probability of students who curry a gun
P (A) = \(\frac{n (A) }{n (AUBUC)}\) x 100%
read more about probability at https://brainly.com/question/9772981
#SPJ4
7, -21, 63, ..
Find the 15th term of the geometric sequence
Answers
Geometric Sequence :
Every term in a geometric sequence is obtained by multiplying the term before it by the same number. \(A_{n}\) = \(a_{}\) \(r^{n-1}\) is the general term for it. The common ratio is denoted by the number 'r'. Any term in the sequence can be used to find it by dividing it by the term before it.
'a' is the first term of the sequence, n is the \(n^{th}\) term.
Given geometric sequence :
7 , -21 , 63 , ....
Here, first term = a = 7
common ratio = r = \(\frac{-21}{7}\) = -3
n = 15.
Then, \(15^{th}\) term = \(A_{15}\) = 7 x \((-3)^{15-1}\)
= 7 x \((-3)^{14}\) = 7 x 4,782,969
= 33,480,783 .
To know more about geometric sequence, visit,
https://brainly.com/question/13614184
#geometric sequence
Have you ever looked closely at sound waves? They may look like random lines at first glance. But if you zoom in, you will see that they are very similar to graphs of trigonometric functions. Like trigonometric functions, they appear as oscillating waves with a measurable frequency and amplitude.
In music, each note has a specific frequency, measured in hertz. The units for hertz are cycles per second (1 ÷ sec), or sec-1. The most common note used for tuning an instrument is the A next to middle C. Pianists often call this note A4. This note has a frequency of 440 Hz. This means that the note A4 has 440 cycles in one second. Any musical note can be graphed using the function f(x) = sin (y × 2πx), where y is the frequency of the note and x is the time in seconds.
Part A Using this graphing tool, graph the function for note A4. Paste a copy of the graph below, keeping the default scale. What does it look like? Why does it appear like that?
Answers
The graph of the sine function f(x) = sin(400πx) is given by the image at the end of the answer.
How to graph the sine function?The sine function in this problem is defined as follows:
f(x) = sin (y × 2πx).
In which the relevant variable for the graph is the variable y, which is the number of cycles in a single second of the wave.
In this problem, it is states that the note has a frequency of 440 Hz, meaning that it has 440 cycles in one second, thus the equation is:
f(x) = sin (440 × 2πx).
f(x) = sin (880πx).
The function is not multiplied by any value, hence the amplitude is of 1, meaning that the function oscillates between 0 and 1, and also there is not any phase shift or vertical shift, meaning that it oscillates between -1 and 1 starting at the origin.
More can be learned about the sine function at https://brainly.com/question/21902442
#SPJ1

Choose the numbers that are equivalent to 2 7/9.
Answers
The equivalent fractions here are: 14/18 , 21/27 , 28/36 , 35/45 , 42/54.
Given, the number 7/9
7/9 = (7/9 × 2/2) = 14/18
7/9 = (7/9 × 3/3) = 21/27
7/9 = (7/9 × 4/4) = 28/36
7/9 = (7/9 × 5/5) = 35/45
7/9 = (7/9 × 6/6) = 42/54
hence the equivalent fractions here are:
14/18 , 21/27 , 28/36 , 35/45 , 42/54
Equivalent fractions are those fractions that reflect the same value even if they may have distinct numerators and denominators. For instance, the fractions 9/12 and 6/8 are comparable as both, when simplified, equal 3/4.
When reduced to their most basic form, all equivalent fractions become the same fraction.
Learn more about Fractions here:
brainly.com/question/2328150
#SPJ9
X + 3 = -6+4x help please
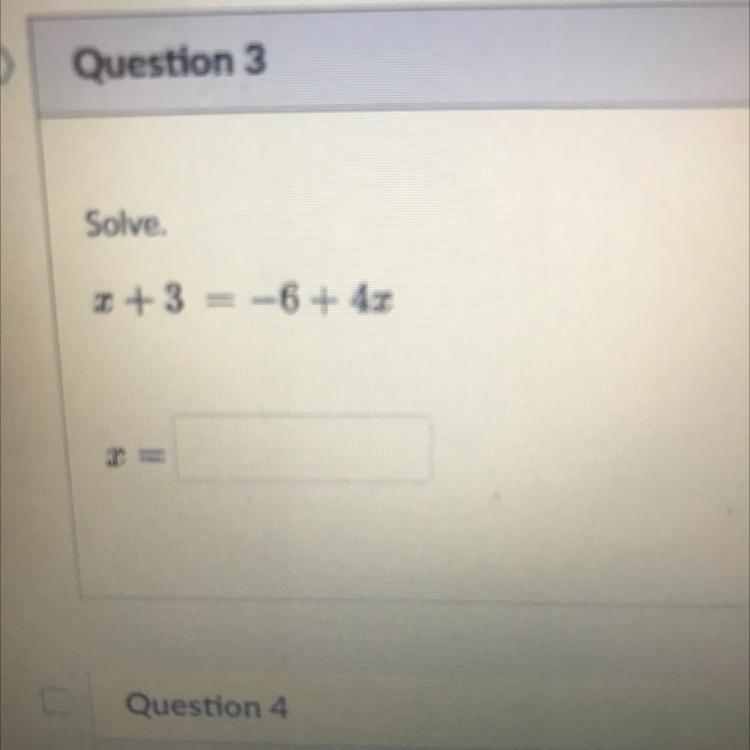
Answers
Answer:
x = 3
Step-by-step explanation:
I hope this helps!
Answer:
x = 3
Step-by-step explanation:
I hope this helps
line v has a slope of - 5/2. line w has a slope of - 2/5. are line v and line q parallell, perpendicular, or neither?
Answers
Answer:
neither
Step-by-step explanation:
Parallel lines need to have the same slope.
Perpendicular lines have opposite reciprocal slopes.
-5/2 and -2/5 are opposite reciprocals nor are they equal.
How do I solve for y in this equation? 2x+y=-9
Answers
Answer:
Step-by-step explanation:
y=-2x-9
subtract both sides by 2x
Find the value of 4x2 + 2y where y= 0.5 and x= 3
Answers
Answer:
37
Step-by-step explanation:
substitute the given values for x and y into the expression
4x² + 2y
= 4(3)² + 2(\(\frac{1}{2} \) )
= 4(9) + 1
= 36 + 1
= 37
Which of the following can be used for the line that a shape is to be reflected over?
Answers
Answer:
i don't know i need help with this one too
Step-by-step explanation:
An elementary teacher wants to know if the school has a higher proportion of left-handed students than the usual proportion of 0.10. The teacher surveys a random sample of 50 students, and finds that 7 are left-handed. 1) What is the sample proportion ? O 0.14 O 0.10 07 2) What is the hypothesized proportion po? O 0.14 O 0.5 O 0.10 3) What is the sample size n? O 50 O 7 4) What is the test statistic z? O 0.943 0 -0.815
Answers
1) The sample proportion is 0.14 (7 left-handed students out of 50 total students surveyed).
2) The hypothesized proportion po is 0.10 (the usual proportion of left-handed students).
3) The sample size n is 50 (the number of students surveyed).
4) The test statistic z is 1.32.
1) The sample proportion is calculated by dividing the number of left-handed students by the total number of students surveyed. In this case, 7 left-handed students out of 50 gives a sample proportion of 7/50 = 0.14.
2) The hypothesized proportion (p₀) is the usual proportion of left-handed students, which is given as 0.10.
3) The sample size (n) is the total number of students surveyed, which is 50.
4) The test statistic (z) can be calculated using the formula: z = (sample proportion - hypothesized proportion) / sqrt((hypothesized proportion * (1 - hypothesized proportion)) / sample size). In this case, z = (0.14 - 0.10) / sqrt((0.10 * (1 - 0.10)) / 50) = 0.04 / sqrt(0.09 / 50) ≈ 0.943.
To calculate the test statistic z, we use the formula:
z = (sample proportion - hypothesized proportion) / standard error
The standard error is calculated as:
standard error = sqrt((po * (1-po)) / n)
Plugging in the values, we get:
standard error = sqrt((0.10 * (1-0.10)) / 50) = 0.0499
Then,
z = (0.14 - 0.10) / 0.0499 = 1.32
Since the calculated z-value of 1.32 is greater than the critical value of 1.645 (using a significance level of 0.05 for a two-tailed test), we can conclude that there is not enough evidence to reject the null hypothesis that the proportion of left-handed students at the school is the same as the usual proportion of 0.10.
To learn more about hypothesized proportion, click here:
brainly.com/question/28187749
#SPJ11
Help!!! Use 1st and 2nd differences to determine if the following table of values is linear, quadratic or neither.
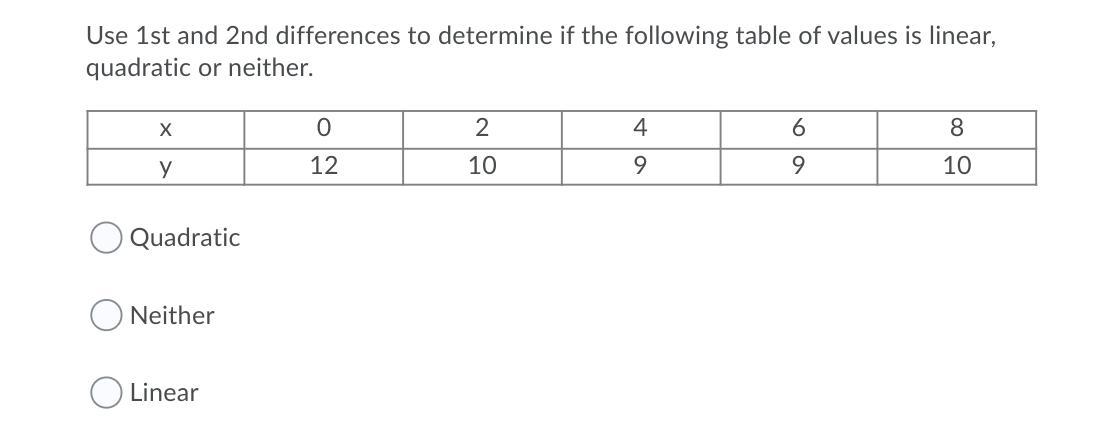
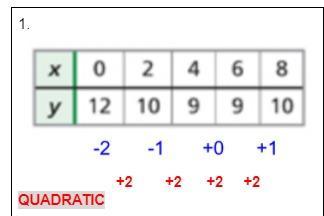
Answers
Answer:
This would be QUADRATIC
which of the following is equivalent to 2/3 divided by 5/6 ?
Answers
Answer:
.8 or 8/10 or 4/5
Step-by-step explanation:
Six points have these coordinates 1 2 4 6 5.6 5.6 4.7 4.5 3.8 3.1 2.8 Portions of the MINITAB printout are shown here The regression equation is y = 6.03-0.557 x Predictor Coef 6.0333 -0.55714 SE Coef 0.1587 0.04074 38.03 -13.68 0.001 0.003 Constant Predicted Values for New Observations New Obs 1 MINITAB Output 5.1762) 2.1206) Fit 95.0% PI SE Fit 4.9190 0.0926 1.5762 0.1961 95.0% c (4.6619, (1.0317, (4.3805, (0.8548 5.4576) 2.2975) X denotes a point that is an outlier in the predictors. Values of Predictors for New Observations New Obs 1 2.00 8.00(a) Find a 95% confidence interval for the average value of y when x = 2. (Enter your answers to four decimal places.)
(b) Find a 95% prediction interval for some value of y to be observed in the future when x = 2. (Enter your answers to four decimal places.)
Answers
A. the 95% confidence interval for the average value of y when x = 2 is (4.9241, 5.4283).
B. The 95% prediction interval for some value of y to be observed in the future when x = 2 is (4.6619, 5.4576).
(a) To find a 95% confidence interval for the average value of y when x = 2, use the provided information:
Predicted Value for New Obs 1 (x = 2): 5.1762
SE Fit: 0.0926
Now, apply the formula for confidence intervals:
CI = Predicted Value ± (t-value * SE Fit)
For a 95% confidence interval and degrees of freedom = 4 (6 points - 2 parameters), the t-value is approximately 2.776 (using a t-table).
CI = 5.1762 ± (2.776 * 0.0926)
CI = (5.1762 - (2.776 * 0.0926), 5.1762 + (2.776 * 0.0926))
CI = (4.9241, 5.4283)
So, the 95% confidence interval for the average value of y when x = 2 is (4.9241, 5.4283).
(b) To find a 95% prediction interval for some value of y to be observed in the future when x = 2, use the information provided:
95.0% PI: (4.6619, 5.4576)
The 95% prediction interval for some value of y to be observed in the future when x = 2 is (4.6619, 5.4576).
To learn more about confidence interval, refer below:
https://brainly.com/question/24131141
#SPJ11
find the coefficient of x^10 in (1 x x^2 x^3 ...)^n
Answers
The coefficient of x^10 in (1 x x^2 x^3 ...)^n is C(n, 10), or "n choose 10".
The expression (1 x x^2 x^3 ...) represents an infinite geometric series with a common ratio of x. The sum of an infinite geometric series with a common ratio of x and a first term of 1 is given by:
sum = 1 / (1 - x)
To find the coefficient of x^10 in (1 x x^2 x^3 ...)^n, we need to find the coefficient of x^10 in the expansion of (1 / (1 - x))^n. We can use the binomial theorem to expand this expression as follows:
(1 / (1 - x))^n = C(n, 0) + C(n, 1)x + C(n, 2)x^2 + ... + C(n, n)x^n
where C(n, k) is the binomial coefficient "n choose k", which gives the number of ways to choose k items from a set of n items. The coefficient of x^10 in this expansion is given by C(n, 10), since the term x^10 only appears in the (n-10)th term.
Therefore, the coefficient of x^10 is C(n, 10), or "n choose 10".
Learn more about infinite geometric series here
brainly.com/question/23602882
#SPJ4
Find the critical value Za/2 corresponding to a 99.5% confidence level.
0.0025
2.575
2.81
1.96
Answers
Answer:
The correct option is;
2.81
Step-by-step explanation:
The critical value \(Z_{\alpha /2}\), is found from the z score table as follows, where the the confidence level is 99.5
Therefore, we have α = 1 - 99.5/100 = 1 - 0.995 = 0.005
α/2 = 0.0025
The critical value is thus found from the z-score table value of 1 - 0.0025 = 0.9975
From the z-table, we can find the 0.9975 score on the row with z = 2.8 where 0.9975 can be located under the 0.1 column giving the critical value as 2.81
solve for h V=2πr^2h

Answers
Answer: h= V/2πr^2
Step-by-step explanation:
Isolate the variable by dividing each side by factors that don't contain the variable.
Chris worked 51 hours last week. His rate is $31.00 per hour. What were his gross earnings for the week?
Answers
Answer:
Step-by-step explanation:
51 x $31 an hour = $1581 is his gross earnings for the week
A team has probability 2/3 of winning whenever it plays. Find each of the following probabilities that the team will win. a). At most 4 out of 5 games. b). At most 4 out of 5 games, given that it has won already the first 3 games of a 5-game series.
Answers
The probability that the team will win at most 4 out of 5 games is 8/9.
To calculate the probability of winning at most 4 out of 5 games, we need to find the probability of winning 0, 1, 2, 3, or 4 games.
The probability of winning exactly k games out of 5 is given by the binomial distribution formula:
P(X = k) = (5 choose k) * (2/3)^k * (1/3)^(5-k)
Where "n choose k" is the binomial coefficient, representing the number of ways to choose k items from a set of n items. In this case, it represents the number of ways to win k games out of 5.
Using this formula, we can calculate the individual probabilities:
P(X = 0) = (5 choose 0) * (2/3)^0 * (1/3)^5 = (1) * (1) * (1/243) = 1/243
P(X = 1) = (5 choose 1) * (2/3)^1 * (1/3)^4 = (5) * (2/3) * (1/81) = 10/243
P(X = 2) = (5 choose 2) * (2/3)^2 * (1/3)^3 = (10) * (4/9) * (1/27) = 40/243
P(X = 3) = (5 choose 3) * (2/3)^3 * (1/3)^2 = (10) * (8/27) * (1/9) = 80/243
P(X = 4) = (5 choose 4) * (2/3)^4 * (1/3)^1 = (5) * (16/81) * (1/3) = 80/243
To find the probability of winning at most 4 out of 5 games, we sum up these probabilities:
P(X <= 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) = (1/243) + (10/243) + (40/243) + (80/243) + (80/243) = 8/9.
To know more about the binomial distribution, refer here:
https://brainly.com/question/29137961#
#SPJ11
Those activities that enable a person to describe in the detail the system that solves the need is called?
Answers
Those activities that enable a person to describe in the detail the system that solves the need is called "System design".
What is a system design?The method of defining the components of a system consists, modules, and components, the various interfaces of those components, and the data that flows through that system is known as system design.
Some key features regarding the system design are-
It is intended to meet unique objectives and needs of a company or group by creating a cohesive and well-functioning system.The systematic approach to system design is implied by the term systems design. It may take a bottom-up as well as top-down approach, but in either case, the process is systematic in that it considers all associated factors of the system that must be created—from the architecture to the necessary hardware and software, all the way down to the data and in how it travels as well as transforms throughout its journey through the system.To know more about the system design, here
https://brainly.com/question/7509258
#SPJ4
Using an integrating factor, solve y-y-5 CD- in the method for solving a first-order linear differential equation, the first step is to put the equation in the standard form y alty bit). is the given equation in the standard form? No Yes Identify a(t) and bit)
Answers
The value of a(t) is -1 and b(t) is 55 + \(e^t\)
No, the given equation y' - y = 55 + \(e^t\) is not in the standard form of a first-order linear differential equation.
In the method for solving a first-order linear differential equation, an integrating factor is a function used to transform the equation into a form that can be easily solved.
For an equation in the standard form y' + a(t)y = b(t), the integrating factor is defined as:
μ(t) = e^∫a(t)dt
To solve the equation, you multiply both sides of the equation by the integrating factor μ(t) and then simplify. This multiplication helps to make the left side of the equation integrable and simplifies the process of finding the solution.
To put it in standard form, we need to rewrite it as y' + a(t)y = b(t).
Comparing the given equation with the standard form, we can identify:
a(t) = -1
b(t) = 55 + \(e^t\)
Therefore, The value of a(t) is -1 and b(t) is 55 + \(e^t\)
Learn more about integrating factor here
https://brainly.com/question/32554742
#SPJ4
Can somone answer my question please: 3cm squared onverted to 100mm squared = 300cm squared?
Answers
Answer:
hi you can solve this sum by 4×side formula
Step-by-step explanation:
plz solve and check you equation
10000mm < 90000cm
10000mm < 900000mm
help with q7 please !!

Answers
Step-by-step explanation:
\( \frac{dA}{dx} = 3 {(x - 1)}^{2} \\A = ∫3 {(x - 1)}^{2}dx \\ = ∫3 {x}^{2} - 6x + 3 \: dx \\ = \frac{3 {x}^{3} }{3} - \frac{6 {x}^{2} }{2} + 3x + c \\ = {x}^{3} - 3 {x}^{2} + 3 + c\)
Now substitute in A=10 and X=3, to find the value of c
\(10 = {3}^{3} - 3 {(3)}^{2} + 3(3) + c \\ c = 1\)
Hence,
\(A = {x}^{3} - 3 {x}^{2} + 3x + 1\)
Solve | x² + x−2 = x+3 algebraically. {Note: your text may refer to this method as the definition of absolute value, which is more commonly called the absolute value principal.} b) Verify your solution(s). c) Write your solution set { }:
Answers
The solution set is empty: {}. To solve the equation |x² + x - 2| = x + 3, we can consider two cases: when the expression inside the absolute value is positive, and when it is negative. Let's solve each case separately:
Case 1: x² + x - 2 is positive (x² + x - 2 > 0):
To find the values of x that satisfy this inequality, we can factorize the quadratic expression:
x² + x - 2 = (x + 2)(x - 1)
For the expression to be positive, both factors must have the same sign. Considering the signs of each factor:
(x + 2) > 0 => x > -2
(x - 1) > 0 => x > 1
Since both factors must be positive, we can take the intersection of the two intervals: x > 1.
Case 2: x² + x - 2 is negative (x² + x - 2 < 0):
Again, factorizing the quadratic expression:
x² + x - 2 = (x + 2)(x - 1)
For the expression to be negative, the factors must have opposite signs. Considering the signs of each factor:
(x + 2) < 0 => x < -2
(x - 1) > 0 => x > 1
Since the factors have opposite signs, we can take the union of the two intervals: x < -2 or x > 1.
Combining the solutions from both cases, we have:
x > 1 or x < -2
Now let's verify the solutions by substituting them back into the original equation:
For x > 1:
|x² + x - 2| = x + 3
Substituting x = 2:
|2² + 2 - 2| = 2 + 3
|4 + 2 - 2| = 5
|4| = 5
4 = 5 (Not true)
For x < -2:
|x² + x - 2| = x + 3
Substituting x = -3:
|-3² - 3 - 2| = -3 + 3
|-9 - 3 - 2| = 0
|-14| = 0
14 = 0 (Not true)
Since neither solution satisfies the equation, there are no valid solutions to the equation |x² + x - 2| = x + 3.
Therefore, the solution set is empty: {}
Learn more about absolute value here:
https://brainly.com/question/17360689
#SPJ11
Find the magnitude of the vector.
17i – 39j
Answers
Write two solution points for the equation y=3x-1 when x us 1 and x is 2
Answers
Answer:
x=1. (1, 2)
x=2. (2, 5)
Step-by-step explanation:
i hope this helps :)
hey can anyone help?

Answers
Answer:
23 =x
Step-by-step explanation:
The exterior angle is equal to the sum of the opposite interior angles
132 = x+109
132 -109 = x
23 =x
Answer:
x = 23°
Step-by-step explanation:
Now we have to,
→ find the required value of x.
Let's solve for value of x,
→ x + 109° = 132°
→ x = 132° - 109°
→ [ x = 23° ]
Thus, the value of x is 23°.
Can someone please answer this ? * will mark as brainiest *

Answers
Answer:
pq= 12 cm
Step-by-step explanation:
I believe PQ would be 12 cm.
The domain (Graphically)?

Answers
Answer:
Domain: (-infinite, -8) U (-8, 2) U (2, +infinite)
Step-by-step explanation:
The graphs never intersect with the lines x=-8 and x=2 so -8 and 2 cannot be included in the domain.
Use "[]" for included and "()" for excluded.
The domain will go from far left to -8 => (-infinite, -8).
Then, the domain will go from -8 to 2 => (-8, 2).
Last, the domain will go from 2 to +infinite => (2, +infinite).
in a certain group of students, the probability of a randomly chosen students being male is 40%, the probability of the students studying in Spanish is 18%, and the probability of the student being male who study Spanish is 5%. What's the probability of the student studying Spanish, if you know the students male?

Answers
Divide the 5% of Spanish by 40% male:
0.05 / 0.40 = 0.125
Change to a percent by multiplying by 100:
0.125 x 100 = 12.5%
The answer is a. 12.5%
The probability of the student studying Spanish, if you know the students male will be 12.5%.
What is probability?Probability is defined as the ratio of the number of favorable outcomes to the total number of outcomes in other words the probability is the number that shows the happening of the event.
Probability = Number of favorable outcomes / Number of sample
Given that in a certain group of students, the probability of a randomly chosen student being male is 40%, the probability of the students studying Spanish is 18%, and the probability of the student being male who studies Spanish is 5%.
The probability of the student studying Spanish, if you know the student male will be calculated as below:-
Divide the 5% of Spanish by 40% of males:
0.05 / 0.40 = 0.125
Change to a percent by multiplying by 100:
0.125 x 100 = 12.5%
Therefore, the probability of the student studying Spanish, if you know the students male will be 12.5%.
To know more about probability follow
https://brainly.com/question/24756209
#SPJ2
The mean exam score for 49 male high school students is 239 and the population standard deviation is 47 The mean exam score for 53 female high school students is 21.1 and the population standard deviation is 4.3. At α=001, can you reject the claim that male and female high school students ha equal exam scores? Complete parts (a) through (e). Click here to view page 1 of the standard normal distribution table. Click here to view. page 2 of the standard normal distribution table. A. Male high school students have lower exam scores than female students B. Male and temale high school students have different exam scores. C. Male and female high school students have equal exam scores D. Male high school students have greater exam scores than female students
Answers
Comparing the means of the two samples, we find that the difference between the means is significant. Therefore, we can reject the claim and conclude that male and female high school students have different exam scores.
To perform the two-sample t-test, we first calculate the standard error of the difference between the means using the formula:
SE = sqrt((s1^2 / n1) + (s2^2 / n2))
Where s1 and s2 are the population standard deviations of the male and female students respectively, and n1 and n2 are the sample sizes. Plugging in the values, we have:
SE = sqrt((47^2 / 49) + (4.3^2 / 53))
Next, we calculate the t-statistic using the formula:
t = (x1 - x2) / SE
Where x1 and x2 are the sample means. Plugging in the values, we have:
t = (239 - 21.1) / SE
We can then compare the t-value to the critical t-value at α = 0.01 with degrees of freedom equal to the sum of the sample sizes minus 2. If the t-value exceeds the critical t-value, we reject the null hypothesis.
In this case, the t-value is calculated and compared to the critical t-value using the provided standard normal distribution table. Since the t-value exceeds the critical t-value, we can reject the claim that male and female high school students have equal exam scores.
Therefore, the correct answer is:
B. Male and female high school students have different exam scores.
Learn more about hypothesis testing here: brainly.com/question/17099835
#SPJ11