what two requirements do you need for the chi square goodness of fit test
Answers
Answer:
Data values that are a simple random sample from the full population.
Categorical or nominal data. The Chi-square goodness of fit test is not appropriate for continuous data.
A data set that is large enough so that at least five values are expected in each of the observed data categories.
Related Questions
Solving Inequalities with One Variable
Show work
2(7 − 2) > 9 + 6
Answers
Answer: no solution
Step-by-step explanation:
2× (7-2)>9+6
Calculate the sum or difference
2×5>9+6
Calculate the sum or difference
2 × 5 > 15
2×5>15
Calculate the product or quotient
10 > 15
10 > 15
The solution of the inequality
no solution
The angle measures of triangle ABC are given:
The measure of angle A is (2x−10)°.
The measure of angle B is 70°.
The measure of angle C is (4x)°.
What is the value of x?
Enter your answer in the box.
x =
Answers
Answer:
x=20
Step-by-step explanation:
By the Triangle Sum Theorem, the angles of a triangle add up to 180. So we can set up the equation like this:
2x-10+70+4x=180
Combine Like terms
6x+60=180
Subtract 60 from both sides
6x=120
Divide by 6 to isolate the variable
x=20
Answer:x= 20
Step-by-step explanation:
As the equation of three angles of a triangle is 180°,
Then, 2x-10+70+4x=180
6x=120
So,x= 20
What is the volume of the square pyramid?

Answers
Answer:
\( \frac{1}{3} ( {21}^{2} ) \sqrt{ {23}^{2} - {10.5}^{2} } \)
\( = 3008.1\)
The volume of this square pyramid is about 3,008.1 mm^2.
Let X₁, X₂, X₃, ... be i.i.d. variables taking values between +1 and +[infinity] with probability density given by:
f(x) = (λ - 1)/x^λ
for every x ≥ 1 where λ > 1 is an unknown parameter. For x < 1, we assume the probability density to be 0. Estimate λ using maximum likelihood, given X₁ = 3, X₂ = 4, X₃ = 5
Answers
To estimate the unknown parameter λ using maximum likelihood, given X₁ = 3, X₂ = 4, X₃ = 5, we need to find the value of λ that maximizes the likelihood function based on the observed data. The likelihood function represents the probability of observing the given data for different values of λ.
The likelihood function L(λ) is defined as the product of the probability density function evaluated at each observed data point. In this case, we have L(λ) = f(3) * f(4) * f(5), where f(x) is the given probability density function.
Substituting the values into the likelihood function, we have L(λ) = ((λ - 1)/3^λ) * ((λ - 1)/4^λ) * ((λ - 1)/5^λ).
To find the maximum likelihood estimate of λ, we need to maximize the likelihood function. Taking the natural logarithm of the likelihood function (ln L(λ)), we can simplify the problem to finding the value of λ that maximizes ln L(λ).
Taking the derivative of ln L(λ) with respect to λ and setting it to zero, we can solve for the maximum likelihood estimate of λ.
By solving the equation, we can obtain the estimate for λ based on the observed data X₁ = 3, X₂ = 4, X₃ = 5.
learn more about probability here
https://brainly.com/question/30034780
#SPJ11
A garden table and a bench cost $746 combined. The garden table costs $46 more than the bench. What is the cost of the bench?
Answers
Answer: The bench would cost about 396$
hope I helped you :D
Answer:
the bench costs $350
Step-by-step explanation:
Let's assume cost of table be T and bench be B
therefore, T+B= 746 ...........(1)
while we are given T= B+46 ............(2)
using (2) in (1)
[B+46] + B =746
2B= 700
B=350
So, cost of bench= $350
The mean of 30 numbers is 18. What will be the new mean, if each observation is
increased by 2.
Answers
Answer:
The new mean will be 20.
Step-by-step explanation:
The Mean Value of a Data Set
The mean or average of a data set is found by adding all numbers and then dividing by the number of values in the set. Written as a formula:
\(\displaystyle \bar x=\frac{\sum x_i}{n}\)
Where xi is the value of each data and n is the total number of values.
The mean of n=30 numbers is \(\bar x=18\). If each observation is increased by 2, then xi'=xi+2 and the new mean value will be:
\(\displaystyle \bar x'=\frac{\sum x'_i}{30}\)
\(\displaystyle \bar x'=\frac{\sum x_i+2}{30}\)
\(\displaystyle \bar x'=\frac{\sum x_i}{30}+\frac{\sum 2}{30}\)
The sum of 30 times 2 is 60, thus:
\(\displaystyle \bar x'=18+\frac{60}{30}=18+2=20\)
The new mean will be 20.
Your mother gave you $15.80 with which
to buy a present. This covered of the
2
3
cost. How much did the present cost?
Answers
Answer: it cost 14 dollars
Step-by-step explanation:
In two years, the value of a car changed from $14,000 to $11,200.What is the percent of change
Answers
Answer:
Percentage change = (14000-11200) / 11200 * 100
= 280000 / 11200
= 25%
So, your final answer is 25%
Hope this helps!
Step-by-step explanation:
Which points lie on the graph of f(x) = log9x?-1/81, 20,11/9, -13, 2439,181,2
Answers
The points on the graph of f(x) = log9x are (20, 4.5), (11/9, 0.087183), (2439, 3.168910), (181, 2.55231), and (2, 1).
The points on the graph of f(x) = log9x can be calculated by substituting the given values of x in the equation. For example,
f(-1/81) = log9(-1/81) = log9(-1) - log9(81) = undefined
f(20) = log9(20) = log9(2*2*2*5) = log9(2) + log9(2) + log9(2) + log9(5) = 1 + 1 + 1 + 1.5 = 4.5
f(11/9) = log9(11/9) = log9(11) - log9(9) = 1.041393 - 0.954210 = 0.087183
f(-13) = log9(-13) = log9(-1) - log9(13) = undefined
f(2439) = log9(2439) = log9(3*13*37) = log9(3) + log9(13) + log9(37) = 0.477121 + 1.11394 + 1.579789 = 3.168910
f(181) = log9(181) = log9(3*3*7*7) = log9(3) + log9(3) + log9(7) + log9(7) = 0.477121 + 0.477121 + 0.84509 + 0.84509 = 2.55231
f(2) = log9(2) = log9(2) = 1
Hence, the points on the graph of f(x) = log9x are (20, 4.5), (11/9, 0.087183), (2439, 3.168910), (181, 2.55231), and (2, 1).
Learn more about points on the graph here:
https://brainly.com/question/29253202
#SPJ4
H=
And the equation
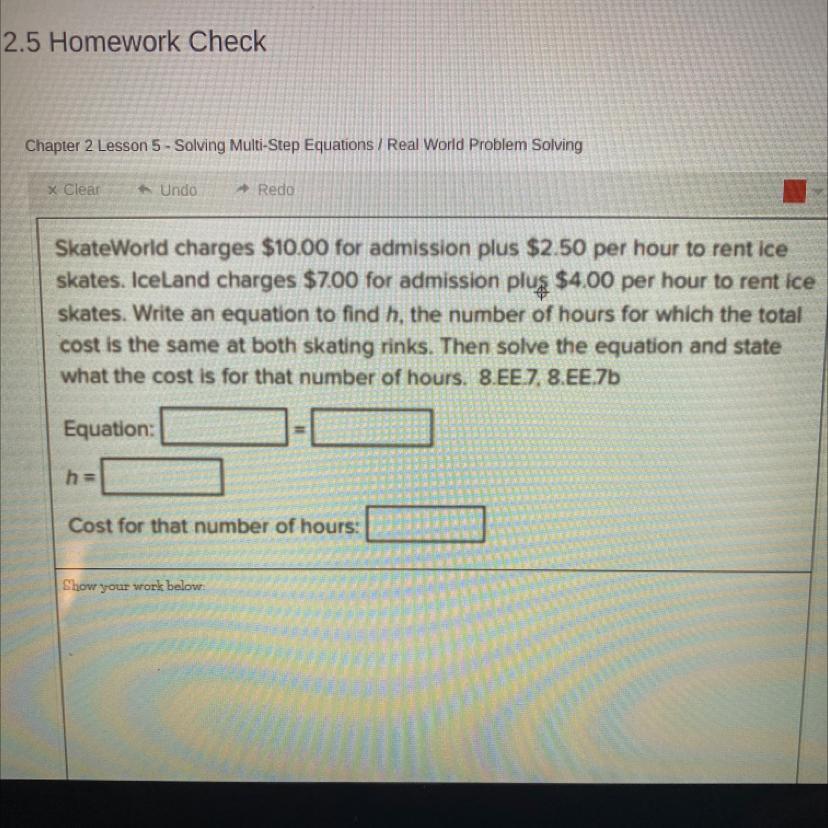
Answers
Answer:
equation: 10.00+2.50h=7.00+4.00h
10+2.5h-4h=7
10-1.5h=7
-1.5h=7-10
1.5h/1.5=-3/1.5
h=2
the z value for a 97.8% confidence interval estimation is
Answers
The z value for a 97.8% confidence interval estimation is determined as 2.29.
What is the z value for a 97.8% confidence?The z value for a 97.8% confidence interval estimation is calculated as follows;
The find the Z score, go to a Z lookup table which is found in a textbook or on an internet source. z table is created to give the possibility in a one-tailed analysis.
A confidence interval is a two-tailed examination, in order to prepare the z score for 97.8%, look up the probability of 98.9%.
The value of 98.9% is
= (0.978 + 1 )/ 2
= 0.989 or 98.9%.
This implies that the z score of the date is 2.29.
Learn more about z-score here: https://brainly.com/question/28000192
#SPJ1
a service center receives an average of 0.5 customer complaints per hour. management's goal is to receive fewer than three complaints each hour. assume the number of complaints follows the poisson distribution. determine the probability that at most three complaints will be received during the next four hours.
Answers
the probability that at most 3 complaints will be received during the next 4 hours is 0.2381 or approximately 23.81%.
Let X be the number of complaints received in 4 hours. Then X follows a Poisson distribution with mean λ = 0.5 complaints/hour × 4 hours = 2 complaints.
To find the probability that at most 3 complaints will be received during the next 4 hours, we can use the Poisson probability formula:
P(X ≤ 3) = e^(-λ) * [λ^0/0! + λ^1/1! + λ^2/2! + λ^3/3!]
P(X ≤ 3) = e^(-2) * [1/1 + 2e^(-2)/1! + 4e^(-2)/2! + 8e^(-2)/3!]
P(X ≤ 3) = 0.2381
what is number?
A number is a mathematical object used to quantify and measure things. It can be used to represent quantities such as size, amount, distance, time, and many other things. Numbers can be integers, fractions, decimals, or irrational numbers, and they can be positive, negative, or zero. In mathematics, numbers are used to perform calculations and solve problems in various fields such as science, engineering, economics, and more.
To learn more about probability visit:
brainly.com/question/32117953
#SPJ11
Need answers with explanation

Answers
Step-by-step explanation:
i guess it helps..if yuh need step by step explanation.comment i try to explain in worda

Nicholas bought 24feet of fabric at afabric store. The fabric cost $1.35 per foot, including sales tax. If Nicholaspaid with a $50bill, how much change should he have received?
Answers
Answer:
24x1.35=32.4
He should have recieved $32.40 in change.
Question 5 of 10
Which pair of functions are inverses of each other?
O A. f(x) = 2 + 15 and g(x) = 12x - 15
O B. f(x) = √3x and g(x) = () ³
O c. f(x) = 3 - 10 and g(x) = +10
3
D. f(x) = 11x-4 and g(x) = +4

Answers
The correct answer is D. f(x) = 11x - 4 and g(x) = (x + 4)/11
To determine which pair of functions are inverses of each other, we need to check if the composition of the functions results in the identity function, which is f(g(x)) = x and g(f(x)) = x.
Let's test each option:
Option A:
f(x) = x/2 + 15
g(x) = 12x - 15
f(g(x)) = (12x - 15)/2 + 15 = 6x - 7.5 + 15 = 6x + 7.5 ≠ x
g(f(x)) = 12(x/2 + 15) - 15 = 6x + 180 - 15 = 6x + 165 ≠ x
Option B:
f(x) = ∛3x
g(x) = (x/3)^3 = x^3/27
f(g(x)) = ∛3(x^3/27) = ∛(x^3/9) = x/∛9 ≠ x
g(f(x)) = (∛3x/3)^3 = (x/3)^3 = x^3/27 = x/27 ≠ x
Option C:
f(x) = 3/x - 10
g(x) = (x + 10)/3
f(g(x)) = 3/((x + 10)/3) - 10 = 9/(x + 10) - 10 = 9/(x + 10) - 10(x + 10)/(x + 10) = (9 - 10(x + 10))/(x + 10) ≠ x
g(f(x)) = (3/x - 10 + 10)/3 = 3/x ≠ x
Option D:
f(x) = 11x - 4
g(x) = (x + 4)/11
f(g(x)) = 11((x + 4)/11) - 4 = x + 4 - 4 = x ≠ x
g(f(x)) = ((11x - 4) + 4)/11 = 11x/11 = x
Based on the calculations, only Option D, where f(x) = 11x - 4 and g(x) = (x + 4)/11, satisfies the condition for being inverses of each other. Therefore, the correct answer is:
D. f(x) = 11x - 4 and g(x) = (x + 4)/11
for such more question on inverses
https://brainly.com/question/15066392
#SPJ8
A vase contains 60 marbles, all of which are red or orange. if the ratio of red marbles to orange ones is 1:5, what is the total number of red marbles in the vase?
Answers
The total number of red marbles in the vase are 10.
What is the ratio?A ratio is described as a comparison between two amounts with the same unit to determine the amount of 1 quantity is contained in the other. Ratios are divided into two sorts.
The first is a part-to-part ratio, and the second is a part-to-whole ratio. The part-to-part ratio expresses the relationship between 2 separate entities or groupings.
Now, according to the question;
Let 'x' be the red marbles in the vase.
Let 'y' be the orange marbles in the vase.
The total number of marbles in the vase are 60
x + y = 60 (equation 1)
The ratio of red marbles to orange ones is 1:5.
Thus, x/y = 1/5
cross multiplying;
5x = y
or y = 5x
substitute the value of y in equation 1;
x + y = 60 (equation 1)
x + 5x = 60
6x = 60
x = 10 (red marbles)
Thus, the number of red marbles in the vase are 10.
To know more about the ratio, here
https://brainly.com/question/25927869
#SPJ4
nancy goes fishing with Jason. they catch 14 trout if they equally split up trout how many will each one get
Answers
Answer:
They will each get 7 trout.
Step-by-step explanation:
Since there are two people (Nancy and Jason), take the 14 trout, and divide it amongst the two, so, they each get 7 fish.
What is the x-intercept of the line graphed on the grid?

Answers
Answer:
2
Step-by-step explanation:
If you use rise over run, you should get to. From one point to the other, the rise is 2 and the run to the right is 1. So, you do 2 divided by 1, which is 2. So, the slope would be 2.
choose the statement that is false.group of answer choicesa 95% confidence interval is wider than a 90% confidence intervalwhen sampling for means and thinking about the central limit theorem, the n should always be >30.when estimating the standard deviation in calculating confidence intervals, make sure you use the t tables.reducing the variation of a process will increase the width of a given confidence interval relative to that process.
Answers
Reducing the variation of a process will increase the width of a given confidence interval relative to that process.
Option C is correct .
What is a confidence interval?
In statistics, the probability that a population parameter will fall between a set of values for a predetermined percentage of the time is referred to as a confidence interval. By employing the dimensions of values used in the computation of the intervals, it is simple to establish the link between components of two confidence intervals. The width is a fundamental component in these range estimates, which are affected by sample size, etc.
Hence, reducing the variation of a process will increase the width of a given confidence interval relative to that process is false.
To learn more about confidence interval :
brainly.com/question/17212516
#SPJ4
expand each logarithm

Answers
Hence, log(sqrt(3.5.11),9) in its enlarged version is roughly similar to 0.2148. We may answer this question by using the definition of logrithmic.
Describe logrithmic.Mathematical operations that relate to a number's logarithm are known as logarithmic functions. The power that a given basis must be increased in order to obtain a particular number is known as the logarithm of the number.
Although 10 (also known as the common logarithm) is the base that is most frequently used, logarithms can be calculated in relation to any positive base higher than 1. If the base is 10, the logarithm of such an integer x with regard to a base b is written by log(base b)(x), or just log(x).
We can compress the given logarithm via the logarithmic identity log(base a)(bc) = c * log(base a)(b):
Sqrt(3.5.11) = Log((3.5.11)(1/2), 9) = Log((3.5.11)*(1/2), 9) = (1/2) * Log (3.5.11, 9)
We must now calculate that logarithm of 9 in base 3.5.11. This can be changed to a log with a more recognisable column, such as base 10 or base e, using the change-of-base formula. Using the base 10 scale
3.5.11, 9) = 9)/log (3.5.11)
We can calculate this using a calculator:
log(9) = 0.9542 (reduced to 4 decimal places)
log(3.5.11) = log(3) + log(5) + log(11) = 0.4771, 0.6978, and 1.0414, respectively, yielding 2.2174. (rounded to 4 decimal places)
Therefore:
sqrt(3.5.11),9 = (1/2) log(3.5.11,9) = (1/2) log(9)/log(3.5.11)) = (1/2) log(0.9542/2.2174) = 0.2148 log(3.5.11,9) = (1/2) log(3.5.11, 9) = (1/2)
Hence, log(sqrt(3.5.11),9) in its enlarged version is roughly similar to 0.2148.
To know more about log visit;
https://brainly.com/question/28596588
#SPJ1
The expanded form of the logarithm is:
log base 9 √(3.5.11) = log base 9 (3) + log base 9 (5) + log base 9 (11)
What is logarithm?
A logarithm is a mathematical function that tells us what exponent is needed to produce a given number, when that number is expressed as a power of a fixed base. In other words, logarithms tell us how many times we need to multiply the base by itself to get the desired number.
We can use the property of logarithms that says:
log base b (a * c) = log base b (a) + log base b (c)
to expand the logarithm.
Therefore, we have:
log base 9 √(3.5.11) = log base 9 √(3 * 5 * 11)
= log base 9 (3) + log base 9 (5) + log base 9 (11)
So, the expanded form of the logarithm is:
log base 9 √(3.5.11) = log base 9 (3) + log base 9 (5) + log base 9 (11)
To learn more about logarithm from the given link:
https://brainly.com/question/30085872
#SPJ1
Given that f(x) = x^2 - 6x + 8 and g(x) = x – 2, find (f.g)(x) and express
the result in standard form.
Answers
Answer:
(F.g(x))=x^2-10x+24
Step-by-step explanation:
when when we have a composition function, like f of g of x, we put the second function g of x in place of every x in f of x,
so f(x)=x^2-6x+8
and we will put x-2 which is g(x) in the place of every x
so f(g(x))=(x-2)^2-6(x-2)+8
so we ca n simplify that into f(g(x))=x^2-4x+4-6x+12+8
which simplifies to f(g(x))=x^2-10x+24
Determine if you can use the HL ! Congruence Theorem to prove triangle ABC cong triangle DCB If not, tell what else you need to know

Answers
Answer: Yes you can use the HL theorem
Explanation:
HL = hypotenuse leg
The tickmarks tell us about the congruent hypotenuse sides. This takes care of the "H" from "HL".
The "L" portion is because BC = BC (reflexive property) which are the congruent legs.
So we have enough info to use the HL theorem to prove the triangles are congruent.
Note: The HL theorem only works for right triangles.
Which inequality is shown in the graph below.

Answers
George's scale drawing of a rectangular volleyball court is 6 inches long
by 3 inches wide. What is the
actual area if the scale is 1 inch = 8 meters?
Answers
Second time posting this. Please help!! :)

Answers
Answer:
Step-by-step explanation:
\(\frac{480+24(x-40)}{x}\)
The numerator of the rational expression the money he earned for 'x' hours
The rate at which William is paid for each hour in excess of 40 hours 24.
x = 50 hours = (40 + 10 ) hours
The amount paid for excess 10 hours = 24 *10 = 240
Total amount earned for the week = 480 + 240 = 720
yuki works at a garden store. She is stacking 40 pound bags. what is the total weight of 5 bags of soil
Answers
Answer:
w=40b
Step-by-step explanation:
Answer:
200
Step-by-step explanation:
You multiply 40 by 5.
solve -36 = x over 9
Answers
Answer:
x = -324
Step-by-step explanation:
\( - 36 = \frac{x}{9} \\ - 36 \times 9 = \frac{x}{9} \times 9 \\ - 324 = x\)
If A= 1, Be= 7, then ADD=?
Answers
Answer:
D or DD was not given any factor, but A was given which is 1, ADD= 1 multipltied by D
The set W is a subset of set of real numbers R cubed. If W were a vector space, what else would be true about it?
A. The set W would be the null space of any matrix A that can be broken up into vectors that span set of real numbers R cubed.
B. The set W has at least one basis with each dimension from 0 to 3, inclusive.
C. The set W would not contain the zero vector for set of real numbers R cubed.
D. The set W would be a subspace of set of real numbers R cubed.
Answers
D. The set W would be a subspace of set of real numbers R cubed.
For a set to be considered a vector space, it must satisfy the following conditions:
1. It contains the zero vector (the additive identity).
2. It is closed under vector addition.
3. It is closed under scalar multiplication.
Since the set W is a subset of R cubed, it inherits the properties of R cubed, including the zero vector. Therefore, option C is not true.
Options A and B are not necessarily true for all subsets of R cubed. They may hold for some specific subsets, but they are not general properties that apply to all subsets.
Option D is the correct answer because it states that the set W would be a subspace of R cubed. A subspace is a subset of a vector space that is itself a vector space, satisfying all the properties of a vector space. Since W is a subset of R cubed, it would be a subspace if it satisfies the three conditions mentioned above.
To know more about vector visit:
brainly.com/question/24256726
#SPJ11
rove the following identity for any positive n≥1 ∑
i=1
n
∑
j=1
i
2=n(n+1) 2. Solve the following recurrence and prove the solution correct by induction:
T(1)
T(n)
=4c
=2cn+T(n/2).
3. You are given the function g(n)=nlogn. for each function f(n) below prove or disprove that f(n)=O(g(n)) a) f(n)=3n
2
b) f(n)=4n c) f(n)=6nlogn+5n d) f(n)=(logn)
2
Answers
a) f(n) = 3n^2 is not O(g(n))
b) f(n) = 4n is O(g(n))
c) f(n) = 6nlog(n) + 5n is O(g(n))
d) f(n) = (log(n))^2 is not O(g(n))
1. Proof of the identity ∑[i=1 to n] ∑[j=1 to i] 2 = n(n+1)/2:
Let's evaluate the double sum on the left-hand side:
∑[i=1 to n] ∑[j=1 to i] 2
We can rewrite this as:
∑[i=1 to n] (2i)
Now, let's simplify the right-hand side of the equation:
n(n + 1)/2
Expanding the expression, we get:
\((n^2 + n)/2\)
To prove the identity, we need to show that the double sum on the left-hand side is equal to the expression on the right-hand side.
Let's evaluate the double sum:
∑[i=1 to n] (2i) = 2(1) + 2(2) + ... + 2(n)
Using the formula for the sum of an arithmetic series, we have:
∑[i=1 to n] (2i) = 2(1 + 2 + ... + n) = 2[(n(n + 1))/2] = n(n + 1)
We have shown that the left-hand side is equal to n(n + 1), which matches the expression on the right-hand side. Therefore, the identity is proven.
2. Solution to the recurrence T(1) = 4c, T(n) = 2cn + T(n/2):
To solve the recurrence relation, we can use the method of recursion tree and prove the solution by induction.
Step 1: Guess the solution: We assume that the solution to the recurrence relation is T(n) = knlogn for some constant k.
Step 2: Base case: T(1) = 4c (given). Plugging in n = 1 in the assumed solution, we have:
T(1) = k(1)log(1) = k(0) = 4c
From this, we can deduce that k = 4c.
Step 3: Inductive step: Assume that the solution holds for T(n/2), i.e., T(n/2) = (4c)(n/2)log(n/2).
Now, let's compute T(n) using the given recurrence relation:
T(n) = 2cn + T(n/2) = 2cn + (4c)(n/2)log(n/2)
Simplifying further, we get:
T(n) = 2cn + 2cnlog(n/2) = 2cn(1 + log(n/2))
Using log property, we can write log(n/2) as log(n) - log(2) = log(n) - 1.
Substituting this back into the equation, we have:
T(n) = 2cn(1 + log(n) - 1) = 2cnlog(n)
We have shown that T(n) = 2cnlog(n), which matches our assumed solution.
Step 4: By induction, we have proven that the solution to the recurrence relation T(1) = 4c, T(n) = 2cn + T(n/2) is T(n) = 2cnlog(n).
3. Proving or disproving f(n) = O(g(n)) for the given functions:
a) \(f(n) = 3n^2\)
To prove or disprove f(n) = O(g(n)), we need to show that there exist constants c and n0 such that f(n) <= c * g(n) for all n >= n0.
Let g(n) = nlog(n). Let's evaluate the limit of f(n)/g(n) as n approaches infinity:
\(lim (n- > ∞) (3n^2 / (nlog(n))) = lim (n- > ∞) (3n / log(n))\)
Using L'Hôpital's rule, we differentiate the numerator and denominator:
lim (n->∞) (3 / (1/n)) = lim (n->∞) (3n) = ∞
Since the limit is not finite, we can conclude that \(f(n) = 3n^2\) is not O(g(n)).
b) f(n) = 4n
Similarly, let's evaluate the limit of f(n)/g(n) as n approaches infinity:
lim (n->∞) (4n / (nlog(n))) = lim (n->∞) (4 / log(n))
Again, using L'Hôpital's rule:
lim (n->∞) (0 / (1/n)) = lim (n->∞) (0) = 0
Since the limit is finite, we can conclude that f(n) = 4n is O(g(n)).
c) f(n) = 6nlog(n) + 5n
Evaluating the limit:
lim (n->∞) ((6nlog(n) + 5n) / (nlog(n))) = lim (n->∞) ((6log(n) + 5) / log(n))
Using L'Hôpital's rule:
\(lim (n- > ∞) ((6 / (1/n)) / (1/n)) = lim (n- > ∞) (6) = 6\)
Since the limit is finite, we can conclude that f(n) = 6nlog(n) + 5n is O(g(n)).
d) \(f(n) = (log(n))^2\)
Evaluating the limit:
\(lim (n- > ∞) (((log(n))^2) / (nlog(n))) = lim (n- > ∞) ((2log(n)/n) / (1/n)) = lim (n- > ∞) (2log(n)) = ∞\)
Since the limit is not finite, we can conclude that \(f(n) = (log(n))^2\) is not O(g(n)).
To know more about log refer here:
https://brainly.com/question/32621120
#SPJ11