what the slope and the y intercept for-12x+4y=-8
Answers
Answer:
slope is -3
y-intercept is -2
Step-by-step explanation:
put into slope-intercept form which is y = mx + b where 'm' is slope and 'b' is the y-intercept
12x + 4y = -8
4y = -12x - 8
y = -12/4x - 8/4
y = -3x - 2 (simplified)
Related Questions
f(x)=5sinx+cosx then f ′
(x)=−5cosx−sinx Select one: True False
Answers
False. The derivative of the function f(x) = 5sin(x) + cos(x) is not equal to -5cos(x) - sin(x). The correct derivative of f(x) can be obtained by applying the rules of differentiation.
To find the derivative, we differentiate each term separately. The derivative of 5sin(x) is obtained using the chain rule, which states that the derivative of sin(u) is cos(u) multiplied by the derivative of u. In this case, u = x, so the derivative of 5sin(x) is 5cos(x).
Similarly, the derivative of cos(x) is obtained as -sin(x) using the chain rule.
Therefore, the derivative of f(x) = 5sin(x) + cos(x) is:
f'(x) = 5cos(x) - sin(x).
This result shows that the derivative of f(x) is not equal to -5cos(x) - sin(x).
In summary, the statement that f'(x) = -5cos(x) - sin(x) is false. The correct derivative of f(x) = 5sin(x) + cos(x) is f'(x) = 5cos(x) - sin(x).
To learn more about derivative, click here: brainly.com/question/23819325
#SPJ11
NEED HELP PLEASE.
4(x-3)=20
Answers
Answer: x = 8
Step-by-step explanation:
Distribute the 4 into (x - 3). The new equation should be 4x - 12 = 20.Add 12 on both sides. The new equation is 4x = 32.Divide 4 on both side. The solution is x = 8.Find the equation of the straight line passing through the point (3,5) which is perpendicular to the line y=3x+2
Answers
Answer:
the desired equation is y = (-1/3)x + 6
Step-by-step explanation:
Let the given line be A: y=3x+2
The slope of line A is m = 3.
The slope of any line B which is perpendicular to line A is the negative reciprocal of the slope of A: m = -(1/3).
The particular perpendicular line that passes through (3, 5) is then
5 = (-1/3)(3) + b, which simplifies to 5 = -1 + b, or b = 6.
Thus, the desired equation is y = (-1/3)x + 6
Complete the equation of this circle:
A
1
[ ]=z([_]_^)+z([ ¿ ] − x)
Enter ⚠️NEED HELP ASAP WILL GIVE BRAINLIEST⚠️
![Complete the equation of this circle:A1[ ]=z([_]_^)+z([ ] x)Enter NEED HELP ASAP WILL GIVE BRAINLIEST](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/B9Zoj6FUdD0MnfMIGhrzlEdfSSDG1g9X.png)
Answers
Answer:
(x - 3)^2 + (y - 2)^2 = 4^2
Step-by-step explanation:
Looking at the graph its obviously a circle as it said.
We have to find (h,k) and the radius of that circle.
(h, k) = (3,2)
Origin to the edge of the A.
radius = 4
(x - 3)^2 + (y - 2)^2 = 4^2
In the figure, RV, WS, and QT intersect at point P.
What is the value of x? Show your work.
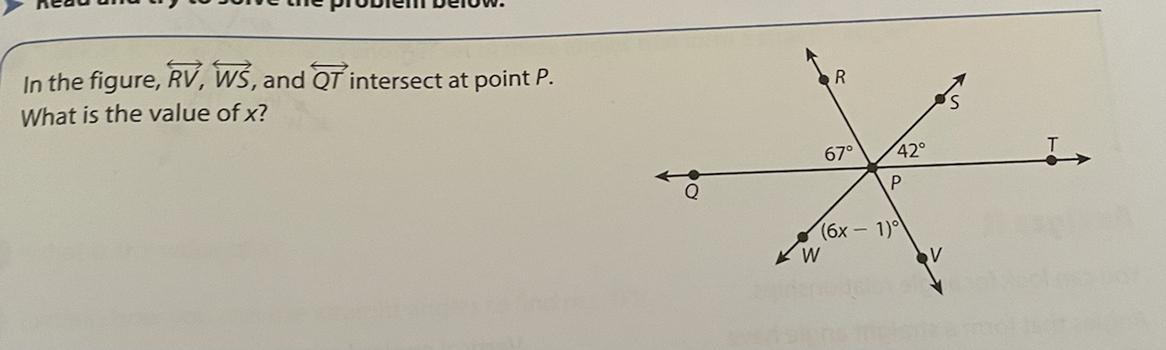
Answers
Answer:
x = 12
Step-by-step explanation:
67+42+6x-1=180
108+6x=180
6x=72
x=12
given a set of data and a corresponding regression line, describe all values of x that provide meaningful predictions for y. a. prediction value are meaningful for all x-values that are realistic in the context of the original data setb. prediction value are meaningful only for x-values that are not included in the original data setc. prediction value are meaningful only for x-values in (or close to) the range of the original data
Answers
Once the regression line has been constructed, it can be used to make predictions about the value of y for a given value of x. However, these predictions are only meaningful if the value of x is in or close to the range of the original data. This is because the regression line is constructed based on the data points, and therefore it only accurately models the relationship between x and y within the range of the data.
For example, if the original data points have x-values between 0 and 100, then the regression line will provide meaningful predictions for y only for x-values between 0 and 100, or close to this range. Predictions for x-values outside of this range may not be accurate, because the regression line may not accurately represent the relationship between x and y outside of the range of the data.
Therefore, in order for the prediction value to be meaningful, the value of x must be in or close to the range of the original data.
describe the graph of the solution

Answers
First, we want to note two things:
We have a solid circle at -10, so -10 IS part of the solution.We have shading to the right of -10, meaning we also need to include numbers to the right of -10, or numbers greater than -10.
We can describe this with an inequality: x ≥ -10
Be sure you use ≥ and not >, since -10 is included.
We can describe this with interval notation: [ -10, infty )
Be sure you use [ and not ( on -10, since -10 is included.
You can also use set-builder notation: { x | x ≥ -10 }
Solve for x. Round to the nearest tenth,if necessary.

Answers
The value of x is approximately 0.8 cm when rounded to the nearest tenth.
Describe Triangle?A triangle is a two-dimensional geometric shape that has three sides and three angles. It is the simplest polygon and is a fundamental building block in many areas of mathematics and science.
The three sides of a triangle can have different lengths and can be of different types, such as equilateral, isosceles, or scalene. An equilateral triangle has three sides of equal length, while an isosceles triangle has two sides of equal length and a third side of a different length. A scalene triangle has all three sides of different lengths.
In a right triangle, the sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. Thus, we have:
sin(IHJ) = IJ/IH
Taking the sine of both sides and substituting the given values, we get:
sin(23°) = x/2
Multiplying both sides by 2, we have:
x = 2*sin(23°)
Using a calculator, we get:
x ≈ 0.83
Therefore, the value of x is approximately 0.8 cm when rounded to the nearest tenth.
To know more about calculator visit:
https://brainly.com/question/18481378
#SPJ1
Use the elimination method to find a general solution for the given linear system, where differentiation is with respect to t. 2x' y'-4x-4y=e^-t x' y' 2x y=e^4t
Answers
It looks like the system of ODEs is
\(\begin{cases} 2x' + y' - 4x - 4y = e^{-t} \\ x' + y' + 2x + y = e^{4t} \end{cases}\)
Differentiate both sides of both equations with respect to \(t\).
\(\begin{cases} 2x'' + y'' - 4x' - 4y' = -e^{-t} \\ x'' + y'' + 2x' + y' = 4e^{4t} \end{cases}\)
Eliminating the exponential terms, we have
\((2x' + y' - 4x - 4y) + (2x'' + y'' - 4x' - 4y') = e^{-t} + (-e^{-t}) \\\\ \implies (2x'' - 2x' - 4x) + (y'' - 3y' - 4y) = 0\)
\((x'' + y'' + 2x' + y') - 4 (x' + y' + 2x + y) = 4e^{4t} - 4\cdot e^{4t} \\\\ \implies (x'' - 2x' - 8x) + (y'' - 3y' - 4y) = 0\)
Now we can eliminate \(y\) and it derivatives.
\(\bigg((2x'' - 2x' - 4x) + (y'' - 3y' - 4y)\bigg) - \bigg((x'' - 2x' - 8x) + (y'' - 3y' - 4y)\bigg) = 0 - 0 \\\\ \implies x'' + 4x = 0\)
Solve for \(x\). The characteristic equation is \(r^2 + 4 = 0\) with roots at \(r=\pm2i\), hence the characteristic solution is
\(\boxed{x(t) = C_1 \cos(2t) + C_2 \sin(2t)}\)
Solve for \(y\). Substituting \(x\) into the second ODE gives
\(x' + y' + 2x + y = e^{4t} \\\\ \implies y' + y = e^{4t} + C_1 \cos(2t) + C_2 \sin(2t)\)
The characteristic equation this time is \(r + 1 = 0\) with a root at \(r=-1\), hence the characteristic solution is
\(y(t) = C_3 e^{-t}\)
Assume a particular solution with unknown coefficients \(a,b,c\) of the form
\(y_p = ae^{4t} + b \cos(2t) + c \sin(2t) \\\\ \implies {y_p}' = 4ae^{4t} - 2b\sin(2t) + 2c\cos(2t)\)
Substituting into the ODE gives
\(5ae^{4t} + (b+2c) \cos(2t) + (-2b+c) \sin(2t) = e^{4t} + C_1 \cos(2t) + C_2 \sin(2t) \\\\ \implies \begin{cases}5a = 1 \\ b+2c = C_1 \\ -2b+c = C_2\end{cases} \\\\ \implies a=\dfrac15, b=\dfrac{C_1-2C_2}5, c=\dfrac{2C_1+C_2}5\)
so that the general solution is
\(\boxed{y(t) = \dfrac15 e^{4t} + \dfrac{C_1-2C_2}5 \cos(2t) + \dfrac{2C_1+C_2}5 \sin(2t) + C_3 e^{-t}}\)
Round each of these numbers to the degree of accuracy shown in the brackets
a) 4865
(Nearest ten)
Answers
Answer:
irst, 4865 rounded to the nearest ten is:
4870
Step-by-step explanation:
Here we will tell you what 4865 is rounded to the nearest ten and also show you what rules we used to get to the answer.
Remember, we did not necessarily round up or down, but to the ten that is nearest to 4865.
When rounding to the nearest ten, like we did with 4865 above, we use the following rules:
A) We round the number up to the nearest ten if the last digit in the number is 5, 6, 7, 8, or 9.
B) We round the number down to the nearest ten if the last digit in the number is 1, 2, 3, or 4.
C) If the last digit is 0, then we do not have to do any rounding, because it is already to the ten.
At the book store, you purchased some $3 clearance mystery books and $8 regular-priced science fiction books. How many of each did you buy if you spent a total of $77?
Answers
Answer:
we bought 12 $3 clearance mystery books and 5 $8 regular-priced science fiction books.
Step-by-step explanation:
assume you are risk-averse and have the following three choices. expected value standard deviation a $ 2,710 $ 1,070 b 2,140 1,820 c 2,160 1,130 compute the coefficient of variation for each. note: round your answers to 3 decimal places.
Answers
The coefficient of variation for a)0.394 b)0.850 c)0.523 if standard deviation values are a $ 2,710 $ 1,070 b 2,140 1,820 c 2,160 1,130
The coefficient of variation as compared to standard deviation is a factual proportion of the scattering of data of interest around the mean. The measurement is usually used to analyze the information scattering between particular series of information.
Dissimilar to the standard deviation that must continuously be viewed as with regards to the mean of the information, the coefficient of variation tells a somewhat straightforward and fast instrument to look at changed information series.
We know very well that coefficient of variation is defined as the ratio of standard deviation to the expected value, or in other words
Coefficient of variation=standard deviation/expected value
a)Standard deviation value=$1,070 and expected value is $2,710
Therefore, coefficient of variation=(1070/2710)=0.394
b)Standard deviation value=$1,820 and expected value is $2,140
Therefore, coefficient of variation=(1820/2140)=0.850
c)Standard deviation value=$1130 and expected value is $2,160
Therefore, coefficient of variation=(1130/2160)=0.523
Hence, coefficient of variation value is a)0.394 b)0.850 c)0.523
To know more about coefficient of variation, visit here:
https://brainly.com/question/13293164
#SPJ4
The length of a rectangle 10 more than twice the width, if a perimeter is 80 inches find the length and the width
Answers
Which is a solution to the system of linear
inequalities? Select all that apply.
y > 2x + 5
y<-3x+5
a. (-5, -1)
b. (0, 2)
c. (-4,1)
d. (-3,0)

Answers
write the sum in sigma notation. 3 − 3x 3x2 − 3x3 · · · (−1)n3xn
Answers
Hi! I'd be happy to help you write the sum in sigma notation. Given the sum: 3 - 3x + 3x^2 - 3x^3 + , + (-1)^n * 3x^n, the sigma notation would be:
Σ[(-1)^k * 3x^k] from k=0 to n
Here's a step-by-step explanation:
1. Identify the pattern in the sum: It alternates between positive and negative terms, and each term has a power of x multiplied by 3.
2. Assign the variable k for the index of summation.
3. Determine the range of k: The sum starts with k=0 and goes up to k=n.
4. Represent the alternating sign using (-1)^k.
5. Combine all components to form the sigma notation: Σ[(-1)^k * 3x^k] from k=0 to n.
The sum can be written in sigma notation as:
\($\displaystyle\sum_{n=1}^\infty (-1)^n 3x^n$\)
How to write sum in sigma notation?The given series is:
\(3 - 3x + 3x^2 - 3x^3 + ...\)
To write it in sigma notation, we first notice that the terms alternate in sign, and each term is a power of x multiplied by a constant (-3). We can write the general term of the series as:
\((-1)^n * 3 * x^n\)
where n is the index of the term, starting from n = 0 for the first term.
Using sigma notation, we can express the sum of the series as:
\($\displaystyle\sum_{n=1}^\infty (-1)^n 3x^n$\)
where the summation is over all values of n starting from n = 0.
Learn more about sigma notation
brainly.com/question/27737241
#SPJ11
A spherical balloon is inflated so that its volume is increasing at the rate of 12 cubicfeet per minute. How fast is the radius of the balloon increasing when the radius is 6feet?
Answers
Given:
The rate of change in volume = 12 cubic feet per minute.
We need to find the rate of change of radius at radius = 6 feet.
Consider the formula to find the volume of the sphere.
\(V=\frac{4}{3}\pi r^3\)Differentiate with respect to t.
\(\frac{dV}{dt}=\frac{4}{3}\pi\times3r^2\times\frac{dr}{dt}\)\(\text{ Substitute }\frac{dV}{dt}=12\text{ and r=6 in the formula.}\)\(12=\frac{4}{3}\pi\times3(6)^2\times\frac{dr}{dt}\)\(12=144\pi\times\frac{dr}{dt}\)Dividing both sides by 144pi, we get
\(\frac{12}{144\pi}=\frac{dr}{dt}\)\(\frac{dr}{dt}=\frac{1}{12\pi}\)\(\frac{dr}{dt}=\frac{1}{37.68}=0.0265\text{ feet per minute}\)Hence the radius of the balloon increases by 0.03 feet per minute.
is (, ) = 3 − 32 an harmonic function? if yes, then find a corresponding analytic function ()
Answers
No, f(x, y) = 3x - 3y^2 is not a harmonic function.
A harmonic function is a twice continuously differentiable function f(x, y) that satisfies the Laplace equation:
∂²f/∂x² + ∂²f/∂y² = 0.
Let's check if f(x, y) = 3x - 3y^2 satisfies the Laplace equation:
∂²f/∂x² = ∂/∂x(3) = 0
∂²f/∂y² = ∂/∂y(-6y) = -6
∂²f/∂x² + ∂²f/∂y² = 0 + (-6) = -6 ≠ 0
Since the Laplace equation is not satisfied, f(x, y) = 3x - 3y^2 is not a harmonic function.
As for finding a corresponding analytic function, an analytic function is a function that is locally given by a convergent power series. Since f(x, y) is not a harmonic function, there is no corresponding analytic function.
Read more about harmonic functions at:
https://brainly.com/question/30385079
#SPJ11
The sun is at a focus of Earth's elliptical orbit.
a. Find the distance from the sun to the other focus.
Answers
The distance from the sun to the other focus is 5.01 × 10⁹ m.
What is the distance from the sun?
(a) The distance from the center of an ellipse to a focus is an where a is the semi major axis and e is the eccentricity. Thus, the separation of the foci ( in the case of Earth's orbit ) is;
2ae = 2(1.50 × 10¹¹)(0.0167) = 5.01 × 10⁹ m.
(b) To express this in terms of solar radii, we set up a ratio;
(5.01 × 10⁹)/(6.96 × 10⁸) = 7.2
Thus, we can conclude that the distance from the sun to the other focus is 5.01 × 10⁹ m.
Read more about Distance from Sun at; https://brainly.com/question/11494894
#SPJ1
Complete question is;
The Sun's center is at one focus of Earth's orbit. How far from this focus is the other focus, (a) in meters and (b) in terms of the solar radius, 6.96 × 10⁸ m? The eccentricity is 0.0167, and the semimajor axis is 1.50 × 10¹¹ m.
Consider a 1-D harmonic oscillator and a trial wavefunction of the form ψ(x)=A/(x^2 + α^(2)), [20] where A is the normalization constant and α is an adjustable parameter. (a) Determine A. [3] (b) Estimate the ground-state energy of the harmonic oscillator. [12] (c) Check whether ⟨H⟩ overestimates or underestimates the solution you obtained in 3(b), and hence describe the validity of the variational principle in this case. [5]
Answers
a.we get, `A = √(2α³/π)`.
b.`⟨H⟩ = (3/4)hω - (h²/4ma²)` where `a = α/√(mω/h)`.
c.we can say that the variational principle is valid in this case.
(a) Let's find the normalization constant A.
We know that the integral over all space of the absolute square of the wave function is equal to 1, which is the requirement for normalization. `∫⟨ψ|ψ⟩dx= 1`
Hence, using the given trial wavefunction, we get, `∫⟨ψ|ψ⟩dx = ∫ |A/(x^2+α²)|²dx= A² ∫ dx / (x²+α²)²`
Using a substitution `x = α tan θ`, we get, `dx = α sec² θ dθ`
Substituting these in the above integral, we get, `A² ∫ dθ/α² sec^4 θ = A²/(α³) ∫ cos^4 θ dθ`
Using the identity, `cos² θ = (1 + cos2θ)/2`twice, we can write,
`A²/(α³) ∫ (1 + cos2θ)²/16 d(2θ) = A²/(α³) [θ/8 + sin 2θ/32 + (1/4)sin4θ/16]`
We need to evaluate this between `0` and `π/2`. Hence, `θ = 0` and `θ = π/2` limits.
Using these limits, we get,`⟨ψ|ψ⟩ = A²/(α³) [π/16 + (1/8)] = 1`
Therefore, we get, `A = √(2α³/π)`.
Hence, we can now write the wavefunction as `ψ(x) = √(2α³/π)/(x²+α²)`.
(b) Using the wave function found in part (a), we can now determine the expectation value of energy using the time-independent Schrödinger equation, `Hψ = Eψ`. We can write, `H = (p²/2m) + (1/2)mω²x²`.
The first term represents the kinetic energy of the particle and the second term represents the potential energy.
We can write the first term in terms of the momentum operator `p`.We know that `p = -ih(∂/∂x)`Hence, we get, `p² = -h²(∂²/∂x²)`Using this, we can now write, `H = -(h²/2m) (∂²/∂x²) + (1/2)mω²x²`
The expectation value of energy can be obtained by taking the integral, `⟨H⟩ = ⟨ψ|H|ψ⟩ = ∫ψ* H ψ dx`Plugging in the expressions for `H` and `ψ`, we get, `⟨H⟩ = - (h²/2m) ∫ψ*(∂²/∂x²)ψ dx + (1/2)mω² ∫ ψ* x² ψ dx`Evaluating these two integrals, we get, `⟨H⟩ = (3/4)hω - (h²/4ma²)` where `a = α/√(mω/h)`.
(c) Since we have an approximate ground state wavefunction, we can expect that the expectation value of energy ⟨H⟩ should be greater than the true ground state energy.
Hence, the value obtained in part (b) should be greater than the true ground state energy obtained by solving the Schrödinger equation exactly.
Therefore, we can say that the variational principle is valid in this case.
To know more about time-independent Schrödinger equation,visit:
https://brainly.com/question/31642338
#SPJ11
I need help with number 11 and number 12

Answers
Answer:
11) 6
12) 3
Step-by-step explanation:
2 log 2 8
so 2(log2 8)
Base 2 so 2^x=8 so 3.
2*3 is 6.
log a a cubed
base a so a^ x = a^3
x=3
so 3.
Hope this helps ;D
Answer:
6 and 3
Step-by-step explanation:
Using the rules of logarithms
log\(x^{n}\) ⇔ n log x
\(log_{b}\) x = n ⇒ x = \(b^{n}\)
\(log_{a}\) a = 1
(11)
let 2 \(log_{2}\)8 = n , then
\(log_{2}\) 8² = n
\(log_{2}\) 64 = n
\(log_{2}\) \(2^{6}\) = n
\(2^{6}\) = \(2^{n}\)
Since bases on both sides are equal, equate the exponents, that is
n = 6
(12)
\(log_{a}\) a³
= 3 \(log_{a}\) a
= 3 × 1
= 3
a high school principal is deciding which electives will be offered to all students during the next school year. she plans to survey using a systematic sample. which of the following describes a systematic sample
Answers
A systematic sample is a sampling method in which members from a population are selected in a regular and systematic way.
What is systematic sample? Systematic sampling is a probability sampling technique in which sample members from a larger population are selected according to a random starting point but with a fixed, periodic interval. In other words, the population is divided into subgroups of equal size and a randomly selected member of each subgroup is chosen. Systematic sampling is useful when a larger sample is needed, and when it is difficult to select members from the population. It is also beneficial because it reduces the possibility of sample bias and increases the accuracy of the results. Additionally, it is relatively easy to implement, which makes it a popular sampling technique for researchers. However, systematic sampling has some drawbacks. Since the population is divided into equal subgroups, the sample size could be unbalanced. Thus, it is important to ensure that the subgroups are of equal size. Additionally, the periodic interval used to select sample members should be carefully chosen in order to avoid bias. Overall, systematic sampling is a practical and effective way to select a representative sample from a larger population. It can be used when a larger sample size is needed and when it is difficult to select members from the population in a random manner. However, it is important to ensure that the subgroups are of equal size and that the periodic interval used is chosen carefully in order to avoid bias.To learn more about systematic sample refer to:
https://brainly.com/question/28505229
#SPJ1
Pls Help!! Will mark Brainliest!!
Hopefully it will show the pic this time

Answers
Answer:
Question 7: Company A has a lower rate
Question 8: Caiden's vehicle gets more miles per gallon
Step-by-step explanation:
Question 7:
According to the table for Company B's rates, if you divide the total cost by the square footage in each row, you would get $2.75/ft² each time. Therefore, Company A would charge the Smiths a lower cost per square foot.
$2.25/ft² < $2.75/ft²
Company A < Company B
Question 8:
Using the given equation, we already know that Caiden's vehicle has a gas mileage of 16.2 miles/gallon The graph for Ethan's gas mileage can be figured out using slope. Taking the points (0, 0) and (2, 30) on the line, we can figure out the line's slope.
slope = rise/run,
where "rise" is how much you add or subtract to get from the first y-value to the second, and "run" is how much you add or subtract to get from the first x-value to the second.
slope = rise/run
slope = 30/2
slope = 15/1
The slope of the line is 15, so that means the line's equation is y = 15x. Therefore, Ethan's gas mileage is 15 miles/gallon.
16.2 mpg > 15 mpg
Caiden > Ethan
Find the area of the following
parallelogram:
3 cm
5 cm
4.5 cm
A= [?] cm
Enter the exact answer as a decimal.
![Find the area of the followingparallelogram:3 cm5 cm4.5 cmA= [?] cmEnter the exact answer as a decimal.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/TYJtjnpLxyCBehbJvJC5tsaaxNvmMMlw.png)
Answers
Answer:
The answer is 13.5
Step-by-step explanation:
After the first term, a, in a sequence the ratio of each term to the preceding term is r:1. What is the third term in the sequence?
Answers
The third word in the series is an a x r², and this is the answer to the given question based on the sequence.
What is Sequence?A progression in mathematics is a particular form of sequence where the distance between succeeding terms is constant. A collection of numbers or other mathematical elements arranged in a specific order is called a sequence.
Arithmetic progressions, geometric progressions, and harmonic progressions are only a few of the several forms of progressions. The formula for the nth term of the sequence varies depending on the type of progression.
By dividing the first term by the common ratio r, one may get the second term in the sequence:
Second term = a x r
The second term can also be multiplied by the common ratio r to find the third term:
Third term = (a x r) x r = a x r²
As a result, an a x r² is the third term in the series.
To know more about geometric progressions, visit:
https://brainly.com/question/24643676
#SPJ1
The lengths of the sides of a quadrilateral are 4 consecutive even integers. The perimeter of the quadrilateral is 36 inches. What is the length of the longest side?\
WILL GIVE BRAINLIEST
NEED THIS ASAP
Answers
Answer:
The length of the longest side is 9 inches
Step-by-step explanation:
The given parameters for the quadrilateral is that the length of the sides are;
The length of the sides are consecutive integers = x, x + 2, x + 4, x + 6
The perimeter of the rectangle = 36 inches
The side length to be found = The length of the longest side = x + 3
2 6 10 14 18
∴ x + x + 2 + x + 4 + x + 6 = 36
4·x + 12 = 36
4·x = 36 - 12 = 24
4·x = 24
x = 24/4 = 6
x = 6 inches
The length of the longest side = x + 3 = 6 + 3 = 9
The length of the longest side = 9 inches.
Answer:
The length of the longest side is 9 inches
Step-by-step explanation:
The given parameters for the quadrilateral is that the length of the sides are;
The length of the sides are consecutive integers = x, x + 2, x + 4, x + 6
The perimeter of the rectangle = 36 inches
The side length to be found = The length of the longest side = x + 3
2 6 10 14 18
∴ x + x + 2 + x + 4 + x + 6 = 36
4·x + 12 = 36
4·x = 36 - 12 = 24
4·x = 24
x = 24/4 = 6
x = 6 inches
The length of the longest side = x + 3 = 6 + 3 = 9
The length of the longest side = 9 inches.
credit to oeerivona https://brainly.com/app/profile/18148767
What is the exact value of sine of 8 pie/3
Answers
Answer:
0.1456858
Step-by-step explanation:
Hope it help
Answer:
−1/2
Explanation:
cos(8π/3)
=cos(8π/3 − 2π)
=cos(2π/3) = − cos (π/3) = −1/2
Select the correct formula to solve for x.
cos (33) = x/14
sin (33) = x/14
cos (33) = 14/x
sin (33) = 14/x

Answers
Answer: Choice B) sin (33) = x/14
This is because the sine of an angle is equal to the opposite side over the hypotenuse
sin(angle) = opposite/hypotenuse
sin(33) = x/14
We can't use cosine because we don't have a variable for the adjacent side.
Solve for x. Figures are not necessarily drawn to scale.

Answers
Check the picture below.
\(\cfrac{17.5+14}{17.5}~~ = ~~\cfrac{x}{12.5}\implies \cfrac{(17.5+14)(12.5)}{17.5}~~ = ~~x\implies 22.5=x\)

Problem of Tartaglia (1500-1577): among all positive numbers a, b whose sum is 8, find those for which the product of the two numbers and their difference is largest. (Enter your answers as a comma-separated list.)
a, b = _____
Let x = a - b and express abx in terms of x alone.
Answers
As per the information provided, a = 4√3/3 + 4, b = 4 - 4√3/3 the answer can be calculated with optimization method. it will be as follows:
Sum of a and b is 8, we get
a+b=8
b=8−a
Now, let x=a−b
Then we get,
\(x=a−(8−a) \\ x=2a−8 \\ x+8=2 \\ 1 \div 2x+4=a
\)
we use this to answer to solve for b
\(b=8−a \\ =8−(1 \div 2x+4) \\ =4−1 \div 2x
\)
Now we use the product of two numbers and its difference. This can be expressed as:
\(a⋅b⋅x=(1 \div 2x+4)(4−1 \div 2x) \\ x=2 {x}^{2} − \frac{1}{4} {x}^{3} +16x−2x^{2} \\ =−14x^{3} +16x
\)
Thus, this expression that we need to maximize. Take the derivative, set it equal to zero, and solve for x
\(−3 \div 4x ^{2} +16=0 \\ 16 =3 \div 4 x ^{2} \\ 643=x \\ 28√3 \div 3=x\)
Now for us to check that this is a maximum, we have to note that the second derivative is
\(−3 \div 2x
\\ At \\
x=8√3 \div 3
\)
the second derivative is −4√3. Since this number is negative, the point is a maximum.
Now we must find the values of a and b for this x. We have to use the relationship
\(a=1 \div 2x+4\)
\(a=1 \div 2 \times 8√3 \div 3+4 \\ =4√3 \div 3+4\)
now we use the relationship b=8−a
\(b=8−(4√3 \div 3+4) \\ =4−4√3 \div 3\)
The first step in determining a function's maximum or minimum value is differentiating it. Then, set this derivative to zero and conduct the computation.
x. This will reveal the location of a function's maximum or minimum, but it won't reveal which.
Take the second derivative to get more details. A local maximum occurs when both the first and second derivatives are negative. You have a local minimum when both the first derivative and the second derivative are zero.
To learn more about optimization: https://brainly.com/question/28970005
#SPJ4
Find the value of the indicated trigonometry ratio cos in right tringle with side of 6,6*squort 2, 6*squort 3
Answers
Answer:√2/2
Step-by-step explanation:
Let's label the sides of the right triangle as follows:
The side adjacent to the angle θ (cosine is adjacent/hypotenuse): 6
The hypotenuse (the longest side): 6√2
The side opposite to the angle θ (sine is opposite/hypotenuse): 6√3
Using the Pythagorean theorem, we can find the length of the missing side:
a² + b² = c²
6² + (6√3)² = (6√2)²
36 + 108 = 72
144 = 72
√144 = √72
12 = 6√2
Now that we know the length of all three sides, we can use the cosine ratio to find the value of cos(θ):
cos(θ) = adjacent/hypotenuse = 6/6√2 = √2/2
Therefore, the value of cos(θ) in the right triangle with sides of 6, 6√2, and 6√3 is √2/2.