What number gives a result of −1 when 9 is subtracted from the quotient of the number and 4?
Answers
Step-by-step explanation:
x/4 - 9 = -1
×/4 = -1 + 9
x/4 = 8
4 (x/4) = 4 (8)
x = 32
Answer:
32
Step-by-step explanation:
(Quotient of a and b = a/b)
Let the number = x
Quotient of the number and four: x/4
9 subtracted from the quotient of the number and four: x/4 - 9
-1 is the result of 9 subtracted from the quotient of the number and four: x/4 - 9 = -1
x/4 -9 = -1
x/4 = 8
x = 32
Related Questions
A person standing on the ground outside a building throws a set of keys directly upward to a person standing on a second-floor balcony. The person on the ground releases the keys with an initial vertical velocity of 28 ft/s from a height of 4 ft. The function h(t) = 16t^2 + 28t +4 models the height (in feet) of the keys at time t (in seconds) after the keys are thrown. The person standing on the balcony can catch the keys once they reach a height of 12 ft. For what period of time are the keys high enough to be caught?
a [0,1.88]
b[0.36,1.39]
c[0,0.36] U [1.39,1.88]
d(-∞,0.36] U [1.39,∞)
Answers
Answer:
Step-by-step explanation:
Choose the equation of the line in standard form and slope-intercept form from the graph given.
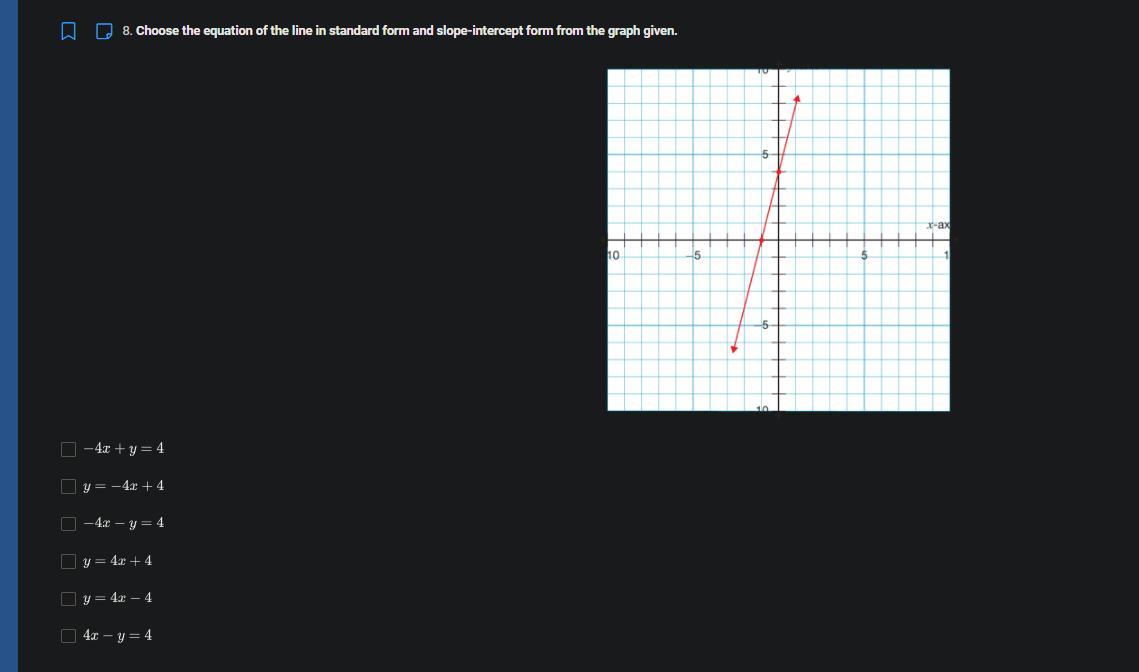
Answers
Answer:
standard form: -4x + y = 4
slop-intercept form: y = 4x + 4
Step-by-step explanation:
Find two points on the line: (0, 4) and (-1, 0)
slope = change in y ÷ change in x = (4 - 0) ÷ (0 - -1) = 4 ÷ 1 = 4
from inspection, y-intercept = 4
Therefore, equation of line in slope-intercept form: y = 4x + 4
Now use this to determine standard form
Standard form: Ax+By=C
so for y = 4x + 4
standard form is: -4x + y = 4
Which is the better buy: 12 OZ for $1.25or 18 OZ for $1.75?
Answers
Answer:
18 OZ is better$1.75 to buy
what is the equation of the line in slop-intercept form HELPP PLZZZZZZZZZZ

Answers
Answer:
y = 3/5x + 3
Step-by-step explanation:
(y2-y1)/(x2-x1) = slope
pick 2 points (0,3) and (-5,0)
(0-3)/(-5-0) = -3/-5 = 3/5
y = 3/5x + b
3 = 3/5(0) + b, b = 3
equation y = 3/5x + 3
how oes the relationship between logarithms and exponential functions help us find solutions

Answers
The relationship between logarithms and exponential functions is fundamental and provides a powerful tool for finding solutions in various mathematical and scientific contexts.
Logarithms are the inverse functions of exponential functions. They allow us to solve equations and manipulate exponential expressions in a more manageable way. By taking the logarithm of both sides of an exponential equation, we can convert it into a linear equation, which is often easier to solve.
One of the key properties of logarithms is the ability to condense multiplication and division operations into addition and subtraction operations. For example, the logarithm of a product is equal to the sum of the logarithms, and the logarithm of a quotient is equal to the difference of the logarithms.
Logarithms also help us solve equations involving exponential growth or decay. By taking the logarithm of both sides of an exponential growth or decay equation, we can isolate the exponent and solve for the unknown variable.
This is particularly useful in fields such as finance, population modeling, and radioactive decay, where exponential functions are commonly used.
Furthermore, logarithms provide a way to express very large or very small numbers in a more manageable form. The logarithmic scale allows us to compress a wide range of values into a smaller range, making it easier to analyze and compare data.
In summary, the relationship between logarithms and exponential functions enables us to simplify and solve equations involving exponential expressions, model exponential growth or decay, and manipulate large or small numbers more effectively.
For more such question on logarithms visit:
https://brainly.com/question/25993029
#SPJ8
The point (-2, -5) is on the line given by which equation below?
A. y=2x
B. y=-3x
C. y=x+3
D. y=x-3
Answers
Answer:
D
Step-by-step explanation:
Substitute x = - 2 into the right side of each equation and if the result is y = - 5 then the point is on that equation.
A
y = 2x = 2(- 2) = - 4 ≠ - 5
B
y = - 3x = - 3(- 2) = 6 ≠ - 5
C
y = x + 3 = - 2 + 3 = 1 ≠ - 5
D
y = x - 3 = - 2 - 3 = -5 ← (- 2, 5) is on this equation → D
Need to find OM and NM given AO= 6371 angle NOE= 16.26 deg and that AO bisects angle NOEIf it helps at all the point O is in the center of the circle and segment OA is the radius

Answers
As you can see the segments OM ME and OE form a right triangle. So to find the measure of the segment OM you can use the trigonometric ratio cos (θ):
\(\cos (\theta)=\frac{\text{ Adjacent side}}{\text{ Hypotenuse}}\)So, you have:
\(\begin{gathered} \cos (MOE\text{)}=\frac{OM}{OE} \\ \cos (8.13\text{\degree)}=\frac{OM}{6371} \end{gathered}\)Angle MOE measures 8.13 ° because segment AO bisects angle NOE.
\(\frac{16.26\text{\degree}}{2}=8.13\text{\degree}\)The measure of segment OE is 6371 because it is a radius of the circle just like segment AO.
\(\begin{gathered} \cos (8.13\text{\degree)}=\frac{OM}{6371} \\ \text{ Multiply by 6371 on both sides of the equation } \\ \cos (8.13\text{\degree)}\cdot6371=\frac{OM}{6371}\cdot6371 \\ \cos (8.13\text{\degree)}\cdot6371=OM \\ 6306.97=OM \end{gathered}\)Now, to find the measure of segment NM you can use the trigonometric ratio sin (θ):
\(\sin (\theta)=\frac{\text{Opposite side}}{\text{ Hypotenuse}}\)Also, the NM and ME segments are equal because the AO segment bisects the NOE angle. So, you have:
\(NM=ME\)\(\begin{gathered} \sin (MOE)=\frac{ME}{OE} \\ \sin (8.13\text{\degree})=\frac{ME}{6371} \\ \text{ Multiply by 6371 on both sides of the equation} \\ \sin (8.13\text{\degree})\cdot6371=\frac{ME}{6371}\cdot6371 \\ \sin (8.13\text{\degree})\cdot6371=ME \\ 900.98=ME \\ \text{ Then} \\ 900.98=NM \end{gathered}\)Therefore, the measurements of the OM and NM segments are:
\(\begin{gathered} 6306.97=OM \\ 900.98=NM \end{gathered}\)

Find the exact value of each of the remaining trigonometric functions of θ. Rationalize denominators when applicable.
secθ=−8, given that sinθ>0
Answers
The exact values of the remaining trigonometric functions of θ are:
sin(θ) = √(1/64)
cos(θ) = -8
tan(θ) = -8√(1/64)
csc(θ) = 1
cot(θ) = -√(1/64) / 8
Given that sec(θ) = -8 and sin(θ) > 0, we can find the exact values of the remaining trigonometric functions using the Pythagorean identity:
sec^2(θ) = 1/sin^2(θ)
Substituting the value of sec(θ), we have:
(-8)^2 = 1/sin^2(θ)
64 = 1/sin^2(θ)
sin^2(θ) = 1/64
sin(θ) = ±√(1/64)
Since sin(θ) > 0, we take the positive square root:
sin(θ) = √(1/64)
Next, we use the reciprocal identity for cosecant:
csc(θ) = 1/sin(θ)
Substituting the value of sin(θ), we have:
csc(θ) = 1/√(1/64) = 8√(1/64) = 8/√(64) = 8/8 = 1
Next, we use the reciprocal identity for cotangent:
cot(θ) = 1/tan(θ)
We can find the value of tan(θ) using the definition:
tan(θ) = sin(θ) / cos(θ)
Substituting the values of sin(θ) and cos(θ), we have:
tan(θ) = √(1/64) / (-8) = -√(1/64) / 8
Finally, we use the reciprocal identity for a tangent:
tan(θ) = 1/cot(θ)
Substituting the value of cot(θ), we have:
tan(θ) = -8√(1/64)
Therefore, the exact values of the remaining trigonometric functions of θ are:
sin(θ) = √(1/64)
cos(θ) = -8
tan(θ) = -8√(1/64)
csc(θ) = 1
cot(θ) = -√(1/64) / 8
The complete question is:-
Find the exact value of each of the remaining trigonometric functions of
θ. Rationalize denominators when applicable.
secθ=−8, given that sinθ>0
To learn more about trigonometric functions, refer:-
https://brainly.com/question/6904750
#SPJ4
How many quarts are equal to 17 gallons?
Answers
Answer:
it should be 68 US quarts
Carlos read 150 words in one minute. He
read 5 times as many words as his younger
brother. How many words did his younger brother
read in one minute?
Answers
Answer:
30
Step-by-step explanation:
150/5 = 30
Answer: 30
Step-by-step explanation:
Please help I am so lost thank you all

Answers
h = hours till they're 58 miles apart
Check the picture below.
so they're travelling in opposite directions, however the combined distances is 58 miles at say "h" hours, by the time that happend Hopi has been walking "h" hours and Brittany has also being walking "h" hours too.
Since the combined distance is 58 miles than if Hopi has covered "m" miles then Brittany covered the slack of "58 - m".
\({\Large \begin{array}{llll} \underset{distance}{d}=\underset{rate}{r} \stackrel{time}{t} \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lcccl} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ Hopi&m&15&h\\ Brittany&58-m&14&h \end{array}\hspace{5em} \begin{cases} m=(15)(h)\\\\ 58-m=(14)(h) \end{cases} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{substituting on the 2nd equation}}{58-(\stackrel{m}{15h})=14h}\implies 58=29h\implies \cfrac{58}{29}=h\implies \boxed{2=h}\)

I want you to find the answer

Answers
The value of length BC is 18.9
What is cosine rule?Cosine Rule states that the square of the length of any side of a given triangle is equal to the sum of the squares of the length of the other sides minus twice the product of the other two sides multiplied by the cosine of angle included between them.
Therefore,
c² = a² + b² - 2abcosC
To find the length BC we use cosine rule.
c² = 13² + 7² - 2(13)(7)cos140
c² = 218 - 182cos140
c² = 218-(-139.42)
c² = 218+139.2
c² = 357.2
c = √357.2
c = 18.9
Therefore, the length of BC is 18.9
learn more about cosine rule from
https://brainly.com/question/23720007
#SPJ1
In the triangle, the value of the side BC is 18.9cm to 1 decimal place
How to determine BC?The side BC can be found using the cosine formula, Remember that Cosine Rule states that the square of the length of any side of a given triangle is equal to the sum of the squares of the length of the other sides minus twice the product of the other two sides multiplied by the cosine of angle included between them.
The cosine formula states that
c² = a² + b² - 2abcosC
To find the length BC we use cosine rule.
c² = 13² + 7² - 2(13)(7)cos140
c² = 218 - 182cos140
c² = 218-(-139.42)
c² = 218+139.2
c² = 357.2
c = √357.2
c = 18.9
In conclusion, the value of the length of BC is 18.9cm
Learn more about the cosine rule on https://brainly.com/question/28716982?
#SPJ1
Rita rolled a die 25 times. Her results are shown in the table below:
Please help me with this, Please get answer from the table and not by the internet. Thank you! :)

Answers
Answer:
Here I see your answer
Step-by-step explanation:

Apply the formula d=r⋅t to answer the following questions.
Part A
Tom drove a total of 150 miles in 3 hours. Assuming he drove at a constant speed, what speed was Tom driving?
______ miles per hour
Question 2
Part B
Zac drove for 2.5 hours at a constant speed of 40 miles per hour. How many miles did he drive?
______ miles
Question 3
Part C
Dan drove 130 miles at a constant speed of 65 miles per hour. How many hours did he drive?
_____ hours
Answers
Using the formula d = rt we have: Part A: Tom was driving at a speed of 50 miles per hour. Part B: Zac drove 100 miles. Part C: Dan drove for 2 hours.
What is distance formula?The link between distance, rate, and time is demonstrated by the equation d = r*t. The product of the rate (r) and the time (t) yields the distance (d) (t). In other words, the velocity of motion and the amount of time spent travelling affect the distance covered. Assuming that the time spent travelling is constant, increasing the rate of movement will result in an increase in the amount of distance travelled in a given amount of time. According to this, as journey duration increases, so does the distance travelled.
The given formula is d = r(t).
Part A:
Tom drove a total of 150 miles in 3 hours, so:
150 miles = r * 3 hours
r = 50 miles per hour
Part B:
constant speed of 40 miles per hour for 2.5 hours, so:
d = 40 miles per hour * 2.5 hours
d = 100 miles
Part C:
constant speed of 40 miles per hour for 2.5 hours, so:
130 miles = 65 miles per hour * t
t = 130 miles / 65 miles per hour
t = 2 hours
Learn more about distance here:
https://brainly.com/question/15172156
#SPJ1
The tickets for the field trip were purchased yesterday for both students and instructors. Children tickets cost $9, adult tickets cost $11. The number of children tickets purchased was three more than ten times the number of adults tickets purchased. How many of each were purchased if all of the tickets cost a total of $936 dollars?
Answers
The 9 adult tickets and 93 children tickets were purchased.Let's assume the number of adult tickets purchased is "a" and the number of children tickets purchased is "c."
According to the given information, children tickets cost $9 and adult tickets cost $11. So, the total cost of children tickets is 9c, and the total cost of adult tickets is 11a.
The problem also states that the total cost of all the tickets is $936. Therefore, we can write the following equation:
9c + 11a = 936
Additionally, it is mentioned that the number of children tickets purchased was three more than ten times the number of adult tickets purchased:
c = 10a + 3
We can now solve this system of equations to find the values of "a" and "c." By substituting the value of "c" from the second equation into the first equation, we have:
9(10a + 3) + 11a = 936
90a + 27 + 11a = 936
101a = 936 - 27
101a = 909
a = 909 / 101
a = 9
Substituting this value back into the second equation, we find:
c = 10(9) + 3
c = 90 + 3
c = 93.
For more such questions on Purchased:
https://brainly.com/question/28717901
#SPJ8
Imagine a clock with the hour hand at 12 and the minute hand at 2. Does the angle formed by the two hands have a measure greater than, less than, or equal to 1/4 turn?
Answers
The angle formed by the two hands have a measure less than 1/4 turn
How to relate the measure of the angle to 1/4 turn?From the question, we have the following parameters that can be used in our computation:
A clock with the hour hand at 12 and the minute hand at 2
The turn represented by the above is represened as
Turn = (2 * 30)/360
When simplified, we have
Turn = 1/6
Next, we have
Angle at the turn = 1/4
1/6 is less than 1/4
This means that the angle formed by the two hands have a measure less than 1/4 turn
Read more about angles at
https://brainly.com/question/25716982
#SPJ1
If b = -2, what is 3b-7 ?
Answers
3 x -2 = -6
-6 -7 = -13
In the following problem, check that it is appropriate to use the normal approximation to the binomial. Then use the normal distribution to estimate the requested probabilities. It is estimated that 3.7% of the general population will live past their 90th birthday. In a graduating class of 723 high school seniors, find the following probabilities. (Round your answers to four decimal places.)
(a) 15 or more will live beyond their 90th birthday
0.9846 x
(b) 30 or more will live beyond their 90th birthday
.2119
(c) between 25 and 35 will live beyond their 90th birthday
(d) more than 40 will live beyond their 90th birthday
Answers
Answer:
a) 0.9920 = 99.20% probability that 15 or more will live beyond their 90th birthday
b) 0.2946 = 29.46% probability that 30 or more will live beyond their 90th birthday
c) 0.6273 = 62.73% probability that between 25 and 35 will live beyond their 90th birthday
d) 0.0034 = 0.34% probability that more than 40 will live beyond their 90th birthday
Step-by-step explanation:
We solve this question using the normal approximation to the binomial distribution.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
\(E(X) = np\)
The standard deviation of the binomial distribution is:
\(\sqrt{V(X)} = \sqrt{np(1-p)}\)
Normal probability distribution
Problems of normally distributed distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that \(\mu = E(X)\), \(\sigma = \sqrt{V(X)}\).
In this problem, we have that:
Sample of 723, 3.7% will live past their 90th birthday.
This means that \(n = 723, p = 0.037\).
So for the approximation, we will have:
\(\mu = E(X) = np = 723*0.037 = 26.751\)
\(\sigma = \sqrt{V(X)} = \sqrt{np(1-p)} = \sqrt{723*0.037*0.963} = 5.08\)
(a) 15 or more will live beyond their 90th birthday
This is, using continuity correction, \(P(X \geq 15 - 0.5) = P(X \geq 14.5)\), which is 1 subtracted by the pvalue of Z when X = 14.5. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{14.5 - 26.751}{5.08}\)
\(Z = -2.41\)
\(Z = -2.41\) has a pvalue of 0.0080
1 - 0.0080 = 0.9920
0.9920 = 99.20% probability that 15 or more will live beyond their 90th birthday
(b) 30 or more will live beyond their 90th birthday
This is, using continuity correction, \(P(X \geq 30 - 0.5) = P(X \geq 29.5)\), which is 1 subtracted by the pvalue of Z when X = 29.5. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{29.5 - 26.751}{5.08}\)
\(Z = 0.54\)
\(Z = 0.54\) has a pvalue of 0.7054
1 - 0.7054 = 0.2946
0.2946 = 29.46% probability that 30 or more will live beyond their 90th birthday
(c) between 25 and 35 will live beyond their 90th birthday
This is, using continuity correction, \(P(25 - 0.5 \leq X \leq 35 + 0.5) = P(X 24.5 \leq X \leq 35.5)\), which is the pvalue of Z when X = 35.5 subtracted by the pvalue of Z when X = 24.5. So
X = 35.5
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{35.5 - 26.751}{5.08}\)
\(Z = 1.72\)
\(Z = 1.72\) has a pvalue of 0.9573
X = 24.5
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{24.5 - 26.751}{5.08}\)
\(Z = -0.44\)
\(Z = -0.44\) has a pvalue of 0.3300
0.9573 - 0.3300 = 0.6273
0.6273 = 62.73% probability that between 25 and 35 will live beyond their 90th birthday.
(d) more than 40 will live beyond their 90th birthday
This is, using continuity correction, P(X > 40+0.5) = P(X > 40.5), which is 1 subtracted by the pvalue of Z when X = 40.5. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{40.5 - 26.751}{5.08}\)
\(Z = 2.71\)
\(Z = 2.71\) has a pvalue of 0.9966
1 - 0.9966 = 0.0034
0.0034 = 0.34% probability that more than 40 will live beyond their 90th birthday
A pollster estimated that Greg Wilder would receive 3,600 votes for a seat on the school board. The actual number of votes Wilder received was 3,750. What was the percent error in the pollster's prediction?
A. 4%
B. 6%
C. 15%
D. 42%
Answers
Use the circle below to solve for each questions.

Answers
Answer:
its area us 153.94
its diameter is 14cm
its radius is 7cm
its circumference is 43.98
Step-by-step explanation:
area of circle means πr square
diameter means 2r
radius already given
circumference means. 2πr
If the area of a square inscribed in a circle is
25, what is the area of the circle?
Answers
The area of a square inscribed in a circle is 25, then the area of the circle is 25π/2 or approximately 39.27 square units.
To solve this problem, we can use the relationship between the area of a square inscribed in a circle and the area of the circle itself.
When a square is inscribed in a circle, the diagonal of the square is equal to the diameter of the circle. Let's assume that the side length of the square is 's' and the radius of the circle is 'r'.
We are given that the area of the square is 25, so we can find the side length of the square:
Area of square = \(s^2 = 25\)
Taking the square root of both sides, we get:
s = √25 = 5
Since the diagonal of the square is equal to the diameter of the circle, we can find the diameter of the circle:
Diagonal = Diameter = s√2 = 5√2
The radius of the circle is half the diameter, so:
Radius = 5√2 / 2 = (5√2)/2
Now, we can calculate the area of the circle using the formula:
Area of circle = \(\pi r^2\)
Substituting the value of the radius, we get:
Area of circle = π((5√2)/\(2)^2\) = π(25/2) = 25π/2
Therefore, the area of the circle is 25π/2 or approximately 39.27 square units.
For more question on square visit:
https://brainly.com/question/428672
#SPJ8
2/5 of employees in a company drive to work, 1/3 travel by bus and the rest walk. 1. Find the fraction of who walk.
Answers
Answer:
4/15
Step-by-step explanation:
2/5 drive
1/3 bus
and rest walk
fraction of those who walk is 1-(2/5+1/3)
2/5+1/3=(6+5)/15=11/15
15/15-11/15=4/15
You invested $6000 between two accounts paying 2% and 8% annual interest, respectively. If the total interest earned for the year was $360, how much was invested at each rate?
Answers
Based on the amount invested into the two accounts and their interest rates, the amount invested at each rate is:
8% - $4,0002% - $2,000How to find the amount invested at each rate?Assuming the amount invested at 2% is x, then the formula for this amount would be:
0.02x + 0.08 (6,000 - x ) = 360
Solving for x gives:
0.02x + 0.08 (6,000 - x ) = 360
2x + 48,000 - 8x = 36,000
6x = 12,000
x = 12,000 / 6
x = $2,000
The amount invested at 8% is:
= 6,000 - 2,000
= $4,000
Find out more on amounts invested at different rates at https://brainly.com/question/819035
#SPJ1
Pls help I’ll brainlest

Answers
Answer:
4
Step-by-step explanation:
the answer is
Multiply by 4
Dividing fractions word problem,
I need your help, yes you!

Answers
Answer: 2
Step-by-step explanation:
Answer:
I think it's 2kg
Step-by-step explanation:
13/5 ÷ 13/10
Reciprocate
13/5 × 10/13
= 26/13
=2kg
Factor out the greatest common factor

Answers
What is
5/6
as a decimal rounded to 3 decimal places
Answers
Answer:
its 0.833
Step-by-step explanation:
you do the numerator divided by the denomanater (im sorry i cant spell it haha)
so in this case 5 divided by 6 is 0.833
Anthe answer is 0.833
need help will give brainlist

Answers
Only set B: (-1,-3), (4,2), (6,4) appears to lie on the graph of a linear function, as the slopes between any two points remain constant.
To determine which set of points appears to lie on the graph of a linear function, we can check if the slope between any two points remains constant.
Let's calculate the slopes for each set of points:
A. (0,2), (3,1), (4,6)
The slope between (0,2) and (3,1):
m1 = (1 - 2) / (3 - 0) = -1/3
The slope between (3,1) and (4,6):
m2 = (6 - 1) / (4 - 3) = 5
We can see that the slopes are not equal, so this set of points does not lie on the graph of a linear function.
B. (-1,-3), (4,2), (6,4)
The slope between (-1,-3) and (4,2):
m1 = (2 - (-3)) / (4 - (-1)) = 5/5 = 1
The slope between (4,2) and (6,4):
m2 = (4 - 2) / (6 - 4) = 2/2 = 1
The slopes are equal, so this set of points appears to lie on the graph of a linear function.
C. (-3,-2), (0,0), (2,4)
The slope between (-3,-2) and (0,0):
m1 = (0 - (-2)) / (0 - (-3)) = 2/3
The slope between (0,0) and (2,4):
m2 = (4 - 0) / (2 - 0) = 4/2 = 2
The slopes are not equal, so this set of points does not lie on the graph of a linear function.
D. (5,-7), (0,-2), (2,2)
The slope between (5,-7) and (0,-2):
m1 = (-2 - (-7)) / (0 - 5) = 5/(-5) = -1
The slope between (0,-2) and (2,2):
m2 = (2 - (-2)) / (2 - 0) = 4/2 = 2
The slopes are not equal, so this set of points does not lie on the graph of a linear function.
Based on the calculations, only set B: (-1,-3), (4,2), (6,4) appears to lie on the graph of a linear function, as the slopes between any two points remain constant.
Learn more about slopes at:
https://brainly.com/question/3493733
#SPJ1
The sum of ages of two brothers is 38.Four years ago the age of the elder brother was the square of the younger brother.Find their ages.
Answers
Answer:
Older: 29 Younger:9
Step-by-step explanation:
First from 38, you subtract 8, 4 years for each brother and you get 30 years together. Then you find out that 25+5=30, and 5^2=25. Then you add 4 to each age to find their present day ages. Pls award brainliest for this
Guys please help me its really important i only have a bit of time

Answers
Answer:
B
A
Step-by-step explanation:
Use the graph to find the amplitude and period.
Notice amplitude is the absolute value of the number in front of either sin or cos
please give a heart for thanks :)

