What is the y intercept of the line 3y+8x-18=0?
Answers
Answer: y= 8/3x + 6
Step-by-step explanation:
Related Questions
decide whether parallelogram $jklm$ is a rectangle, a rhombus, or a square. give all names that apply.$j(-4,\ 2),\ k(0,\ 3),\ l(1,-1),\ m(-3,-2)$
Answers
The slopes of opposite sides are equal and product of slopes of adjacent sides is -1. All the sides are of equal length. So the given parallelogram is a square.
First we have to calculate the slopes of each sides.
Equation for slope, m= (y₂-y₁)/(x₂-x₁)
Slope of JK, m₁ = (3-2)/(0-⁻4) = 1/4
Slope of KL, m₂ = (-1-3)/(1-0) = -4
Slope of LM, m₃ = (-2-⁻1)/(-3-1) = 1/4
Slope of MJ, m₄ = (-2-2)/(-3--4)= -4
m₁= m₃ and m₂= m₄. That means the slope of opposite sides are equal. So they are parallel. Now we have to check whether the slopes are perpendicular.
If two lines are perpendicular, then product of slope will be -1
Multiplying two adjacent slopes,
m₁ ×m₂= 1/4 × -4 = -1
m₂ × m₃ = -4 × 1/4 = -1
m₃ m₄ = -4 × 1/4 = -1
So opposite sides are parallel and corresponding sides are perpendicular. So it may be a square or a rectangle.
Now we have to find the length of each sides,
Distance formula = \(\sqrt{{(x_{2}-x_{1})^{2} + (y_{2}-y_{1})^{2}\)
JK = \(\sqrt{(0--4)^{2}+ (3-2)^{2} }\) = √16+1 = √17
KL = √(1-0)²+(-1-3)² = √(1+16) = √17
LM = √(-3-1)²+(-2--1)² =√(16+1) =√17
MJ = √(-3--4)²+(-2-2)² =√1+16) =√17
Length of all sides are equal.
So the given parallelogram is a square.
For more information regarding slope and distance of coordinate points, kindly refer
https://brainly.com/question/29121002
#SPJ4
2+2=?
to those who wanna answer easy questions!
Answers
Answer:
4
Step-by-step explanation:
What you will need to do is add 4
the 2 to the other 2 which will get you 4
Answer:
4
Step-by-step explanation:
1+1 equal 2
2+2 equal 4
kkwiwoasnab. ajakhahakakaiahahhahaa
A rectangular swimming pool has length (x + 4) meters and width (x - 2) meters. The area of the
pool is 72 square meters. The length of the pool is ----- meters.
12
4.
8
16
Answers
Answer:
The length if the pool is 12
Step-by-step explanation:
Formula: A=lw or lw=A
> (x+4)(x-2)=72
> (x²-2x+4x-8)=72
> x²+2x-8=72
> x²+2x-8-72=0
> x²+2x-80=0
Factor
> x²+10x-8x-80
> x(x+10)-8(x+10)
>(x+10)(x-8)
Check:
(x-4); (x-2); x=8
(8+4)=12 Length
(8-2)=6 Width
What is the constant of proportionality in the equation y=5/4x
Answers
The constant of proportionality in the equation is 5/4
What is constant of proportionality?The constant connecting two given numbers in what is known in a proportional relationship is the constant of proportionality.
The constant of proportionality may also be referred to as the constant ratio, constant rate, unit rate, constant of variation, or even the rate of change.
In the problem, y = 5/4x
The constant term 5/4 as used in the equation is used t multiply the input x values to get the out put y values
The term helps in relating x to y
Learn more about constant of proportionality at:
https://brainly.com/question/27598477
#SPJ1
3. Figure ABCD Shown below is
made up of a semlore and a
rectangle. O is the contre of the
line DC
(Use
- )
10 cm
Calculate the area of
anglo AOB
Answers
Answer:
In a rectangle ABCD of 3 mx 4 m, starting from A and D, along the sides AB and DC after every 30 cm, a square shape of 10 cm is taken out as shown below. What will be the perimeter (in cm)
Step-by-step explanation:
12 CM And 300 CM is the answer
4. Kaya ran 1 2/5miles on Monday and 2 1/3 miles on
Tuesday. What was the total distance, in miles, Kaya
ran during those 2 days?
Answers
Answer: 3 11/15 please mark brainliest If I helped you.
the question is kayar and 12 by 5 miles on Monday and 21 by three miles on Tuesday what is the total distance in miles kayuren during those two days first phone on Monday how much run that was 12 by 5 miles on Tuesday Shirin to 1 by 3 minus now this whole part and fractional part are written separately so this can be converted into a mixed fraction like when a number is of the form of p by see that is one whole number and fraction then it is written as a + b by c so we can write Monday that was 12 by 5 miles that is
12 by 1 + 2 by 5 that will be 5 will be LCM of 5 + 2 will be 7 by 5 MI and Tuesday it will be 21 by 3 that is 2 + 1 by 3 3 will be the LCM of 3 and 22 will be 6 plus one that is 7 by 3 minus in question is asked that what was the total distance kayar and thus during today's so Monday plus Tuesday will be the total total 27 by 5 + 7 by 3 that will be equal to LCM will be 15 this will be X 307 into 3 + 7 and 25 that
is 21 + 45 upon 15 that will be equal to 56 upon 15 Now since we have to give answer in mixed fraction in whole number and fraction this a bi bi can be divided into a whole number and fraction part when divided by be the remainder is remainder is written here b is written here and question is written here so 56 by 15 can be written as 15 and 23 is 45 three years question remainder will be 11:00 that is 56 - 45 and below will be the denominator will be 15 so this is our answer and the correct
Which expression is equivalent to 5–√3⋅4–√5
5
3
⋅
4
5
?

Answers
The expression that is equivalent to ∛ 5 * \(\sqrt[5]{4}\) is \(5^{1/3}*4^{2/5}\)
What are radicals in math?A radical in mathematics is the opposite of an exponent, which is symbolized by the sign "n√" also known as root.
The number before the symbol or radical is regarded as an index number or degree, and it can either be a square root or a cube root and so on.
How to find the equivalent expressionThis equation represents exponents in fraction form and the basics for the calculation is from
x^(b/n)
\(\sqrt[n]{x}^{b}\)
Rewriting the expression is done as below
∛ 5
= \(5^{1/3}\)
and
\(\sqrt[5]{4}\)
\(= 4^{2/5}\)
combining both gives
∛ 5 * \(\sqrt[5]{4}\)
\(5^{1/3}*4^{2/5}\)
\(5^{1/3}*4^{2/5}\) is the equivalent expression
Learn more about exponents here:
https://brainly.com/question/29321719
#SPJ1
Sabas Company has 40,000 shares of $100 par, 1% preferred stock and 100,000 shares of $50 par common stock issued and outstanding. The following amounts were distributed as dividends: Year 1: $50,000 Year 2: 90,000 Year 3: 130,000 Determine the dividends per share for preferred and common stock for each year. If an answer is zero, enter '0'. Round all answers to two decimal places.
Answers
The dividends per share for preferred stock for each year are: Year 1 - $1.25, Year 2 - $2.25, Year 3 - $3.25. The dividends per share for common stock for each year are all $0.
To determine the dividends per share for preferred and common stock for each year, we need to divide the total dividends by the number of shares for each type of stock.
Preferred Stock:
Dividends per share of preferred stock = Total dividends for preferred stock / Number of preferred shares
Year 1:
Dividends per share of preferred stock for Year 1 = $50,000 / 40,000 shares = $1.25
Year 2:
Dividends per share of preferred stock for Year 2 = $90,000 / 40,000 shares = $2.25
Year 3:
Dividends per share of preferred stock for Year 3 = $130,000 / 40,000 shares = $3.25
Common Stock:
Dividends per share of common stock = Total dividends for common stock / Number of common shares
Year 1:
Dividends per share of common stock for Year 1 = ($50,000 - Total dividends for preferred stock) / 100,000 shares = ($50,000 - $50,000) / 100,000 shares = $0
Year 2:
Dividends per share of common stock for Year 2 = ($90,000 - Total dividends for preferred stock) / 100,000 shares = ($90,000 - $90,000) / 100,000 shares = $0
Year 3:
Dividends per share of common stock for Year 3 = ($130,000 - Total dividends for preferred stock) / 100,000 shares = ($130,000 - $130,000) / 100,000 shares = $0
The dividends per share for preferred stock for each year are: Year 1 - $1.25, Year 2 - $2.25, Year 3 - $3.25. The dividends per share for common stock for each year are all $0.
for more questions on stock
https://brainly.com/question/18124452
#SPJ8
What is the longest line segment that can be drawn in a right rectangular prism that is 15 cm long, 14 cm wide, and 9 cm tall?
Answers
152 sq+ 142 sq +92 sq
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
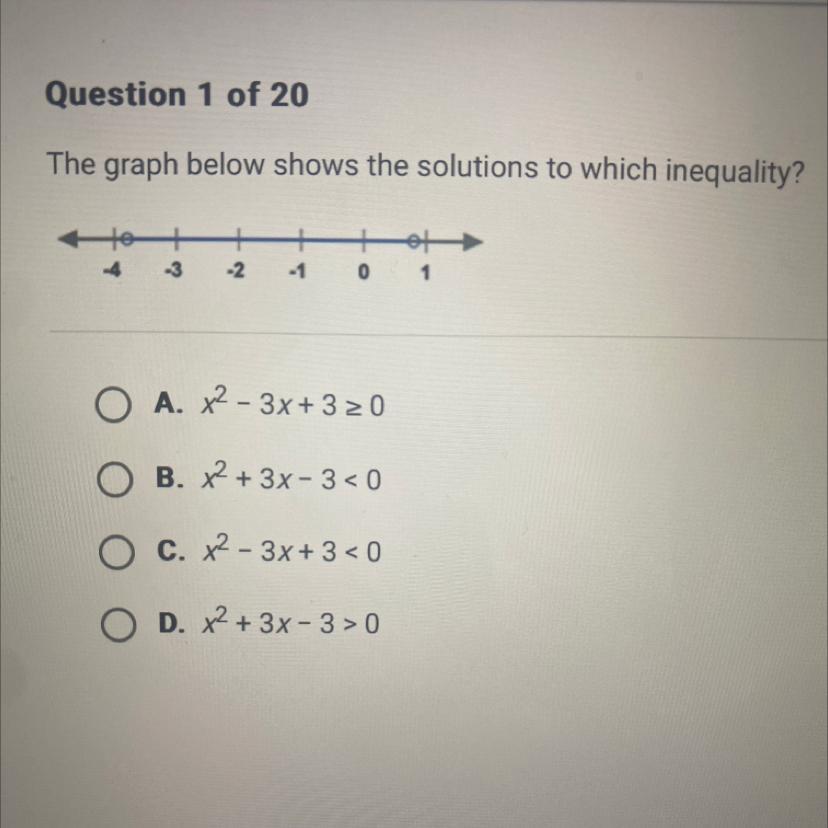
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
please help it's due tomorrow

Answers
Answer:
B. -414,720 x⁷y⁶
Step-by-step explanation:
To find the 4th term of the expansion of (2x - 3y²)¹⁰, we can use the binomial theorem.
The binomial theorem states that for an expression of the form (a + b)ⁿ:
\(\displaystyle (a+b)^n=\binom{n}{0}a^{n-0}b^0+\binom{n}{1}a^{n-1}b^1+...+\binom{n}{r}a^{n-r}b^r+...+\binom{n}{n}a^{n-n}b^n\\\\\\\textsf{where }\displaystyle \rm \binom{n}{r} \: = \:^{n}C_{r} = \frac{n!}{r!(n-r)!}\)
For the expression (2x - 3y²)¹⁰:
a = 2xb = -3y²n = 10Therefore, each term in the expression can be calculated using:
\(\displaystyle \boxed{\binom{n}{r}(2x)^{10-r}(-3y^2)^r}\quad \textsf{where $r = 0$ is the first term.}\)
The 4th term is when r = 3. Therefore:
\(\begin{aligned}\displaystyle &\;\;\;\;\:\binom{10}{3}(2x)^{10-3}(-3y^2)^3\\\\&=\frac{10!}{3!(10-3)!}(2x)^7(-3y^2)^3\\\\&=\frac{10!}{3!\:7!}\cdot2^7x^7(-3)^3y^6\\\\&=120\cdot 128x^7 \cdot (-27)y^6\\\\&=-414720\:x^7y^6\\\\ \end{aligned}\)
So the 4th term of the given expansion is:
\(\boxed{-414720\:x^7y^6}\)
which number is the best estimate of 866,214,000,000
Answers
This question is Incomplete because it lacks the appropriate options
Complete Question
Which number is the best estimate of 866,214,000,000 using powers of 10
a) 9 × 10¹¹
b) 8 × 10¹¹
c) 10 × 11¹⁰
d) 8 × 10-¹¹
Answer:
a) 9 × 10¹¹
Step-by-step explanation:
When we want to estimate a number using the power of 10, we are trying to write the number in a standard form.
We are to estimate :866,214,000,000 using powers of 10
Hence,
8.66214000000 × 10¹¹
We round up to the nearest whole number
= 9 × 10¹¹
Therefore, the best estimate for 866,214,000,000 using powers of 10
= 9 × 10¹¹
A line includes the points (1,9) and (4,24). What is the equation in slope-intercept form?
Answers
Answer:
y = 5x+4
Step-by-step explanation:
The slope-intercept form of an equation is like this:
y= mx+bM stands for the slope and b for the y-intercept.
First, we need to find the slope:
m= slope= y1-y2/ x1-x2m= slope= 9-24/1-4m= 5Now we know: y= 5x+b
Now, to find b we have to choose one of your points. Let's use the first given point: (1, 9)
With the slope-intercept form equation I showed before, substitute x and y with the values of one point.
9= 5(1)+b9= 5+b9- 5= 5-5+b4= bSubstitute the b in the equation, and that's your answer:
y= 5x+4Evaluate x^4 • x^-2 when x = 5
Answers
Answer:
x^4 • x^-2 = x^6
Step-by-step explanation:
faste او انوار کو کسی Q2. 3 balls are drawns from the box containing six white balls five red balls and four blue balls find the probabi- lity. that they are draw from the other blue red and white if each ball is (i) Replaced (ii) Not replace.
Answers
The probability of drawing blue, red, and white balls consecutively is 120/3375 with replacement and 120/2730 without replacement.
To calculate the probability of drawing three balls from a box containing six white balls, five red balls, and four blue balls, we need to consider two scenarios: with replacement and without replacement.
(i) With replacement:
When each ball is replaced after it is drawn, the total number of balls remains the same for each draw. Therefore, the probability of drawing a specific color on each draw remains constant.
The probability of drawing a blue ball on each draw is 4/15, the probability of drawing a red ball is 5/15, and the probability of drawing a white ball is 6/15 (assuming all colors are equally likely to be drawn).
To find the probability of drawing a blue, red, and white ball consecutively, we multiply the probabilities together since the events are independent:
P(Blue, Red, White) = (4/15) * (5/15) * (6/15) = 120/3375
(ii) Without replacement:
When the balls are not replaced after being drawn, the total number of balls decreases for each subsequent draw. This affects the probability of each color being drawn on subsequent draws.
For the first draw, the probability of drawing a blue ball is 4/15, a red ball is 5/15, and a white ball is 6/15.
For the second draw, the probability of drawing a blue ball is 3/14, a red ball is 5/14 (as one blue ball is already drawn), and a white ball is 6/14.
For the third draw, the probability of drawing a blue ball is 2/13, a red ball is 4/13 (as two blue balls and one red ball are already drawn), and a white ball is 6/13.
To find the probability of drawing a blue, red, and white ball consecutively without replacement, we multiply the probabilities together:
P(Blue, Red, White) = (4/15) * (5/14) * (6/13) = 120/2730
Therefore, the probability of drawing blue, red, and white balls consecutively is 120/3375 with replacement and 120/2730 without replacement.
for similar questions on Probability.
https://brainly.com/question/25839839
#SPJ8
A cylinder has a volume of 659.4 cubic centimeters. The diameter of the cylinder is 10 cm. What is the height of the cylinder?
(Assume = 3.14)
A.
42 cm
B.
2.1 cm
C.
8.4 cm
D.
21 cm
Answers
The height is 8.4.
Calculated with H = V / πr^2, with H for height, V for volume, and r for radius (the diameter divided by 2).
A bag of snacks contains 3 flavors: cherry, lemon, and grape. Carol will take 1 snack from the bag without looking. The probability for each flavor is shown in the table.

Answers
Middle - cherry
Most likely - grape
Please help me determine the general equation for the graph above as well as solve for a. Thank you.

Answers
Observe that the x coords of the roots of a polynomial are,
\(x_{1,2,3,4}=\{-3,0,1,4\}\)
Which can be put into form,
\(y=a(x-x_1)(x-x_2)(x-x_3)(x-x_4)\)
with data
\(y=a(x-(-3))(x-0)(x-1)(x-4)=ax(x+3)(x-1)(x-4)\)
Now if I take any root point and insert it into the equation I won't be able to solve for y because they will always multiply to zero (ie. when I pick \(x=-3\) the right hand side will multiply to zero,
\(y=-3a(-3+3)(-3-1)(-3-4)=0\)
and a will be "lost" in the process.
If we observed a non-root point that we could substitute with x and y and result in a non-loss process then you could find a. But since there is no such point (I don't think you can read it of the graph) there is no other viable way to find a.
Hope this helps :)
what is the degree of the polynomial 5x+7
Answers
Answer:
1
Step-by-step explanation:
The degree of a polynomial is the highest power of the variable in the polynomial. In this case, the highest power of the variable is 1, so the degree of the polynomial 5x+7 is 1.
For example, the polynomial 2x^2 + 3x + 4 has a degree of 2 because the highest power of the variable x is 2. The polynomial x^3 + x + 1 has a degree of 3 because the highest power of x is 3
Answer:
it is 1
Step-by-step explanation:
because it is only one x there
You are given: (i) The future lifetimes of (40) and (50) are independent. (ii) The survival function for (40) is based on a constant force of mortality, u = 0.05. (iii) The survival function for (50) is So(x) = 1 - x/10 (De Moivre's Law with w=110). Calculate the probability that (50) dies within 10 years and dies after (40). A) Less than .02 B) At least .02 but less than .04 C) At least .04 but less than .06 D) At least .06 but less than .08 E) At least.08 Select one: A. Less than .02 B. At least .02 but less than .04 C. At least.04 but less than 06 D. At least.06 but less than 08 E. At least .08
Answers
The probability that (50) dies within 10 years and dies after (40) is at least 0.02 but less than 0.04. So the answer is B. At least .02 but less than .04.
To calculate the probability that (50) dies within 10 years and dies after (40), we need to find the joint probability of the two events happening together.
Let X and Y be the future lifetimes of (40) and (50), respectively. We want to find P(Y≤10 and X<Y). Using the Law of Total Probability, we can write:
P(Y≤10 and X<Y) = ∫P(Y≤10 and X<Y|X=t) fX(t)dt
where fX(t) is the probability density function of X.
Since the force of mortality for (40) is constant, the probability density function for X is given by:
f X (t)=ue −ut
where u=0.05.
For (50), we have the survival function S(y) = 1 - y/10. So, the probability density function for Y is:
fY(y) = S'(y) = 1/10
Now, we can substitute these expressions into the integral and simplify:
P(Y≤10 and X<Y) = ∫P(Y≤10 and X<Y|X=t) fX(t)dt
= ∫∫P(Y≤10 and X<Y|X=t) fY(y)fX(t)dydt
= ∫∫P(Y≤10 and t<Y) (1/10)(0.05)e^(-0.05t)dydt
= (1/10)∫e^(-0.05t) ∫1≤y≤10 e^(0.1y) dydt
= (1/10)∫e^(-0.05t) (e - e^(-t/10)) dt
Evaluating this integral, we get:
P(Y≤10 and X<Y) ≈ 0.0286
Find out more about the Law of Total Probability
at brainly.com/question/14315459
#SPJ4
Need help with this have no idea how to do it

Answers
Answer:
Step-by-step explanation:
x- intercept, vertex (v) and axis of symmetry, parabola form:x²+bx+c
vertex(h,k)
1- f(x)=(x+3)(x-3) change into parabola formf(x)=x²-9 a=1,b=0 ,c=-9
h=-b/2a=0
k=f(0)=-9
vertex(0,-9) , x intercept is when f(x)=0
(x-3)(x+3)=0 either x-3=0⇒ x=3 or x+3=0 then x=-3
x=3, x=-3 (-3,0) and (3,0)
the x of symmetry is the h of the vertex=0
2-g(x)=(x+1)(x-3)g(x)=x²-2x-3 a=1, b=-2,c=-3
h=-b/2a⇒-(-2)/2(1)⇒h=1
k=f(1)=1²-2(1)-3⇒k=-4
v(1,-4)
x of symmetry=h=1
(x+1)(x-3)=0
x+1=0⇒x=-1 (-1,0)
x-3=0 ⇒x=3 (3,0)
x intercept :-1,3
3-y=-x(x+6) ⇒y=-x²-6x a=-1,b=-6, c=0vertex(-3,9)
x intercept:(0,0) and (-6,0)
axis of symmetry =-3
4-g(x)=2(x-5)(x-1) ⇒ 2x²-12x+10 a=2, b=-12, c=10vertex(3,-8)
axis of symmetry=3
x intercept : (5,0), (1,0)
5) -4x(x+1)⇒-4x²-4x a=-4,b=-4vertex(-1/2,1)
x of symmetry=-1/2
x intercept : (0,0)(-1,0)
6- f(x)=-2(x-3)² ⇒-2x²+12x-18vertex(3,0)
x intercept (3,0)
axis of symmetry = 3





15 = -5x + 10
X =
Pls help me solve x
Answers
Step-by-step explanation:
\(15 = - 5x + 10 \\ - 5x = 15 - 10 \\ - 5x = 5 \\ x = \frac{5}{ - 5} \\ x = - 1 \\ thank \: you\)
The first shelf on Hannah’s bookshelf hoods an equal number of fiction and nonfiction. If Hannah’s selects 5 books randomly, what is the probability that 3 of the books will be fiction and 2 will be nonfiction
Answers
Answer:
The correct option is (D) one of the non-fiction books on the bottom shelf and a second non-fiction book from the bottom shelf.
Step-by-step explanation:
What is probability?
Probability is the branch of mathematics that deals with numerical descriptions of how probable an event is to occur or how likely it is that a claim is true.
To find which 2 books describe a pair of dependent events:
A pair of two dependent events are simply those in which the selection of the second item is contingent on the selection of the first item, causing the probability to change.
Because the sample size is lowered when the initial item is taken without replacement, choosing the exact same item reduces the chance.
Now, in regard to the question, this means that for two of the occurrences to be independent, they must be on the same shelf and of the same type of book, so that the second book cannot be selected until the first one is.
Option D, where both books are on the same shelf and are of the same type, is the only option that fulfills this requirement.
Therefore, the correct option is (D) one of the non-fiction books on the bottom shelf and a second non-fiction book from the bottom shelf.
Know more about probability here:
brainly.com/question/25870256
#SPJ4
Examine the following expression.
p squared minus 3 + 3 p minus 8 + p + p cubed
Which statements about the expression are true? Check all that apply.
The constants, –3 and –8, are like terms.
The terms 3 p and p are like terms.
The terms in the expression are p squared, negative 3, 3 p, negative 8, p, p cubed.
The terms p squared, 3 p, p, and p cubed have variables, so they are like terms.
The expression contains six terms.
The terms p squared and p cubed are like terms.
Like terms have the same variables raised to the same powers.
The expression contains seven terms.
Answers
Answer:
the terms in the expression are p squared, negative 3,3p, negative 8,p,p cubed
Step-by-step explanation:
hope that helps
a 2.0-cm-tall object is 15 cm in front of a plano-convex polystyrene plastic lens that has a 13 cm radius of curvature. what are the (a) position and (b) height of the image
Answers
The position of the image is 42.25 cm in front of the lens. and its height is 5.64 cm and inverted.
We can use the thin lens equation to find the position of the image:
\(1/f = 1/d_o + 1/d_i\)
where f is the focal length of the lens, \(d_o\) is the object distance (distance between object and lens), and \(d_i\) is the image distance (distance between image and lens). We can solve for \(d_i\):
\(1/d_i = 1/f - 1/d_o\)
f = R/2 for a plano-convex lens with radius of curvature R, so in this case
\(f = 13 cm/2 = 6.5 cm\).
Plugging in \(d_o\) = 15 cm and f = 6.5 cm, we get:
\(1/d_i = 1/6.5 - 1/15\\1/d_i = 0.1538\\d_i = 6.5/0.1538\\d_i = 42.25 cm\)
So the position of the image is 42.25 cm in front of the lens.
To find the height of the image, we can use the magnification equation:
\(m = -d_i/d_o\)
where m is the magnification (negative for a virtual image), \(d_i\) is the image distance (which we just found), and \(d_o\) is the object distance (given as 15 cm).
\(m = -42.25/15\\m = -2.82\)
This means that the image is 2.82 times smaller than the object. Since the object is 2.0 cm tall, the height of the image is:
\(h_i = mh_o\\h_i = -2.822.0 cm\\h_i = -5.64 cm\)
The negative sign indicates that the image is inverted (upside down). So the position of the image is 42.25 cm in front of the lens, and its height is 5.64 cm and inverted.
For more question on lens equation click on
https://brainly.com/question/25020197
#SPJ4
Stock purchase for $170 is now worth $251 what is the percentage increase of value
Answers
Answer:
47.647% Increase
Step-by-step explanation:
You need to find the amount it increased by first, so
251-170=81
Then you need to find what percent of 170 that is, so
81/170=0.47647
Finally multiply that by 100 to get the percent:
0.47647×100=47.647%
valuate the summation for the indicated value of the variable. 1(1!) + 2(2!) + 3(3!) + 4(4!) + m(m!); m = 3
Answers
The answer of the given question based on the expression is , the value of the summation when m = 3 is 137.
What is Expression?In mathematics, an expression is a combination of numbers, variables, and operators that represents a value or a set of values. It can be a simple combination of numbers and variables or a more complex combination involving mathematical operations like addition, subtraction, multiplication, division, exponents, and roots. Expressions can be used to represent a wide range of mathematical concepts, from simple arithmetic to complex functions and equations.
To evaluate the summation 1(1!) + 2(2!) + 3(3!) + 4(4!) + m(m!), where m = 3, we substitute m = 3 and simplify:
1(1!)+2(2!) +3(3!) +4(4!) +3(3!)
= 1(1) + 2(2) + 3(6) + 4(24) + 3(6) (since n! = n(n-1)! for all positive integers n)
= 1 + 4 + 18 + 96 + 18
= 137
Therefore, the value of the summation when m = 3 is 137.
To know more about Variables visit:
https://brainly.com/question/2466865
#SPJ1
Drag the tiles to the correct locations on the image. Not all the tiles will be used.
The figure is a square, with side lengths as shown.
4√5mm
What are the perimeter and area of the square
Answers
The perimeter of the square is 16√5 mm, and the area of the square is 80 mm².
To calculate the perimeter and area of the square, we can use the formulas:
Perimeter = 4 * side length
Area = side length * side length
Substituting the given side length of 4√5mm into the formulas, we have:
Perimeter = 4 * 4√5mm = 16√5mm
Area = (4√5mm) * (4√5mm) = 16 * 5mm = 80mm²
Therefore, the perimeter of the square is 16√5mm, and the area of the square is 80mm².
Please note that the values are based on the provided side length of 4√5mm. If there are any changes to the side length, the perimeter and area will differ accordingly.
For such more question on perimeter:
https://brainly.com/question/397857
#SPJ8
The perimeter of the square is 16√5 mm, and the area of the square is 80 mm².
I took the test on plato.
The perimeter of a rectangle is 44 meters and the length is 10 meters more than twice the width. Find the dimensions.
A: 18 meters and 4 meters
B: 6 meters and 9 meters
C: 5 meters and 9 meters
D: 6 meters and 16 meters
Answers
Answer:
Width of rectangle = 4 meter
Length of rectangle = 18 meter
Step-by-step explanation:
Given:
Perimeter of rectangle = 44 m
Assume;
Width of rectangle = a
Length of rectangle = 2a + 10
Find:
Length and width
Computation:
Perimeter of rectangle = 2[l + b]
2[a + 2a + 10] = 44
3a + 10 = 22
3a = 12
a = 4
So,
Width of rectangle = a = 4 meter
Length of rectangle = 2a + 10 = 18 meter
35 points
(algebra one)
describe and correct the error in comparing the graphs
