Answers
Answer:
y = 3x + 6
Step-by-step explanation:
(-1, 3) --> (0, 6) --> (1, 9) --> (2, 12) --> (3, 15) --> (4, 18)
3 is the slope and 6 is the y-intercept
The 3 is the slope and the 6 is the y intercept.
Related Questions
For the attached graph two questions:
1. What does the slope of the line represent, in context of the problem?
2. What does the y intercept represent, in context of the problem?

Answers
The slope of the line represents the speed in miles per hour
The y intercept represents the initial distance
What does the slope of the line representfrom the question, we have the following parameters that can be used in our computation:
The graph
Where, we have
x = time in hours
y = distance in miles
The slope is
slope = change in y/x
So, we can conclude that the slope is the speed
What does the y intercept representBy definition, the y intercept is the initial value of the graph
In this case;
y intercept = initial distance
Read more about linear relation at
https://brainly.com/question/30318449
#SPJ1
Data Set 1 has a mean of 54 and a MAD of 4. Data Set 2 has a mean of 60 and a MAD of 2.
What can be concluded about the two distributions?
Select each correct answer.
A} The distributions are similar.
B} The distributions are somewhat similar.
C} The means-to-MAD ratio is 3.
D} The means-to-MAD ratio is 1.5.
Answers
The correct option about the two data set's distribution is B) The distributions are somewhat similar.
Given that,
For data set 1,
Mean = 54 and MAD = 4
For data set 2,
Mean = 60 and MAD = 2
Means to MAD ratio = (60 - 54) / (2 - 4) = 6 / -2 = -3
So means to MAD ratio is -3, not 3.
Now, it is clear that the distributions are not fully similar.
But it appears to be somewhat similar since Mean absolute deviation is somewhat similar, which is close.
Hence the correct option is B.
Learn more about Data Distributions here :
https://brainly.com/question/14926605
#SPJ1
2. A coffee maker and a juice maker are making beverages. The rate at
which the coffee is being made is given by y = 6x, where y represents the
amount of coffee in mL and x represents the time passed in seconds. The
amount of juice that has been made at different times is summarized in
the table.
thing Company
A. At what rate is the coffee maker making coffee?
B. At what rate is the juice maker making juice?
C. Is juice or coffee being made at a faster rate?
Time (s)
0
1
2
3
Juice (mL)
0
8
16
24
Answers
(A) The rate of making coffee by coffee maker is 6 mL/second.
(B) The rate of making juice by juice maker is 8 mL/second.
(C) Juice is being made at a faster rate.
What is ratio?Ratio basically compares quantities, that means it show value of one quantity with respect to other quantity.
If a and b are two values, their ratio will be a:b,
Given that,
The rate of coffee made by coffee maker is represented by,
y = 6x (1)
Here, y represents the amount of coffee in mL and x represents the time passed in seconds.
Also, The rate of juice made by juice make can be represented by the given table as,
k = 8h (2)
Here, k represents the amount of juice in mL and h represents the time passed in seconds.
(A)
To find the rate of making coffee, solve the equation (1),
y = 6x
⇒ y/x = 6 mL/second
The rate of making coffee by coffee maker is 6 mL/second.
(B)
To find the rate of making juice, solve the equation (2),
k = 8h
⇒ k/h = 8 mL/second
The rate of making juice by juice maker is 8 mL/second.
(C)
Since, the juice is made at the rate of 8 mL/second and the coffee is made at the rate of 6 mL/second.
Therefore, juice is being made at a faster rate.
To know more about Ratio on:
https://brainly.com/question/23724140
#SPJ1
I am stuck please help with this graph.
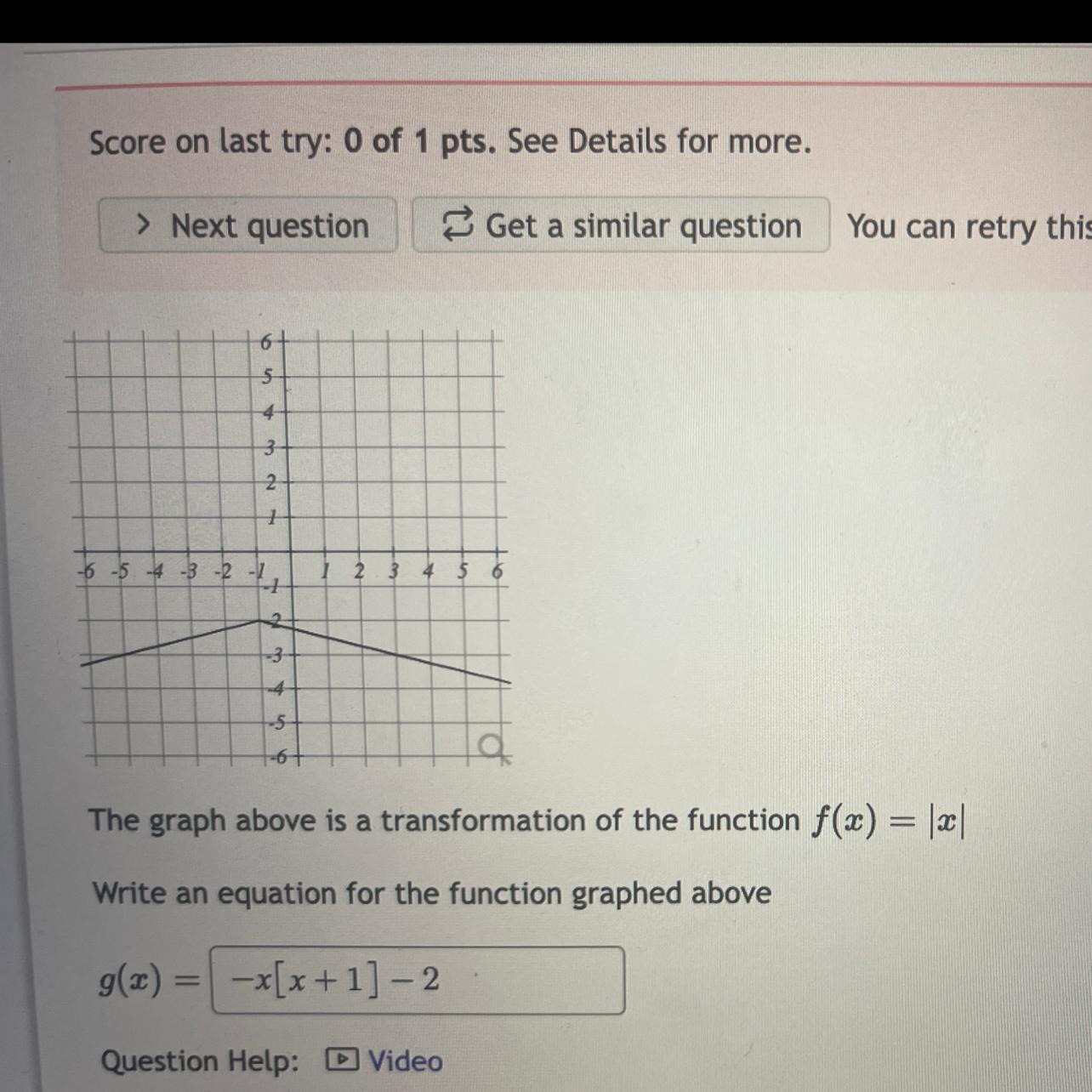
Answers
An equation for the function graphed above include the following: g(x) = -1/4|x + 1| - 2.
How to interpret and determine the equation of g(x)?By critically observing the graph of this absolute value function, we can reasonably infer and logically deduce that the parent absolute value function f(x) = |x| was vertically compressed by a factor of 1/4, reflected over the x-axis, followed by a vertical translation 2 units down, and then a horizontal translation to the left by 1 unit, in order to produce the transformed absolute value function as follows;
f(x) = |x|
y = A|x + B| + C
g(x) = -1/4|x + 1| - 2
In conclusion, the value of the variables A, B, and C are -1/4, 1, and 2 respectively.
Read more on absolute value function here: brainly.com/question/28308900
#SPJ1
I need help with this!

Answers
The length AC in the kite is 8.7 cm.
How to find the side AC in the kite?A kite is a quadrilateral that has two pairs of consecutive equal sides and
perpendicular diagonals. Therefore, let's find the length AC in the kite.
Hence, using Pythagoras's theorem, let's find CE.
Therefore,
7² - 4² = CE²
CE = √49 - 16
CE = √33
CE = √33
Let's find AE as follows:
5²- 4² = AE²
AE = √25 - 16
AE = √9
AE = 3 units
Therefore,
AC = √33 + 3
AC = 5.74456264654 + 3
AC = 8.74456264654
AC = 8.7 units
learn more on kite here: https://brainly.com/question/27975644
#SPJ9
Nina's garden 4 1/5 meters long and 3/10 meter wide. What is the area of Nina's garden?
Answers
Answer:
63/50 as an improper fraction.
1 13/50 as a mixed number
Step-by-step explanation:
On a piece of paper, graph y ≥ 2x – 3. Then determine which answer choice matches the graph you drew.
Answers
Answer:
Step-by-step explanation:
We are asked to graph an inequality . y≥2x - 3
The boundary line of our given inequality will be a solid line as we have greater than or equal to ≥ sign.
The boundary line of our given inequality would be .y=2x - 3
Now, we will test point (0,0) to shade in the correct region as:
0≥2(0)-3
0≥0-3
0≥-3
It should look something like this:

A suit was marked with a 10% discount.
If the discount is $16.00, what was the original price of the suit?
Answers
Answer:
See below:
Step-by-step explanation:
Hello! My name is Galaxy and I will be helping you today. I hope you are having a nice day.
We can solve the problem in 2 steps, one being Solving and the other being Comprehending. I'll start off with comprehending.
Comprehending
So, we know that 10% of a number is $16. That means that \(\frac{1}{10}\) of the number "\(x\)" is equal to $16.
A percentage is basically a fraction of something, for example, 25% of a number would be \(\frac{1}{4}\) of the same number.
Example:
25% of 10 = \(\frac{1}{4} * 10 = 2.5\)
2.5 is 25% of 10 = \(2.5 \div \frac{1}{4}=10\)
Now that we know the basics, we can do the real solving.
Solving
To solve, the question, we can first read the problem and make an equation,
"10% of \(x\) is 16."
We can then make a equation.
\(x(\frac{1}{10})=16\)
\(x=16 \div \frac{1}{10} \\x=160\)
After solving, we know that 10% of 160 is equal to 16. We can prove that with the following:
\(16*10=160\)
After solving our equation, we can see that the answer is $160.
$16 is 10% of $160.
Cheers!
Which of the expressions are equivalent to the one below check all that apply

Answers
Answer:
A , B and C
Step-by-step explanation:
evaluate the expressions following the order of operations as set out in PEMDAS
initial expression
note that • indicates multiplication
3 (2 + 6) + 4 × 5 ← evaluate parenthesis
= 3(8) + 20 = 24 + 20 = 44
A
5 × 4 + 3 × (6 + 2) ← evaluate parenthesis
= 5 × 4 + 3 × 8 ← perform multiplication
= 20 + 24 ← perform addition
= 44
B
(6 + 2) × 3 + 4 × 5 ← evaluate parenthesis
= 8 × 3 + 4 × 5 ← perform multiplication
= 24 + 20 ← perform addition
= 44
C
3 × 2 + 3 × 6 + 4 × 5 ← perform multiplications
= 6 + 18 + 20 ← perform addition
= 44
D
3 × 2 + (6 + 4) × 5 ← evaluate parenthesis
= 3 × 2 + 10 × 5 ← perform multiplication
= 6 + 50 ← perform addition
= 56
the expressions equivalent to the initial expression are A , B and C
Andrea is told that the means of two groups in a study were statistically significant. She knows the means and standard deviations of the two groups and is interested in calculating an estimate of effect size. Given this information, which effect size estimate should she calculate
Answers
Answer:
Cohen's D
Step-by-step explanation:
Cohen's D is a statistic that measures effect size. It shows standardised difference between 2 means.
Effect size is defined as how large the effect of a something is or its magnitude.
Cohen's D works effectively when the sample is >50 (that is for large samples). However a correction factor can be used to make results from small samples more accurate
The formular for Cohen's D is:
D = (mean1 - mean2) ÷ (√({standard deviation1}^2 + {standard deviation 2}^2)/2)
This is the most appropriate method in the given scenario
With the aid of an illustration from a well labelled diagram, explain a cross over experimental design using a scenario with three treatment
Answers
A crossover design is a reiterated assessments design in which each experimental unit (patient) receives various treatments at different time periods, i.e., the patients switch from one therapy to another during the trial.
What is the advantage of a crossover design?The crossover design has the benefit of each subject acting as his or her own control, and it requires a lesser number of patients than parallel-group trials.
There are various drawbacks. For example, crossover designs often last longer than parallel-group research.
Learn more about experiments at;
https://brainly.com/question/16286146
#SPJ1

Factor this polynomial completely\(15 {x}^{2} - 11x - 12\)
Answers
Given:
The polynomial
\(15x^2-11x-12\)Required:
Factor this polynomial completely.
Explanation:
We will solve as:
\(\begin{gathered} 15x^2-11x-12 \\ 15x^2-20x+9x-12 \\ 5x(3x-4)+3(3x-4) \\ (5x+3)(3x-4) \end{gathered}\)Answer:
Factor of polynomial is (5x + 3)(3x - 4).
How do I find the value

Answers
A = 139°
B = 139°
You can see A and B are coefficients of each other, which means they have the same angle because they are opposite each other on the straight line. just like the two 41° angles are.
The angle around a point always add up to 360°, so add the 41° angles.
41 + 41 = 82°
Then minus this by 360°.
360 - 82 = 278°
And to work out one angle, which gives you the angle for both, divide 278 by two.
278 ÷ 2 = 139°
Both A and B have an angle of 139°
Example:
To find the value of two intersecting lines, you need to know the equations of both lines. Then, you can set the equations equal to each other and solve for the variable x. This will give you the x-coordinate of the point where the lines intersect. To find the y-coordinate, you can plug the value of x into either equation and solve for y. For example, if one line is y = 3x - 5 and another line is y = -2x + 7, then you can set 3x - 5 = -2x + 7 and solve for x:
3x - 5 = -2x + 7
5x = 12
x = 12/5
Then, plug x = 12/5 into either equation and solve for y:
y = 3(12/5) - 5
y = 36/5 - 25/5
y = 11/5
Therefore, the point of intersection is (12/5, 11/5).
If one of the lines has a given angle, such as 41 degrees, then you can use trigonometry to find its equation. For example, if one line passes through the origin and has an angle of 41 degrees with the positive x-axis, then you can use the slope formula to find its equation:
slope = tan(41 degrees) ≈ 0.87
y = mx + b
y = 0.87x + 0
Then, you can use the same method as before to find the point of intersection with another line.
_______________________________________________________
The answer is 139 degrees, using the method I gave.
MARK AS BRAINLIEST!!!
Write as a product: c^3-c^4+2c^5
PLEASE HELP!!!
Answers
Answer:
\(c^3-c^4+2c^5\) \(= c^3 * (1 - c + 2c^2)\)
Step-by-step explanation:
Given
\(c^3-c^4+2c^5\)
Required
Write as product
\(c^3-c^4+2c^5\)
Expand the above expression
\(c^3-c^3*c+2c^3*c^2\)
Factorize:
\(c^3(1 -c+2c^2)\)
The expression in bracket can not be further factorized.
Hence:
\(c^3-c^4+2c^5\) \(= c^3 * (1 - c + 2c^2)\)
Given the function f(x) = −3x2 + 4x + 6, find f(2) and f(3). Choose the statement that is true concerning these two values.
The value of f(2) is the same as the value of f(3).
The value of f(2) cannot be compared to the value of f(3).
The value of f(2) is smaller than the value of f(3).
The value of f(2) is larger than the value of f(3).
Question 15(Multiple Choice Worth 1 points)
(02.03 MC)
A telephone company charges a fixed monthly rate plus a rate per megabyte of data used. The company charges $135 for 100 megabytes of data and $375 for 500 megabytes of data. An equation can be written to show the relationship between the total megabytes used (x) and the total monthly charges (y). Which of the following best describes the steps to draw the graph?
Draw a graph that joins the points (135, 100) and (375, 500) and has a slope = 0.6
Draw a graph that joins the points (100, 135) and (500, 375) and has a slope = 0.6
Draw a graph that joins the points (100, 135) and (500, 375) and has a slope = 1.67
Draw a graph that joins the points (135, 100) and (375, 500) and has a slope = 1.67
Answers
Answer:
(B) Draw a graph that joins the points (100, 135) and (500, 375) and has a slope = 0.6
Step-by-step explanation:
1. They gave us two points
(100, 135)
(500, 375)
2. We find the formula
(375, 135)
(500,100) which is 0.6
~~Hope this helps~~
Simplify 4x²y + 12z² + 6x²y – 2z.
10x²y + 12z² - 2z
10x²y + 14z²
20x²yz²
10x²y + 10z²
Answers
Answer:
Group the like terms together:
4x²y + 6x²y + 12z² - 2z
Simplify:
10x²y + 12z² - 2z
The simplified expression is 10x²y + 12z² - 2z.
Step-by-step explanation:
Answer:
The simplified expression is 10x²y + 12z² - 2z
Step-by-step explanation:
To simplify the expression, we combine like terms, which are terms that have the same variables raised to the same powers. In this case, we have two terms with the variable 4x²y and two terms with the variable -2z. We can combine these like terms by adding their coefficients:
4x²y + 6x²y = 10x²y
-2z + (-2z) = -4z
So the expression simplifies to:
10x²y + 12z² - 4z
We can further simplify this expression by combining the terms with the variable z:
12z² - 4z = 4z(3z - 1)
Therefore, the final simplified expression is:
10x²y + 4z(3z - 1)
We can also write this expression as:
10x²y + 12z² - 2z
which is the answer provided.
Solve
-3(2x+1)= 4(x-1)
Answers
Answer: x = 1/0 in exact form. x = 0.1 in decimal form.
First step, distribute:
\(-6x-3 = 4x-4\)
Next, isolate x to one side :
\(-6x - 4x=-4+3\)
\(-10x=-1\)
Last step, divide both sides by -10:
\(x=\frac{1}{10}\)
Thus, the answer is \(\frac{1}{10}\)
Hope this helped :)
Let D be a region bounded by a simple closed path C in the xy-plane. The coordinates of the centroid x, y of D are x = 1 2A x2 dy C y = ? 1 2A y2 dx C where A is the area of D. Find the centroid of a quarter-circular region of radius a.
Answers
If D be a region bounded by a simple closed path C in the xy-plane, then the centroid of the quarter circle is (4a/3π , 4a/3π) .
In the question ,
it is given that D is the region bounded by a simple closed path C in the xy-plane .
the radius of the circle is = "a" ,
let the equation of the circle be x² + y² = a² ,
So , the area of the quarter circle is (A) = (1/4)*πa²
The coordinate of the centroid x will be :
x = \(\frac{1}{2A} \int\limits x^{2} dy\)
x = \(\frac{1}{2(\frac{\pi a^{2} }{4})} \int\limits^a_0 {a^{2} -y^{2} } \, dy\)
Simplifying further ,
we get ,
x = 2/πa² [{a²(a) - a³/3} - 0 ]
x = 2/πa² [a³ - a³/3 ]
x = 4a/3π
The coordinate of the centroid y will be :
y = \(\frac{1}{2A} \int\limits y^{2} dx\)
y = \(\frac{1}{2(\frac{\pi a^{2} }{4})} \int\limits^a_0 {a^{2} -x^{2} } \, dx\)
Simplifying further ,
we get ,
y = 2/πa² [{a²(a) - a³/3} - 0 ]
y = 2/πa² [a³ - a³/3 ]
y = 4a/3π
Therefore , the coordinates of the centroid is (4a/3π , 4a/3π) .
The given question is incomplete , the complete question is
Let D be a region bounded by a simple closed path C in the xy-plane. The coordinates of the centroid x, y of D are x = \(\frac{1}{2A} \int\limits x^{2} dy\) , y = \(\frac{1}{2A} \int\limits y^{2} dx\) ?
Find the centroid of a quarter-circular region of radius a.
Learn more about Centroid here
https://brainly.com/question/5872501
#SPJ4
Megan goes on walking holiday for five days.
The table shows how far she walked on the first four days.
Monday-14km,Tuesday-23km,Wednesday-13km,Thursday-13km
Megan says,'My average for the first four days is more than 15km.'
Explain why Megan is correct.
Friday is her last day.
She wants to increase her average to 17 km.
How many kilometres must she walk on Friday?
Answers
Answer:
a) Megan's total so far is 3 km more than necessary for an average of 15 km
b) 22 km
Step-by-step explanation:
a) The total of differences from 15 is ...
-1 + 8 + (-2) +(-2) = 3
Since this is more than 0, Megan's average is more than 15.
__
b) The total of differences from 17 is ...
-3 +6 -4 -4 = -5
To increase her average to 17 km, Megan must walk 17+5 = 22 km on Friday.
_____
Comment on the approach
In general, I find it easier mentally to deal with small numbers than with larger ones. So adding small differences can be easier than computing larger sums.
a) By computing the difference from the supposed average, we have effectively found the difference of the sum of values from the total necessary to give the required average. That is, Megan's average would be 15 if her total distance were 4·15 = 60. Her total distance is (4·15 +3) = 63, so her average is more than 15.
b) By finding out how much the total is below that necessary for the desired average, we determine the amount above that average the final number needs to be.
(14 -17) +(23 -17) +(13 -17) +(13 -17) +(Friday -17) = 0 . . . . the Friday value to make an average of 17
14 +23 +13 +13 +Friday = 5·17 . . . . . . . add 5·17
(14 +23 +13 +13 +Friday)/5 = 17 . . . . . . shows the Friday amount gives the required average
Friday = 17 -((14 -17) +(23 -17) +(13 -17) +(13 -17)) . . . . first equation rearranged to show how we computed Friday
Friday = 17 -(-5) = 17 +5 = 22
Problem 3.4 (Video 2.5 - 2.6, Lecture Problem) You are interested in calculating the probability that your favorite 1
Game of Thrones character is eliminated in episode X. You have decided to model X as a Geometric (1/4) random variable. (a) Unfortunately, you have learned a spoiler: your favorite character does not appear in episode 4 or beyond. What is the conditional PMF P X∣B
(x) of X given the event B={X<4} ? (b) Given this spoiler, what is the probability that your favorite character is eliminated in one of the first two episodes? (c) Given this spoiler, what is the expected value of X conditioned on the event B ? (d) Let's consider yet another scenario: After watching the show for 2 episodes, you are happy to see that your favorite character has not been eliminated yet. What is the conditional PMF P X∣C
(x) of X given the event C={X>2} ? 1
Somehow, you have already managed to decide on a favorite character before watching any episodes. 2 (e) Let Y=X−2 be the number of additional episodes after the 2 nd that it takes for your favorite character to be eliminated. Using part (d), quickly determine the conditional PMF P Y∣C
(y) of Y given the event C={X>2}. Determine the family of random variables this conditional PMF belongs to, along with the associated parameter(s). (f) Using what you learned in part (e), determine the conditional mean E[X∣C].
Answers
(a) The conditional PMF P X∣B (x) of X given the event B={X<4} can be calculated using the formula
P(X=x|B) = P(X=x and B)/P(B).
Since the event B={X<4} includes the events X=1, X=2, and X=3, we can calculate P(B) as the sum of the probabilities of these events:
P(B) = P(X=1) + P(X=2) + P(X=3) = (1/4) + (3/4)(1/4) + (3/4)^2(1/4) = 13/16.
Therefore, the conditional PMF P X∣B (x) is given by:
P(X=1|B) = P(X=1 and B)/P(B) = (1/4)/(13/16) = 4/13
P(X=2|B) = P(X=2 and B)/P(B) = (3/4)(1/4)/(13/16) = 3/13
P(X=3|B) = P(X=3 and B)/P(B) = (3/4)^2(1/4)/(13/16) = 6/13
(b) The probability that your favourite character is eliminated in one of the first two episodes given the spoiler is P(X=1|B) + P(X=2|B) = 4/13 + 3/13 = 7/13.
(c) The expected value of X conditioned on the event B can be calculated using the formula E[X|B] = sum(x*P(X=x|B)) for all x in the support of X. Therefore, E[X|B] = 1*(4/13) + 2*(3/13) + 3*(6/13) = 20/13.
(d) The conditional PMF P X∣C (x) of X given the event C={X>2} can be calculated using the formula P(X=x|C) = P(X=x and C)/P(C). Since the event C={X>2} includes the events X=3, X=4, ..., we can calculate P(C) as the sum of the probabilities of these events: P(C) = P(X=3) + P(X=4) + ... = (3/4)^2(1/4) + (3/4)^3(1/4) + ... = (3/4)^2/(1-(3/4)) = 12/16. Therefore, the conditional PMF P X∣C (x) is given by:
P(X=3|C) = P(X=3 and C)/P(C) = (3/4)^2(1/4)/(12/16) = 1/3
P(X=4|C) = P(X=4 and C)/P(C) = (3/4)^3(1/4)/(12/16) = 1/4
...
(e) The conditional PMF P Y∣C (y) of Y given the event C={X>2} can be obtained by shifting the conditional PMF P X∣C (x) of X given the event C={X>2} by 2 units to the left. Therefore, P Y∣C (y) = P X∣C (y+2) for all y in support of Y. This conditional PMF belongs to the family of geometric random variables with parameter 1/4.
(f) The conditional mean E[X|C] can be calculated using the formula E[X|C] = sum(x*P(X=x|C)) for all x in the support of X. Since the conditional PMF P X∣C (x) is a geometric distribution with parameter 1/4 shifted by 2 units to the right, we can use the formula E[X|C] = 2 + 1/(1/4) = 6.
https://brainly.com/question/30144287
#SPJ1
Enter the number that belongs in the green box 7 4 8

Answers
Answer:
61.03°
Step-by-step explanation:
You want the angle opposite the side of length 7 in the triangle with other sides of lengths 4 and 8.
Law of CosinesThe law of cosines relates the angles of a triangle to the side lengths. For triangle ABC with opposite sides a, b, c, the relation is ...
c² = a² +b² -2ab·cos(C)
ApplicationSolving for angle C, we have ...
cos(C) = (a² +b² -c²)/(2ab)
C = arccos((a² +b² -c²)/(2ab))
In this triangle, that means ...
C = arccos((4² +8² -7²)/(2·4·8)) = arccos(31/64)
C ≈ 61.03°
The angle of interest is about 61.03°.
__
Additional comment
We get the same result from a triangle solver. See the second attachment. (The angle we want is angle B in that attachment.)
<95141404393>


A successful basketball player has a height of 6 feet 4 inches, or 193 cm. Based on statistics from a data set, his height converts to the z score of 2.66. How many standard deviations is his height above the mean?
Answers
Answer: 2.66 standard deviations above the mean
Explanation:
The z score directly determines how far we are from the mean. For positive z values, we are above the mean, while negative z values are below the mean.
The mean itself is z = 0
The absolute value of the z score is the distance from the score to 0. So having a z score of z = 2.66 means we are 2.66 standard deviations above the mean. Something like z = -2 means we are 2 standard deviations below the mean.
Write the equation of the line that passes through the points (3, -4) and (7, 6). Put
your answer in fully simplified point-slope form, unless it is a vertical or horizontal
line.
Answers
Answer:
Step-by-step explanation:
To write the equation of the line that passes through the points (3, -4) and (7, 6), we can follow these steps:
Step 1: Find the slope of the line
The slope of a line passing through two points (x1, y1) and (x2, y2) is given by:
slope = (y2 - y1) / (x2 - x1)
Plugging in the given values, we get:
slope = (6 - (-4)) / (7 - 3)
slope = 10 / 4
slope = 5 / 2
Step 2: Use point-slope form to write the equation of the line
Point-slope form of a line with slope m passing through a point (x1, y1) is given by:
y - y1 = m(x - x1)
We can use either of the given points to write the equation. Let's use (3, -4):
y - (-4) = (5/2)(x - 3)
Simplifying this equation, we get:
y + 4 = (5/2)x - (15/2)
Subtracting 4 from both sides, we get:
y = (5/2)x - (23/2)
This is the equation of the line in point-slope form.
Step 3: Simplify the equation if it is not in point-slope form
The equation we obtained in step 2 is already in point-slope form, so we do not need to simplify it any further.
Note: If the line was horizontal (i.e., it had zero slope), then its equation would be y = constant, where the constant is the y-coordinate of any point on the line. If the line was vertical (i.e., its slope was undefined), then its equation would be x = constant, where the constant is the x-coordinate of any point on the line.
A riddle for the day
I am less than 7 tens and more than 4 tens I am a odd number if you add both my digits you will get 11 which number am I?
47
65
67
74
Answers
Answer:
two of them are possible which one is the correct
100 POINTS TO ANYONE CORRECT + BRAINLIEST
On the day a smoothie cafe first opened, it had 140 customers. 65% of the customers ordered a large mango smoothie.
How many customers ordered a large mango smoothie?
Answers
Answer: 91
Step-by-step explanation: cross multiply.
A woman weighing 130 lbs drinks 2 mixed drinks (2 oz of liquor mixed with soda) with
dinner between 7-8 pm. At 10 pm she had a glass of wine.What was her BAC at 8 pm?
Answers
Answer:
Step-by-step explanation:
The BAC (Blood Alcohol Concentration) of a person depends on several factors, such as the amount of alcohol consumed, the time over which the alcohol was consumed, and the weight and gender of the person. For this problem, we will assume that the woman has a normal metabolism and that the alcohol is completely absorbed into her bloodstream.
To calculate the BAC at 8 pm, we need to know the amount of alcohol that the woman consumed and the time over which she consumed it. We are given that she had 2 mixed drinks between 7-8 pm, which contained a total of 2 ounces of liquor. We are also given that she had a glass of wine at 10 pm, but we don't need to consider this for the BAC at 8 pm.
Using the Widmark formula, we can calculate the BAC at 8 pm:
BAC = (Alcohol consumed / (Body weight x r)) - (0.015 x Hours since first drink)
where r is the gender constant (0.55 for females) and 0.015 is the rate at which the liver metabolizes alcohol.
Plugging in the values we know, we get:
BAC = (2 oz / (130 lbs x 0.55)) - (0.015 x 1 hour)
BAC = 0.0208 - 0.015
BAC = 0.0058
Therefore, the woman's BAC at 8 pm was approximately 0.0058, which is below the legal limit for driving in most states in the US.
The scatterplot above displays the relationship between the amount of food hippopotamuses eat per day and their age. Describe and explain any associations and data features on the scatterplot. Then, use the variables on the graph to interpret the relationship that is shown.

Answers
The scatter plot shows a [positive linear] association.
How to determine the association of the scatterplotFrom the question, we have the following parameters that can be used in our computation:
The image of the scatter plot
On the scatter plot, we can see that
The points appear to be on a straight line
Also, we can see that
As the x values increases the y values increases
This represents a positive linear association.
Hence, the association is a positive linear association.
Read more about scatter plot at
brainly.com/question/16920148
#SPJ1
Human blood is divided into 8 possible blood types. The rarest blood type is AB negative. Only 1% of the population has this blood type. Suppose a random sample of 50 people is selected. Can we find the probability that more than 3% of the sample has AB negative blood
Answers
Using the normal approximation to the binomial distribution, it is found since np = 0.5 < 10, we cannot find the probability.
Normal Probability DistributionIn a normal distribution with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X.The binomial distribution is the probability of x successes on n trials, with p probability of a success on each trial. It can be approximated to the normal distribution with \(\mu = np, \sigma = \sqrt{np(1-p)}\), as long as \(np \geq 10, n(1 - p) \geq 10\).In this problem, we have that:
Only 1% of the population has this blood type, hence p = 0.01.A random sample of 50 people is selected, hence n = 50.Then:
np = 50 x 0.01 = 0.5 < 10.
Thus we cannot find the probability.
More can be learned about the normal approximation to the binomial distribution at https://brainly.com/question/14424710
A manufacturer has 576 square inches of material available to construct the 6 faces of a carton, which will be in the shape of a rectangular prism. To maximize the volume, the carton will have dimensions such that the length and width are each twice the height.
Answers
To maximize the volume, of the rectangular prism, the carton should have dimensions of approximately 10.74 inches (length), 10.74 inches (width), and 5.37 inches (height).
What is the dimension required to maximize the volume of the box?Assuming the height of the rectangular prism is h inches.
According to the given information, the length and width of the prism will be twice the height, which means the length is 2h inches and the width is also 2h inches.
The total surface area of the rectangular prism is given by the formula:
Surface Area = 2lw + 2lh + 2wh
Substituting the values, we have:
576 = 2(2h)(2h) + 2(2h)(h) + 2(2h)(h)
576 = 8h² + 4h² + 4h²
576 = 16h² + 4h²
576 = 20²
h² = 576/20
h² = 28.8
h = √28.8
h = 5.37
The height of the prism is approximately 5.37 inches.
The length and width will be twice the height, so the length is approximately 2 * 5.37 = 10.74 inches, and the width is also approximately 2 * 5.37 = 10.74 inches.
Learn more on maximizing volume here;
https://brainly.com/question/10373132
#SPJ4
Please help I need this will give 100 points please help

Answers
The solution to the inequality f(x²-2) < f(7x-8) over D₁ = (-∞, 2) is:
-∞ < x < 1 or 1 < x < 6 or 6 < x < 2
Solving Inequality in a given domainGiven the inequality,
f(x²-2) < f(7x-8) over D₁ = (-∞, 2)
We need to find the values of x that satisfy this inequality.
Since we know that f is increasing over its domain, we can compare the values inside the function to determine the values of x that satisfy the inequality.
First, we can find the values of x that make the expressions inside the function equal:
x² - 2 = 7x - 8
Simplifying, we get:
x² - 7x + 6 = 0
Factoring, we get:
(x - 6)(x - 1) = 0
So the values of x that make the expressions inside the function equal are x = 6 and x = 1.
We can use these values to divide the domain (-∞, 2) into three intervals:
-∞ < x < 1, 1 < x < 6, and 6 < x < 2.
We can choose a test point in each interval and evaluate
f(x² - 2) and f(7x - 8) at that point. If f(x² - 2) < f(7x - 8) for that test point, then the inequality holds for that interval. Otherwise, it does not.
Let's choose -1, 3, and 7 as our test points.
When x = -1, we have:
f((-1)² - 2) = f(-1) < f(7(-1) - 8) = f(-15)
Since f is increasing, we know that f(-1) < f(-15), so the inequality holds for -∞ < x < 1.
When x = 3, we have:
f((3)² - 2) = f(7) < f(7(3) - 8) = f(13)
Since f is increasing, we know that f(7) < f(13), so the inequality holds for 1 < x < 6.
When x = 7, we have:
f((7)² - 2) = f(47) < f(7(7) - 8) = f(41)
Since f is increasing, we know that f(47) < f(41), so the inequality holds for 6 < x < 2.
Therefore, the solution to the inequality f(x²-2) < f(7x-8) over D₁ = (-∞, 2) is:
-∞ < x < 1 or 1 < x < 6 or 6 < x < 2
Learn more about inequality here:
https://brainly.com/question/25944814
#SPJ1
