Answers
2nd tan = 13 / 6
x = 65.22
to the nearest degree, it would be 65°.
Related Questions
1
A line passes through the point (-7, 5) and has a slope of 2. Which is another point that the line passes through?
O (-13, 9)
O (-9, 13)
O (9, 13)
O (13,9)

Answers
Answer:
D
Step-by-step explanation:
I would have to assume its D since the starting point is (-7, 5) and the slope is 1/2, since it is a positive slope it would reach (13, 9)
What is the x intercept of the line
A(0,2)
B(-7,0)
C(2,0)
D(0,-7)
PLZ I NEED THIS TO PASS MY CLASS
Btw the top is y the image was too long to fit

Answers
Help... It's homework, I need ur Help :""""")
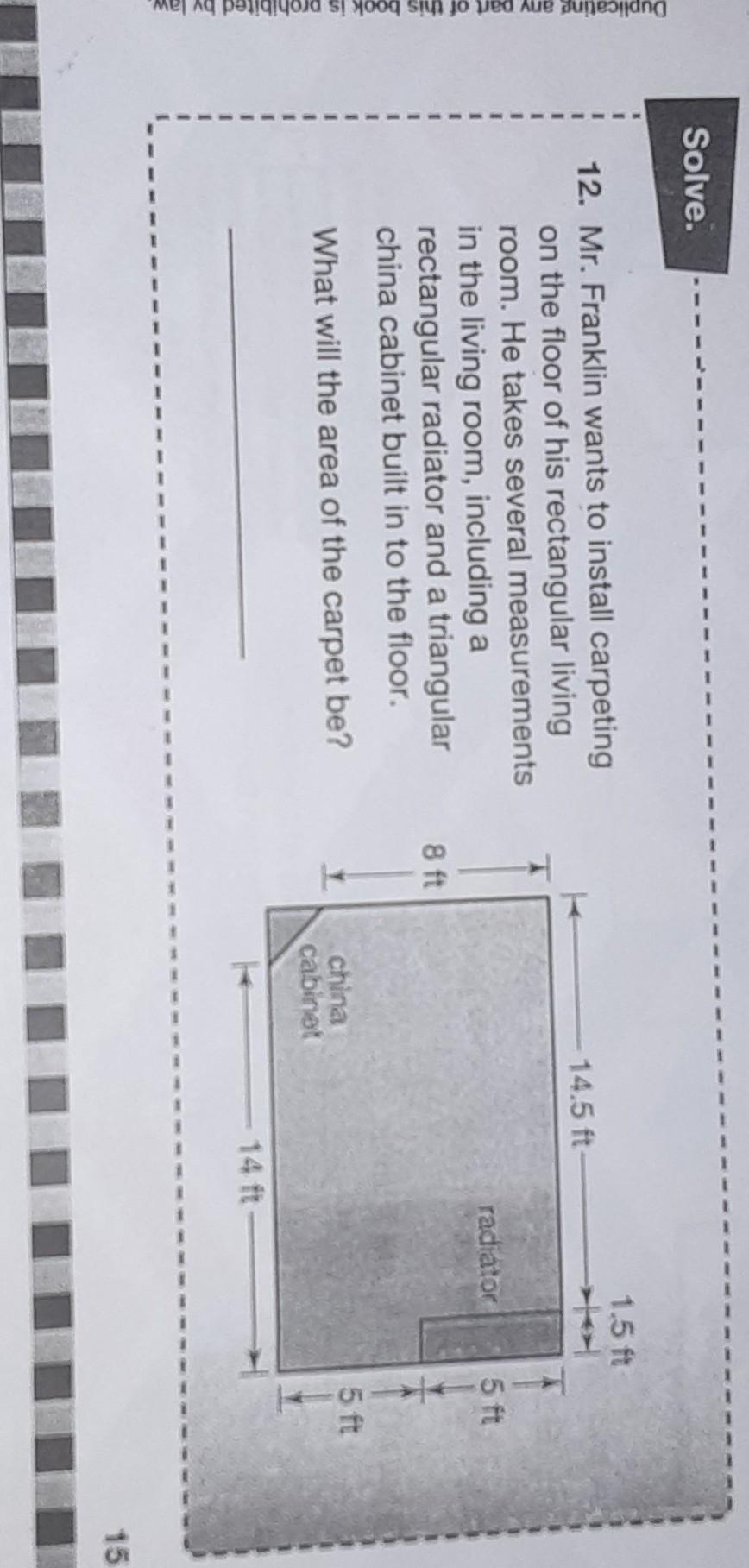
Answers
Answer:
112
Step-by-step explanation:
the formula for area is length times width,so in this case 14×8 = the area
Suppose f(x, y, z) = x2 + y2 + z2 and W is the solid cylinder with height 5 and base radius 6 that is centered about the z-axis with its base at z : -1. Enter O as theta. - (a) As an iterated integral, F sav = 10% x^2+y^2+z12 dz dr de W with limits of integration A = 0 B = C= 0 D= 6 E = -1 F = (b) Evaluate the integral.
Answers
∫_A^B ∫_B^C ∫_D^E (10%)(x^2 + y^2 + z^12) dz dr dθ.
This represents the full iterated integral for F_sav over the given solid cylinder.
(a) The iterated integral for F_sav with the given limits of integration is as follows:
∫∫∫_W (10%)(x^2 + y^2 + z^12) dz dr dθ,
where the limits of integration are A = 0, B = C = 0, D = 6, and E = -1.
(b) To evaluate the integral, we begin with the innermost integration with respect to z. Since z ranges from -1 to 6, the integral becomes:
∫∫_D^E (10%)(x^2 + y^2 + z^12) dz.
Next, we integrate with respect to r, where r represents the radial distance from the z-axis. As the solid cylinder is centered about the z-axis and has a base radius of 6, r ranges from 0 to 6. Thus, the integral becomes:
∫_B^C ∫_D^E (10%)(x^2 + y^2 + z^12) dz dr.
Finally, we integrate with respect to θ, where θ represents the angle around the z-axis. As the cylinder is symmetric about the z-axis, we integrate over a full circle, so θ ranges from 0 to 2π. Hence, the integral becomes:
∫_A^B ∫_B^C ∫_D^E (10%)(x^2 + y^2 + z^12) dz dr dθ.
This represents the full iterated integral for F_sav over the given solid cylinder.
The problem asks for the iterated integral of F_sav over the solid cylinder W. To evaluate this integral, we use the cylindrical coordinate system (r, θ, z) since the cylinder is centered about the z-axis. The function inside the integral is 10% times the sum of squares of x, y, and z^12. By integrating successively with respect to z, r, and θ, and setting appropriate limits of integration, we obtain the final iterated integral. The integration limits are determined based on the given dimensions of the cylinder.
Learn more about solid cylinder here:
https://brainly.com/question/30269341
#SPJ11
Given vectors a=(3, 2) and b=(-5, 6), find – 3a+2b.Write your answer in component form.-3a + 2b =
Answers
Vector a = (3, 2), then;
\(-3a=-3(3,2)\text{ = (-9,-6)}\)Also, vector b = (-5, 6), then;
\(2b=2(-5,6)=(-10,12)\)Then, -3a + 2b = (-9, -6) + (-10, 12)
\(\begin{gathered} -3a+2b=(-9+(-10),-6+12)_{} \\ -3a+2b=(-19,6) \end{gathered}\)The answer is (-19,6)
solve the inequality write the solution in interval notation
-x/3 < 5
Answers
The inequality expression given as -x/3 < 5 has a solution of x > -15
How to solve the inequality?From the question, the inequality is given as
-x/3 < 5
The above inequality can be re-written as follows
-x/3 < 5
There is no constant to add or subtract in the expression
So, we start by multiplying both sides of the expression by a constant
Multiply both sides by 3
expression
-x < 15
Divide both sides by -1
So, we have the following representation
x > -15
Hence, the solution to the expression is x > -15
Read more about inequality at
brainly.com/question/25275758
#SPJ1
Solve the LP problem using the simplex tableau method a) Write the problem in equation form (add slack variables) b) Solve the problem using the simplex method Max Z = 3x1 + 2x2 + x3 St 3x - 3x2 + 2x3 < 3 - X1 + 2x2 + x3 = 6 X1, X2,X3 20
Answers
A. x1, x2, x3, s1, s2 ≥ 0
B. New table au:
x1 x2 x3 s1 s2 RHS
x2 | 0 1 4/7 3/14 -1/14 1/2
s2 | 1 0 3/7 -1/14 3/14 3/2
Z | 0
a) Writing the problem in equation form and adding slack variables:
Maximize Z = 3x1 + 2x2 + x3
Subject to:
3x1 - 3x2 + 2x3 + s1 = 3
-x1 + 2x2 + x3 + s2 = 6
x1, x2, x3, s1, s2 ≥ 0
b) Solving the problem using the simplex method:
Step 1: Convert the problem into canonical form (standard form):
Maximize Z = 3x1 + 2x2 + x3 + 0s1 + 0s2
Subject to:
3x1 - 3x2 + 2x3 + s1 = 3
-x1 + 2x2 + x3 + s2 = 6
x1, x2, x3, s1, s2 ≥ 0
Step 2: Create the initial tableau:
x1 x2 x3 s1 s2 RHS
s1 | 3 -3 2 1 0 3
s2 | -1 2 1 0 1 6
Z | 3 2 1 0 0 0
Step 3: Perform the simplex method iterations:
Iteration 1:
Pivot column: x1 (lowest ratio = 3/1 = 3)
Pivot row: s2 (lowest ratio = 6/2 = 3)
Perform row operations to make the pivot element equal to 1 and other elements in the pivot column equal to 0:
s2 = -s2/3
x2 = x2 + (2/3)s2
x3 = x3 - (1/3)s2
s1 = s1 - (1/3)s2
Z = Z - (3/3)s2
New tableau:
x1 x2 x3 s1 s2 RHS
x1 | 1 -2/3 -1/3 0 1/3 2
s2 | 0 7/3 4/3 1 -1/3 2
Z | 0 2/3 2/3 0 -1/3 2
Iteration 2:
Pivot column: x2 (lowest ratio = 2/7)
Pivot row: x1 (lowest ratio = 2/(-2/3) = -3)
Perform row operations to make the pivot element equal to 1 and other elements in the pivot column equal to 0:
x1 = -3x1/2
x2 = x2/2 + (1/7)x1
x3 = x3/2 + (4/7)x1
s1 = s1/2 - (1/7)x1
Z = Z/2 - (2/7)x1
New tableau:
x1 x2 x3 s1 s2 RHS
x2 | 0 1 4/7 3/14 -1/14 1/2
s2 | 1 0 3/7 -1/14 3/14 3/2
Z | 0
Learn more about table from
https://brainly.com/question/30801679
#SPJ11
What is the inverse of the function f(x) = 2x - 10?
Answers
Simplify: (13/11)x(-14/5)+(13/11)x(-7/5)+(-13/11)x(34/5)
Thankyou
Answers
Answer:
In this I have answered this problem.

1. Write a multiplication expression that you can use
to find 16 ÷ 4/5
Answers
Multiplication expression used is 16 ×\(\frac{5}{4}\).
What is multiplicative inverse?A number that when multiplied by a number x results in the multiplicative identity, 1, is known as a multiplicative inverse or reciprocal, indicated by 1/x or x1. A fraction a/b has a multiplicative inverse of b/a. Divide 1 by the real number to obtain the multiplicative inverse of the number. When a number is multiplied by its original number, the multiplicative inverse of that number, or x-1, produces a value equal to 1. The multiplicative inverse of 2, for instance, is 2-1 since it fulfils the formula: 2 x 2-1
2 x \(\frac{1}{2}\)= 1. It is also known as a number's reciprocal.
Given Data
16 ÷ \(\frac{4}{5}\)
Reciprocating,
16 × \(\frac{5}{4}\)
Simplifying,
4(5)
20
Multiplication expression used is 16 ×\(\frac{5}{4}\)
To learn more about multiplicative inverse, visit:
https://brainly.com/question/13715269
#SPJ9
URGENT! Please help
What is the value of 7 for the following data to three decimal places?
A. 0.852
B. 0.930
C. 0.659
D. 0.964

Answers
Answer:
Option B
Step-by-step explanation:
Given that two variables in the table as
Total Average
x 2 6 7 8 12 35 7
y 15 13 9 8 5 50 10
xy 30 78 63 64 60 295 59
(x-7)^2 25 1 0 1 25 52 10.4
(y-10)^2 25 9 1 4 25 64 12.8
Var x = 10.4 and std dev x = 3.225
Var Y = 12.8 and std dev Y = 3.578
Cov (xy) = E(xy)-E(x) E(Y)=59-70=-11
Correlation coefficient r
= Cov /sx sy = -11/(3.225)(3.578)=-0.9532
Round off to get
r=-0.953
Henceoption B is right.
I hope my answer helped! <3
Solve the following systems of inequalities and select the correct graph: 2x − y > 4 x + y < −1 In each graph, the area for f(x) is shaded and labeled A, the area for g(x) is shaded and labeled B, and the area where they have shading in common is labeled AB. What graph would I be using?
Answers
9514 1404 393
Answer:
see below
Step-by-step explanation:
The "solution" is the doubly-shaded area on the graph. Here, the dashed lines cross in a sort of X pattern, and the doubly-shaded area is the quadrant at the bottom (below both lines).
__
The "solution" involves graphing the boundary lines, and identifying the shaded area associated with each.
When equations are in standard form, there are a couple of different ways you can graph them. (I like to use a graphing calculator.) One way is to rewrite the equations to slope-intercept form:
y < 2x -4 . . . . . . slope of 2, y-intercept of -4, shading below the dashed line
y < -x -1 . . . . . . . slope of -1, y-intercept of -1, shading below the dashed line
__
Comment on multiple choice questions
You need to identify what makes each answer choice different from the others. It might be the slopes of the lines, the y-intercepts, the side that is shaded, the nature of the line (dashed, solid). You can usually eliminate the answer choices that don't make any sense, and concentrate on the subtleties of the remaining viable candidates.

The "solution" is the doubly-shaded area on the graph. Here, the dashed lines cross in a sort of X pattern, and the doubly-shaded area is the quadrant at the bottom (below both lines).
What is a graph?A graph is the representation of the data on the vertical and horizontal coordinates so we can see the trend of the data.
The "solution" involves graphing the boundary lines and identifying the shaded area associated with each.
When equations are in standard form, there are a couple of different ways you can graph them. (I like to use a graphing calculator.) One way is to rewrite the equations to slope-intercept form:
y < 2x -4 . . . . . . slope of 2, y-intercept of -4, shading below the dashed line
y < -x -1 . . . . . . . slope of -1, y-intercept of -1, shading below the dashed line
Therefore "solution" is the doubly-shaded area on the graph. Here, the dashed lines cross in a sort of X pattern, and the doubly-shaded area is the quadrant at the bottom (below both lines).
To know more about graphs follow
https://brainly.com/question/25020119
#SPJ2

WILL GIVE BRIANLIEST!!!!!!!!!!!!!!!!!!!!! picture down below ↓↓↓↓↓↓

Answers
Answer:
C
Step-by-step explanation:
A and c are parallel
B and d are parallel
A and c are intersecting
Plssssssssssssssss help

Answers
Answer:
EF is the chord of K
hope it helped
Answer:
EF is the chord of K
Step-by-step explanation:
plz mark me as brainliest
Write an equivalent equation to AB = AC using A^-1 such that, when it is simplified, the resulting equation will simplify to B = C. What property should be used to continue simplifying the above equation? A. (AB)^-1 = B^-1A^-1 B. (A^-1)^T = (A^T)^-1 C. A-^1A = 1 D. (A^-1)^-1 = A
Answers
The property that should be used to continue simplifying the above equation is A-^1A = 1. So, correct option is C.
We can start with the equation AB = AC and multiply both sides by A^-1 on the left:
A^-1(AB) = A^-1(AC)
Using the associative property of matrix multiplication, we can simplify the left-hand side:
(A^-1A)B = (A^-1A)C
Using the fact that A^-1A = I (the identity matrix), we get:
IB = IC
Simplifying further using the fact that I times any matrix is that matrix itself, we obtain:
B = C
Therefore, the equivalent equation to AB = AC using A^-1 that simplifies to B = C is A^-1(AB) = A^-1(AC), and the property used to continue simplifying the equation is A^-1A = I.
The correct option is (C) A^-1A = 1, which is equivalent to A^-1A = I, since the identity matrix is denoted as 1 in some contexts.
To learn more about equation click on,
https://brainly.com/question/30673951
#SPJ4
Which two of the following are not characteristics of surveys?
A. Data are gathered during the course of the study.
B. Two or more treatments are compared imthe study.
C. The results of the study are analyzed statistically.
D. One or more treatment groups and a control group are included in
the study
Answers
Answer:
B and D
Step-by-step explanation:
Surveys are only tested with one group.
what is the measure of angle b?
A. 36⁰
B. 117⁰
C.63⁰
D. 56⁰

Answers
Answer:
A
Step-by-step explanation:
180⁰= a+b+81⁰
a=180⁰-117⁰=63⁰
b=180⁰-63⁰-81⁰=36⁰
find dy/dx. x = t sin(t), y = t2 + 8t
Answers
find dy/dx
x= t sin(t); (Given in the question)
y= t²+8t; (Given in the question)
then, x= t sin(t)
dx/dt = sin t + t cos t ;
y= t²+8t
dy/dt = 2t + 8;
then, dy/dx = dy/dt x dx/dt
dy/dx = (2t+8)/(sin t + t cos t)
dy/dx = 2(t+4)/(sin t + t cos t)
Learn more about derivative at:
brainly.com/question/23847661
#SPJ4
What fraction is equivalent to 150%?
A. 1 2/5
B. 15/1
C. 3/5
D. 1 1/2
Answers
Answer:
D : 1 1/2
Step-by-step explanation:
150% converted into a decimal is 1.5, this is the same as 1 1/2, so the answer is D.
hope this helps :)
The 150% as a fraction in simplest form is D. 1 1/2
What is the fundamental principle of multiplication?Multiplication is the mathematical operation that is used to determine the product of two or more numbers. If an event can occur in m different ways and if following it, a second event can occur in n different ways, then the two events in succession can occur in m × n different ways.
We have to write 150% as a fraction in simplest form.
So we put 150 over 100
That is (150/100)
Now multiply the top and the bottom by 10 to get rid of the decimal as;
15/10
1.5 = 1 1/2
Hence, the fraction in simplest form is 1 1/2
Learn more about multiplications;
brainly.com/question/14059007
#SPJ2
Can you guys help me with these questions?


Answers
Answer:
13. 23 boat rides; 22 are full, and the first one has 301 passengers.
12. $11,067.50
Write a proportion for each set of similar polygons. Solve for the unknown side.
Type the FULL Answer for both questions.
Pls Answer!


Answers
Step-by-step explanation:
The proportion of similar triangles are
\( \frac{3}{4} = \frac{9}{r} \)
Solving for r
\( \frac{4}{3} = \frac{r}{9} \)
\( \frac{9 \times 4}{3} = r\)
\(12 = r\)
PLZ HELP!!! I'm begging you! Problem: If each letter of the alphabet is worth two more numbers than the number before it (1=1, 2=3), what is the entire alphabet worth?
Answers
Answer:
676
Step-by-step explanation:
I think this is an arithmetic series, so
Sn = 26/2[2(1) + (26 - 1)2]
Sn = 13[2 + 50]
Sn = 13[52]
Sn = 676
Answer:
676
Step-by-step explanation:
A = 1
B = 3
C = 5
D = 7
...
Z = 51
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25
(+) + 51 + 49 + 47 + 45 + 43 + 41 + 39 + 37 + 35 + 33 + 31 + 29 + 27
---------------------------------------------------------------------------------------------------
52 + 52 + 52 + 52 + 52 + 52 + 52 + 52 + 52 + 52 + 52 + 52 + 52
13 * 52 = 676
Answer: 676
Mae Ling earns a weekly salary of $320 plus a 6. 0% commission on sales at a gift shop. How much would she make in a work week if she sold $4,500 worth of merchandise?
Answers
Mae Ling make $590 in a work week if she sold $4,500 worth of merchandise.
The given is:
We need to find how much she would earns in a work week
Mae Ling earns a weekly salary of $320
She earns a 6.0% commission on sales
She sold by $4,500 in that week
Add $320 to the product of 6.0% and $4,500
She made = 320 + (6.0% × 4,500)
6.0% = 6.0 ÷ 100 = 0.06
She made = 320 + (0.06 × 4,500)
She made = 320 + 270
She made = 590
She would make $590 in a work if she sold $4,500 worth of merchandise.
To know more about commission
https://brainly.com/question/19298781
#SPJ4
We are interested in determining whether or not the following linear matrix equation is ill-conditioned, AO=b, where A ER", ER" and b ER". In order to do this, we calculate the conditioning number of A, denoted by K,(A). a 0 0 Suppose it was found that k, (A)=5 and A=0 1 0 where a € (0,1). What is the value of a? Give your answer to three decimal places.
Answers
The condition number of a matrix A is defined as the product of the norm of A and the norm of the inverse of A, divided by the norm of the identity matrix. That is:
K(A) = ||A|| ||A^(-1)|| / ||I||
If K(A) is large, it means that small changes in the input to the matrix equation can cause large changes in the output, indicating that the problem is ill-conditioned.
In this case, we are given that K(A) = 5, and that A is a 2x2 matrix with entries a, 1, 0, and 0. That is:
A = [a 1; 0 0]
To find the value of a, we need to use the definition of the condition number and some properties of matrix norms. We have:
||A|| = max{||Ax|| / ||x|| : x != 0}
Since A is a 2x2 matrix, we can compute the norm using the formula:
||A|| = sqrt(max{eigenvalues of A^T A})
The eigenvalues of A^T A are a^2 and 1, so:
||A|| = sqrt(a^2 + 1)
Similarly, we have:
||A^(-1)|| = sqrt(max{eigenvalues of A^(-1) A^(-T)})
Since A is a diagonal matrix, its inverse is also diagonal, with entries 1/a, 0, 0, and 1. Therefore:
A^(-1) A^(-T) = [(1/a)^2 0; 0 0]
The eigenvalues of this matrix are (1/a)^2 and 0, so:
||A^(-1)|| = sqrt((1/a)^2) = 1/|a|
Finally, we have:
||I|| = max{||Ix|| / ||x|| : x != 0} = 1
Putting it all together, we get:
K(A) = ||A|| ||A^(-1)|| / ||I|| = (sqrt(a^2 + 1) / |a|) / 1 = sqrt(a^2 + 1) / |a| = 5
Squaring both sides and rearranging, we get:
a^2 + 1 = 25a^2
24a^2 = 1
a^2 = 1/24
a = ±sqrt(1/24) = ±0.204
Since a is required to be in the interval (0, 1), the only valid solution is a = 0.204 (rounded to three decimal places).
Learn more about identity matrix here:
https://brainly.com/question/11335369
#SPJ11
Enter the correct answer in the box. Write your answer in the form y = mx + b, using the appropriate inequality symbol in place of the equal sign.
helpp

Answers
The graph as an inequality expression is y < -2x - 3
Representing the graph as an inequalityFrom the question, we have the following parameters that can be used in our computation:
The graph of the inequality
A linear equation is represented as
y = mx + c
Where
c = y when x = 0
So, we have
c = -3 from the graph
The equation becomes
y = mx - 3
Using the other points, we have
-3m - 3 = 3
So, we have
-3m = 6
This gives
m = -2
Recall that
y = mx - 3
So, we have
y = -2x - 3
The bottom part is the shaded region
So, we have
y < -2x - 3
Hence, the graph as an inequality is y < -2x - 3
Read more about inequality at
https://brainly.com/question/30390162
#SPJ1
BBQ Corp. had a 3:1 stock split ratio. Pre-split the company had 1.35 Million outstanding shares at a price of $72.45 per share.
What is the price per share of BBQ Corp. stock post-split?
Answers
The price per share of BBQ Corp. after there has been a stock split, or post - split, is $24. 15
How to find the price after a stock split?When there is a stock - split, then each of outstanding shares that a company has, is divided into a number of shares that is determined by the stock split ratio.
The price of the individual shares are also divided into the same ratio as the shares.
This means that the price per share for BBQ Corp. post - split is:
= Price per share before split / 3
= 72. 45 / 3
= $24. 15
Find out more on stock - splits at https://brainly.com/question/25300299
#SPJ1
In the exponential ab = c the answer is no solution when:
c-is a fraction
b-is negative
c-is negative
o a is a fraction
a is positive
b-is a fraction
c-is zero
Answers
In the exponential ab = c, there are certain conditions where there is no solution. Firstly, if c is negative, there is no solution because there is no real number that can be raised to any power to give a negative result.
Secondly, if b is negative and c is a fraction, there is no solution because the result of raising a negative number to a fractional power is not a real number. Thirdly, if a is a fraction and c is zero, there is no solution because any number raised to the power of zero is equal to one, and there is no fraction that can be equal to one. Lastly, if a is positive and b is a fraction, there is no solution because any number raised to a fractional power will always give a positive result. Therefore, these are the conditions where there is no solution in the exponential ab = c equation.
To know more about Exponential visit :
https://brainly.com/question/29160729
#SPJ11
How do you eliminate the parameter to find a cartesian equation of the curve?
Answers
A horizontal parabola with a right-facing opening and a vertex at (1,1) is we have positive direction.
In order to make the coefficients of either the variable x or the variable y numerically equal, first multiply both of the following equations by any suitable non-zero constants.
Finding the single equation of a curve in standard form with only the variables xs and ys constitutes the cartesian equation of that curve. You must simultaneously solve the parametric equations in order to arrive to this equation.
X and Y both
are t-related functions.
We have t=y1 after solving y=t+1 to get t as a function of y.
Thus, given x=t2+1, we have x=(y1)2+1x1=(y1) by substituting t=(y1).
A horizontal parabola with a right-facing opening and a vertex at (1,1) is what we have positive direction.
To learn more about cartesian equation :
https://brainly.com/question/7291171
#SPJ4
A test used to determine whether or not first-order autocorrelation is present is _____ test.
a. chi-square
b. t
c. Durbin-Watson
d. serial-autocorrelation
Answers
The test used to determine whether or not first-order autocorrelation is present is the Durbin-Watson test.
1. Fit a regression model to the data.
2. Obtain the residuals, which represent the differences between the observed values and the predicted values from the regression model.
3. Calculate the Durbin-Watson statistic, which is a ratio of the sum of squared differences between adjacent residuals to the sum of squared residuals.
4. Compare the calculated Durbin-Watson statistic to critical values from a Durbin-Watson table or use statistical software to determine if there is significant autocorrelation.
5. The Durbin-Watson statistic ranges from 0 to 4, where a value around 2 suggests no autocorrelation, a value below 2 indicates positive autocorrelation, and a value above 2 indicates negative autocorrelation.
6. By analyzing the Durbin-Watson statistic, researchers can make conclusions about the presence or absence of first-order autocorrelation in the regression model.
Learn more about sum : brainly.com/question/31538098
#SPJ11
A company expands and hires some new employees. If the ratio of new employees to old employees in the company is 1 : 3, and there are now 1,200 people working for the company, how many new employees did the company hire?
Answers
Answer:
300 new employees
Step-by-step explanation:
1:3
x + 3x = 1,200
4x = 1200
x = 300
