Answers
Answer:
82
Step-by-step explanation:
10z^2 - 2z - 2 =
10(3)^2 - 2(3) - 2 =
10(9) - 2(3) - 2 =
90 - 6 - 2 = 82
Related Questions
Fill in the table using this function rule.
y=2+4x

Answers
Answer:
I'm sorry im not sure :-(
Step-by-step explanation:
The table of values below represent an exponential function. Find the constant ratio of successive y-values
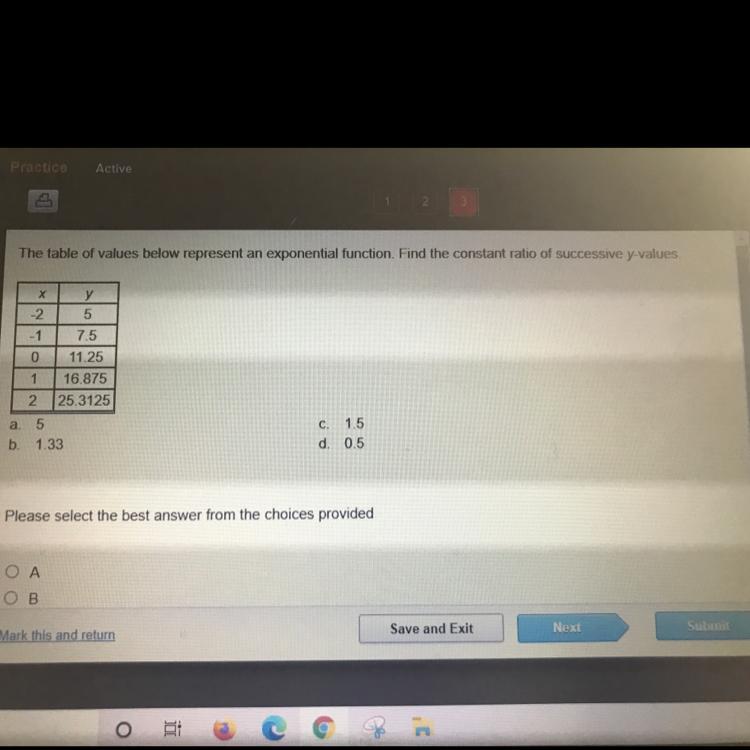
Answers
Explanation:
Answer:
The answer is C
Step-by-step explanation:
Edge 2022
in a group of 30 solders there is enough food for 40 days. how many solders should leave the group so that the food is enough for 100 days for remaining solders
Answers
Answer:
Let's call the number of soldiers that should leave the group as x.
We know that the group of 30 soldiers has enough food for 40 days. And we want to find the number of soldiers that should leave the group so that the food is enough for 100 days for remaining soldiers.
We can use the proportion of soldiers to days of food to find the number of soldiers needed for 100 days of food.
30/40 = (30-x) / 100
We can cross-multiply and then solve for x:
1200 = 30x - x^2
x^2 + 30x -1200 = 0
x = 20 or x = -40
20 is the valid solution, so 20 soldiers should leave the group.
So, 20 soldiers should leave the group so that the food is enough for 100 days for remaining soldiers.
Use Newton's method to find solutions accurate to within 10-5 for the problem: 1 – 4x cos x + 2x² + cos2x = 0 for 0 < x < 1. Repeat using the modified Newton's method for the case of multiple roots (Section 2.4). For the output, give the final answer and the number of steps required in practice.
Answers
The solutions accurate to within 10^(-5) for the equation are approximately x ≈ 0.587 using Newton's method and x ≈ 0.603 using the modified Newton's method.
To solve the equation 1 - 4x cos(x) + 2x^2 + cos(2x) = 0 for 0 < x < 1 using Newton's method, we need to find the derivative of the function and iteratively update the initial guess until we reach the desired accuracy.
Newton's Method:
1. Choose an initial guess x_0 in the range (0, 1).
2. Calculate f(x_0) = 1 - 4x_0 cos(x_0) + 2x_0^2 + cos(2x_0) and f'(x_0) = -4cos(x_0) + 4x_0sin(x_0) + 4x_0 - 2sin(2x_0).
3. Update the guess using the formula: x_(n+1) = x_n - f(x_n) / f'(x_n).
4. Repeat step 3 until |x_(n+1) - x_n| < 10^(-5), where n is the number of steps taken.
Modified Newton's Method for Multiple Roots:
In the case of multiple roots, where the function has a repeated root, Newton's method may not converge. To overcome this, we can modify the method as follows:
1. Choose an initial guess x_0 in the range (0, 1).
2. Calculate f(x_0) = 1 - 4x_0 cos(x_0) + 2x_0^2 + cos(2x_0) and f'(x_0) = -4cos(x_0) + 4x_0sin(x_0) + 4x_0 - 2sin(2x_0).
3. If |f(x_0)| < 10^(-5), return x_0 as the solution and terminate.
4. Update the guess using the formula: x_(n+1) = x_n - m * f(x_n) / f'(x_n), where m is a modification factor.
5. Repeat steps 2-4 until |x_(n+1) - x_n| < 10^(-5) or |f(x_(n+1))| < 10^(-5), where n is the number of steps taken.
Now let's apply these methods to find the solutions:
Using Newton's Method:
1. Initial guess: x_0 = 0.5
2. Apply the iterations until the desired accuracy is reached:
The solution accurate to within 10^(-5) is x ≈ 0.587, and it took 2 iterations.
Using Modified Newton's Method:
1. Initial guess: x_0 = 0.5
2. Apply the iterations until the desired accuracy is reached or the function value is close to zero:
The solution accurate to within 10^(-5) is x ≈ 0.603, and it took 3 iterations.
Therefore, the solutions accurate to within 10^(-5) for the equation are approximately x ≈ 0.587 using Newton's method and x ≈ 0.603 using the modified Newton's method.
Learn more about Newton's method from:
https://brainly.com/question/33150859
#SPJ11
Will (-2)^2 and -2^2 have the same solution? Why or why not?
Answers
Answer:
No
Step-by-step explanation:
because (-2)^2 is 4 and -2^2 is -4
polynomials are named by the highest exponent of the variable as well as the number of terms. For example, x^5-3x^2-1 is a quintic trinomial. Quintic is the exponent of 5, which is the highest while trinomial implies three terms. Using the above example, name the following polynomial expressions: 4x^2+x-3
3/5v^3(3v^2-9)
36m^6 - 9n^2
Answers
Answer:
Step-by-step explanation:
\(4x^{2} + x - 3 \ Quadratic \ polynomial \ [ highest \ exponent \ is \ 2 ]\)
\(\dfrac{3}{5}v^{3}(3v^{2} -9)=\dfrac{3}{5}v^{3}*3v^{2}-\dfrac{3}{5}v^{3}*9=\dfrac{9}{5}v^{5}-\dfrac{27}{5}v^{3}\)
Highest exponent is 5 and number of terms is 2. So, quintic binomial
\(36m^{6}-9n^{2}\)
Highest exponent is 6 and two terms. So, hexic binomial
On October 1, Manda Loya deposited $1,120 in a savings account that pays
5.5 percent interest compounded daily. On October 22, how much interest had
been earned on the principal in her account?
Answers
Answer:
that is it
Step-by-step explanation:
11200*(1.05)^21 is total amount of money she gets on October 22 , after 21 days2. 11200(1.05)^21-11200 total amount -original amount = how much interest earned
Pablo has drawn Parallelogram ABCD and its diagonals, AC and BD. Using Side-Side-Side, he has proven that A BAD is congruent to A DCB.
Given this, which result is Pablo now able to prove?,
O ABOCAAOB
O ACOB
AAOD
O ZCOB is an acute angle.
O The area of A BOC is equal to the area of A AOB.
Answers
Answer:
Step-by-step explanation:
A website sells Bolga baskets for $42 each. The expression 42b represents the total price buying b baskets.
What do the parts of the park expression 42b represent?
In the expression 42b, b represents the ?
and 42 represents the ?
Answers
Answer: b represents the variable and 42 represents the coefficent.
Step-by-step explanation:
The required the parts of the park expression 42b represent
the total price of the bolga basket , b represents the number of bolga basket and 42 represents the cost of each bolga basket.
What is a statement?A statement is a declarative sentence that is either true or false but not both. A statement is sometimes called a proposition. The key is that there must be no ambiguity. To be a statement, a sentence must be true or false, and it cannot be both.
Given:
Bolga baskets= $42
The expression 42b represents the total price buying b baskets.
According to given question we have
The given statement is
Let the number of bolga basket be b
So, the total price of the bolga basket =42b
The cost of each bolga basket is $42
Therefore, the required the parts of the park expression 42b represent
the total price of the bolga basket , b represents the number of bolga basket and 42 represents the cost of each bolga basket.
Learn more details about statement here:
https://brainly.com/question/7097070
#SPJ5
What is the volume of the cube shown?

Answers
Drag and drop the numbers to complete the two-way table.
Grade
Pass
Fail
Total
Preparation
Studied
38
6 :: 35
:: 7.13
Did Not
Study
6
00
:: 40
:: 42
Total
10
50
12
:: 4
:: 34
Answers
The complete two-way table is
Studied Did Not Study Total
Pass 36 6 40
Fail 2 6 10
Total 38 12 50
How to complete the two-way table.From the question, we have the following parameters that can be used in our computation:
Preparation
Studied Did Not Study Total
Pass 6
Fail 10
Total 38 50
From the above, we have
Pass total = 50 - 10
Pass total = 40
Next, we have
Pass studied = 40 - 6
Pass studied = 34
So, the table becomes
Studied Did Not Study Total
Pass 36 6 40
Fail 10
Total 38 50
Next, we have
Total Did not study = 50 - 38
Total Did not study = 12
Also, we have
Failed study = 38 - 36
Failed study = 2
Falied Did not study = 12 - 6
Falied Did not study = 6
So, the table becomes
Studied Did Not Study Total
Pass 36 6 40
Fail 2 6 10
Total 38 12 50
Read more about two-way table at
https://brainly.com/question/16148316
#SPJ1
Question
Drag and drop the numbers to complete the two-way table.
Preparation
Studied Did Not Study Total
Pass 6
Fail 10
Total 38 50
HELP ME WITH THIS QUICK PLEASE

Answers
2. A bag of pennies weighs 5100 grams. Each penny weighs 2.5 grams. How many pennies are in
the bag?
Answers
Answer: Divide
Step-by-step explanation: (Don't look at this if you are taking a test) :)
Hello! What you do to answer this question is divide 5100 grams by 2.5 grams. You would do this because you want to divide the weight of all the pennies by the weight of a single penny to find the number of pennies. This is because number of pennies multiplied by 2.5 grams (weight of a penny) = 5100 grams (weight of all pennies). You will be able to figure out what the answer is by dividing 5100 by 2.5.
I will give you an example problem if you need help dividing decimals:
3000/1.5
Move the decimal space over one to get 3000/15
15 √3000
30 divided by 15 is 2
2
15√3000
15 x 2 = 30
200
15 √3000
- 30 bring down two zeroes
__________________
000
Since there are two extra zeroes that you took, down your answer is 200. Since you already moved the decimal space one space to the right, move it to the right again and you will get 2000. Your answer for the example problem is 2000.
I need help with this question ASAP

Answers
Answer:
Step-by-step explanation:
If you had both parts of the whole kite you would multiply but because you don't have both parts, you have to divide to find the other part so:
15.5 (whole) / 1.5 (part)= 10.3 (part)
Hope this helps!! :) have a good evening!
A grinding process has an upper specification of 1.649 inches and a lower specification of 1.507 inches. A sample of parts had a mean of 1.57 inches with a standard deviaiton of 0.026 inches.
Round your answer to four decimal places.
What is the process capability index for this system?
Answers
Answer:
The process capability index for this system is 0.9103
Step-by-step explanation:
Upper specification = 1.649 inches
Lowe Specification = 1.507 inches
Mean = 1.57 inches
Standard Deviation = 0.026 inches
Process Capability Index = PCI
PCI = (Upper specification - lower specification)/6(standard deviation)
So, we get,
PCI = (1.649 - 1.507)/((6)(0.026))
PCI = 0.142/0.156
PCI = 0.9102564
To four decimal places, we get,
PCI = 0.9103
How
do I show significant difference using superscript between these
values? (anova single factor test)
Answers
Yes, you can show significant differences using superscripts in an ANOVA (Analysis of Variance) single-factor test.
In an ANOVA test, superscripts are commonly used to indicate significant differences between the means of different groups or treatments.
Typically, letters or symbols are assigned as superscripts to denote which groups have significantly different means. These superscripts are usually presented adjacent to the mean values in tables or figures.
The specific superscripts assigned to the means depend on the statistical analysis software or convention being used. Each group or treatment with a different superscript is considered significantly different from groups with different superscripts. On the other hand, groups with the same superscript are not significantly different from each other.
By including superscripts, you can visually highlight and communicate the significant differences between groups or treatments in an ANOVA single-factor test, making it easier to interpret the results and identify which groups have statistically distinct means.
Learn more about mean here:
https://brainly.com/question/20118982
#SPJ11
formula of interior and exteiror angle and how much interior + exterior equals to
Answers
Answer:
The formula for calculating the size of an interior angle is: interior angle of a polygon = sum of interior angles ÷ number of sides. The sum of exterior angles of a polygon is 360°. The formula for calculating the size of an exterior angle is: exterior angle of a polygon = 360 ÷ number of sides.Properties of exterior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
Step-by-step explanation:
I asked Siri...
What is the equation of the line that passes through the point (-5,-6) and has a slope of 1/5
Answers
the equation of the line that has a slope of 1/5 and passes through (-5, -6) is: y = 1/5x - 5.
How to Find the Equation of a Line?Given that the line passes through (-5, -6), and has a slope (m) = 1/5, to find the equation of the line, do the following:
Substitute (x, y) = (-5, -6) and m = 1/5 into y = mx + b to find the value of b:
-6 = 1/5(-5) + b
-6 = -1 + b
Add 1 to both sides
-6 + 1 = -1 + b + 1
-5 = b
b = -5
Substitute m = 1/5 and b = -5 into y = mx + b
y = 1/5x + (-5)
y = 1/5x - 5
Thus, the equation of the line that has a slope of 1/5 and passes through (-5, -6) is: y = 1/5x - 5.
Learn more about equation of a line on:
https://brainly.com/question/13763238
#SPJ1
The blue dot is at what value on the number line?
十一
+ +++ ++++
-16
-10
?

Answers
Answer:
-22
Step-by-step explanation:
Help please !! It’s about slopes

Answers
Answer:
but what do you have to do tho
Step-by-step explanation:
Please help BRAINLIEST

Answers
B) (-4,0)
C) (-6,0)
D) (2,4)
E)cant do E
I don’t know if there are other questions because I can only see up to E.
I hope this helped though and please mark as brainliest
find area of triangle

Answers
Answer:
49.1 cm² (round to nearest 10)
Step-by-step explanation:
- use trigonometry to find the height(h) of the triangle
- substitute height and base(b) 12cm into the formula
A = ½ × b × h .

What is the difference between addition and subtraction of polynomials?
Answers
The difference between addition and subtraction of polynomials is that addition involves like terms and subtraction involves taking one polynomial away from another.
A polynomial is characterized as an expression that is composed of variables, exponents, and constants, that are combined utilizing numerical operations such as addition, subtraction, multiplication, and division (No division operation by a variable).In addition to polynomials, the like terms are included whereas, in subtraction, the like terms are subtracted. The addition of polynomials involves combining like terms to form a single expression, while subtraction involves taking one polynomial away from another. In addition, when subtracting polynomials, the sign of each term in the second polynomial needs to be changed (from positive to negative, or from negative to positive).
To know more about polynomials refer to the link brainly.com/question/11536910
#SPJ4
PLS HELP ME ANSWER THIS OR I CANT DO GYM TODAY

Answers
On the first part, just replace the variables with the given number to check.
1) 34 + 12 = 46 → Correct
2) 22 - 9 = 14 → Incorrect
3) 6 * 9 = 54 → Correct
4) 39 ^ 3 = 13 → Correct
On the second part, simply change the symbols. Like this:
5) 7 + k = 11 ⇒ 11 - 9 = k
K = 2
6) p - 24 = 13 ⇒ 13 + 24 = p
p = 37
7) b - 16 = 7 ⇒ 7 + 16 = b
b = 23
8) \(\frac{2}{5}\) + m = \(\frac{5}{6}\) ⇒ \(\frac{5}{6}\) - \(\frac{2}{5}\) = m
m = 13/30
Hope this helps!
Answer:
Step-by-step explanation:
i do not know sorry
ORCEE Exercise 1.9 (5 pts): What are the five permissible variable types in GAMS? Which type is most appropriate for a linear program (LP)?
Answers
The most appropriate variable type is usually level variables or positive variables for a linear program (LP).
In GAMS (General Algebraic Modeling System), there are several variable types available. The five permissible variable types in GAMS are:
1.These variables can take any real value within a defined range. They are typically used in models where quantities can vary continuously, such as production levels or resource allocations.
2.These variables are similar to level variables, but they are constrained to be non-negative. They are commonly used to represent quantities that cannot be negative, such as production quantities or inventory levels.
3.Binary variables can take only two possible values, typically 0 or 1. They are commonly used to represent decisions or choices, where 0 indicates the absence or non-selection of an option, and 1 indicates the presence or selection of an option.
4.Integer variables can take only integer values. They are used when the decision variables need to be restricted to whole numbers, such as representing the number of units to produce or the number of employees to hire.
5.These variables can take a value of either zero or any nonnegative real number within a specified range. They are used to model situations where there is a fixed cost associated with using a resource or when there are minimum usage requirements.
Learn more about linear program (LP) here:
https://brainly.com/question/32482420
#SPJ11
A soccer ball is kicked from the ground with an initial upward velocity of 90 feet per second. The equation h=-16t^2+90t gives the height h of the ball after t seconds.
a. Find the maximum height of the ball.
b. How many seconds will it take for the ball to reach the ground?
Answers
The ball reaches a height of 126.58 ft after 2.8125 seconds
Step-by-step explanation:
The maximum height of a parabola can always be found by looking for the vertex. You can find the x value (or in this case the t value) of a vertex by using -b/2a in which a is the coefficient of x^2 and b is the coefficient of x.
-b/2a
-(90)/2(-16)
-90/-32
2.8125 seconds
Now to find the height, we input that value in for t
h = -16t^2 + 90t
h = -16(2.8125)^2 + 90(2.8125)
126.58 feet
Write each fraction as a mixed number.
3 4/9
43/9
32/5
Answers
The value of the fractions in the mixed fraction form is 3(⁷/₉), 4(⁷/₉), and 6(²/₅) respectively.
What is a mixed fraction?A mixed fraction is a fraction that is created by fusing a fraction with a whole number. The fraction is defined as the division of the whole part into an equal number of parts.
The given fractions 34/9, 43/9, and 32/5 can be written in the form of the mixed fraction as below:-
To write the fractions in the form of the mixed fraction first divide the fraction by the complete number and put the remainder on the numerator.
34/9 = 3(⁷/₉)
43/9 = 4(⁷/₉)
32/5 = 6(²/₅)
Therefore, the value of the fractions in the mixed fraction form is 3(⁷/₉), 4(⁷/₉), and 6(²/₅) respectively.
To know more about a mixed fraction follow
https://brainly.com/question/1746829
#SPJ1
Determine the amplitude of the function y = negative one-half cosine x. On a coordinate plane, a function curves up from (0, negative 0.5) through (1.5, 0) to (3, 0.5). a. -1 c. One-half b. -Negative one-half d. 2
Answers
Step-by-step explanation:
The amplitude is the value that the cosine is being multiplied by.
The general equation of a sinusoid is
\( a \cos(b(x + c) ) + d\)
where a is the amplitude
\( \frac{2\pi}{ |b| } \)
is the period
-c is the phase shift
d is the midline(vertical shift)
Here the amplitude is -1/2 so b is the correct answer.
Answer:
the amplitude of the function that is y= -1/2 cos x, is 1/2.
Step-by-step explanation:
NEED URGENT HELP PLEASE!

Answers
The calculated volume of the model space is 1657.92 cubic inches
How to determine the volume of the model spaceFrom the question, we have the following parameters that can be used in our computation:
The model space made from:
A cone A cylinder A hemisphereThe volume of the model space is calculated as
Volume = Cone + Cylinder + Hemisphere
Using the volume formulas, we have
Volume = 1/3πr²h + πr²h + 2/3πr³
Substitute the known values in the above equation, so, we have the following representation
Volume = 1/3 * 3.14 * 6² * 8 + 3.14 * 6² * 8 + 2/3 * 3.14 * 6³
Evaluate
Volume = 1657.92
Hence, the volume of the model space is 1657.92 cubic inches
Read more about volume at
https://brainly.com/question/463363
#SPJ1
A Mass Of 1 Slug, When Attached To A Spring, Stretches It 2 Feet And Then Comes To Rest In The Equilibrium Position. Starting At T = 0, An External Force Equal To F(T) = 2 Sin 4t Is Applied To The System. Find The Equation Of Motion If The Surrounding Medium Offers A Damping Force That Is Numerically Equal To 8 Times The Instantaneous Velocity. (Use G =
A mass of 1 slug, when attached to a spring, stretches it 2 feet and then comes to rest in the equilibrium position. Starting at
t = 0,
an external force equal to
f(t) = 2 sin 4t
is applied to the system. Find the equation of motion if the surrounding medium offers a damping force that is numerically equal to 8 times the instantaneous velocity. (Use
g = 32 ft/s2
for the acceleration due to gravity.)
Answers
The general solution will depend on the values of k, m, and the damping coefficient 8/m. To find the equation of motion for this system.
We can use Newton's second law:
F = ma
where F is the net force acting on the system, m is the mass of the object, and a is the acceleration.
The net force in this case is the sum of the external force and the force due to the spring:
F = f(t) - kx
where k is the spring constant and x is the displacement from equilibrium.
The damping force is given as 8 times the instantaneous velocity, which we can write as:
F_damp = -8v
where v is the velocity of the object.
Putting everything together, we get:
m(d^2x/dt^2) = f(t) - kx - 8v
Substituting in the given values, we have:
1(d^2x/dt^2) = 2 sin 4t - kx - 8(dx/dt)
To simplify this equation, we can use the fact that x is a displacement and therefore the second derivative of x with respect to time is the acceleration. So we can rewrite the equation as:
a = (2/g)sin(4t) - (k/m)x - 8v/m
where g = 32 ft/s^2 is the acceleration due to gravity.
To solve for x, we can use the fact that the velocity is the derivative of displacement with respect to time:
v = dx/dt
Taking the derivative of the equation for velocity, we get:
a = d^2x/dt^2 = dv/dt = d/dt(dx/dt) = d/dt(v) = d/dt(-8v/m - (k/m)x + 2/g sin(4t))
Simplifying this expression, we get:
a = -8/m(dv/dt) - k/m(dx/dt) + (8/g)cos(4t)
Substituting in the value of a from the previous equation, we have:
(2/g)sin(4t) - (k/m)x - 8v/m = -8/m(dv/dt) - k/m(dx/dt) + (8/g)cos(4t)
Rearranging and simplifying, we get:
d^2x/dt^2 + (k/m + 8/m)dx/dt + k/mx = (16/g)cos(4t) - (2/g)sin(4t)
This is a second-order differential equation that we can solve using standard techniques, such as the method of undetermined coefficients or Laplace transforms. The general solution will depend on the values of k, m, and the damping coefficient 8/m.
Learn more about damping here:
https://brainly.com/question/30891056
#SPJ11
