What is the surface area of the rectangular prism?
5 m
10 m
2 m
Answers
The surface area of the rectangular prism is 160 square meters
What is the surface area of the rectangular prism?From the question, we have the following parameters that can be used in our computation:
5 m by 10 m by 2 m
The surface area of the rectangular prism is calculated as
Area = 2 * (5 * 10 + 5 *2 + 10 * 2)
Evaluate
Area = 160
Hence, teh area is 160 square meters
Read more about surface area at
https://brainly.com/question/26403859
#SPJ1
Related Questions
how many of each atom in the molecule cunh4cl3
Answers
Answer:
The chemical formula of Ammonium nitrate is NH4NO3. It consists of 2 nitrogen atoms, 3 oxygen atoms and 4 hydrogen atoms
Step-by-step explanation: 2.4088 x 10^24 atoms of H. Explanation: +5. how many hydrogen atoms are in one mole of CuNH4Cl3. 1 MOLECULE of CuNH4Cl3 contains 4 H
2.4088 x 10^24 atoms of H
A company uses sedans and minivans to produce custom vehicles for transporting hotel guests to and from airports. Plant A can produce 10 sedans and 8 minivans per week, and Plant B can produce 8 sedans and 6 minivans per week. How many weeks should each plant operate in order to produce at least 400 sedans? Express the answer as a linear inequality. Then, draw the graph and shade the feasible/solution region
Answers
To produce at least 400 sedans, we can set up the following inequality:
10x + 8y ≥ 400. Where x represents the number of weeks Plant A operates, and y represents the number of weeks Plant B operates.
To graph this inequality, we can rewrite it in slope-intercept form: y ≥ (-10/8)x + 50. The slope of the line is -10/8, and the y-intercept is 50. To plot the graph, we can draw a line with a slope of -10/8 passing through the point (0, 50). Then, we shade the region above the line to represent the feasible/solution region since we want y to be greater than or equal to the expression (-10/8)x + 50. The feasible region represents the combinations of weeks for Plant A and Plant B that will satisfy the condition of producing at least 400 sedans.
To know more about inequalities here: brainly.com/question/20383699
#SPJ11
a type of variable that can have an infinite number of values within a specified range is:
Answers
Answer: Continuous variables
A variable is said to be continuous if it can assume an infinite number of real values within a given interval
Step-by-step explanation: yep
A clothing business finds there is a linear relationship between the number of shirts, n, it can sell and the price, p, it can charge per shirt. In particular, historical data shows that 1,000 shirts can be sold at a price of $30, while 3,000 shirts can be sold at a price of $5. Find a linear equation in the form p(n)
Answers
Answer:
p=(-0.0125n) + 42.5
Step-by-step explanation:
Let p= price
n = number of shirts
m = slope of the line (note, the more shirts, the lower the price, so we know it's going to be negative)
b = y intercept
There are two points which are (1000, $30) and (3000, $5)
Our slope m = (p1-p2)/(n1-n2)
Filling in from our points m = (30-5)/(1000-3000)
m = 25/-2000
m = -0.0125
Since we have determined our slope, we can now find our equation
p-p1=m(n-n1)
p-30=(-0.0125)(n-1000)
p-30= (-0.0125n) + 12.5
p=(-0.0125n) + 42.5
Then, we can double check with the other point there:
p=(-0.0125n) + 42.5
5? (-0.0125x 3000) + 42.5
5= 5
Therefore,linear equation in the form p(n) is
p=(-0.0125n) + 42.5
use the parallel lines shown , what is m<2

Answers
Answer:
42
Step-by-step explanation:
138+42=180
and since they are parallel lines 1=2
1 = 42
2 = 42
please help me answer this!! im so confused

Answers
Answer:
178.7 ft.
Step-by-step explanation:
The kite is (x + 5) ft above the ground. So we need to find x first.
Use the trigonometric identity Sine.
\(Sin\ \theta=\frac{perpendicular}{hypotenuse}\\\\sin44=\frac{x}{250} \\\\x=250*sin44\\x=250*0.69\\x=173.66\ ft\\\)
Rounding your answer to the nearest tenth would be 173.7 ft.
Now the kite is above the ground x + 5 which means
173.7 + 5 = 178.7 ft.

-2x-3=y
Please give steps. This was due 4 days ago ;-;
Answers
Answer:
Step-by-step explanation:
Let's solve for x.
−2x−3=y
Step 1: Add 3 to both sides.
−2x−3+3=y+3
−2x=y+3
Step 2: Divide both sides by -2.
−2x
−2
=
y+3
−2
x=
−1
2
y+
−3
2
Answer:
x=-1/2y+-3/2 i have the answer but the shown work is messed up sorry
ASAP
What is the image of (-9,0) after a dilation by a scale factor of 3 centered at the origin?

Answers
Answer:
-27,0
Step-by-step explanation:
a lilypad doubles in size each day in 28 days the lilypad will cover the entire pond in how many days will the pond be half covered?
Answers
It will take 56 days for the lilypad to cover the entire pond. On day 28, the lilypad covers 1/2 of the pond, as we saw earlier.
The lilypad doubles in size each day, which means that if it covers a certain fraction of the pond on day n, it will cover twice that fraction on day n+1. In other words, if the lilypad covers 1/2^k of the pond on day k, then it will cover 1/2^(k-1) of the pond on day k+1.
If we let n be the number of days it takes for the lilypad to cover the entire pond, then we can say that on day n-28, the lilypad covers 1/2 of the pond (since on day n-28, the lilypad will be half the size of what it is on day n). Therefore, we want to solve for n-28 when the lilypad covers the entire pond, which is equivalent to the lilypad doubling in size 28 times:
1/2 * 2^28 = 2^(28-n+28)
Simplifying, we get:
2^(n-28) = 2^28
Taking the logarithm base 2 of both sides, we get:
n-28 = 28
Solving for n, we get:
n = 56
Therefore, it will take 56 days for the lilypad to cover the entire pond. On day 28, the lilypad covers 1/2 of the pond, as we saw earlier.
Learn more about "Fraction" : https://brainly.com/question/30154928
#SPJ11
Help asap have lesss then 14 minutes please

Answers
Answer:
m∠B = 31°
Step-by-step explanation:
To find m∠B, we use the theory that in order to get it we must find the difference between the two arcs GM and VR and dividing it into 2
When putting this to equation we get:
m∠B = \(\frac{1}{2}\) * (VR - GM) = \(\frac{1}{2}\) * ( 94° - 32°) = \(\frac{1}{2}\)(62°) = 31°
Which expression is equivalent to - 14 - 6?
O A. 14 + 6
O B. 14+(-6)
O c. -14 + 6
O D. -14 +(-6)
.
Answers
given center c and marked on circle c with being an inscribed angle, which is true?
Answers
Center C and \(~\overset{\LARGE{\frown}}{AD}\) marked on circle C with ∠AVD being an inscribed angle, the option 3) m ∠AVD = 1/2 \(m~\overset{\LARGE{\frown}}{AD}\) is true
It is given that C is a center of circle and ∠AVD is inscribed angle.
An inscribed angle is an angle with its vertex on the circle, formed by two intersecting chords. This common end point is the vertex of the angle. The measure of an inscribed angle is half the measure of the intercepted arc.
Inscribed Angle = 1/2 of Intercepted Arc
Therefore m ∠AVD = 1/2 \(m~\overset{\LARGE{\frown}}{AD}\)
So, the option 3) m ∠AVD = 1/2 \(m~\overset{\LARGE{\frown}}{AD}\) is true when center C and \(~\overset{\LARGE{\frown}}{AD}\) marked on circle C with ∠AVD being an inscribed angle
To know more about circle
https://brainly.com/question/4413349
#SPJ4
The complete question is in the image below

Condense
2loga(4)+3loga(X-4)loga(4)
Log(x+3)+log(x-3)
Answers should be log a x^3/16 and log (x^2-9)
SHOW WORK
URGENT
Answers
The steps to condensing the expressions
2loga(4)+3loga(X-4)loga(4)
Log(x+3)+log(x-3) is given below.
To condense the expressions, we can apply the properties of logarithms. Here are the condensed forms of the given expressions.
2loga (4) + 3loga(X - 4) - loga 4 )
By using the product and quotient rules of logarithms, we can simplify this expression as follows
2 loga( 4) + 3 loga( X-4) - log a(4)
= loga(4 ²) + loga((X-4)³) - loga (4) = loga (16 ) + loga((X-4)³) - loga (4)
Combining the logarithms using the power rule and quotient rule we have
= loga(16(X-4)³/4)
log(x+3) + log (x-3)
By using the product rule of logarithms, we can combine these logarithms
log (x +3) +log (x - 3) = log ((x +3 )(x -3 ))
Simplifying further, we get
= log (x² - 9 )
So this means that the condensed forms of the given expressions are
2loga( 4) + 3loga(X -4) - loga (4) = loga(16 (X-4) ³/4)
log (x+ 3) + log(x- 3) = log(x² - 9)
Learn more about condensed expressions:
https://brainly.com/question/13729452
#SPJ1
Bertha read 21 books. Each book had 155 pages. How many pages did she read altogether? 465 pages
3,155 pages
3,355 pages
3,255 pages
Answers
She read 3255 pages altogether.
Answer:
3,255 pages
Step-by-step explanation:
multiply 155 by 21
Predict the number of times you roll an odd number or a two when you roll a six-sided number cube 300 times.
Answers
Answer:
The probability of rolling an odd number or a two on a six-sided die is 1/2 + 1/6 = 2/3. This means that if you roll a six-sided die 300 times, you can expect to roll an odd number or a two approximately 200 times
Step-by-step explanation:
Answer: 400 TIMES
Step-by-step explanation:
1/6 +1/2
4/6
2/3
A normal population has a mean of $75 and standard deviation of $5. You select random samples of 40. a Apply the central limit theorem to describe the sampling distribution of the sample mean with » = 40. What condition is necessary to apply the central limit theorem?
Answers
The Central Limit Theorem states that for a random sample of n observations drawn from any population with a finite mean μ and a finite standard deviation σ, the sampling distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution.
To apply the Central Limit Theorem, the following condition is necessary:
1. The random sample should be selected from a population that has a finite mean (μ) and a finite standard deviation (σ).
In this case, the population mean is given as $75 and the population standard deviation is given as $5. Since both the mean and standard deviation are finite, the condition for applying the Central Limit Theorem is satisfied.
To know more about Limit visit:
brainly.com/question/12211820
#SPJ11
Ax+By=C form with slope of 14 over 13 with points (5,6) and (-8,-8)
Answers
\(\displaystyle\\Answer:\ -\frac{14}{13} x+y=\frac{8}{13}\)
Step-by-step explanation:
Ax+By=C the slope is 14/13 (5,6) (-8,-8)
The slope m equil 14/13
\(\displaystyle\\By=mx+C\\\\By=\frac{14}{13} x+C\ \ \ \ (1)\)
Substitute the coordinates of the points into equation (1) and obtain a system of equations:
\(\displaystyle\\\left \{ {{B(6)=\frac{14}{13}(5)+C } \atop {B(-8)=\frac{14}{13}(-8)+C }} \right.\\\\\left \{ {{6B=\frac{70}{13} +C\ \ \ \ \ \ \ (2)} \atop {-8B=-\frac{112}{13}+C\ \ \ (3) }} \right.\)
Multiply both parts of the equation (3) by -1:
\(\displaystyle\\\left \{ {{6B=\frac{70}{13}+C \ \ \ \ (4)} \atop {8B=\frac{112}{13}-C }} \right.\)
Add these equations :
\(14B=\frac{182}{14}\\\\ 14B=14\)
Divide both parts of the equation by 14:
\(B=1\)
Hence, let's substitute the value of B into equation (4):
\(\displaystyle\\6(1)=\frac{70}{13}+C \\\\6=\frac{70}{13}+C\\6-\frac{70}{13} =\frac{70}{13} +C-\frac{70}{13}\\\\\frac{6*13-70}{13}=C\\\\\frac{78-70}{13}=C\\\\\frac{8}{13}=C\\\)
\(\displaystyle\\Thus,\ C=\frac{8}{13}\\\\ So,\ 1(y)=\frac{14}{13} x+\frac{8}{13} \\ -\frac{14}{13} x+y=\frac{8}{13}\)
5. Jane invests $5,000 in a stock that loses 2% per year on average. Eqn:
Answers
Answer:
The equation would be 5000(1.02)^x with x representing the amount of years, as the values keep multiplying.
Step-by-step explanation:
please mark brainliest if you can thx <3
Answer:
5000(0.98)^x, with x being the amount of years
Substitute the expressions for length and width into the formula 2l 2w. distribute 2 to each term in the parentheses. combine like terms. inches
Answers
The perimeter of the rectangle with length 8x - 1 and width 10x + 3 is 20x + 6
What is perimeter of the rectangle?
The formula P=2l+2w, where l is the rectangle's length and w is its width, determines the perimeter P of a rectangle. The equation A=lw, where l is the length and w is the width, determines the area A of a rectangle.The perimeter of the rectangle with length 8x - 1 and width 10x + 3 is 20x+ 6
The formula for calculating the perimeter of a rectangle is expressed as:
P = 2( l + w)
Given the following parameters
length l = 8x - 1
width w = 2x + 4
Substitute the expressions for the length and width into the formula;
P = 2(8x - 1 + 2x + 4)
P = 2(10x + 3)
Distribute 2 over each term in the parenthesis
P = 2(10x) + 2(3)
P = 20x + 6
Hence the perimeter of the rectangle with length 8x - 1 and width 10x + 3 is 20x + 6.
Learn more about perimeter of the rectangle
brainly.com/question/897975
#SPJ4
The complete question is -
The perimeter formula for a rectangle is 2l + 2w, where l is the length and w is the width. Complete the steps to find an expression that represents the perimeter of the rectangle. Substitute the expressions for length and width into the formula 2l + 2w. Distribute 2 to each term in the parentheses. Combine like terms. inches
The graph of function f is shown. Use the zeros and the turning points of the graph to find the rule for f.
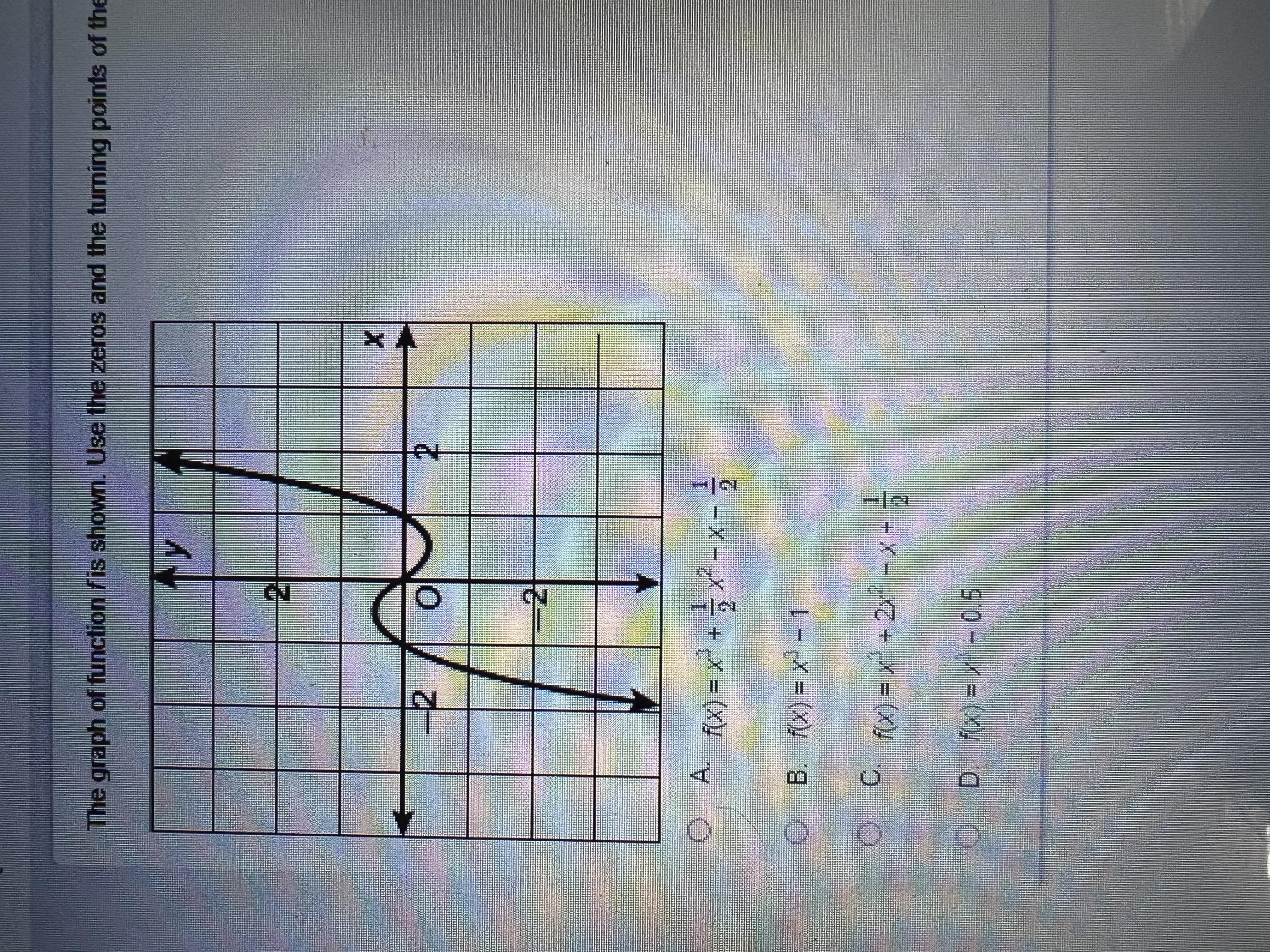
Answers
The equation to the function shown in the graph is f(x) = x³ - x because the x-intercepts are -1, 0, 1.
What is a function?It is defined as a special type of relationship, and they have a predefined domain and range according to the function every value in the domain is related to exactly one value in the range.
It is given that:
The graph of the function is shown in the picture.
From the graph of the function the x-intercepts are:
x = -1, 0, 1
The equation of the function can be written as:
f(x) = x(x + 1)(x - 1)
After multiplication:
f(x) = x(x² - 1)
f(x) = x³ - x
Thus, the equation to the function shown in the graph is f(x) = x³ - x because the x-intercepts are -1, 0, 1.
Learn more about the function here:
brainly.com/question/5245372
#SPJ1

For fixed population standard deviation and level of significance, the minimum sample size needed to guarantee a given margin of error ____________ as the margin of error increases.
Answers
Given margin of error increases as the margin of error increases.
To obtain a 3 percent margin of error at a 90% level of confidence, a sample size of about 750 is required. The sample size would be about 1,000 for a 95% level of confidence. Calculating the margin of error for various confidence levels is straightforward.
The ideal sample size for a population of 5,000 people has a 95% degree of confidence and a 5% margin of error, and it is 357. You may calculate this using our online calculator. This number can be used as a sample as well. It displays how many.
∴ For fixed population standard deviation and level of significance, the minimum sample size needed to guarantee a given margin of error increases as the margin of error increases.
Learn more about Margin Of Error here :
brainly.com/question/29982243
#SPJ4
PLEASE HELP ME ANYONE

Answers
i believe it’s (0,4) since it’s asking for vertex.
What is the equation of the line that passes through the point (3, -1) and is perpendicular to the equation y = -3x + 2? A. y=-3x+8
B. y = -3x
C. y=(1/3)x
D. Y =(1/3)x-2
Answers
Answer:
A) y = –3x+8
Step-by-step explanation:
first off, a negative equation means the graph is downward sloping from left to right –> \. So with this in mind you can immediately eliminate C and D because they are upward sloping graphs. B also doesn't work because it doesn't go through (3,–1). This leaves A as the right answer
the constant number is the number on the y-axis. So, for –3x+2, +2 is the y-coordinate on the y-axis. the slope is -3x meaning down 3, right 1. –3x+8 is the only answer that is perpendicular.
!!!!WILL MARK BRAINLIEST!!!! f(x) = x + 1 g(x) 2/x which polynomial is equivalent to (f o g)(x)
>CHECK PICTURE<

Answers
Answer:
C
Step-by-step explanation:
We are given that:
\(\displaystyle f(x)=x+1\text{ and } g(x)=\frac{2}{x}\)
And we want to find:
\(f(g(x))\)
Therefore, we will substitute the equation for g(x) for the x in f(x). This yields:
\(\displaystyle f(g(x))=\big(\frac{2}{x}\big)+1\)
Simplify:
\(\displaystyle f(g(x))=\frac{2}{x}+1\)
Hence, our answer is C.
If the equations below are true, find the value of x + z.
(4x + 2y + 8z = 30
(3x +2y + 7z = 24
Answers
If the given equations are true, then the value of x + z is 6.
Simultaneous equations or systems of equations are two or more equations in algebra that must be solved jointly. The number of equations must match the number of unknowns for a system to have a singular solution.
Consider the equations are true,
4x + 2y + 8z = 30 ------------(1)
3x + 2y + 7z = 24 ------------(2)
Now,
By subtracting equation (2) from equation (1) we get:
eq(1) - eq(2)
4x + 2y + 8z - ( 3x + 2y + 7z ) = 30 -24
4x + 2y + 8z - 3x - 2y - 7z = 6
( 4x - 3x ) + ( 2y - 2y ) + ( 8z - 7z ) = 6
x + 0 + z = 6
x + z =6
Therefore, assuming the equations to be true the value of x + z is equal to 6.
Learn more about equations here:
https://brainly.com/question/2972832
#SPJ9
Use a two-dimensional representation of the prism, if necessary, to find the area of the entire surface of the prism.
The surface area of the prism is square units.

Answers
Answer:
2((5)(4) + (5)(3) + (4)(3)) = 2(20 + 15 + 12)
= 2(47) = 94
20) Find angle Dd= 54.9 cm, f= 69.2 cm, F = 56°

Answers
Using sine rule formula to resolve the value for angle D
The sine rule formula is,
\(\frac{sinD}{d}=\frac{sinF}{f}\)Given:
\(\begin{gathered} d=54.9cm \\ f=69.2cm \\ F=56^0 \end{gathered}\)Therefore,
\(\frac{sinD}{54.9}=\frac{sin56^0}{69.2}\)Simplify
\(\begin{gathered} sinD=\frac{54.9\times sin56^0}{69.2}=0.65771911464 \\ D=sin^{-1}(0.65771911464)=41.12615063003\approx41^0(nearest\text{ degree\rparen} \\ D=41^0 \end{gathered}\)Hence, the answer is
\(\angle D=41^0\)HELP PLEASE!!!!!!!!!!!!!

Answers
Answer:
2
Step-by-step explanation:
Write your equation with "M" isolated.4 Hours (H) 36 Miles (M)
Answers
How do i solve this?
I dont understand what the big number is to the small number

Answers
The red figure is smaller so it is a reduction.
To find the scale factor divide the length of the smaller shape by the length of the larger shape:
9/15 this can be reduced to 3/5