What is the slope of y = -4x - 3
Answers
Answer:
-4
Step-by-step explanation:
Answer:s
slope of -4x-3: m=-4
Related Questions
is a pipe is 24000 km long how much would one km be?
Answers
0.0000416 pipe is the number of pipe for 1 km lenght
Ratio and proportionProportion is defined as the ratio os two quantity for instance numbers.
According to the given question, the length of one pipe is equivalent to 24000km. We are to determine the number of pipe that 1 km will be.
This is expressed as:
Number of pipe for 1 km = Number of pipe/Total km
Number of pipe for 1 km = 1/24000
Number of pipe for 1 km = 0.0000416 pipe
Hence the amount of pipe for 1 km is 0.0000416 pipe
Learn more on ratio and proportion here: https://brainly.com/question/3796978
#SPJ1
A poll taken by GSS asked whether people are satisfied with their financial situation. A total of 478 out of 2038 people said they were. The same question was asked two years later, and 537 out of 1967 people said they were. Get a 90% confidence interval for the increase in the proportion of people who were satisfied with their financial condition. The CI is
Answers
We can say with 90% confidence that the increase in proportion of people satisfied with their financial situation is between 1.05% and 6.71%.
To calculate the confidence interval for the increase in proportion of people satisfied with their financial situation, we need to first calculate the proportions for both years:
Proportion in year 1 = 478/2038 = 0.2342
Proportion in year 2 = 537/1967 = 0.2730
The increase in proportion is:
0.2730 - 0.2342 = 0.0388
To calculate the confidence interval, we can use the formula:
CI = (point estimate ± (critical value x standard error))
The point estimate is the increase in proportion we just calculated: 0.0388
The critical value can be found using a z-table for a 90% confidence level. The z-value for a 90% confidence level is 1.645.
The standard error can be calculated using the formula:
sqrt[(p1(1-p1)/n1) + (p2(1-p2)/n2)]
where p1 and n1 are the proportion and sample size for year 1, and p2 and n2 are the proportion and sample size for year 2.
Plugging in the values, we get:
SE = sqrt[(0.2342(1-0.2342)/2038) + (0.2730(1-0.2730)/1967)] = 0.0174
Now we can plug in all the values to get the confidence interval:
CI = (0.0388 ± (1.645 x 0.0174)) = (0.0105, 0.0671)
Know more about 90% confidence here:
https://brainly.com/question/31420373
#SPJ11
Consider the uniformly charged disk shown in 26.16. What is the magnitude of the electric field on the z axis in that figure, for z >> R?
A. E=kQ/R2
B. E=-kQ/R2
C. E=kQ/z2
D. E=-kQ/z2
Answers
The magnitude of the electric field on the z-axis, when z >> R, is given by E = kQ / z² (option c).
According to Gauss's law, the electric flux through the cylindrical Gaussian surface is directly proportional to the charge enclosed within it. Since the charge enclosed by the Gaussian surface is the charge of the disk (Q), the electric flux is given by:
Flux = Q / ε₀
Where ε₀ is the permittivity of free space. The electric flux can also be expressed as the product of the electric field (E) and the area of the cylindrical surface (A), which is 2πR times the height (h) of the cylinder:
Flux = E * A
Substituting the expressions for the flux and the area, we have:
E * 2πR * h = Q / ε₀
The height (h) of the cylinder cancels out, and rearranging the equation gives:
E = Q / (2πR * ε₀)
Now, we need to express the charge (Q) in terms of the known quantities. Since the disk is uniformly charged, we can express its charge in terms of its charge density (σ) and its area (A):
Q = σ * A
The area of the disk is given by A = πR². Substituting this into the equation, we have:
Q = σ * πR²
Substituting this expression for Q back into the equation for the electric field (E), we get:
E = (σ * πR²) / (2πR * ε₀)
Simplifying further, we find:
E = σR / (2ε₀)
This means that the correct option for the magnitude of the electric field is option C: E = kQ / z², where k is a constant related to the permittivity of free space.
To know more about magnitude here
https://brainly.com/question/31022175
#SPJ4
May i get some help please
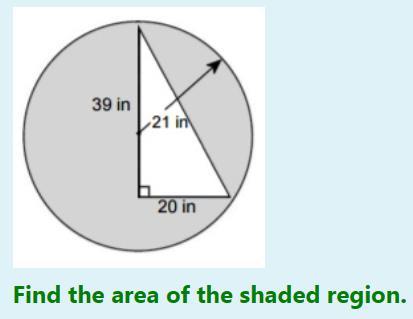
Answers
Answer:
\(\huge\boxed{\sf 995.4 in.\²}\)
Step-by-step explanation:
Area of the circle:
= πr²
Where r = 21 in.
= (3.14)(21)²
= (3.14)(441)
= 1385.4 in.²
Area of triangle:
= \(\sf \frac{1}{2} (Base)(Height)\)
Where Base = 20 in. , Height = 39 in.
= \(\sf \frac{1}{2} (20)(39)\)
= (10)(39)
= 390 in.²
Area of the shaded region:
= Area of the circle - Area of the triangle
= 1385.4 - 390
= 995.4 in.²
\(\rule[225]{225}{2}\)
Hope this helped!
~AH1807Find the area of an isosceles triangle with a vertex angle of 22 degrees and a leg length of 5. Round to the nearest tenth.
Answers
The area of the Triangle given in the question is 4.7
Area of Triangle = 1/2(base × height )
Using the vertex , we can obtain the height of the triangle thus:
sin(22 degrees) = h/5height = 1.873
Inserting the parameters into the Area formula :
height = 1.873
base = 5
Area of Triangle = 1/2 × 5 × 1.873
Area of Triangle= 4.68
Therefore, the area of the triangle is 4.7
Learn more on area of Triangle: https://brainly.com/question/17335144
#SPJ1
Let A be a 2x 6 matrix. What must aland & be f we define the linear transformation by T : R" → R as T z)-Az 꺼
Answers
If A = [a₁ a₂ a₃ a₄ a₅ a₆], where each aᵢ is a column vector in R², and z = [z₁ z₂ z₃ z₄ z₅ z₆] is a vector in R⁶, then T(z) = Az can be written as:T(z) = z₁a₁ + z₂a₂ + z₃a₃ + z₄a₄ + z₅a₅ + z₆a₆.
Let A be a 2x6 matrix. If we define the linear transformation T: R⁶ → R² as T(z) = Az, then the number of columns in matrix A must be equal to the dimension of the domain of T, which is 6. The number of rows in matrix A must be equal to the dimension of the range of T, which is 2. Therefore, A must be a 2x6 matrix.If we plug in a vector z from the domain of T, which is R⁶, into T(z), then we get a vector in the range of T, which is R². The entries of the output vector are obtained by taking linear combinations of the columns of matrix A, where the coefficients are the entries of z.
In other words, the i th entry of the output vector is obtained by multiplying the ith row of matrix A with the vector z, and then adding up the products. So, if A = [a₁ a₂ a₃ a₄ a₅ a₆], where each aᵢ is a column vector in R², and z = [z₁ z₂ z₃ z₄ z₅ z₆] is a vector in R⁶, then T(z) = Az can be written as:T(z) = z₁a₁ + z₂a₂ + z₃a₃ + z₄a₄ + z₅a₅ + z₆a₆.
To know more about column vector visit:-
https://brainly.com/question/31816488
#SPJ11
the null hypothesis for the single factor anova states that all means are equal.
T/F
Answers
The null hypothesis for the single factor ANOVA states that all means are equally true.
The null hypothesis for a single-factor ANOVA (analysis of variance) states that all means are equal.
The alternative hypothesis, on the other hand, suggests that at least one of the means is different from the others.
The purpose of the ANOVA test is to determine whether there is sufficient evidence to reject the null hypothesis and conclude that there are significant differences between the means. A statistical formula used to compare variances across the means (or average) of different groups.
Hence, the statement is true .
To know more about null hypothesis click here :
https://brainly.com/question/30821298
#SPJ4
what is 4 + 1
cause i'm stuck on this question hehe
Answers
Explernation:
Yee Welcome.
Have a great day!
Answer:
5
Step-by-step explanation:
4+1=5...if you add the number 4 and 1 it gives 5 lol
Let fx) = x + 11 + 2 and g(x) - 2 x + 11. When does f(x) = g(x)?
Answers
Answer:when x= -2/3
That means, when the common product of f(x) & g(x) is x+2/3
Step-by-step explanation:
The number 175 is 25% of what number?
Answers
Answer: 700
Step-by-step explanation:
175 * 4 = 700
Answer:
700
Step-by-step explanation:
To solve this problem you multiply 175 by 100 and then divide the total by 25 as follows: (175 x 100) / 25
When we put that into our calculator, we get the following answer:
700
Please help! This is for my math class its due tomorrow

Answers
Answer:
negative one third
Step-by-step explanation:
So you go to the 1 and half
The circumference, or perimeter, of a circle can be found by multiplying its diameter by 3.14. What is the circumference of a circle that has a diameter of 1/2? Express your answer as a decimal.
Answers
Find the rectangular coordinate for the polar coordinate (4,210^0)
Please I will give Brainly
Answers
The rectangular coordinate for the polar coordinate (4, 210°) is (-3.46, -2).
What is the rectangular coordinate?The rectangular coordinate for the polar coordinate (4, 210°) is calculated by applying the following formula as shown below;
x = r cos(θ)
y = r sin(θ)
where;
r is the distance from the origin of the coordinateθ is the angle or directionFrom the given polar coordinate (4, 210°);
r = 4
θ = 210⁰
The rectangular coordinate is calculated as follows;
x = 4 x cos(210°)
y = 4 x sin(210°)
x = -3.46
y = -2
Learn more about rectangular coordinate here: https://brainly.com/question/1402079
#SPJ1
Plz help fast take a picture of your work

Answers
Answer:
1: logical
2: Organic
3: Global
4: Classical
5: Musical
6: logical
7: editoral
8: Analytical
Step-by-step explanation:
I tried my best
Solve the expression 1/8 + 1/4 How did you find the answer?
Answers
Answer:
3/8 or 0.375
Step-by-step explanation:
1/8 + 1/4
1/8+ 1*2/4*2
1/8+2/8
1+2/8
3/8
0.375
anais bought yards of ribbon. she had feet inches of ribbon left after trimming some curtains. how many inches of ribbon did anais use to trim the curtains? anais used blank inches of ribbon. the solution is
Answers
Anais, who bought a ribbon of length \(2 \dfrac 12 \) yards, and she trimming a curtain from it. From substraction, length of ribbon used in curtain is equals to 72 inches.
Word problems express in mathematical form. In subtraction, keywords that could signal the operation are lesser, less than, removed from. However, there are times when the idea of subtraction or taking away is inferred from the problem itself. In the problem, total length of ribbon Anais bought
= \(2 \dfrac 12 \) yards
The length of ribbon left after trimming some curtains = 1 feet 6 inches
We have to determine inches of ribbon Anais use to trim the curtains. Let it will be equal to x inches . We may notice in the provide values that they all have different units. We can convert the all different units into inches. Using uint conversation, 1 yard = 36 inches
=> \(2 \dfrac 12 \)
yards =\( 36 × \frac{ 5}{2} \)
= 90 inches
Similarly, 1 feet = 12 inches, then 1 feet + 6 inches = 12 + 6 = 18 inches
Thus, the left ribbon length = 18 inches
Using substraction method, the length in inches of ribbon that anais use to trim the curtains = total length - left length of ribbon = 90 - 18
= 72 inches.
Hence, required value is 72 inches.
For more information about substraction, visit :
https://brainly.com/question/22520797
#SPJ4
Complete question:
Anais bought
\(2 \dfrac 12 \)
yards of ribbon. She had 1 feet 6 inches of ribbon left after trimming some curtains. How many inches of ribbon did Anais use to trim the curtains?
another financial analyst, who also works for the online trading platform, claims their clients have a lower proportion of stock portfolios that contain high-risk stocks. this financial analyst would like to carry out a hypothesis test and test the claim that the proportion of stock portfolios that contain high-risk stocks is lower than 0.10. why is their hypothesis test left-tailed?
Answers
The hypothesis test is left-tailed because the financial analyst wants to test if the proportion of stock portfolios containing high-risk stocks is lower than 0.10.
In other words, they are interested in determining if the proportion is significantly less than the specified value of 0.10. A left-tailed hypothesis test is used when the alternative hypothesis suggests that the parameter of interest is smaller than the hypothesized value. In this case, the alternative hypothesis would be that the proportion of stock portfolios with high-risk stocks is less than 0.10.
By conducting a left-tailed test, the financial analyst is trying to gather evidence to support their claim that their clients have a lower proportion of high-risk stock portfolios. They want to determine if the observed data provides sufficient evidence to conclude that the true proportion is indeed less than 0.10, which would support their claim of a lower proportion of high-risk stocks.
Therefore, a left-tailed hypothesis test is appropriate in this scenario.
Learn more about financial here
https://brainly.com/question/31299651
#SPJ11
The cafeteria offered an apple a fruit choice six days out of ten days. which equivalent form of decimal, fraction, and/or percent is equivalent to the fraction of days the cafeteria offered an apple as a fruit choice?
Answers
The fraction of days the cafetaria offered an apple as a fruit choice is 6/10. The equivalent form of decimal is 0.6, the equivalent form of fraction is 3/5, and the equivalent form of percentage is 60%.
What is a fraction?A fraction is a ratio of two numbers, mathematically expressed as a/b where a is the numerator and b is the denominator. That mathematical expression is the common form of fraction. Fractions can take a number of forms, such as decimal and percentage.
Decimals are numbers that consist of two parts, which are the whole number part and the fractional part. 0.6 is the decimal form of fraction 6/10.
Percentage is a relative value that indicates hundredth parts of a quantity. 60% is the percent form of fraction 6/10.
Finally, we can simplify 6/10 to get 3/5: \(\frac{6}{10} =\frac{6\div 2}{10\div 2}=\frac{3}{5}\).
Learn more about fractions here: https://brainly.com/question/17220365
#SPJ4
What is the product of 2x3 +9 and x3 +7?
Answers
The product of the expression is 2x⁶ + 23x³ + 63
How to determine the productFirst, we should note that algebraic expressions are described as expressions that are composed of coefficients, terms, constants, variables and factors.
These algebraic expressions are also made up of mathematical operations, such as;
BracketAdditionMultiplicationDivisionParenthesesSubtractionFrom the information given, we have that;
2x3 +9 and x3 +7?
Then,
(2x³ + 9)(x³ + 7)
expand the bracket
2x⁶ + 14x³ + 9x³ + 63
add like terms
2x⁶ + 23x³ + 63
Learn about algebraic expressions at: https://brainly.com/question/4344214
#SPJ1
PLEASE HELP!! Will mark Brainliest!
This unit is about polynomial and rational functions. What is a polynomial? What is a rational function? Are all polynomials rational functions, why or why not?
Answers
Answer:
What is a polynomial?
- In mathematics, a polynomial is an expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables
What is a rational function?
- In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials.
Are all polynomials rational functions?
.A function that cannot be written in the form of a polynomial, so no they are not all functions.
Evaluate the following algebraic expression, if (x = 5, y = 3)
x² +9y - 5
Answers
Answer: 47
Step-by-step explanation:
simply substitute the constants with 5 and 3.
(5)^2 + 9(3) - 5 = 47
5 squared+9(3)-5. 5 squared is 25. 9(3) is 27. 25+27-3 equals 49
What is the highest power of 2 that is less than 1000? Enter result of 2
∧
N, not just the power N. Question 4 Express this hexadecimal number in decimal: 4AF
Answers
Question 1: The highest power of 2 that is less than 1000 is 2^9 = 512.
Question 4: The decimal equivalent of the hexadecimal number 4AF is 1199.
Question 1: What is the highest power of 2 that is less than 1000?
We know that,
2^ {10} = 1024 which is the smallest number greater than 1000.
Therefore, the highest power of 2 that is less than 1000 is 2^ 9
2^ (9) = 512
Question 2: Express this hexadecimal number in decimal: 4AF
To convert hexadecimal number to decimal number, we multiply each digit of the hexadecimal number by its place value and add the products. We can start from the right and work our way to the left.
4AF in hexadecimal is equal to:
(4 × 16²) + (10 × 16¹) + (15 × 16⁰)
= 1024 + 160 + 15
= 1199
Therefore, the decimal equivalent of the hexadecimal number 4AF is 1199.
Learn more about hexadecimal from the link
https://brainly.com/question/11109762
#SPJ11
Guess my rule. PLS HELP ME I BEG

Answers
Answer:
12,22,2002, 4x, 5x
Step-by-step explanation:
The rule is x2 +2
Not sure on the last 4
Sorry I answered late.
The graph of y = |x − 3| + 2 is reflected across the x-axis and then translated down 2 units. What is an equation of the transformed graph?
Answers
Answer:
y=-|x − 3|
Work
y = |x − 3| + 2
-2 -2
y = |x − 3|
add a neg before the absolute value
y=-|x − 3|
Transformation involves changing the position of a graph
The equation of the transformed graph is \(\mathbf{y = -|x -3| - 4}\)
The equation is given as:
\(\mathbf{y = |x -3| + 2}\)
The rule of reflection across the x-axis is:
\(\mathbf{(x,y) \to (x,-y)}\)
So, we have:
\(\mathbf{y = -|x -3| - 2}\)
The rule of translation 2 units down is:
\(\mathbf{(x,y) \to (x,y-2)}\)
So, we have:
\(\mathbf{y = -|x -3| - 2 - 2}\)
\(\mathbf{y = -|x -3| - 4}\)
Hence, the equation of the transformed graph is \(\mathbf{y = -|x -3| - 4}\)
Read more about transformation at:
https://brainly.com/question/11707700
during an election, a group of 4 council members must be selected from a group of 18 people running for these positions. how many such selections are possible?
Answers
The possible number of ways of selection by using combination formula is 3060.
What is combination?
A grouping of items where the order in which they were chosen is irrelevant is known as combination.
Given that the number of people in the group is 18. Only 4 people will be member of the council.
The formula of combination is \(^{n}C_{r}=\frac{n!}{r!(n-r)!}\) , where r number of objects are selected from n objects.
In the given question the value of n is 18 and the value of r is 2.
Substitute the value of n and r in \(^{n}C_{r}=\frac{n!}{r!(n-r)!}\).
\(^{18}C_{4}=\frac{18!}{4!(18-4)!}\)
Solve the above expression:
18^C_4 = 18x17x16x15x14/4x14
18^C_4 = 18x17x16x15/4x3x2x1
3060 18^C_4 = 3060
The number of ways such selection is 3060.
To learn more about combination, you can visit below link:
https://brainly.com/question/28065038
#SPJ4
Find the sum of the first 11 terms of the geometric sequence shown below.
- 3/2, 3, -6, 12, ...
Answers
The sum of the first 11 terms of the geometric sequence -3/2, 3, -6, 12, ... is 1092. A geometric sequence is a sequence where each term is found by multiplying the previous term by a constant factor
In this case, the common ratio is -2. To find the sum of the first 11 terms, we can use the formula for the sum of a geometric series:
S = a(1 - r^n) / (1 - r)
where S is the sum of the series, a is the first term, r is the common ratio, and n is the number of terms. Plugging in the values, we get:
S = (-3/2)(1 - (-2)^11) / (1 - (-2))
Simplifying the equation gives:
S = (-3/2)(1 - 2048) / 3
S = (-3/2)(-2047) / 3
S = 3069/2
S = 1534.5
Therefore, the sum of the first 11 terms of the given geometric sequence is 1534.5.
Learn more about geometric series: brainly.com/question/24643676
#SPJ11
Hi, this is 3 questions In one! 1. Solve and simplify. 2/7 divided by 4/5
2. Convert the fraction to a decimal: 38/333
3. Convert the fraction to a decimal 12/111
THIS IS 3 in 1

Answers
Step-by-step explanation:
1.5/14
2.0.114114114....
3.0.108108108
plssss mark me brainliest
1. Ans; The choose D. 5/14
\( \frac{2}{7} \div \frac{4}{5} \\ \\ \frac{2}{7} \times \frac{5}{4} = \frac{5}{14} \)
2. Ans; The choose B.(No D.)
\( \frac{38}{333} = 0.114\)
3. Ans; The choose D.\( \frac{12}{111} = \frac{4}{37} = 0.108\)
I hope I helped you^_^
In the diagram beside QRS is a straight line QP/RT ‹ PRQ = 56 ‹ QPR = 84 and ‹+RS X° X find x

Answers
Answer:
x = 40
Step-by-step explanation:
< PQR = 180° - (84° + 56°)
= 40°
so x = 40° (corresponding angles QP// RT)
The sum of two numbers is 30 and their product is 209. Find the numbers.
Answers
Taking into account the definition of a system of linear equations, if the sum of two numbers is 30 and their product is 209, the number are 11 and 19.
Definition of system of linear equationsSystems of linear equations are groupings of first degree equations with the same unknowns, of which a common solution must be found.
Solving a system of equations consists of finding the value of each unknown so that all the equations of the system are satisfied.
Numbers in this caseIn this case, a system of linear equations must be proposed taking into account that "x" and "y" are two numbers.
You know:
The sum of two numbers is 30.The product of the two is 209.So, the system of equations to be solved is
x + y= 30
x×y=209
It is decided to solve it using the substitution method, which consists of clearing one of the two variables in one of the equations of the system and substituting its value in the other equation.
In this case, isolating "x" from the first equation:
x= 30 - y
Substituting the expression in the second equation:
(30 - y)×y=209
Solving:
30y - y×y=209
30y - y² - 209= 0
Being this a quadratic function of the form ax² + by +c, then it can be solved by: \(x1,x2=\frac{-b+-\sqrt{b^{2}-4ac } }{2a}\)
In this case, being a=-1, b=30 and c=-209, the equation is solved by:
\(y1=\frac{-30+\sqrt{30^{2}-4x(-1)x(-209) } }{2x(-1)}\)
\(y1=\frac{-30+\sqrt{900-836 } }{-2}\)
\(y1=\frac{-30+\sqrt{64} }{-2}\)
\(y1=\frac{-30+8}{-2}\)
\(y1=\frac{-22}{-2}\)
y1= 11
Remembering that x= 30 - y, you get:
x1= 30 -11
x1= 19
and
\(y2=\frac{-30-\sqrt{30^{2}-4x(-1)x(-209) } }{2x(-1)}\)
\(y2=\frac{-30-\sqrt{900-836 } }{-2}\)
\(y2=\frac{-30-\sqrt{64} }{-2}\)
\(y2=\frac{-30-8}{-2}\)
\(y2=\frac{-38}{-2}\)
y2= 19
Remembering that x= 30 - y, you get:
x2= 30 - 19
x2= 11
Finally, the number are 11 and 19.
Learn more about system of equations:
brainly.com/question/14323743
#SPJ1
3.18 a continuous random variable x that can assume values between x = 2 and x = 5 has a density function given by f(x) = 2(1 x)/27. find (a) p(x < 4); (b) p(3 ≤ x < 4).
Answers
For the given continuous random variable x:
(a) p(x < 4) = -8/27.
(b) p(3 ≤ x < 4) = -5/27
The continuous random variable x that can assume values between x = 2 and x = 5 has a density function given by f(x) = 2(1 x)/27.
(a) To find p(x < 4), we need to integrate the density function from x = 2 to x = 4:
p(x < 4) = ∫24 2(1 x)/27 dx
= (2/27) ∫24 (1 - x) dx
= (2/27) [(x - x2/2)]24
= (2/27) [(4 - 42/2) - (2 - 22/2)]
= (2/27) [(4 - 8) - (2 - 2)]
= (2/27) [(-4) - 0]
= (2/27) (-4)
= -8/27
So, p(x < 4) = -8/27.
(b) To find p(3 ≤ x < 4), we need to integrate the density function from x = 3 to x = 4:
p(3 ≤ x < 4) = ∫34 2(1 x)/27 dx
= (2/27) ∫34 (1 - x) dx
= (2/27) [(x - x2/2)]34
= (2/27) [(4 - 42/2) - (3 - 32/2)]
= (2/27) [(4 - 8) - (3 - 4.5)]
= (2/27) [(-4) - (-1.5)]
= (2/27) (-2.5)
= -5/27
So, p(3 ≤ x < 4) = -5/27.
Know more about continuous here:
https://brainly.com/question/18102431
#SPJ11