Answers
The slope of the line = 4
Explanation:Select two points on the line
(0, 0) and (1, 4)
That is, x₁ = 0, y₁ = 0, x₂ = 1, and y₂ = 4
The slope of the line is calculated as:
\(\begin{gathered} Slope=\frac{y_2-y_1}{x_2-x_1} \\ \\ Slope=\frac{4-0}{1-0} \\ \\ Slope=\frac{4}{1} \\ \\ Slope=4 \end{gathered}\)The slope of the line = 4
Related Questions
Howdy! Thanks for stopping by my question! I would really appreciate the help! I've attached the question below. Thanks!
I'd appreciate if you made sure to double check your answers and provide everything the question is asking! INCLUDE ALL STEPS!

Answers
Answer:
a) x = 1 ± (3/7)√7
b) (-∞, -5) ∪ [-2, 5) ∪ [6, ∞)
Step-by-step explanation:
You want solutions to the relations ...
7 +1/x = 1/(x-2)(x² -4x -12)/(x² -25) ≥ 0a) 7 + ...We like to solve these in the form f(x) = 0. It helps avoid extraneous solutions.
\(7+\dfrac{1}{x} -\dfrac{1}{x-2}=0\\\\\\\dfrac{7x+1}{x}-\dfrac{1}{x-2}=0\\\\\\\dfrac{(7x+1)(x-2)-x}{x(x-2)}=0\\\\\\ \dfrac{7x^2-14x-2}{x(x-2)}=0\)
The roots of the numerator quadratic are found by ...
x² -2x -2/7 = 0 . . . . . divide by 7
x² -2x +1 -9/7 = 0 . . . . add and subtract 1
(x -1)² = 9/7 . . . . . . . . . . write as a square, add 9/7
x -1 = ±√(9·7/49) = ±(3/7)√7 . . . . take the square root
x = 1 ± (3/7)√7
b) (x² - ...Rational inequalities are best solved by identifying the roots of numerator and denominator. These tell you where the function changes sign. The end behavior of the rational function tells you what the signs are changing from.
\(\dfrac{x^2-4x-12}{x^2-25}\ge 0\\\\\\\dfrac{(x+2)(x-6)}{(x+5)(x-5)}\ge0\)
This has a horizontal asymptote at y=1 for |x|→∞. It has vertical asymptotes at x=±5.
The sign changes occur at x ∈ {-5, -2, 5, 6}. The rational expression is positive (approaching +1) for x < -5 and for x > 6. It is negative in the adjacent intervals, so positive again for -2 < x < 5.
The inequality is satisfied for ...
x < -5-2 ≤ x < 56 ≤ xI. What is
42% of
18?
need help fast!
Answers
Answer:
It is 7.56!
Other:
Brainliest? Thanks!
simplify to lowest form.
a. 1/2 + 3/2 = ?
b. 2/5 + 3/5 = ?
Answers
for letter b the answer is 1
Answer:
A= 2 B= 1
Step-by-step explanation:
1/2 +3/2= 4/2 than divide 4/2 by 2 it will give you 2/1 so 2/1 equal 2 because 2 is bigger than 1
2/5 + 3/5 = 5/5 it is 1 because if you divide it by 5 you will get a whole number which is 1
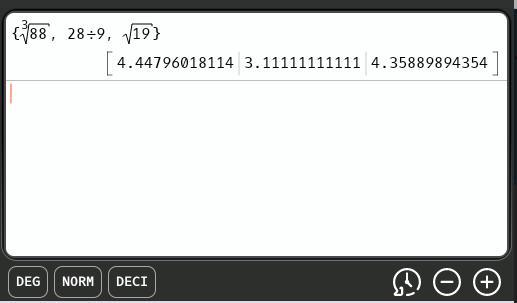
Order cube root of eighty-eight, twenty-eight ninths, square root of nineteen from greatest to least.
cube root of eighty-eight, twenty-eight ninths, square root of nineteen
twenty-eight ninths, square root of nineteen, cube root of eighty-eight
twenty-eight ninths, cube root of eighty-eight, square root of nineteen
cube root of eighty-eight, square root of nineteen, twenty-eight ninths
Answers
Answer:
(a) twenty-eight ninths, square root of nineteen, cube root of eighty-eight
Step-by-step explanation:
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.
OrderThe attachment shows the ordering, least to greatest, to be ...
\(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)
__
Additional comment
We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.
One way to do the comparison is to convert these to values that need to have the same root:
√19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)
∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)
The roots will have the same ordering as 19³ and 88².
Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...
19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859
88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744
Then the ordering is ...
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Answer:
the ordering is
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Step-by-step explanation:
s equivalent to the expression (3 x 100) + (5 × 1) + (9×) + (1x)²
100
What is a decimal that is
?
Answers
The decimal number that represents the expression (3 * 100) + (7 * 10) + (5 * 1) + (9 * 0.01) + (2 * 0.001) is; 375.092
How to convert numbers to decimal?
We want to find the decimal that is equivalent to the expression (3 * 100) + (7 * 10) + (5 * 1) + (9 * 0.01) + (2 * 0.001).
Thus, we have;
(3 * 100) = 300
(7 * 10) = 70
(5 * 1) = 5
(9 * 0.01) = 0.09
(2 * 0.001) = 0.002
Thus, the given initial expression can now be written as;
300 + 70 + 5 + 0.09 + 0.002 = 375.092
Thus, the decimal number that represents the expression
(3 * 100) + (7 ** 10) + (5 * 1) + (9 * 0.01) + (2 * 0.001) is; 375.092
The complete question is;
What is a decimal that is equivalent to the expression (3 * 100) + (7 ** 10) + (5 * 1) + (9 * 0.01) + (2 * 0.001)?
Read more about decimals at; https://brainly.com/question/7978210
#SPJ1
What is the common ratio of the geometric sequence?
Number graph ranging from zero to ten on the x axis and zero to twenty-eight on the y axis. Points are plotted on the graph at (one, eight), (two, twelve), (three, eighteen) and (four, twenty-six point five). The points form a general positive trend.
Answers
A geometric series is one in which there is a constant between two successive numbers in the series.
What is geometric progression?When there is a constant between the two successive numbers in the series then it is called a geometric series. In other words, every next term is multiplied by that constant term to form a geometric progression.
The sequence in which every next number is the addition of the constant quantity in the series is termed the arithmetic progression
Suppose the series is given as
2,4,8,16,32,64.........
The common difference is defined as the ratio of the next term to the previous term.
From the above series, the common ratio is calculated as,
Common ratio = 4 / 2
Common ratio = 2
To know more about geometric progression follow
https://brainly.com/question/12006112
#SPJ1
what is the length of ac brainly
Answers
The length of AC is equal to 5 units.
Given:
From the figure :
ΔABC is a right angled triangle with sides:
AB = 3 and BC = 4
Right angled triangle:
A right-angled triangle is a type of triangle that has one of its angles equal to 90 degrees.
The other two angles sum up to 90 degrees. The sides that include the right angle are perpendicular and the base of the triangle.
The third side is called the hypotenuse, which is the longest side of all three sides.
we know that,
According to pythagorean theorem:
\(AB^2+BC^2 = AC^2\)
3^2 + 4^2 = AC^2
9 + 16 = AC^2
AC^2 = 25
AC = \(\sqrt{25}\)
AC = 5 units.
Learn more about the length here:
https://brainly.com/question/2497593
#SPJ4
Full question:
is in the image uploaded

LEXI BOUGHT A NEW CAR. SHE DROVE 33 MILES IN THE FIRST
MONTH THAT SHE OWNED THE CAR AND 35 MILES IN THE
SECOND MONTH THAT SHE OWNED THE CAR. HOW MANY
MILES DID LEXI DRIVE IN ALL DYRING THE FIRST TWO
MONTHS THAT SHE OWNED THE CAR?
PLz helP iLL mArK brAinLYesT !*+
Answers
The spinner shown is spun twice. Express your answer
as a simplified fraction.
7. Find P(the two numbers have an even sum).
8. Find P(two even numbers).

Answers
7) The probability that the two numbers have an even sum is: 0.5
8) The probability that the two are even is: 0.25
How to find the probability in a spinner?7) We want to find the probability that the two numbers have an even sum.
The only combinations that produces an even sum are:
(1, 3), (3, 1), (1, 1), (2, 2), (2, 4), (4, 2), (4, 4), (3, 3)
The other combinations of numbers are:
(1, 2), (1, 4), (2, 1), (4, 1), (2, 3), (3, 2), (3, 4), (4, 3)
Thus, we have a total of 16 combinations and the probability that the two numbers have an even sum is:
P(two numbers with even sum) = 8/16 = 0.5
8) The probability that the two are even is:
4/16 = 1/4
= 0.25
Read more about spinner probability at: https://brainly.com/question/3765462
#SPJ1
)The mean voltage of a battery is 15 and S.D 0.2.Find the probability that four such batteries connected in series will have combined voltage of 60.8 or more volts
Answers
The probability that four batteries connected in series will have a combined voltage of 60.8 or more volts is approximately 0.0228 or 2.28%.
To find the probability that four batteries connected in series will have a combined voltage of 60.8 or more volts, we need to use the concept of the Central Limit Theorem.
In this case, we know that the mean voltage of a single battery is 15 volts and the standard deviation is 0.2 volts. When batteries are connected in series, their voltages add up.
The combined voltage of four batteries connected in series is the sum of their individual voltages. The mean of the combined voltage will be 4 times the mean of a single battery, which is 4 * 15 = 60 volts.
The standard deviation of the combined voltage will be the square root of the sum of the variances of the individual batteries. Since the batteries are connected in series, the variance of the combined voltage will be 4 times the variance of a single battery, which is 4 * (0.2)^2 = 0.16.
Now, we need to calculate the probability that the combined voltage of four batteries is 60.8 or more volts. We can use a standard normal distribution to calculate this probability.
First, we need to standardize the value of 60.8 using the formula:
Z = (X - μ) / σ
Where X is the value we want to standardize, μ is the mean, and σ is the standard deviation.
In this case, the standardized value is:
Z = (60.8 - 60) / sqrt(0.16)
Z = 0.8 / 0.4
Z = 2
Next, we can use a standard normal distribution table or calculator to find the probability associated with a Z-score of 2. The probability of obtaining a Z-score of 2 or more is approximately 0.0228.
Therefore, the probability that four batteries connected in series will have a combined voltage of 60.8 or more volts is approximately 0.0228 or 2.28%.
Learn more about probability here:
https://brainly.com/question/23417919
#SPJ8
2x+7y=11 is (-5,3) on the graph
Answers
Step-by-step explanation:
The given equation is :
2x+7y=11
We need to tell the point (-5,3) lies on the graph of the above equation of not.
Put x = -5 and y = 3 in the LHS of the above equation.
LHS = 2x+7y
= 2(-5)+7(3)
= -10 +21
= 11
It means, when we put x = -5 and y = 3 in the above equation, we get 11. Hence, (-5,3) lies on the graph of the equation.
Create a problem in which you add three different five digit numbers to get a sum of 93852
?+?+? =93,852
Answers
Answer:
50,000+30,000+13852=93,852
A model rocket is launched with an initial velocity of 250 ft per second. The height h, in feet, of the rocket t seconds after the launch is given by
h = −16t2 + 250t.
How many seconds after the launch will the rocket be 600 ft above the ground? Round to the nearest hundredth of a second. (Enter your answers as a comma-separated list.)
Answers
9514 1404 393
Answer:
{2.96, 12.66}
Step-by-step explanation:
A graph shows the rocket will be 600 feet up after 2.96 seconds, and again at 12.66 seconds.
__
You can solve the equation h = 600 to find the times.
-16t^2 +250t = 600
-16(t^2 -15.625t) = 600
-16(t^2 -15.625t +7.8125²) = 600 -16(7.8125²)
-16(t -7.8125)² = -376.5625
t -7.8125 = √(376.5625/16) ≈ ±4.8513
t = 7.8125 ± 4.8513 ≈ {2.9612, 12.6638}
The rocket will be 600 ft above the ground 2.96 and 12.66 seconds after launch.

a. p = 5t + 4
b. a = t2 - 4
c. d = t(5 – f)
Make t the subject in the formulas
Answers
Answer:
a, t = (p - 4)/5
b. t =√(a + 4)
c. t = d/(5-f)
Step-by-step explanation:
a. p = 5t + 4
To make t the subject of the equation, subtract 4 from both sides
p - 4 = 5t + 4 - 4
p - 4 = 5t
Divide both sides by 5
(p - 4)/5 = t
t = (p - 4)/5
b. a = t2 - 4
to make t the subject, add 4 to both sides
a + 4 = t2 - 4 + 4
a + 4 = t2
find the root of both sides
t =√(a + 4)
c. d = t(5 – f)
to make t the subject, divide both sides by 5 - f
d/(5-f) = t(5 – f)/(5 – f)
t = d/(5-f)
167.67 divided by 8.1
Answers
Answer:
167.67 divided by 8.1 = 20.7
simplify each algrebraic expression. drag tiles to correct boxes to complete the pairs.
-5x-2 5x+2 5x-2 -5x+2
Answers
(a) The algebraic expression, -5x - 2 + 5x + 2 is simplified as 0.
(b) The algebraic expression, 5x -2 - (5x + 2) is simplified as -4.
What is the simplification of the algebraic expression?The given algebraic expression is simplified by adding similar terms together, as it will make the expression to be in simplest form.
The given algebraic expressions are;
-5x - 2 + 5x + 2
5x -2 - (5x + 2)
The first algebraic expression is simplified as follows;
-5x - 2 + 5x + 2
collect similar terms;
(-5x + 5x) + (-2 + 2)
= 0 + 0
= 0
The second algebraic expression is simplified as follows;
5x - 2 - (5x + 2)
= 5x - 2 - 5x - 2
collect similar terms;
= (5x - 5x) + (-2 - 2)
= 0 - 4
= - 4
Learn more about simplification here: https://brainly.com/question/28008382
#SPJ1
An isosceles triangle whose sides are 5cm, 5cm and 6cm is inscribed in a circle. Find the radius of the circle.
Answers
Answer:
To find the radius of the circle inscribed in an isosceles triangle, we can use the following formula:
r = (a/2) * cot(π/n)
where r is the radius of the inscribed circle, a is the length of one of the equal sides of the isosceles triangle, and n is the number of sides of the polygon inscribed in the circle.
In this case, we have an isosceles triangle with two sides of 5cm and one side of 6cm. Since the triangle is isosceles, the angle opposite the 6cm side is bisected by the altitude and therefore, the two smaller angles are congruent. Let x be the measure of one of these angles. Using the Law of Cosines, we can solve for x:
6^2 = 5^2 + 5^2 - 2(5)(5)cos(x)
36 = 50 - 50cos(x)
cos(x) = (50 - 36)/50
cos(x) = 0.28
x = cos^-1(0.28) ≈ 73.7°
Since the isosceles triangle has two equal sides of length 5cm, we can divide the triangle into two congruent right triangles by drawing an altitude from the vertex opposite the 6cm side to the midpoint of the 6cm side. The length of this altitude can be found using the Pythagorean theorem:
(5/2)^2 + h^2 = 5^2
25/4 + h^2 = 25
h^2 = 75/4
h = sqrt(75)/2 = (5/2)sqrt(3)
Now we can find the radius of the inscribed circle using the formula:
r = (a/2) * cot(π/n)
where a = 5cm and n = 3 (since the circle is inscribed in a triangle, which is a 3-sided polygon). We can also use the fact that the distance from the center of the circle to the midpoint of each side of the triangle is equal to the radius of the circle. Therefore, the radius of the circle is equal to the altitude of the triangle from the vertex opposite the 6cm side:
r = (5/2) * cot(π/3) = (5/2) * sqrt(3) ≈ 2.89 cm
Therefore, the radius of the circle inscribed in the isosceles triangle with sides 5cm, 5cm, and 6cm is approximately 2.89 cm.
i need help solving #16 I have no idea how to do it

Answers
Answer:
d. 9x^2 + 25x + 14
Step-by-step explanation:
Formula of area of a rectangle is L * W;
L being length
W being width
x + 2 is our W
9x + 7 is our L, thus;
(x+2)(9x+7)
[9x^2 + 25x + 14]
Write the ratio for sin A.
sin A =
(Type an integer or a simplified fraction.)

Answers
The calculated ratio for the sine the angle A has its value to be 8/17
Writing the ratio for sin A.The ratio for sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse in a right triangle.
This ratio is commonly denoted as sin(θ), where θ is the angle of interest.
Mathematically, we can express this as:
sin(θ) = opposite / hypotenuse
Using the above, we have
opposite = 8
hypotenuse = 17
So, we have
sin(A) = 8/17
Hence, the ratio is 8/17
Read more about right triangles at
https://brainly.com/question/2437195
#SPJ1
please help me with this thank you

Answers
(9) The slope of a line perpendicular to the line, f(x) = 0.75x + 6 is - 4/3.
(10) The slope of a line parallel to this line, y = 10 -8x is -8.
What is the slope of a line perpendicular to the line?The slope of a line perpendicular to the line is the negative reciprocal of the slope of the line equation.
Question 9.
f(x) = 0.75x + 6
where;
0.75 is the slope of the line6 is the interceptThe slope of a line perpendicular to this line = -1/0.75 = -100/75 = -4/3
Question 10.
For the equation of another line, y = 10 - 8x
The slope of a line parallel to this line is equal to the slope of this line and it is calculated as follows;
y = 10 - 8x
where;
-8 is the slope10 is the y interceptslope of a line parallel to the line = -8
Learn more about slope of lines here: https://brainly.com/question/3493733
#SPJ1
Write the following absolute value function as a piecewise function.
f(x) = |- x² - 8x - 7|
Answers
The absolute value function as a piecewise function f(x) = |- x² - 8x - 7| is
f(x) = { - (x² + 8x + 7) , x ≤ -7 or x ≥ -1
{ x² + 8x + 7 , -7 < x < -1
What is meant by absolute value?
Absolute value is a mathematical function that gives the distance of a number from zero on a number line. It is denoted by two vertical bars enclosing the number and always returns a non-negative value.
What is meant by piecewise function?
A piecewise function is a function that is defined by different expressions or rules on different parts or intervals of its domain. The domain is divided into pieces, and each piece has its own expression or rule.
According to the given information
When x² + 8x + 7 ≥ 0, we have:
f(x) = |-(x² + 8x + 7)| = -(x² + 8x + 7)
When x² + 8x + 7 < 0, we have:
f(x) = |x² + 8x + 7| = x² + 8x + 7
To know more about absolute value visit:
brainly.com/question/1301718
#SPJ1
Please help me with this question! Please and Thank you❤️

Answers
Answer:
\( \frac{\pi}{4} = 45° \\ \\ \frac{\pi}{6} = 30°\)
\(( \cos( \frac{\pi}{4} ) + \sin( \frac{\pi}{6} ) ) ^{2} \\ \\ \\ {( \cos(45°) + \sin(30°) ) }^{2} \\ \\ \\ ( \frac{1}{ \sqrt{2} } + \frac{1}{2} ) ^{2} \\ \\ \\ (( \frac{1}{ \sqrt{2}} \times \frac{ \sqrt{2} }{ \sqrt{2}} ) + \frac{1}{2} )^{2} \\ \\ ( \frac{ \sqrt{2} }{2} + \frac{1}{2} )^{2} \\ \\ {( \frac{ \sqrt{2} + 1}{2} })^{2} \\ \\ \frac{( \sqrt{2} + 1)( \sqrt{2} + 1)}{ {2}^{2} } \\ \\ \\ \frac{2 + \sqrt{2} + \sqrt{2} + 1}{4} \\ \\ \\ = \frac{3 + 2 \sqrt{2} }{4} \\ \\ \\ = \frac{3 + 2(1.414)}{4} \\ \\ = \frac{3 + 2.828}{4} \\ \\ = \frac{5.828}{4} \\ \\ = 1.457\)
I hope I helped you^_^
What is the solution to |x-2| + 3 > 17?
Ox<-12 or x > 16
Ox<-14 or x>7
O-12
O-14
Answers
Answer:
x<-12 or x>16
Step-by-step explanation:
Answer:
|x - 2| + 3 > 17
|x - 2| > 14
x - 2 < -14 or x - 2 > 14
x < -12 or x > 16
What number is 10% less than 800
Answers
Answer:
720 (If you are counting 10% of 820, not 10% of 100)
Y = 800(1 - 0.1)
Y = 800(0.9)
Y = 720
Answer: \(720\)
Step-by-step explanation:
\(800-10%\)%
\(Y = 800(0.9)\)
Find the rate of change (slope) for the given table
a -1/4
b -4
c 1/4
d 4

Answers
65124 rounded to the nearest thousand
Answers
Answer:
65000 is the right answer, hope it helps ^w^
The graphs below show the number of faulty products, y, produced by a company for the first eight months since production started. Both graphs show the same information.
Answers
To support her discussion, it would be best for Alex to use Graph A for her presentation. Alex should use this graph for her presentation because the number of faulty products appears to decrease less on this graph.
What is a steeper slope?In Mathematics and Geometry, a steeper slope simply means that the slope of a line is bigger than the slope of another line. This ultimately implies that, a graph with a steeper slope has a greater (faster) rate of change in comparison with another graph.
In order to determine an equation with a declining line, we would have to determine the slope of each line graphically and then taking note of the line with a negative rate of change (slope) because it indicates a decreasing function.
In this context, we can reasonably infer and logically deduce that Graph A is more suited for Alex's presentation because the number of faulty products appears to decrease less on it.
Read more on slope here: brainly.com/question/3493733
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

perform the indicated operation (x-2)(x-11)
)
Answers
Answer:
x^2 - 22
Step-by-step explanation:
Answer:
x^2 - 13x + 22
Step-by-step explanation:
( x - 2 ) ( x - 11)
Start off with the first variable which is the “x”
Then multiply it by the variables in the other binomial
x * x = x^2
x * - 11 = -11x
Then take the -2 and do the same thing
-2 * x = -2x
-2 * -11 = 22
Now the the formula that you would have is: x^2 - 11x - 2x + 22
Simplify and your answer is:
x^2 - 13x + 22
What is the size of angle t in the image below? Give
your answer in degrees ().
t
340°
Answers
Reflex angle
Step-by-step explanation:
Reflex angle is more then 180 and less then 360
Answer:
yes buddy ans is reflex angle
a rectangle is four times a long as it is wide. if i has an area of 36 square inches, what are its dimensions?
Answers
Answer:
the dimensions are 3 sq in x 12 sq in
Step-by-step explanation:
12 divided by 3 is four (like the question said four times the width)
and then 3 times 12 is 36 sq in
sq in = square inches
