What is the relationship between sampling error and representation?
What is the purpose of the null hypothesis?
What are the criteria for a good hypothesis? (Hint: remember these criteria for application 3)
What is the relationship between ‘chance’ and our research hypothesis?
Why does the null hypothesis always refer to the population?
Multiple-Choice Questions:
6. The hypothesis helps to determine which of the following?
a. average score
b. variability
c. techniques to be used
d. sampling plan
7. The group you wish to generalize your results to is called the ______.
a. population
b. sample
c. sampling error
d. general group
8. Which of the following can be tested directly?
a. the null hypothesis
b. the research hypothesis
c. both the null and research hypotheses
d. all hypotheses
9. If there is no difference between sample and population values, what do you have?
a. a high sampling error
b. a low but positive sampling error
c. no sampling error
d. It cannot be determined.
10. Which of the following is a directional test?
a. a one-tailed test
b. a two-tailed test
c. the research hypothesis
d. the null hypothesis
11. Which of the following is a nondirectional test?
a. a one-tailed test
b. a two-tailed test
c. a research hypothesis
d. all hypotheses
12. If you were to hypothesize that communication students will have a higher average score on the oral communication measures, you would have a ______.
a. directional research hypothesis
b. nondirectional research hypothesis
c. null hypothesis
d. hypothesis type that cannot be determined
13. If you were to hypothesize that there is a relationship between reaction time and problem-solving ability, you would have a ______.
a. directional research hypothesis
b. nondirectional research hypothesis
c. null hypothesis
d. hypothesis type that cannot be determined
14. If you were to hypothesize that there is a positive relationship between reaction time and problem-solving ability, you would have a ______.
a. directional research hypothesis
b. nondirectional research hypothesis
c. null hypothesis
d. hypothesis type that cannot be determined
15. Which of the following represents a nondirectional research hypothesis?
a. H1: X1 < X2
b. H0: m1 = m2
c. H1: m1 > m2
d. H1: X1 ≠ X2
Answers
1. Sampling error refers to the discrepancy or difference between the characteristics of a sample and the characteristics of the population it represents. Representation, on the other hand, refers to the extent to which a sample accurately reflects the population. 2. The purpose of the null hypothesis is to serve as a basis for statistical hypothesis testing. It represents the assumption of no effect or no relationship in the population.
1. The criteria for a good hypothesis include being testable, specific, clear, and based on prior research or theoretical rationale. A good hypothesis should be formulated in a way that allows for empirical investigation and evaluation. It should provide a clear and concise statement about the expected relationship or difference between variables.
2. The research hypothesis is typically developed based on theoretical reasoning or prior empirical evidence. It represents the relationship or difference that the researcher is interested in investigating. The role of chance in relation to the research hypothesis is that statistical tests are used to determine the likelihood that the observed results are due to chance or reflect a true relationship. If the probability of obtaining the observed results by chance is low (below a predetermined threshold), it suggests support for the research hypothesis.
3. The null hypothesis always refers to the population because it represents the assumption that there is no effect or relationship in the population. Statistical hypothesis testing aims to make inferences about the population based on sample data. By comparing the sample data to the null hypothesis, researchers can evaluate whether the observed results are likely to occur due to chance or if they provide evidence to reject the null hypothesis and support the research hypothesis.
Multiple-Choice Questions:
6. c. techniques to be used
7. a. population
8. a. the null hypothesis
9. c. no sampling error
10. a. a one-tailed test
11. b. a two-tailed test
12. a. directional research hypothesis
13. b. nondirectional research hypothesis
14. a. directional research hypothesis
15. d. H1: X1 ≠ X2
Learn more about null hypothesis : brainly.com/question/31816995
#SPJ11
Related Questions
PLEASE ANSWER ASAP!! Georgia is a farmer and wants to plant a crop of tomato plants so she can sell her crop at the local farmer's market. She already has a large number of plants cultivated from last year's harvest. Each should produce an average of 35 tomatoes per plant during the growing season. She has found a nursery to buy more tomato plants at which are a different type. She found that these tomato plants will cost $5.25 each and should produce 25 tomatoes per plant on average over the course of the growing season. When planting, she wants to arrange the plants so that there are 5 fewer plants in each column than there are in each row. Georgia can spend no more than $500 on the tomato plants. In order to meet customer demands, she needs to produce at least 5,000 tomatoes during the growing season. Let x represent the number of plants in a row, and let y represent the number of plants that Georgia already has. Create a system of inequalities to find the number of plants in a row and the number of plants Georgia already has, and use it to determine how many of the solutions are viable.
A. Part of the solution region includes a negative number of tomato plants in a row; therefore, not all solutions are viable for the given situation.
B. There is no solution region.
C. None of the solution region is viable because there cannot be a negative number of tomato plants in a row and she can not have a negative number of tomato plants already on hand.
D. The entire solution region is viable.
Answers
Answer:
Part of the solution region includes a negative number of tomato plants in a row; therefore, not all solutions are viable for the given situation.
Step-by-step explanation:
got right on edmentum/plato
Suppose you have 18 cards, 11 spades (all different) and 7 hearts (all different). (a) How many ways are there to deal 5 cards from among the cards that you have? (b) If you deal 5 cards, what is the probability that 2 of them will be spades and 3 of them will be hearts? (c) If you deal 5 cards, what is the probability that you will deal more spades than hearts?
Answers
The number of ways to deal 5 cards from a set of 18 cards is 8568. The probability of getting 2 spades and 3 hearts when dealing 5 cards is approximately 22.49%. The probability of dealing more spades than hearts when dealing 5 cards is approximately 72.75%.
(a) The total number of ways to deal 5 cards from a set of 18 cards is given by the combination formula. We can choose 5 cards out of the 18 available cards in C(18, 5) ways. Therefore, there are C(18, 5) = 8568 ways to deal 5 cards from the given set.
(b) To calculate the probability of getting 2 spades and 3 hearts when dealing 5 cards, we need to consider the favorable outcomes (the number of ways to choose 2 spades and 3 hearts) and the total number of possible outcomes (the total number of ways to choose any 5 cards).
The number of ways to choose 2 spades out of 11 is C(11, 2) = 55, and the number of ways to choose 3 hearts out of 7 is C(7, 3) = 35. Since the events of choosing spades and hearts are independent, the total number of favorable outcomes is given by the product of these combinations: C(11, 2) * C(7, 3) = 55 * 35 = 1925.
The total number of possible outcomes is C(18, 5) = 8568, as calculated in part (a).
Therefore, the probability of getting 2 spades and 3 hearts when dealing 5 cards is P(2 spades and 3 hearts) = favorable outcomes / total outcomes = 1925 / 8568 ≈ 0.2249, or approximately 22.49%.
(c) To calculate the probability of dealing more spades than hearts, we need to consider the favorable outcomes where the number of spades dealt is greater than the number of hearts. This can be done by summing the probabilities of getting 3 spades and 2 hearts, 4 spades and 1 heart, and 5 spades and 0 hearts.
The number of ways to choose 3 spades out of 11 is C(11, 3) = 165, and the number of ways to choose 2 hearts out of 7 is C(7, 2) = 21. Therefore, the favorable outcomes for 3 spades and 2 hearts are given by C(11, 3) * C(7, 2) = 165 * 21 = 3465.
Similarly, the favorable outcomes for 4 spades and 1 heart are C(11, 4) * C(7, 1) = 330 * 7 = 2310, and for 5 spades and 0 hearts, it is C(11, 5) * C(7, 0) = 462.
The total number of favorable outcomes is the sum of these three cases: 3465 + 2310 + 462 = 6237.
Therefore, the probability of dealing more spades than hearts when dealing 5 cards is P(more spades than hearts) = favorable outcomes / total outcomes = 6237 / 8568 ≈ 0.7275, or approximately 72.75%.
Learn more about probability here:
brainly.com/question/31828911
#SPJ11
White shapes are black shapes are used in a game.
Some of the shapes are circles.
All the other shapes are squares.
The ratio of the number of white shapes to the number of black shapes is 7:3
The ratio of the number of white circles to the number of white squares is 2:7
The ratio of the number of black circles to the number of black squares is 1:2
Work out what fraction of all the shapes are circles.
Give your answer as a fraction in its simplest form.
Answers
——
White Circles 2:7 has a sum of 9.
2:7 = 2/7, where the 2 is circles.
2/9 = the ratio or amount of white circles of all white shapes.
Black Circles 1:2 has a sum of 3.
1:2 = 1/2, where the 1 is circles.
1/3 = the ratio or amount of black circles of all black shapes.
Now, back to the ratio of white to black shapes 7:3. Sum: 7+3=10 shapes.
7/10, where the 7 is white and 10 is black.
Multiply the total shapes by the circle ratios:
The total number of white circles of all the shapes is (2/9) x (7/10).
This simplifies to 2*7 / 9*10 = 14/90 (don’t simplify yet).
The total number of black circles of all the shapes is (1/3) x (3/10).
This simplifies to
1*3 / 3*10 = 3/30 (don’t simplify, instead multiply by 3 for the common denominator 90). (3/30) x 3 = 9/90.
Now we have 2 fractions; one for the white circles and black circles, respectively.
Add them together: 9/90 + 14/90 = 23/90.
This doesn’t simplify further, so the fraction of the shapes that is circles = 23/90.
Sandy and Sue each ha an amount of money between $0 and $1,000,000. The amount of money they each have i a non-zero poitive integer whole number. If Sue give X amount of money to Sandy, they will each both have an equal amount of money. If Sandy give that ame X amount of money to Sue, then Sue will have twice the amount of money a Sandy. If you take the numerical repreentation of Sue’ amount of money and take the firt leftmot digit and place that digit on the end of the numerical repreentation, that amount will be Sandy’ amount of money. (For example, if Sue ha $1234, then Sandy would have $2341). What i the amount of money Sue and Sandy have? What i the value of X?
Answers
Therefore , the solution to the given problem of equation comes out to be sue gives sandy $500000.
Explain the equation.A mathematical expression or language known as an equation is used to demonstrate the equality of two variables or mathematical expressions. noticing that the left and right weights are equal The equal sign is utilized to demonstrate the equality of two integers or mathematical equations. For instance, the equation for the aforementioned circumstance is 5 kg + 2 kg = 4 kg + 3 kg.
Here,
Given : Sandy and Sue each has an amount of money between $0 and $1,000,000.
thus,
Sue give X amount of money to Sandy, they will each both have an equal amount of money
then ,
X will be the amount given to sandy
=> 1000000 - x = 500000
=> x =500000
Therefore , the solution to the given problem of equation comes out to be sue gives sandy $500000.
To know more about equation , visit
brainly.com/question/10413253
#SPJ4
Question
(01.02 MC)
For which of the following distributions is the mean most likely to be less than the median?

Answers
The distribution where the mean is most likely to be less than the median is the third histogram.
How to illustrate the information?It should be noted that when the histogram shows the day is left skewed, it means the mean is less than the median.
If it right skewed, the mean is greater than the median.
When they're equal, the data is symmetric.
In this case, based on the information, the distribution where the mean is most likely to be less than the median is the third histogram.
Learn more about mean on:
brainly.com/question/1136789
#SPJ1
12c : 48c simplest form
Answers
Answer:
1 : 4
Step-by-step explanation:
12c : 48c ( divide both parts by 12c )
= 1 : 4
Answer:
1 and 4 so it would be 1:4
what’s the value of x ?

Answers
Here’s my work:

Round 1,234.805 to the nearest whole number
Answers
Answer:
1235
Step-by-step explanation:
Please brainliest
Answer:
the is 1235 hope this helps
Step-by-step explanation:
i need help it is overdue ):

Answers
Answer:
x = 4\(\sqrt{3}\) , y = 4
Step-by-step explanation:
using the cosine and sine ratios in the right triangle and the exact values
cos30° = \(\frac{\sqrt{3} }{2}\) , sin30° = \(\frac{1}{2}\) , then
cos30° = \(\frac{adjacent}{hypotenuse}\) = \(\frac{x}{8}\) = \(\frac{\sqrt{3} }{2}\) ( cross- multiply )
2x = 8\(\sqrt{3}\) ( divide both sides by 2 )
x = 4\(\sqrt{3}\)
and
sin30° = \(\frac{opposite}{hypotenuse}\) = \(\frac{y}{8}\) = \(\frac{1}{2}\) ( cross- multiply )
2y = 8 ( divide both sides by 2 )
y = 4
The slope of the line below is -3. Use the coordinates of the labeled point to
find a point-slope equation of the line.

Answers
Answer: y+7= 3(x-5) C
Step-by-step explanation:
7. What is the value of the postfix expression 6 3 2 4 + - *:
a) Something between -5 and -15
b) Something between 5 and -5
c) Something between 5 and 15
d) Something between 15 and 100
Answers
The value of the postfix expression 6 3 2 4 + - * is 18, which falls between 15 and 100. Therefore, the correct answer is d) Something between 15 and 100.
Here is the step-by-step of how to evaluate the postfix expression:
1. Start with the first two numbers, 6 and 3, and the first operator, *. Multiply 6 and 3 to get 18.
2. Move on to the next two numbers, 2 and 4, and the next operator, +. Add 2 and 4 to get 6.
3. Now you have 18 and 6, and the last operator, -. Subtract 6 from 18 to get 12.
4. The final result is 12.
Therefore, the value of the postfix expression 6 3 2 4 + - * is 12, which falls between 15 and 100. The correct answer is d) Something between 15 and 100.
Learn more about postfix
brainly.com/question/14294555
#SPJ11
y = negative 3 x minus 9 and y = one-third x minus 39 (9, –36) (9, 0) (–9, 18) (–9, –42)
Answers
Answer:A. (9, –36)
Step-by-step explanation:
A. (9, –36)
The Marked price of an article is rupees 4500. After allowing some percent of discount and levying 10% VAT it is sold at 4400, find discount percentage
Answers
Answer:
given,
mp= 4500
now
discount amount=dis%of mp
=x%of 4500
=45x
now,
sp=mp- discount
=4500-45x
now,
vat=vat%of SP
=10%*4500-45x
=450-45x
now,
sp with vat=sp+vat amount
=4500-45x+450-45x
=4950-90x
now,
4950-90x=4400
or,-90x=-550
or, x=55/9
or, x=6.11%
therefore, dis percent is 6.11%
9514 1404 393
Answer:
11.11%
Step-by-step explanation:
Let d represent the discount, as a fraction. Then the final price is ...
4500(1 -d)(1 +10%) = 4400
1 -d = 4400/(1.10·4500)
d = 1 - (4400/4950) = 0.111... ≈ 11.11%
The discount percentage is about 11.11%.
The drug warfarin, an anticoagulant, is metabolized by the body and leaves at a rate proportional to amount still in the body. Use this fact in both parts (a) and (b) below.
(a) If a patient, who has no Warfarin in his system, is given a pill containing 2.5 mg of Warfarin, write a differential equation for the quantity Q(t) (in mg) of warfarin in the body t hours later. Be sure to include an initial condition.
(b) A second patient, who has no Warfarin in her system, is given Warfarin intravenously at a rate of 0.5 mg/hour. Write a differential equation for the quantity Q(t) (in mg) of warfarin in the body of this patient t hours later. Be sure to include an initial condition.
*This is the problem, there is no more information provided.
These are my answers, just want to make sure they are right:
(a) Q' = -2.5Q Q(0) = 0
(b) Q' = 0.5Q - 2.5Q Q(0) = 0
Answers
The differential equation concerning the given question is Q' = -2.5Q Q(0) = 0 . Therefore the required correct answer for the question is Option A.
a) The differential equation expressing the quantity Q(t) of warfarin in the body, at t hours later when a patient who is suffering from Warfarin is given a pill containing 2.5 mg of Warfarin then,
dQ/dt = -kQ
here Q(0) = 2.5
b) The differential equation the expressing the quantity Q(t) of warfarin in the body, at t hours later when a patient who is not suffering from Warfarin is given a pill containing 0.5 mg/hr then,
dQ/dt = -kQ + r
where Q(0) = 0
Here
k = rate constant
r = rate of administration
The differential equation concerning the given question is Q' = -2.5Q Q(0) = 0 . Therefore the required correct answer for the question is Option A.
To learn more about differential equation,
https://brainly.com/question/1164377
#SPJ4
The rate at which Warfarin leaves the body should be proportional to the amount still in the body, not a constant rate of 2.5. So the correct differential equation for part (b) is:
Q' = 0.5 - kQ, where Q(0) = 0
Where k is the proportionality constant for the rate of elimination.
Explanation
(a) Let's denote the rate of elimination as k, where k > 0. Since the elimination rate is proportional to the amount of warfarin, we can write the differential equation as:
Q'(t) = -kQ(t)
Given that the initial condition is a 2.5 mg pill, the initial condition should be:
Q(0) = 2.5
So the differential equation for part (a) is:
Q'(t) = -kQ(t), Q(0) = 2.5
(b) In this case, the patient receives warfarin intravenously at a rate of 0.5 mg/hour. Thus, we should add the rate of administration to our equation:
Q'(t) = 0.5 - kQ(t)
The initial condition is still that the patient has no warfarin in her system:
Q(0) = 0
So the differential equation for part (b) is:
Q'(t) = 0.5 - kQ(t), Q(0) = 0
To learn more about differential equation : brainly.com/question/14620493
#SPJ11
I need help please each number has its own equation number it off please

Answers
5. x/8 - 5 > -6/10
6. 2 + x ≥ 4 * 12
Using diagonals from a common vertex, how many triangles could be formed from the polygon pictured below?

Answers
Using diagonals from a common vertex, the maximum number of triangles that will be formed is 5 triangles.
The given polygon is irregular heptagon (7 unequal sides).
The given polygon is irregular and the maximum number of triangles that will be Formed is explained as follows;
Choose one common vertex in the polygonDraw a diagonal line to meet other vertices from one common vertexThe maximum number of triangles that will be formed is 5Alternatively, we can use the following formula;
number of triangles formed = 7 - 2 = 5 triangles
Thus, using diagonals from a common vertex, the maximum number of triangles that will be formed is 5 triangles.
Learn more here:https://brainly.com/question/3700915
this one confuses me
focuses on pythagorean triples :)

Answers
Answer:
EH is 9 cm
DE is 18 cm
x is
18^2=9^2+b^2
b≈15,588
If A is an 2x 2 matrix and det (A)= -2, then det (-2A^-T)= 16. True or False?
Answers
\(det(-2A^(-T)) = -2\)and not 16, the statement "\(det(-2A^(-T)) = 16\)" is false.
Given that A is a 2x2 matrix and det(A) = -2, we want to find the determinant of \(-2A^(-T).\)
Find the determinant of \(A^(-T).\)
\(det(A^(-T)) = det((A^T)^-1) = 1/det(A^T) = 1/det(A) = 1/(-2) = -1/2.\)
Find the determinant of \(-2A^(-T).\)
To do this, we will use the property that
\(det(kB) = k^n × det(B)\)
where k is a scalar, n is the size of the matrix, and B is a matrix.
In our case, k = -2, n = 2 (as A is a 2x2 matrix), and B = A^(-T).
\(det(-2A^(-T)) = (-2)^2 × det(A^(-T)) = 4 × (-1/2) = -2.\)
Since \(det(-2A^(-T)) = -2\)and not 16, the statement "\(det(-2A^(-T)) = 16\)" is false.
for such more question on matrix
https://brainly.com/question/25581637
#SPJ11
15 is how many times larger than 5
Explain your answer in percent.
Answers
Answer:
3 times larger than 5
15.75%
I will give brainiest if you answer it and give a explanation.

Answers
Answer:
x = 35
Step-by-step explanation:
The angle marked 125° is angle DPE. The (vertical) angle formed from the rays opposite PD and PE is angle BPA. That angle is divided into two parts by ray PC. One of those parts is angle CPA, shown as 90°. The other part is angle CPB, shown as x°. This means ...
angle DPE = angle BPA . . . . vertical angles have the same measure
125° = 90° +x°
35 = x . . . . . . . . . . divide by °, subtract 90
hii can someone pls help, I’m not sure what the answer is
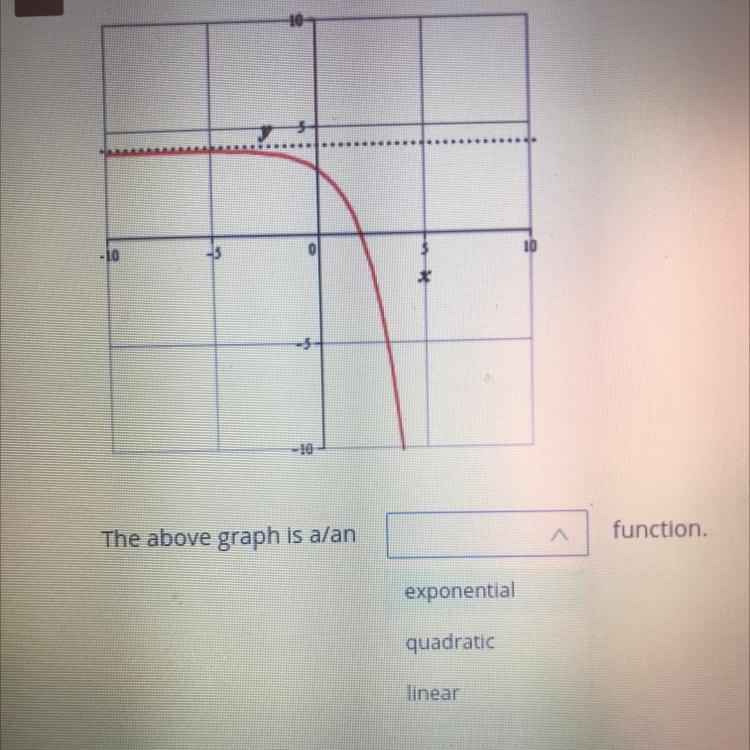
Answers
Answer:
i think its quadratic
Step-by-step explanation:
and form a right angle at their point of intersection, B.
If the coordinates of A and B are (14, -1) and (2, 1), respectively, the y-intercept of is
and the equation of is y =
x +
.
If the y-coordinate of point C is 13, its x-coordinate is
.
Answers
The y-intercept will be (0, 4/3). If the y-coordinate of point C is 13. Then the x-coordinate will be 4.
The complete question is given below.
AB and BC form a right angle at their point of intersection, B. If the coordinates of A and B are (14, -1) and (2, 1), respectively, the y-intercept of AB is ____ and the equation of BC is y = __ x + __. If the y-coordinate of point C is 13, its x-coordinate is ___.
What is the linear system?A linear system is one in which the parameter in the equation has a degree of one. It might have one, two, or even more variables.
The equation of the line passing through (14, -1) and (2, 1) will be
(y + 1) = [(1 + 1) / (2 - 14)] (x - 14)
y + 1 = -2/12(x - 14)
y + 1 = - 1/6 (x - 14)
Then the y-intercept of the equation will be
y + 1 = -1/6(-14)
y = 7/3 - 1
y = 4/3
The product of the perpendicular lines is a negative one.
Let m be the slope of the perpendicular line.
Then we have
(-1/6) m = -1
m = 6
Then the equation of the line will be
y = 6x + c
The equation is passing through point B (2, 1). Then we have
1 = 6(2) + c
c = -11
Then the equation will be
y = 6x - 11
If the y-coordinate of point C is 13. Then the x-coordinate will be
13 = 6x - 11
6x = 24
x = 4
More about the linear system link is given below.
https://brainly.com/question/20379472
#SPJ1

7/6 u = 42
how do i solve u
Answers
Answer:
36
Step-by-step explanation:
7/6 u=42
7u =42×6
u=252/7
u=36
SOMEONE HELP PLS, giving brainlist to anyone who answers

Answers
Answer:
\(s = \frac{3(1 - {6}^{9}) }{1 - 6} = 6046617\)
The sum of this finite geometric series is 6,046,617.
What is the product of 4 left-bracket cosine (StartFraction 2 pi Over 3 EndFraction) + I sine (StartFraction 2 pi Over 3 EndFraction) right-bracket and 2 left-bracket cosine (StartFraction pi Over 3 EndFraction) + I sine (StartFraction pi Over 3 EndFraction right-bracket?
Answer its D im just adding this for others to find
Answers
The required product of the function is \(8cos\frac{2\pi}{3}cos\frac{\pi}{3}+ 4i cos\frac{2\pi}{3}sin\frac{\pi}{3} + 2i sin\frac{2\pi}{3}cos\frac{\pi}{3} - 4i sin\frac{2\pi}{3}sin\frac{\pi}{3}\)
We are to find the product of the expression
\(a =4cos(\frac{2\pi}{3} )+isin(\frac{2\pi}{3})\\b=2cos(\frac{\pi}{3} )+isin(\frac{\pi}{3})\\\)
The product of the functions is expressed as;
\(ab = 4cos(\frac{2\pi}{3} )+isin(\frac{2\pi}{3})[2cos(\frac{\pi}{3} )+isin(\frac{\pi}{3}]\\ab=8cos\frac{2\pi}{3}cos\frac{\pi}{3}+ 4i cos\frac{2\pi}{3}sin\frac{\pi}{3} + 2i sin\frac{2\pi}{3}cos\frac{\pi}{3} + i^24i sin\frac{2\pi}{3}sin\frac{\pi}{3} \\ab=8cos\frac{2\pi}{3}cos\frac{\pi}{3}+ 4i cos\frac{2\pi}{3}sin\frac{\pi}{3} + 2i sin\frac{2\pi}{3}cos\frac{\pi}{3} - 4i sin\frac{2\pi}{3}sin\frac{\pi}{3}\)
Note that i² = -1
Hence the required product of the function is \(8cos\frac{2\pi}{3}cos\frac{\pi}{3}+ 4i cos\frac{2\pi}{3}sin\frac{\pi}{3} + 2i sin\frac{2\pi}{3}cos\frac{\pi}{3} - 4i sin\frac{2\pi}{3}sin\frac{\pi}{3}\)
Learn more here: https://brainly.com/question/9258225
Answer:
D\(8[cos(\pi )+i sin(\pi )}\)
Step-by-step explanation:
A club consists of 5 girls (Kirsten, Sarah, Suzie, Monica, and Katie) and 3 boys (Kevin, Steve and Samuel). Find P(Girl | K-name)
Answer:
2/3
Answers
The total probability of a girl having a "K-name" is 3/8. The total probability of there being a girl in the club is 5/8.
Therefore, the conditional probability of having a girl with a "K-name" given that there is a girl in the club can be calculated as follows:
P (Girl | K-name) = P (K-name | Girl) × P (Girl) / P (K-name) = 2/5 * 5/8 / 3/8 = 2/3
Therefore, the probability of a girl with a K-name given that there is a girl in the club is 2/3.
In a club consisting of 5 girls (Kirsten, Sarah, Suzie, Monica, and Katie) and 3 boys (Kevin, Steve, and Samuel), we are asked to find P(Girl | K-name).
We can use Bayes' theorem to calculate the conditional probability of this event. This theorem states that the probability of an event given another event can be calculated as the product of the probability of the second event Therefore, the probability of a girl having a "K-name" given that there is a girl in the club is 2/3.
The conditional probability of there being a girl in the club given that a girl has a K-name is 2/3.
To know more about conditional probability visit:
brainly.com/question/10567654
#SPJ11
Explain whether the table represents a function

Answers
Answer:
Yes
Step-by-step explanation:
Because for every x value there is only one y value
What shape best describes the cross section cut parallel to the base of a right rectangular prism?
Rectangle
Parallelogram
Square
Trapezoid

Answers
Answer:
rectangle
Step-by-step explanation:
She selects 150 trees at random from her orchard and uses this fertilizer on those trees and estimates the following regression: Y
^
i
=600+4.93X i
, where Y
^
i
denotes the predicted number of apricots obtained from the I th tree and X i
denotes the number of units of fertilizer used on the I th tree. A. H 0
:β 1
≥5.14 and H 1
:β 1
<5.14. B. H 0
:β 1
>4.93 and H 1
:β 1
≤4.93. C. H 0
:β 1
=5.14 and H 1
:β 1
=5.14. D. H 0
:β 0
=4.93 and H 1
:β 0
=4.93. Suppose the standard error of the estimated slope is 0.74. The t-statistic associated with the test Wendy wishes to conduct is (Round your answer to two decimal places. Enter a minus sign if your answer is negative.1
Answers
Given statement solution is :- The t-statistic associated with the test is approximately -0.28.
The t-statistic, which is used in statistics, measures how far a parameter's estimated value deviates from its hypothesised value relative to its standard error. Through the Student's t-test, it is utilised in hypothesis testing. In a t-test, the t-statistic is used to decide whether to accept or reject the null hypothesis.
To find the t-statistic associated with the test, we need to calculate the test statistic using the estimated slope coefficient, the null hypothesis, and the standard error.
The estimated slope coefficient is 4.93.
The null hypothesis is H₀: β₁ ≥ 5.14 (stating that the true slope coefficient is greater than or equal to 5.14).
The predicted slope's standard error is 0.74.
The formula to calculate the t-statistic is:
t = (estimated slope - hypothesized slope) / standard error
Plugging in the values:
t = (4.93 - 5.14) / 0.74
t = -0.21 / 0.74
t ≈ -0.28 (rounded to two decimal places)
Therefore, the t-statistic associated with the test is approximately -0.28.
For such more questions on t-statistic
https://brainly.com/question/28235817
#SPJ8
Let X and Y be independent Bernoulli random variables, and assume that X has success probability p and Y has success probability q, where 0 < p, q < 1. Determine the cumulative distribution functions (CDFs) and probability mass functions (PMFs) of Z = max{X,Y } and V = min{X,Y }. Make sure to completely specify these functions. What kinds of distributions do Z and V have?
Answers
The PMF of V can be found by taking the difference of the CDF values:
P_V(v) = F_V(v) - F_V(v-1) = { (1-p)(1-q) for v = 0, pq - (1-p)(1-q) for v = 1 }.
To find the CDF of Z = max{X,Y}, we note that Z = 1 if and only if at least one of X and Y is 1. Since X and Y are independent, we have:
P(Z = 1) = P(X = 1 or Y = 1) = P(X = 1) + P(Y = 1) - P(X = 1 and Y = 1)
= p + q - pq
Similarly, P(Z = 0) = P(X = 0 and Y = 0) = (1-p)(1-q). Therefore, the CDF of Z is given by:
F_Z(z) = P(Z ≤ z) = { 0 for z < 0,
(1-p)(1-q) for 0 ≤ z < 1,
p + q - pq for z ≥ 1 }
The PMF of Z can be found by taking the difference of the CDF values:
P_Z(z) = F_Z(z) - F_Z(z-1) = { (1-p)(1-q) for z = 0,
p + q - pq - (1-p)(1-q) for z = 1 }
Similarly, to find the CDF and PMF of V = min{X,Y}, note that V = 0 if and only if both X and Y are 0. We have:
P(V = 0) = P(X = 0 and Y = 0) = (1-p)(1-q)
Similarly, P(V = 1) = P(X = 1 and Y = 0 or X = 0 and Y = 1) = 2pq - pq = pq.
Therefore, the CDF of V is given by:
F_V(v) = P(V ≤ v) = { 0 for v < 0,
(1-p)(1-q) for 0 ≤ v < 1,
1 - pq for v ≥ 1 }
The PMF of V can be found by taking the difference of the CDF values:
P_V(v) = F_V(v) - F_V(v-1) = { (1-p)(1-q) for v = 0,
pq - (1-p)(1-q) for v = 1 }
The distribution of Z is known as a Bernoulli mixture distribution, while the distribution of V is known as a geometric mixture distribution.
Learn more about CDF here
https://brainly.com/question/30697050
#SPJ11