What is the point slope of a line that has a slope of three and passes through the .1, four

Answers
Answer:
1st option
Step-by-step explanation:
The equation of a line in point- slope form is
y - y₁ = m(x - x₁ )
where m is the slope and (x₁, y₁ ) a point on the line
Here m = 3 and (x₁, y₁ ) = (1, 4 ) , then
y - 4 = 3(x - 1)
Related Questions
Which set of ordered pairs has the same slope as the given set: (0,10) (4, -4)?
Answers
The set of ordered pairs which has the same slope as the given set is (0,7) (2, 0).
Which set of ordered pairs has the same slope as the given set: (0,10) (4, -4)?The slope is defined as the ratio of the vertical change between two points, the rise, to the horizontal change between the same two points, the run.
Mathematically, the slope is the change in y divided by the change in x. That is:
Slope = (y₂-y₁) / (x₂-x₁)
For the given set: (0,10), (4, -4):
(0,10): x₁ = 0, y₁ = 10
(4, -4): x₂ = 4, y₂ = -4
Slope = (-4 -10) / (4-0)
= -14/4
= -3.5
Let's check which set of ordered pairs has the same slope as the given set: (0,10) (4, -4):
For (-1, -1) (3,1):
Slope = (1 -(-1)) / (3-(-1)) = 0.5
For (8,2) (1,2):
Slope = (2-2) / (1-8) = 0
For (0,7) (2, 0):
Slope = (0-7) / (2-0) = -3.5
For (9, 10) (3, 4):
Slope = (4-10) / (3-9) = 1
Therefore, the set of ordered pairs which has the same slope as the given set is (0,7) (2, 0).
Learn more about slope on:
brainly.com/question/5192230
#SPJ1
Complete Question
See image attached

Justin divided 403 by a number and got a quotient of 26 with a remainder of 13. What was the number Justin divided by
Answers
( 403 + 13 ) ÷ 26
= 416 ÷ 26
= 16
Problem 5 (10 pts) Let X = U(4) out of 8 standard ordered uniforms and Y uniforms. U5) out of 8 standard ordered 1. (5 pts) Derive the joint density fx,y(x, y). 2. (5 pts) Evaluate P(Y < +X). Hint: it might be easier to find the distribution of Y - X
Answers
The problem involves finding the joint density function and the probability of Y being less than X for two uniform distributions, X and Y
To find the joint density function fx,y(x,y), we can use the fact that for independent continuous random variables, the joint density function is the product of the individual density functions. Here, X and Y are independent and uniformly distributed over [0,1], so their individual density functions are fX(x) = 1 for 0 ≤ x ≤ 1 and fY(y) = 1 for 0 ≤ y ≤ 1. Therefore, the joint density function is fx,y(x,y) = fX(x) * fY(y) = 1 for 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1.
To find the probability P(Y < X), we can use the fact that the difference of two independent uniform distributions is a triangular distribution. Specifically, if Z = Y - X, then Z is uniformly distributed over [-1,1]. Therefore, P(Y < X) = P(Y - X < 0) = P(Z < 0) = 0.5, since the probability that Z is negative is equal to the probability that it is positive, and both add up to 1. Alternatively, we can integrate the joint density function over the region where y < x:
P(Y < X) = ∫∫[y<x]fx,y(x,y)dxdy = ∫0^1∫0^y 1 \(dxdy\) + ∫0^1∫y^1 1 dxdy = 0.5
where [y<x] is the indicator function that is equal to 1 if y < x and 0 otherwise. Thus, the probability that Y is less than X is 0.5
Learn more about uniform distribution here:
https://brainly.com/question/30639872
#SPJ11
A stable second-order process may be destabilized by using a PI controller" - comment on this statement by considering the stability (to be determined using, say, Routh Test) for a system with Gp = 1/[s+2s+2] . (The remaining elements are all unity gain with no dynamics)
Answers
based on the Routh-Hurwitz stability criterion, the system with Gp = 1/[s+2s+2] is stable.
To analyze the stability of the system with Gp = 1/[s+2s+2], we can use the Routh-Hurwitz stability criterion. The Routh-Hurwitz criterion provides a method to determine the stability of a system based on the coefficients of its characteristic equation.
The characteristic equation of the system can be obtained by setting the denominator of Gp equal to zero:
s^2 + 2s + 2 = 0
Using the Routh-Hurwitz criterion, we construct the Routh array:
s^2 | 1 2
s^1 | 2
s^0 | 2
To apply the Routh-Hurwitz criterion, we need to check for sign changes in the first column of the Routh array. If there are no sign changes, the system is stable. If there are sign changes, the system may be unstable.
In this case, we can see that there are no sign changes in the first column of the Routh array. All the elements are positive or zero. This indicates that all the poles of the system have negative real parts, which implies stability.
Therefore, based on the Routh-Hurwitz stability criterion, the system with Gp = 1/[s+2s+2] is stable.
To know more about Routh-Hurwitz stability
https://brainly.com/question/31479909
#SPJ11
A city has cone-shaped buildings for storing salt and sand for icy roads. Each
building has a radius of 25 feet and a height of 18 feet. Find the volume of the
building. Use 3.14 for TT.
OA. 35,325 ft3
OB. 11,775 ft3
OC. 471 ft3
OD. 1413 ft3

Answers
The volume of the building is, 11,775 ft³
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
A city has cone-shaped buildings for storing salt and sand for icy roads. Each building has a radius of 25 feet and a height of 18 feet.
Now, We know that;
⇒ Volume of Cone = πr²h/3
Here, Each building has a radius of 25 feet and a height of 18 feet.
Hence, Volume of building is,
⇒ V = πr²h/3
⇒ V = 3.14 × 25² × 18 / 3
⇒ V = 11,775 ft³
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
In your reservoir, you have a production well which flows for 48 hours at 200 STB/day, and then shut-in for 24 hours. The following additional data are given : Pi = 3100 psi Ct = 15x10^-6 psi^-1 Bo = 1.3 bbl/STB ϕ = 15% μ=1.2 cp K = 45 md and h = 60 ft
a-) Calculate the pressure in this production well at 12 hours of shut in
b-) Explain how can you use superposition in time to analyze a pressure build-up test.
Answers
a) To calculate the pressure at 12 hours of shut-in:
substitute the given values into the pressure buildup equation and solve for P(t=12).
b) Superposition in time is used in pressure buildup analysis by adding or summing the responses of multiple transient tests to analyze and interpret reservoir behavior and properties.
We have,
a) To calculate the pressure in the production well at 12 hours of a shut-in, we can use the equation for pressure transient analysis during shut-in periods, known as the pressure buildup equation:
P(t) = Pi + (Q / (4πKh)) * log((0.14ϕμCt(t + Δt)) / (Bo(ΔP + Δt)))
Where:
P(t) = Pressure at time t
Pi = Initial reservoir pressure
Q = Flow rate
K = Permeability
h = Reservoir thickness
ϕ = Porosity
μ = Viscosity
Ct = Total compressibility
t = Shut-in time (12 hours)
Δt = Time since the start of the flow period
Bo = Oil formation volume factor
ΔP = Pressure drop during the flow period
Given:
Pi = 3100 psi
Q = 200 STB/day
K = 45 md
h = 60 ft
ϕ = 15%
μ = 1.2 cp
Ct = 15x10^-6 psi^-1
Bo = 1.3 bbl/STB
t = 12 hours
Δt = 48 hours
ΔP = Pi - P(t=Δt) = Pi - (Q / (4πKh)) * log((0.14ϕμCt(Δt + Δt)) / (Bo(ΔP + Δt)))
Substituting the given values into the equation:
ΔP = 3100 - (200 / (4π * 45 * 60)) * log((0.14 * 0.15 * 1.2 * 15x\(10^{-6}\) * (48 + 48)) / (1.3 * (3100 - (200 / (4π * 45 * 60)) * log((0.14 * 0.15 * 1.2 * 15 x \(10^{-6}\) * (48 + 48)) / (1.3 * (0 + 48))))))
After evaluating the equation, we can find the pressure in the production well at 12 hours of shut-in.
b) Superposition in time is a principle used in pressure transient analysis to analyze and interpret pressure build-up tests.
It involves adding or superimposing the responses of multiple transient tests to simulate the pressure behavior of a reservoir.
The principle of superposition states that the response of a reservoir to a series of pressure changes is the sum of the individual responses to each change.
Superposition allows us to combine the information obtained from multiple tests and obtain a more comprehensive understanding of the reservoir's behavior and properties.
It is a powerful technique used in reservoir engineering to optimize production strategies and make informed decisions regarding reservoir management.
Thus,
a) To calculate the pressure at 12 hours of shut-in:
substitute the given values into the pressure buildup equation and solve for P(t=12).
b) Superposition in time is used in pressure buildup analysis by adding or summing the responses of multiple transient tests to analyze and interpret reservoir behavior and properties.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ12
a scientist claims that 9% of viruses are airborne. if the scientist is accurate, what is the probability that the proportion of airborne viruses in a sample of 596 viruses would differ from the population proportion by greater than 3%? round your answer to four decimal places.
Answers
The probability that the sample proportion of airborne viruses in differ from the population proportion by greater than 3% is 0.006.
According to the Central limit theorem, if from an unknown population large samples of sizes n > 30, are selected and the sample proportion for each sample is computed then the sampling distribution of sample proportion follows a Normal distribution.
The information provided is:
n = 596
p = 0.09
The mean and standard deviation are:
Compute the probability that the sample proportion of airborne viruses in differ from the population proportion by greater than 3% as follows
Hence, the probability that the sample proportion of airborne viruses in differ from the population proportion by greater than 3% is 0.006.
Learn more about Probability here https://brainly.com/question/13604758
#SPJ4
Bearing a to b is 280 what is bearing b to A
Answers
Answer:
please see photo attached for detailed analysis.

Fill in the blank to make an equivalent ratio.
4:7 = ______ : 56
Answers
Answer:
4:7 = 32:56
Step-by-step explanation:
4 x 8 = 32
7 x 8 = 36
Hope this helped!
PLZZZZZ give me brainliest
Answer: 32:56
Step-by-step explanation:
because first I divided 56/7=8 and then did 4*8=32. You're welcome!!! c:
Someone help please

Answers
The measure of the angles that is supplementary to the given angles is as follows:
4. 52°
5. 20°
6. 130°
How to find supplementary angles?Supplementary angles are those angles that sum up to 180 degrees. In
other words, supplementary angles refer to the pair of angles that always
sum up to 180°. Therefore, let's find the measure of the angles that are
supplementary angles to the following angles.
Therefore,
4.
180 - 128 = 52 degrees
5.
180 - 160 = 20 degrees
6.
180 - 50 = 130 degrees
learn more on supplementary angles here:https://brainly.com/question/18362240
#SPJ1
Determine whether the series is convergent or divergent.
[infinity]n7
n16 + 1
n = 1
O convergent
O divergent
Answers
The series is ∑ \(\frac{1}{n^5}\) from n=1 to infinity which is convergent.
What is integral test for convergence or divergence?In mathematics, the integral test for convergence is a method used to test infinite series of monotonous terms for convergence.
The Integral Test says that if \(a_n > 0\) is a sequence and f(x) > 0 is monotonic decrescent and \(a_n=f(n)\) ∀ n
\(\int\limits^\infty_1 f{x} \, dx \\\\\) exists finite ⇔ ∑(infinity to n = 1) \(a_n\) converges
We know:
\(\int\limits^\infty_1 {\frac{1}{x^5} } \, dx =(-\frac{1}{4x^4} )^\infty_1=\frac{1}{4}\)
which is finite, so the series converges.
Learn more about Integral test at:
https://brainly.com/question/28157842
#SPJ4
The given question is incorrect, correct question is:
Use the Integral Test to determine whether the series is convergent or divergent given ∑ \(\frac{1}{n^5}\) from n=1 to infinity?
Please help for brainliest, thanks.

Answers
Answer:
above
Step-by-step explanation:
1 is the nearest whole number
If you answer this question you get brainliest
Answers
I don't see the question, so...
Disprove: If a and b are nonnegative integers with a|b, then a ≤ b.
Note: A counterexample to this statement would also be a counterexample for the previous problem, but not necessarily vice versa.
Answers
This statement is true. However, a counterexample to the given statement (If a and b are nonnegative integers with a|b, then a ≤ b) can also be used as a counterexample for the previous statement, but the reverse is not true.
The given statement is Disprove: If a and b are nonnegative integers with a| b, then a ≤ b. Note: A counterexample to this statement would also be a counterexample for the previous problem, but not necessarily vice versa. To disprove this statement, we need to present a counterexample. Here is the counter example:
Let's take a = 4 and b = 2Since 2 | 4, a| b, and both are nonnegative integers. But, a is not less than or equal to b i.e., 4 is not less than or equal to 2. Therefore, the statement is false.
A counterexample to this statement would also be a counterexample for the previous problem, but not necessarily vice versa. The previous problem is a statement in the opposite direction. It says that "If a and b are nonnegative integers with a ≤ b, then a| b."
This statement is true. However, a counterexample to the given statement (If a and b are nonnegative integers with a| b, then a ≤ b) can also be used as a counterexample for the previous statement, but the reverse is not true.
to know more about nonnegative integers visit :
https://brainly.com/question/30433131
#SPJ11
Beginning with a regular hexagon, a 6-pointed star is formed by constructing equilateral triangles, whose sides are the same length as the sides of the hexagon, on each side of the hexagon as shown. One of the equilateral triangles is shaded. The shaded area is what fractional part of the entire area of the 6-pointed star? Express the answer as a fraction in simplest form.
Answers
Answer:
1/12
Step-by-step explanation:
a graphical tool used to help determine whether a process is in control or out of control is a
Answers
A graphical tool used to help determine whether a process is in control or out of control is known as a Control Chart.
Control charts are essential in quality control and statistical process control (SPC). They allow you to monitor process performance and variability over time, enabling you to identify trends, shifts, or deviations from the established process baseline.
Control charts typically consist of a centerline, representing the process mean, and upper and lower control limits, which indicate the acceptable range of variation. Data points are plotted on the chart, and if they fall within the control limits, the process is considered to be in control. If data points fall outside the control limits or display non-random patterns, the process is considered out of control, signaling potential issues that need to be investigated and addressed.
In summary, control charts are a valuable graphical tool that assists in determining the stability of a process, facilitating continuous improvement efforts and ensuring product quality. They provide a visual representation of process variation and help identify when corrective actions are needed to bring a process back into control.
To learn more about charts click here
brainly.com/question/30387848
#SPJ11
Which statements are true regarding the prism? Check
all that apply.
The prism has no vertices.
The prism has 9 edges.
The bases of the prism are triangles.
The bases of the prism are rectangles.
The prism has 5 faces.
Answers
Answer:
The prism has 9 edges, The bases of the prism are triangles, and the prism has 5 faces.
Would really appreciate a brainliest! Hope this helped! =)
Answer: B, C, E
Step-by-step explanation: dude trust me c'mon
Can someone please solve for me

Answers
Let x = 0.263263263…
Then 1000x = 263.263263263…
Subtracting x gives
1000x - x = 263.263263263… - 0.263263263…
999x = 263
x = 263/999
please help again forgot everything

Answers
Answer:
a
Step-by-step explanation:
to find a proportion they must equal each other
8/4 in its simplest form is just 2
to make r/3 = 2 r must be 6
6/3 is 2
Cual es el resultado de 5+3-4+(6x7)-(18:3)=
Answers
Step-by-step explanation:
Assume that from past experience with the satisfaction rating score, a population standard deviation of σ≦12 is expected. In 2012 , Costco, with its 432 warehouses in 40 states, was the only chain store to earn an outstanding rating for overall quality (Consumer Reports, 03/2012). Now, a sample of 11 Costco customer satisfaction scores provided the sample mean =84 and the sample standard deviation =11.3. Construct a hypothesis test to determine whether the population standard deviation of σ≦12 should be rejected for Costco. Also, a 0.05 level of significance is used (i.e., α=0.05 )
Answers
it can be concluded that the population standard deviation is within or less than 12.
To construct a hypothesis test to determine whether the population standard deviation of σ≦12 should be rejected for Costco, we can use a chi-square test for variance.
Step 1: State the null and alternative hypotheses:
- Null hypothesis (H₀): σ ≤ 12
- Alternative hypothesis (H₁): σ > 12
Step 2: Determine the level of significance (α = 0.05) and degrees of freedom (df = n - 1 = 11 - 1 = 10).
Step 3: Calculate the test statistic:
- χ² = (n - 1) * (s² / σ²) = 10 * (11.3² / 12²) = 10 * 0.94 = 9.4
Step 4: Determine the critical value:
- The critical value at α = 0.05 with df = 10 is χ²ₐ = 18.307
Step 5: Compare the test statistic with the critical value:
- Since χ² = 9.4 < χ²ₐ = 18.307, we fail to reject the null hypothesis.
Step 6: Conclusion:
- Based on the given sample data, there is not enough evidence to reject the hypothesis that the population standard deviation of σ≤12 for Costco.
Therefore, it can be concluded that the population standard deviation is within or less than 12.
Learn more about hypothesis from the following link:
https://brainly.com/question/606806
#SPJ11
find the length of the diagonal of a 7cmx6cmx12cm rectangular prism. round to the nearest tenth.
Answers
Answer:
9.4 cm to nearest tenth.
Step-by-step explanation:
Diagonal of the 6*2 base:
d^2 = 6^2 + 2^2 = 40
d = √40
So the required diagonal:
D^2 = (√40)^2+ 7^2
D^2 = 89
D = √89 = 9.434.
Answer:
15.1
Step-by-step explanation:
To find the length of the rectangular prism' diagonal, use the formula for the length of a diagonal of a right rectangular prism.
d=l2+w2+h2−−−−√
Substitute 7 for l, 6 for w, and 12 for h
Then simplify.
d=72+62+122−−−−√
=49+36+144−−−−√
=229−−−√≈15.1
Therefore, the length of the rectangular prism's diagonal is about 15.1cm.
Which of the following pairs consists of equivalent fractions?
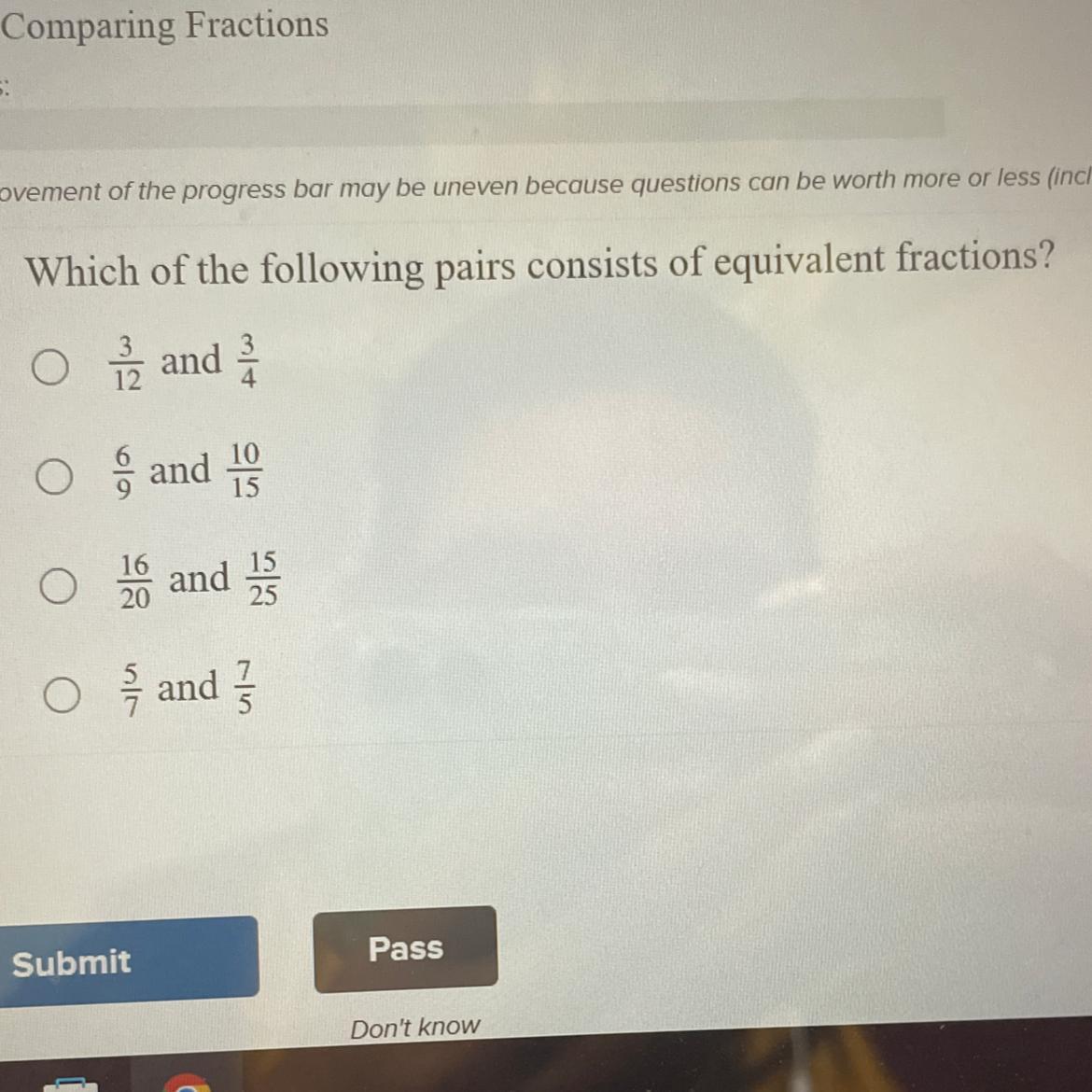
Answers
Answer:
the second pair
Step-by-step explanation:
the first pair can't be equivalent because to check whether two fractions are equivalent we have to use the criss-cross method so.....
1.3*4=12 and 12*3=36....so not equal
2.6*15=90 and 9*10=90.....it matches:)) so this is the answer
Can anyone help me with this!

Answers
A. The approximate value of the y-intercept is 48.
B. The approximate slope of the line is 2.76.
C. The expected number of cones of ice cream sold when the temperature is 30 °C is approximately 83.
To determine the line of best fit for the given data, we can use linear regression analysis. Linear regression helps us find the equation of a line that best represents the relationship between the temperature and the cones of ice cream sold.
A. To find the approximate value of the y-intercept (the point where the line intersects the y-axis), we can use the linear regression equation. In this case, the y-intercept represents the expected number of cones of ice cream sold when the temperature is 0 °C. From the given data, we do not have a data point at 0 °C. However, we can still estimate the y-intercept using the regression line. The approximate value of the y-intercept is around 48 (rounded to the nearest whole number).
B. To find the approximate slope of the line, we can use the linear regression equation. The slope represents the change in the number of cones of ice cream sold for a one-unit increase in temperature. From the linear regression analysis, the approximate slope of the line is around 2.76 (rounded to two decimal places).
C. To find the expected number of cones of ice cream sold when the temperature is 30 °C, we can substitute the temperature value into the regression equation. Using the approximate slope and y-intercept values from above, we can calculate the expected number of cones sold:
Expected number of cones sold = (slope x temperature) + y-intercept
Expected number of cones sold = (2.76 * 30) + 48
Expected number of cones sold ≈ 82.8 (rounded to the nearest whole number).
To learn more about the line of the best fit;
https://brainly.com/question/14279419
#SPJ1
GIVING BRAINLIEST:
The Bayview Community Pool has a snack stand where Juan works part-time. He tracked his total sales during each shift last month. This box plot shows the results. What fraction of Juan's shifts had total sales of $225 or more?

Answers
1/4 or 25% of Juan's shifts had total sales of $225 or more.
We have,
To determine the fraction of Juan's shifts that had total sales of $225 or more, we need to analyze the given box plot.
From the box plot, we know that the median (Q2) is 200, the first quartile (Q1) is 150, and the third quartile (Q3) is 225.
The lowest value is 100, and the largest value is 275.
Since the third quartile (Q3) represents the value below which 75% of the data falls, and it is equal to 225 in this case, we can say that 75% of Juan's shifts had total sales of less than $225.
So,
The fraction of Juan's shifts with total sales of $225 or more is 1 - 0.75, which is equal to 0.25 or 1/4.
Thus,
1/4 or 25% of Juan's shifts had total sales of $225 or more.
Learn more about box plots here:
https://brainly.com/question/9827993
#SPJ1
one angle of a right angled triangle is 63degree .find the other angle in grades
Answers
Answer:
27°
Step-by-step explanation:
The sum of the 3 angles in a triangle = 180°
let the third angle be x , then
x + 90° + 63° = 180°
x + 153° = 180° ( subtract 153° from both sides )
x = 27°
Answer:
27 degrees
Step-by-step explanation:
A right angled triangle has 1 angle as 90 degree. And as you know the other angle is 63 degree, and the angle sum property of a triangle is 180 degrees. So-
Let's take 'x' as the other angle.
90 + 63 + x = 180
153 + x = 180
x = 180 - 153 = 27
x = 27 degrees
So, the other angle is 27 degrees.
All the angles of the right-angled triangle are- 90, 63, 27.
freeeeeeeeeeee33eeeeeeeeeeeee POINTSSSSSS
Answers
thanks 4 the points lolllll
Answer:
someone deleted my answer, but thank you again.
Step-by-step explanation:
1. If we are told that (x+4)(x+7)=0, then what can we infer?
By zero product property we know: __ = 0 OR __ = 0
And therefore we know that X=__ OR X= ___
2. If we are told that (3x-7)(2x+5)=0 then what can we infer?
By zero product property we know: __ = 0 OR __ = 0
And therefore we know that X=__ OR X= ___
3.We want to solve the equation x^2-3x-40=0
First factor x^2-3x-40: ___
By zero product property we know: __ = 0 OR __ = 0
And therefore we know that X=__ OR X= ___
4.We want to solve the equation 3x^2-11x-42=0
First factor 3x^2-11x-42: ___
By zero product property we know: __ = 0 OR __ = 0
And therefore we know that X=__ OR X= ___
5.We want to solve the equation 10x^2+9x+2=0
First factor 10x^2+9x+2
By zero product property we know: __ = 0 OR __ = 0
And therefore we know that X=__ OR X= ___
Answers
1. x + 4 = 0 or x + 7 = 0
x = -4 or x = -7
2. 3x - 7 = 0 or 2x + 5 = 0
x = 7/ 3 or x = -5/ 2
3. x + 5 = 0 or x -8 = 0
x = -5 or x = 8
4. (x - 6) = 0 or (3x + 7) = 0
x = 6 or x = -7/ 3
5. 5x + 2 = 0 or 2x + 1 = 0
x = -2/ 5 or x = -1/ 2
How to determine the values1. (x+4)(x+7)=0
We have that;
Zero product property;
x + 4 = 0 or x + 7 = 0
x = -4 or x = -7
2. (3x-7)(2x+5)=0
We have that;
Zero product property ;
3x - 7 = 0 or 2x + 5 = 0
x = 7/ 3 or x = -5/ 2
3. x² -3x - 40=0
x² -8x + 5x - 40 = 0
factorize the common multipliers
x(x - 8) + 5(x - 8) = 0
Zero product property;
x + 5 = 0 or x -8 = 0
x = -5 or x = 8
4. 3x² - 11x - 42=0
3x² +7x - 18x - 42 = 0
Factorize further
x(3x + 7) - 6(3x + 7) = 0
Zero product property;
(x - 6) = 0 or (3x + 7) = 0
x = 6 or x = -7/ 3
5. 10x² + 9x + 2 = 0
10x² + 5x + 4x + 2 = 0
Factorize
5x( 2x + 1) + 2 (2x + 1) = 0
Zero product property;
5x + 2 = 0 or 2x + 1 = 0
x = -2/ 5 or x = -1/ 2
Thus, the zero product property states that the product of two non-zero elements is not zero
Learn more about zero product property here:
https://brainly.com/question/1626209
#SPJ1
A parabola is the set of all points in a plane that are equidistant from both a point called the focus and a line called the:_________
Answers
A parabola is the set of all points in a plane that are equidistant from both a point called the focus and a line called the: directrix
A parabola is a plane curve formed by a point moving so that its distance from a fixed point is equal to its distance from a fixed line.
A parabola is approximately U-shaped.
It is the graph of a quadratic function.
A fix point is called as the focus and a fixed straight line is the directrix of the parabola.
The fixed point does not lie on the fixed line. (i.e., the focus does not lie on the directrix of the parabola).
Therefore, A parabola is the set of all points in a plane that are equidistant from both a point called the focus and a line called the: directrix
Learn more about the parabola here:
https://brainly.com/question/771371
#SPJ4
Consider the following rational expression: 4y + 16 y+ 4 Step 2 of 2: Find the restricted values of y, if any, for the given rational expression Answer How to enter your answer (opens in new window) 2
Answers
The given rational expression is 4y + 16 y + 4. To find the restricted values of y, we need to identify any values of y that would make the expression undefined.
In this case, the expression is in the form of a sum, so we don't have any denominators that could lead to division by zero. Therefore, there are no restricted values of y for this rational expression.
The expression 4y + 16 y + 4 is defined for all real numbers. We can evaluate it for any value of y without encountering any restrictions.
Learn more about rational expression here: brainly.com/question/25292194
#SPJ11