what is the gradient of the straight line AB in the figure above
Answers
can you insert a picture of the figure ?
Related Questions
Given sinz = -4/5 for pi < z < (3pi)/2, find the value of cosz.

Answers
The angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
Given sinz = -4/5 for pi < z < (3pi)/2, we need to find the value of cosz. We can use the trigonometric identity of Pythagorean theorem to find the value of cosz.
According to Pythagorean theorem, sin2θ + cos2θ = 1, where θ is the angle in the right-angled triangle and sin, cos are the trigonometric ratios.
The negative sign for the given sinz indicates that the angle z is in the third quadrant. So, we can take the help of the unit circle to find the value of cosz as shown below:
Here, we have used the Pythagorean identity of sin2z + cos2z = 1 on the unit circle to find the value of cosz. Since the value of sinz is already given, we can find the value of sin2z as: sin2z = sinz x sinz = (-4/5) x (-4/5) = 16/25
Then, we can substitute the value of sin2z in the Pythagorean identity as: cos2z = 1 - sin2z = 1 - (16/25) = 9/25We need to find the value of cosz.
So, we can take the square root of cos2z as: cosz = ±(√(9/25)) = ±(3/5)The sign of cosz can be determined by considering the quadrant of the angle z.
Since the angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
For more questions on angle.
https://brainly.com/question/31615777
#SPJ8
answer please ???!!!! worth a lot of points!!

Answers
Answer:
y = -24x + 8 is changing more quickly
Step-by-step explanation:
the slope of a line illustrates the rate of change
since slope is determined by the coefficient of the 'x' term, we can easily identify it when the equation is in slope-intercept form
the greater the absolute value of the coefficient of the slope is, the steeper the line, or the more rapid the rate of change is
Find the equation of the line that is parallel to the line - 4x– 9y = – 7 and that passes through the
point (-9, – 4).
Answers
Answer:
which revision corrects the inappropriate shift in verb mod? could be,might encounter, use ,would be
Find log1/4 rounded to the nearest hundredth.
Answers
Answer:
-log_4
Step-by-step explanation:
The value of log1/4 rounded to the nearest hundredth is -0.60
Given the parameter which is needed for our Calculation:
log1/4Using a calculator, the value of log1/4 is -0.602059
Rounding to the nearest hundredth, is two digits after the decimal point.
Hence, we have ;
-0.60 (since the value after 0 is less than 5)Therefore, log1/4 is -0.60
Learn more on logarithm :https://brainly.com/question/30226560
#SPJ2
Need help please it’s due today show work

Answers
Answer:
c) +20
Step-by-step explanation:
10 colder goes down
so 30-10= 20
A rental company charges $15 plus $4 per hour to rent a bicycle. If Margie does not want to spend more than $27 for her rental, write and solve an inequality to find how many hours she can rent the bicycle and not spend more than $27. Interpret the solution. Show your Work.
Answers
The total cost for X hours is the fixed cost of $15 plus the variable cost of $4 per hour which is equal to 4*X, so the total cost is 4*X + 15
If Margie does not want to spend more than $27 then the inequality is
4*X + 15 <= 27
4*X <= 12
X <= 3
If Margie does not want to spend more than $27 then she cannot rent the bicycle for more than 3 hours
Answer:
3 hoursStep-by-step explanation:
to understand thisyou need to know about:inequalityinequality word problemssolving word problemslet's create the inequality:let's every hour be x
first condition
A rental company charges $15therefore,
15
plus $4 per hour to rent a bicycle.therefore
15+4x (as per our is x)
last condition
Margie does not want to spend more than $27 for her rental,therefore,
15+4x≤27 (≤ is because as it says"does not want to spend more than $27"
let's solve:few things about solving inequality
the direction of the inequality won't change
if
Add (or subtract) a number from both sidesMultiply (or divide) both sides by a positive numberSimplify a sidethe direction of inequality will change
if
Multiply (or divide) both sides by a negative numberSwapping left and right hand sides\(step - 1 \colon \: define\)
\(15 + 4x \leqslant 27\)
\(step - 2 \colon \: \\ subtract \:15 \: from \: both \: sides\)
\(15 - 15 + 4x \leqslant 27 - 15\)
\(4x \leqslant 12\)
\(step - 3 \colon \: \\ divide \: both \: sides \: by \: 4\)
\( \frac{4x}{4} \leqslant \frac{12}{4} \)
\(x \leqslant 3\)
\( \therefore \: she \: can \: rent \: the \: bicycle \: for \: 3 \: hours\)
Hold on hold on hold on hold on hold on oh my God if seven is an element in the domain of F parentheses X parentheses equals 6X -19 over five what is the corresponding element in the range
Answers
The corresponding element in the range of the function F when 7 is in the domain is 4.6.
The expression for the given function F following as:
F(x) = 6(x) - 19 / 5
The corresponding element in the range of the function F is the output of the function when 7 is input into the function.
To find this output, we can substitute 7 for X in the expression for the function F:
F(7) = 6(7) - 19 / 5
F(7) = 42 - 19 / 5
F(7) = 23 / 5
F(7) = 4.6
Thus, when 7 is in the domain, the equivalent element in the range of the function F is 4.6.
Learn more about the domain and the range here:
brainly.com/question/21027387
#SPJ1
Algebra Question
Let v = (-7,6,-6) and w = (-5,-3,-6) be vectors in R^3. Find the orthogonal projection of v onto w.
Answer:
Projection on w: (-54/14, -159/70, -159/35)
I have the correct answer but I don't know how they got it.
Answers
The orthogonal projection of vector v onto vector w in R^3 is (-54/14, -159/70, -159/35).
To find the orthogonal projection of v onto w, we need to calculate the scalar projection of v onto w and multiply it by the unit vector of w. The scalar projection of v onto w is given by the formula:
proj_w(v) = (v⋅w) / (w⋅w) * w
where ⋅ denotes the dot product.
Calculating the dot product of v and w:
v⋅w = (-7)(-5) + (6)(-3) + (-6)(-6) = 35 + (-18) + 36 = 53
Calculating the dot product of w with itself:
w⋅w = (-5)(-5) + (-3)(-3) + (-6)(-6) = 25 + 9 + 36 = 70
Now, substituting these values into the formula, we have:
proj_w(v) = (53/70) * (-5,-3,-6) = (-54/14, -159/70, -159/35)
Therefore, the orthogonal projection of v onto w is (-54/14, -159/70, -159/35).
In simpler terms, the orthogonal projection of v onto w can be thought of as the vector that represents the shadow of v when it is cast onto the line defined by w. It is calculated by finding the component of v that aligns with w and multiplying it by the direction of w. The resulting vector (-54/14, -159/70, -159/35) lies on the line defined by w and represents the closest point to v along that line.
for such more questions on vector
https://brainly.com/question/15519257
#SPJ8
StartFraction 32 Over 8 EndFraction = StartFraction 28 Over x EndFraction
a.
x = 4
c.
x = 8
b.
x = 28
d.
x = 7
Answers
Answer:
d. x = 7
Step-by-step explanation:
\(\frac{32}{8} = \frac{28}{x}\)
Cross multiply, the denominator "8" is multiplied by numerator "28", while the numerator "32" is multiplied by denominator "x":
8 * 28 = 224
32 * x = 32x
\(32x = 224\)
Divide both sides by 32:
\(\frac{32}{32} = \frac{224}{32}\)
[x = 7]
Can you help me plzz i need it quick

Answers
Answer:
okbhyuugggfububububhhhukjgyi
If 2 = 5, what is 2 3 − 4?
Answers
Answer:
27.5
Step-by-step explanation:
3 = 7.5
4 = 10
5*7.5=37.5-10=27.5
Seriously. 2=5 contradicts.
(5)3-4
5(3)=15
15-4=11
Given ω=\(\frac{3-2i}{5-6i}\) , find ω in the a+bi form.
Answers
Answer:
Solution is given in the photo
![Given =[tex]\frac{3-2i}{5-6i}[/tex] , find in the a+bi form.](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/nu38BWTTR6e0HTPj1Es9UzQ51eYzOJHv.jpeg)
Rewrite the following polynomial in standard form. 2 - 9x⁴ - 1/4×
Answers
Answer:
-9x^4-1/4x+2
Step-by-step explanation:
To write any polynomial in standard form, we look at the degree of each term. Then, we order each term by degree, from largest to smallest, from left to right.
2 - 9x⁴ - 1/4×
-9x^4-1/4x+2
In the proportion 12/36 = 2/6 the terms are called the means are

Answers
Given the proportion:
\(\frac{12}{36}=\frac{2}{6}\)Let's determine the terms that are called the means.
In a proportion, the second and third terms are called the means, while the first and last terms are called the extremes.
Let's take the proportion below as an example:
\(\begin{gathered} \frac{a}{b}=\frac{c}{d} \\ \\ a\colon b=c\colon d \end{gathered}\)The means are b and c, while the extremes are a and d.
The given proportion can be written as:
\(12\colon36=2\colon6\)Here, the second and third terms are 36 and 2 . Therefore, we can say the means of the proportion are 36 and 2.
ANSWER:
36 and 2
The function f(x) is graphed. It represents a translation of the square root function g(x) = . What equation represents the graph of f(x)? f(x) = f(x) = f(x) = – 1 f(x) = + 1
Answers
Using translation concepts, the equation of the graph of f(x) is given as follows:
\(f(x) = \sqrt{x - 1}\)
What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
Function f(x) is a shift right of one unit of the square root function, hence x -> x - 1 and the equation is given by:
\(f(x) = \sqrt{x - 1}\)
More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
which of the following equations is non-linear?

Answers
Answer:
the last one
Step-by-step explanation:
it is because there are y² which shows that the it is quadratic equation, not a linear equation
Answer:
last
Step-by-step explanation:
linear are all the equation that have variable x and y to the first degree
the last one as a y^2 so in not linear
#3 Preimage point B is
located at (5,-4).
B' is located at (20, -16).
Write the algebraic rule for
the transformation.
Answers
The algebraic rule for the transformation is B' = (Bx + 15, By - 12)
Given data ,
To determine the algebraic rule for the transformation from point B to point B', we need to find the equations that relate the coordinates of the preimage point B to the image point B'.
Let's denote the translation amounts in the x-direction and y-direction as (dx, dy). The coordinates of B' can be obtained by adding these translation amounts to the coordinates of B:
B' = (Bx + dx, By + dy)
Given that B is located at (5, -4) and B' is located at (20, -16), we can calculate the translation amounts:
dx = 20 - 5 = 15
dy = -16 - (-4) = -12
Hence , the algebraic rule for the transformation is B' = (Bx + 15, By - 12)
To learn more about translations click :
https://brainly.com/question/19007400
#SPJ1
How do I solve this system of linear equations

Answers
The solution for the system of linear equations is: x₁ = -1, x₂ = -3, x₃ = 3 and x₄ = -2
How do you solve for the system of linear equations?To solve this system of linear equations, we can use the Gaussian elimination method. First, let's represent the system as an augmented matrix:
| 1 0 2 0 | 5 |
| 0 1 0 -1 | -1 |
| -1 -1 1 0 | 1 |
| 0 0 2 -1 | 4 |
Add the first row to the third row to eliminate x₁ in the third row:
| 1 0 2 0 | 5 |
| 0 1 0 -1 | -1 |
| 0 -1 3 0 | 6 |
| 0 0 2 -1 | 4 |
Add the second row to the third row to eliminate x₂ in the third row:
| 1 0 2 0 | 5 |
| 0 1 0 -1 | -1 |
| 0 0 3 -1 | 5 |
| 0 0 2 -1 | 4 |
Divide the third row by 3
| 1 0 2 0 | 5 |
| 0 1 0 -1 | -1 |
| 0 0 1 -1/3 | 5/3 |
| 0 0 2 -1 | 4 |
Subtract twice the third row from the fourth row to eliminate x₃ in the fourth row
| 1 0 2 0 | 5 |
| 0 1 0 -1 | -1 |
| 0 0 1 -1/3 | 5/3 |
| 0 0 0 -1/3 | 2/3 |
Multiply the fourth row by -3 to get x₄
| 1 0 2 0 | 5 |
| 0 1 0 -1 | -1 |
| 0 0 1 -1/3 | 5/3 |
| 0 0 0 1 | -2 |
We can use back substitution to find the values of x₁, x₂, and x₃:
x₄ = -2
x₂ - x₄ = -1 which is x₂ = -1 + (-2) = -3
x₃ - (1/3)x₄ = 5/3 therefore; x₃ = 5/3 + (1/3)(-2) = 3
x₁ + 2x₃ = 5 therefore; x₁ = 5 - 2(3) = -1
The above answer is in response to the full question below;
Solve this system of linear equations
x₁ + 2x₃ = 5
x₂ - x₄ = -1
-x₁ - x₂ + x₃ = 1
2x₃ - x₄ = 4
Find more exercises on linear equations;
https://brainly.com/question/29739212
#SPJ1
Lucy received 5/6 of the 180 votes cast for class secretary. How many votes did she receive?
Answers
Answer:
150 votes
Step-by-step explanation:
If Lucy got 5/6, we can do the following.
(5/6) * 180 = 150
So, Lucy got 150 votes.
Answer:
150
Step-by-step explanation:
We can first divide 180 by 6:
180/6 = 30
Then multiply that by 5:
5 × 30 = 150
Simplify (7ty)(3t)
(answer fast please)
Answers
Answer:
I think they are correct
Desperate Need Of Help

Answers
The domain and range of the graph above in interval notation include the following:
Domain = [-6, 3]
Range = [-3, 3]
What is a domain?In Mathematics and Geometry, a domain refers to the set of all real numbers (x-values) for which a particular function (equation) is defined.
In Mathematics and Geometry, the horizontal portion of any graph is used to represent all domain values and they are both read and written from smaller to larger numerical values, which simply means from the left of any graph to the right.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = [-6, 3] or -6 ≤ x < 3.
Range = [-3, 3] or -3 < y < 3
Read more on domain here: brainly.com/question/9765637
#SPJ1
xA radioactive isotope is decaying at a rate of 20% every hour. Currently there are 15 grams of the substance.
Questions:
A. Write an equation that will represent the number of grams present after n hours
B. How much will be left after 24 hours (one day)? (Round to the nearest hundredth)
C. After how many hours will there be approximately one gram left?
Answers
B. After 24 hours, approximately 2.49 grams will be left.
C. After approximately 18.13 hours, there will be approximately one gram left.
A. To represent the number of grams present after n hours, we can use the equation:
N(n) = 15 × (1 - 0.2)^n
Where:
N(n) is the number of grams present after n hours,
15 is the initial amount of the substance in grams,
0.2 represents the decay rate of 20% per hour, and
^n represents the exponentiation operation.
B. To find out how much will be left after 24 hours, we can substitute n = 24 into the equation from part A:
N(24) = 15 × (1 - 0.2)^24
Calculating this expression, we find that approximately 2.49 grams will be left after 24 hours.
C. We need to determine the number of hours it takes until there is approximately one gram left. We can set up the equation:
1 = 15 × (1 - 0.2)^n
To solve for n, we can divide both sides of the equation by 15 and then take the logarithm (base 0.8) of both sides:
log(0.8)(1/15) = n
Using a calculator or logarithmic properties, we find that approximately 18.13 hours are required until there is approximately one gram left.
Therefore, the answers are:
B. After 24 hours, approximately 2.49 grams will be left.
C. After approximately 18.13 hours, there will be approximately one gram left.
for such more question on grams
https://brainly.com/question/13439286
#SPJ8
15.78=5.28+6x
I just need help with this math problem
Answers
Answer: x=1.75
Step-by-step explanation:
pls answer will give brainliest answer

Answers
Answer:
∠A= ∠E, ∠H = ∠D
and the last one
Step-by-step explanation:
opposite angles are equal, alternative interior angle are equal.
Answer:
∠A = ∠E and ∠H = ∠D.
∠E = ∠H and ∠F = ∠G
Step-by-step explanation:
Angles A and E are one set of corresponding angles and angles H and D are another set. Corresponding angles are always congruent to each other and thus equal. Therefore, ∠A = ∠E and ∠H = ∠D.
Angles E and H are one set of vertical angles and angles F and G are another set. Vertical angles are also always congruent to each other and thus equal. Therefore ∠E = ∠H and ∠F = ∠G
Help please I will give brainlest

Answers
Which set of numbers can represent the side lengths, in centimeters, of a right triangle?
Answers
A set of numbers that can represent the side lengths, in centimeters, of a right triangle is any set that satisfies the Pythagorean theorem, where the square of the hypotenuse's length is equal to the sum of the squares of the other two sides.
A right triangle is a type of triangle that contains a 90-degree angle. According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Let's consider a set of numbers that could represent the side lengths of a right triangle in centimeters.
One possible set could be 3 cm, 4 cm, and 5 cm.
To verify if this set forms a right triangle, we can apply the Pythagorean theorem.
Squaring the length of the shortest side, 3 cm, gives us 9. Squaring the length of the other side, 4 cm, gives us 16.
Adding these two values together gives us 25.
Finally, squaring the length of the hypotenuse, 5 cm, also gives us 25. Since both values are equal, this set of side lengths satisfies the Pythagorean theorem, and hence forms a right triangle.
It's worth mentioning that the set of side lengths forming a right triangle is not limited to just 3 cm, 4 cm, and 5 cm.
There are infinitely many such sets that can be generated by using different combinations of positive integers that satisfy the Pythagorean theorem.
These sets are known as Pythagorean triples.
Some other examples include 5 cm, 12 cm, and 13 cm, or 8 cm, 15 cm, and 17 cm.
In summary, a right triangle can have various sets of side lengths in centimeters, as long as they satisfy the Pythagorean theorem, where the square of the hypotenuse's length is equal to the sum of the squares of the other two sides.
For similar question on hypotenuse's.
https://brainly.com/question/30390037
#SPJ8
Find the volume of the figure shown below.
A)42 1/2 units^3
B)11 1/4 units^3
C)14 1/4 units^3
D)80 1/4 units^3
E)None of these answers are correct
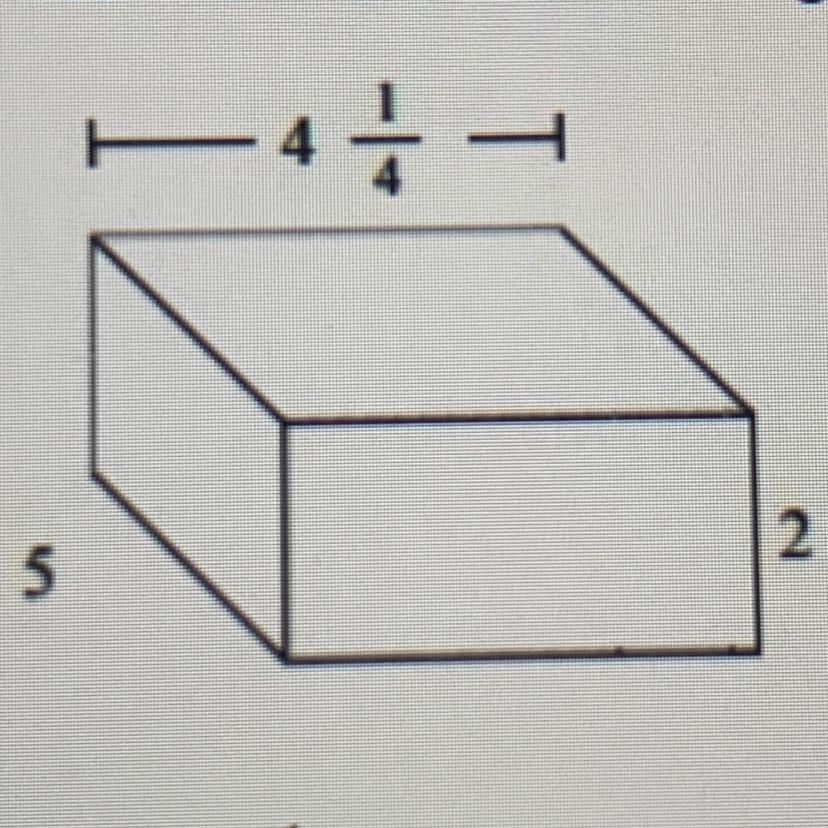
Answers
Answer:
A. 42½ units
Step-by-step explanation:
the volume = 5×2×4¼ = 10×4¼ = 42½
A student borrows 4000 at 15% for 3 months to pay tuition find the total amount due using simple interest
Answers
Answer:
Step-by-step explanation:
\(A=p(1+rt)\\p=4000\\r=15 \%\\t=\frac{1}{3}years\\\)
∴ \(A=4000[1+(0.15\times\frac{1}{3})]\\A=4,000*0.05\\A= 4,200 (200\\)
Answer:
4,150
Step-by-step explanation:
Whenever Deven and Laura owe each other money, they "pay" each other using stickers. They've agreed that a Harry Potter sticker is worth 49 dollars and a Twilight sticker is worth 35 dollars. They can even use stickers as "change" if one person overpays the other. For example, if Deven owes Laura 189 dollars, he can give her 6 Harry Potter stickers ($6 \cdot 49 = 294$ dollars), and she can return 3 Twilight stickers ($3 \cdot 35 = 105$ dollars). This trade is like a transfer of $294-105=189$ dollars. What is the smallest positive debt, in dollars, that can be paid off using sticker trading?
Answers
The smallest positive debt that can be paid off using sticker trading is $7$ dollars.
To find the smallest positive debt that can be paid off using sticker trading, we need to consider the values of the stickers (in dollars) and find the smallest positive amount that can be reached through a combination of these values.
Given that a Harry Potter sticker is worth $49 and a Twilight sticker is worth $35, we can approach this problem using the concept of the greatest common divisor (GCD) of these two values.
The GCD of $49$ and $35$ is $7$. This means that any multiple of the GCD can be represented using these sticker values.
In other words, any positive multiple of $7$ dollars can be paid off using sticker trading.
Therefore, the smallest positive debt that can be paid off using sticker trading is $7$ dollars.
For such more questions on debt
https://brainly.com/question/28929846
#SPJ8
find the missing value

Answers
Answer: P=$7,1333.33
Step-by-step explanation:
Equation: P=A/(1+rt)