what is the estimated mean systolic blood pressure for the population of low birth weight infants whose gestational age is 31 weeks?
Answers
The estimated mean systolic blood pressure for the population of low birth weight infants whose gestational age is 31 weeks is unknown. In order to obtain an estimated mean systolic blood pressure for a population, it is necessary to collect data on that population and perform statistical analysis.
Data can be collected by sampling from the population of low birth weight infants whose gestational age is 31 weeks. The sample should be randomly chosen in order to minimize bias, and it should be representative of population. The data can be analyzed using statistical software or by hand using formulas. The estimated mean systolic blood pressure can be calculated by taking the sum of the systolic blood pressures and dividing by the sample size. without data, it is impossible to provide an estimated mean systolic blood pressure for the population of low birth weight infants whose gestational age is 31 weeks. A sample must be randomly selected from the population, and statistical analysis must be performed on the data to determine the estimated mean.
To know more about mean visit:-
https://brainly.com/question/30094057
#SPJ11
Related Questions
Suppose you have a job that pays $13.50 per hour and you work anywhere from 10 to 40 hours per week. a. Write an equation, with a restriction on the variable I, that gives the amount of money, y, you will earn for working 2 hours in one week. y = _____ , Preview with ____ <= x <= ____ b. Use the function rule you have written in part a. to find the y values for the given z values: x = 10, y = ___ x = 20, y= ___
x = 30, y = ____. x = 40, y = ____ c. Construct a line graph from the information found in b. 520+ -480+ 440+ 400- 360 320- 280- 240 200 160+ 120+ 80- 40+ 10 20 30 40 Clear All Draw: Line Dot Open Dot d. State the domain and range of this function. Domain: ____ <= x <= ______
Range: <= y <= _____
e. What is the minimum amount you can earn in a week with this job? You'll earn at least $ ______.
What is the maximum amount? You can earn up to $ ____.
Answers
The maximum amount you can earn is $540
a. y = 13.50x , 10 <= x <= 40
b. x = 10, y = 135; x = 20, y= 270; x = 30, y = 405; x = 40, y = 540
c. Domain: 10 <= x <= 40; Range: 0 <= y <= 540
d. The minimum amount you can earn in a week with this job is $135. The maximum amount you can earn is $540.
To learn about Domain
brainly.com/question/29452843
#SPJ11
suppose that the population of all north american domesticated cats have a mean weight of 12 pounds and standard deviation of 2.5 pounds. the frequency distribution of north american domesticated cat weights is approximately normal. about 95% of the mean weights from samples of size 100 cats from this population fall between what two values (note: assume the sampling distribution of sample means is approximately normal)?
Answers
Answer. The correct option is (E). 9.5 and 14.5
Explanation for step 1This is because 95% of the mean weights from samples of size 100 cats from this population will fall between 9.5 and 14.5 pounds. The other answers are incorrect because they do not fall within the range of 95% of the mean weights from samples of size 100 cats from this population
About 95% of the mean weights from samples of size 100 cats from this population would fall between approximately 11.51 pounds and 12.49 pounds.
To determine the range within which 95% of the mean weights from samples of size 100 cats would fall, we can use the concept of the confidence interval.
Given:
Population mean weight (μ) = 12 pounds
Population standard deviation (σ) = 2.5 pounds
Sample size (n) = 100 cats
Since the population distribution is assumed to be approximately normal, the sampling distribution of sample means will also be approximately normal. To calculate the range, we can use the formula for the confidence interval:
Confidence Interval = sample mean ± (z * standard error)
The standard error can be calculated using the formula:
Standard Error = σ / √n
Using a 95% confidence level, the corresponding z-value is approximately 1.96 (obtained from standard normal distribution table).
Plugging in the values:
Standard Error = 2.5 / √100 = 0.25
Confidence Interval = 12 ± (1.96 * 0.25)
Calculating the values:
Lower limit = 12 - (1.96 * 0.25) ≈ 11.51 pounds
Upper limit = 12 + (1.96 * 0.25) ≈ 12.49 pounds
Know more about mean weights here:
https://brainly.com/question/16170417
#SPJ11
Given x1 = x2 – x1(x1^2 + x2^2 -1) and x2 = -x1 - x2(x1^2 + x2^2 -1) as state dr do equations. Polar coordinates are r and tetha. Please prove that dr/dt = -r(r^2 -1) and dtetha/dt= -1. Then explain why r=1 is a stable limit cycle.
Answers
To solve this problem, we'll start by finding the polar coordinates r and θ in terms of x1 and x2. We have r^2 = x1^2 + x2^2, tan(θ) = x2/x1.
Taking the derivative of x1 with respect to time t, we have: dx1/dt = dx2/dt - 2x1(dx1^2 + x2^2 - 1) - x1^2(2x1dx1 + 2x2dx2)
Similarly, the derivative of x2 with respect to t is: dx2/dt = -dx1/dt -2x2(dx1^2 +x2^2 -1) - x2^2(2x1dx1 + 2x2dx2) Using the chain rule, we can write: dr/dt = (x1dx1 + x2dx2)/r dθ/dt = (1/r^2)(x2dx1 - x1dx2)
Substituting dx1/dt and dx2/dt in these equations and simplifying, we get: dr/dt = -r(r^2 -1) dθ/dt = -1 Now, to prove that r=1 is a stable limit cycle, we can use the method of linearization.
This involves finding the Jacobian matrix at the equilibrium point r=1, θ=0: Jacobian = [[-3 -1], [-1 -3]] Taking the eigenvalues of this matrix, we get -4 and -2.
Since both eigenvalues are negative, we conclude that the equilibrium point corresponds to a stable limit cycle at r=1, θ=0. In summary, we have shown that the differential equations for dr/dt and dθ/dt are -r(r^2 -1) and -1, respectively. We have also demonstrated that r=1 is a stable limit cycle.
For more questions like Polar coordinates visit the link below :
https://brainly.com/question/14955163
#SPJ11
Your uncle is trying to decide between the purchase of a sports car or a SUV. The
sports car is cheaper to buy but costs more to insure. Specifically, the sports car
would cost $5000 plus $2500 each year for insurance, while the SUV would be
$8000 plus $800 per year to insure. After how many years would the amount
spent on each vehicle be the same?
Answers
The number of years it will take such that amount spent on each vehicle is the same will be 2.
How to form an equation?Determine the known quantities and designate the unknown quantity as a variable while trying to set up or construct a linear equation to fit a real-world application.
In other words, an equation is a set of variables that are constrained through a situation or case.
Suppose after x years the amount will be the same.
5000 + 2500x = 8000 + 800x
2500x - 800x = 8000 - 5000
1700x = 3000
x = 1.76
Since x must be a whole number so it will round up so x = 2.
Hence "The number of years it will take such that amount spent on each vehicle is the same will be 2".
For more about the equation,
https://brainly.com/question/10413253
#SPJ1
2p + 5q = 48
yng true answer po
thank you:)
Answers
Answer: p = 24 − 5 q /2
Step-by-step explanation:
Answer:
\(p = \frac{ - 5}{2} q + 24\)
Step-by-step explanation:
Let's solve for p:
\(2p+5q=48\)
Step 1: Add -5q to both sides.
\(2p+5q+−5q=48+−5q\)
\(2p=−5q+48\)
Step 2: Divide both sides by 2.
\( \frac{2p}{2} = \frac{ - 5q + 48}{2} \)
\(p= \frac{ - 5}{2} q+24\)
4. (2 pts) A roll of 32 bills contains only $5 bills and $10 bills. If the value of the roll is $220,then how many of each bill are in the roll?

Answers
Given:
Total number of bills is, N = 32.
Total cost of the bill is, C = $220.
The first type of bill contans $5 bills and second type of bill contains $10 bills in the roll.
Explanation:
Consider the numer of $5 bills as x and $10 bills as y.
Then, the equation for total number of bill can be written as,
\(\begin{gathered} x+y=N \\ x+y=32 \\ x=32-y\text{. . . . . . . (1)} \end{gathered}\)Similarly the total cost of the bill can be written as,
\(undefined\)The fox population in a certain region has a continuous growth rate of 6 percent per year. It is estimated that the population in the year 2000 was 22300. (a) Find a function that models the population t years after 2000 (t = 0 for 2000). Hint: Use an exponential function with base e. Your answer is P(t) = Preview (b) Use the function from part (a) to estimate the fox population in the year 2008. Your answer is (the answer must be an integer) Preview
Answers
The function that models the population t years after 2000 is22300 × e^(0.06t), The estimated fox population in the year 2008 is 36081. This can be answered by the concept of exponential function.
The question asks to find a function that models the population of foxes in a certain region with a continuous growth rate of 6 percent per year starting from the year 2000. It also asks to estimate the fox population in the year 2008 using this function.
a. Let P(t) be the population of foxes t years after 2000. Since the growth rate is continuous, we can use an exponential function with base e to model the population. We know that P(0) = 22300 (the population in the year 2000), and the annual growth rate is 6%. Therefore, we can write:
P(t) = 22300 × e^(0.06t)
b. To estimate the fox population in the year 2008, we need to find P(8) since t = 8 represents 8 years after 2000. Substituting t = 8 into the equation above, we get:
P(8) = 22300 × e^(0.06×8) = 22300 × e^0.48 ≈ 36081
Therefore, the estimated fox population in the year 2008 is 36081.
To learn more about exponential function here:
brainly.com/question/11487261#
#SPJ11
a) Complete the table of values for
y = 2x² + x
X -2 -1
y
1
0 1
3
2

Answers
Here's the completed table of values for y = 2x^2 + x
7,1,9
How to calculate the values of X and Y?To find the value of y for each x, substitute x into the equation and simplify:
For \(x = -2: y = 2(-2)^2 + (-2) = 7\)
For\(x = -2: y = 2(-2)^2 + (-2) = 7\)
For\(x = 0: y = 2(0)^2 + 0 = 1\)
For \(x = 1: y = 2(1)^2 + 1 = 4\)
For\(x = 2: y = 2(2)^2 + 2 = 9\)
To know more about tables visit:-
https://brainly.com/question/30244091
#SPJ1
2x + 5 - 3 +8x combine like terms
Answers
Answer:
10x+2
Step-by-step explanation:
Hope you have a good day, Loves!~
If it takes 2/3 hours to paint 2/5 room how many hours does it take to paint one room
Answers
Step-by-step explanation:
2/3 hours for 2/5 room.
that means
5×2/3 = 10/3 hours for 5×2/5 = 2 rooms
and then 1 room in 10/3 / 2 = 5/3 hours
3. 7.NS.1.2
Evaluate the following expression.
2 + (3 – 2 x 2) x 1

Answers
Answer:
Step-by-step explanation:
2 + (3 – 2 x 2) x 1
This is what I remember, but you need to check this order of arithmetic operations.
Parentheses first then exponents ( you don't have any) multiplication and division left to right and then addition and subtraction again left to right
2 + (3 – 2 x 2) x 1 so 3 – 2 x 2 equals 3 - 4 which equaltes to
2 + (-1) x 1 -1 x 1 = -1
2 + (-1) x 1 is to clearer to me than 2 + -1 x 1 maybe not
2 + -1
1 it confusing but use your calculator to practice
Evaluate 4(3x+6) when x = 15
Answers
Answer:
204
Step-by-step explanation:
4(3x+6)
Substitute the x with 15
4(3*15+6)
4( 45 + 6)
Distributive property
4*45 + 4*6
180 + 24
204
Hey there!
The answer to your question is \(204\)
To evaluate this, we simply start by plugging the given x value, 15, into the expression, and then solve:
\(4[3(15) + 6]\) Plug in X
\(4(45 + 6)\) Multiply
\(180 + 24\) Distribute the 4
\(204\) Add
Hope it helps and have a great day!
Consider the following. cos(x) + vy = 6 (a) Find y' by implicit differentiation. (b) Solve the equation explicitly for
y and differentiate to get y' in terms of x. y' (c) Check that your solutions to parts (a) and (b) are consistent by
substituting the expression for y into your solution for part (a). y'
Answers
(a) The derivative of y with respect to x, y', is given by -sin(x) + v(dy/dx) + y(dv/dx) = 0. (b) Solving the equation for y and differentiating gives y' = [(cos(x))(dv/dx)]/v^2. (c) Substituting the expression for y into the solution from part (a) confirms the consistency of the solutions.
To find the derivative of y with respect to x, we can use implicit differentiation. Let's go through the steps:
(a) To find y', we differentiate both sides of the equation cos(x) + vy = 6 with respect to x.
Differentiating cos(x) with respect to x gives us -sin(x).
For the term vy, we need to use the product rule. Let u = v and v = y.
Differentiating u = v with respect to x gives us du/dx = dv/dx.
So, differentiating vy with respect to x gives us v(dy/dx) + y(dv/dx).
Since we are differentiating with respect to x, the term dv/dx is the derivative of v with respect to x.
Now, we can put these results together to find y':
-sin(x) + v(dy/dx) + y(dv/dx) = 0
(b) To solve the equation explicitly for y, we rearrange the equation cos(x) + vy = 6 to isolate y.
Subtracting cos(x) from both sides gives vy = 6 - cos(x).
Dividing both sides by v gives y = (6 - cos(x))/v.
To find y' in terms of x, we need to differentiate y = (6 - cos(x))/v with respect to x.
Using the quotient rule, we have:
y' = [(v(0) - (6 - cos(x))(dv/dx))/(v^2)]
Simplifying, we get:
y' = [(cos(x))(dv/dx)]/v^2
(c) To check the consistency of our solutions, we substitute the expression for y from part (b) into the equation from part (a).
cos(x) + v[(6 - cos(x))/v] = 6
Canceling out v on the right side gives:
cos(x) + (6 - cos(x)) = 6
Simplifying, we have:
cos(x) - cos(x) + 6 = 6
0 + 6 = 6
This is a true statement, confirming the consistency of our solutions.
So, the final expression for y' is [(cos(x))(dv/dx)]/v^2.
Learn more about equation here:
https://brainly.com/question/29174899
#SPJ11
Which type of parent function does the equation f(x)=1/x represents
Answers
Answer:
Parent functions are the base function of a family function. is the parent function of the square root function
Step-by-step explanation:
Given that:
f(x)={x}
The parent function of cube root function is:
f(x)=x^3
The parent function of reciprocal function is:
f(x)=1/x
The parent function of an absolute function is:
f(x)=|x|
The parent function of square root function is:
f(x)=x
By comparing the above parent function to f(x)=x, we can conclude that f(x)=x is the parent function of square root function.
(So your answer is Square root)
jessica made $234 for 13 hours of work. At the same rate, how many hours would she have to work to make $162?
Answers
Answer: 9 hours
We would get:
1 hour of work = $18
162 divided by 18 = 9
So she would have to work 9 hours
Answer:
9 hours
Step-by-step explanation:
Step One: A rate is the same thing as ratio. This just means that there is a proportion. For example, for every 3 dogs, there are 4 cats. This would mean that for 6 dogs there are 8 cats, and so on.
Step Two: Okay, because these numbers are larger, it is easiest to scale it back to one. The proportion or rate given is $234/13 hours. We would divide by 13 to get it to 1: $18/1 hour. The proportion is usually a decimal, but these numbers happen to divide nicely.
Step Three: Now, we can do 162/18 to see what the scale is, or how much times larger it is: 162/18=9.
Step Four: Lastly, just do 1 times 9, which tells it is 9 hours. To check the work, make sure 9 is less than the original proportion; it should take less time to make less money. 9 is less than 13, so this is the answer!
Write an equation of a parabola that opens down, has been vertically compress and has been shifted down 6 and right 2.
Answers
The equation of a parabola that opens downwards, has been compressed vertically and has been shifted down 6 and to the right 2 will be:
y=a(x-h)^2+kWhat does each term in the equation mean?The terms (h,k) correspond to the vertex of the parabola.The letter a is a constant that determines the "slope" of the parabola.The letter x and y are the coordinates of any point on the parabolaIf the parabola was shifted 6 units down and 2 units to the right, the vertex will be at the point (2, -6).To create a vertically compressed parabola that opens downwards, we want the value of a to be negative. To compress the parabola vertically, we want the value of a to be less than 1.
So let's choose a = -1/4. So the equation becomes:
y = (-1/4)(x-2)^2 - 6Therefore, this equation describes a parabola that opens downwards, has been compressed vertically by a factor of 1/4, and has been shifted 6 units down and 2 units to the right.
Find out more parabola on:
https://brainly.com/question/28747870
#SPJ1
Find the missing side length
Round to the nearest tenth
The answer is 4.8
Please show all steps thank u

Answers
Answer:
x ≈ 4.8
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Trigonometry
[Right Triangles Only] SOHCAHTOA[Right Triangles Only] cos∅ = adjacent over hypotenuseStep-by-step explanation:
Step 1: Identify Variables
Angle measure = 58°
Adjacent side of angle = x
Hypotenuse = 9
Step 2: Solve for x
Substitute [cosine]: cos58° = x/9Isolate x: 9cos58° = xEvaluate: 4.76927 = xRewrite: x = 4.76927Round: x ≈ 4.8Answer:
if you have the answer then wha.
Step-by-step explanation:
Mrs. Thomas has two rolls of garden edging that are each 96 inches long.
She wants to make two new flower beds in her back yard. Each flower bed
will be bordered by one roll of the edging. One flower bed will be in the
shape of a quadrilateral. The other will be in the shape of a triangle.
Mrs. Thomas decides to make a scale drawing of each flower bed using a
scale of 1 centimeter = 5 inches. What will be the total length of each roll
of edging in her scale drawings?
Answers
The total length of each roll of edging in Mrs. Thomas's scale drawings will be 19.2 cm.
How to find the total length ?To find the total length of each roll of edging in her scale drawings, we need to convert the length from inches to centimeters using the given scale.
To convert the length to centimeters:
( Length in cm ) / ( Length in inches ) = ( 1 cm ) / ( 5 inches )
x / 96 inches = 1 cm / 5 inches
x 5 inches = 96 inches x 1 cm
5x = 96 cm
x = 96 cm / 5
x = 19.2 cm
Find out more on total length at https://brainly.com/question/3283503
#SPJ1
What is 1978 times 45
Answers
Answer:
89010
Step-by-step explanation:
1978 times 45 will equal 89010 its very simple step wise.
Answer:
89010
Step-by-step explanation:
How do you find number 6 both a and b? Please answer!

Answers
The area of the semicircle and composite circle are 89.97 square feet and 51 π/2 square cm respectively
Area of a circle and semicircleThe formula for calculating the area of circle and semi circle is expressed as:
Area of a circle = πr²
Area of a semicircle = πr²/2
where
r is the radius of a circle
6a) The given shape is a semi circle
A = πr²/2
A = π(11)²/2
A = 121(3.14)/2
A = 189.97 square feet
6b) For the composite circles, the area will be expressed as;
A = π(10)²/2 - π(7)²/2
A = 100π/2 - 49π/2
A = 51 π/2 square cm
Hence the area of the semicircle and composite circle are 89.97 square feet and 51 π/2 square cm respectively
Learn more on circles here: https://brainly.com/question/24375372
#SPJ1
Determine if the following statement is true or false.
When two events are disjoint, they are also independent.
Answers
The statement, When two events are disjoint, they are also independent is false.
In a sample space, we can use probability laws to determine the probabilities of these events and how they relate to each other. Disjoint Events: Two events are non-overlapping or mutually exclusive if they have no common outcome. Mathematically, this can be written as, P(B ∩ A) = 0 --(1)
Independent Events: Events are independent when they do not "affect" the probability of another event occurring. Mathematically written as:
P(B/A) = P(B) P(A and B)
=> P(B ∩ A) = P(B) × P(A) --(2)
(1) ) and (2) events cannot be independent unless they overlap. That is, if events do not overlap, they are also dependent. Hence, disjoint events are not independent that means the above statement is false.
To learn more about Disjoint events, refer :
https://brainly.com/question/14634231
#SPJ4
in a weighted, connected graph with edge weights being not necessarily distinct, if one mst has k edges of a certain weight w, then any other mst must also have exactly k edges of weight w. is this true or false
Answers
This statement is false. In a weighted, connected graph with edge weights not necessarily distinct, if one Minimum Spanning Tree (MST) has k edges of a certain weight w, it is not guaranteed that any other MST must also have exactly k edges of weight w.
1. In a weighted graph, each edge has a weight (or cost) associated with it.
2. A connected graph means there is a path between any pair of vertices.
3. An MST is a subgraph that connects all the vertices in the graph, without any cycles, and with the minimum possible total edge weight.
However, there can be multiple MSTs for a given graph, and their edge weights distribution might not be the same. This is because MSTs are primarily focused on minimizing the total weight, not necessarily preserving the number of edges with a specific weight. Different MSTs may use different sets of edges to achieve the minimum total weight, so they might not have the exact same count of edges with weight w.
Learn more about graph here:
https://brainly.com/question/31741535
#SPJ11
Find the linear approximation of the f(x,y)=x+yx at the point (1,6)
Answers
\(L(x,y)=f(a,b)+f_x'(a,b)(x-a)+f_y'(a,b)(y-b)\\\\f(x,y)=x+yx\\(a,b)=(1,6)\\\\f(1,6)=1+6\cdot1=7\\f'_x(x,y)=1+y\\f'_x(1,6)=1+6=7\\f'_y(x,y)=x\\f'_y(1,6)=1\\\\L(1,6)=7+7\cdot(x-1)+1\cdot(y-6)\\L(1,6)=7+7x-7+y-6\\L(1,6)=7x+y-6\)
The angle between 0∘ and 360∘ that is coterminal with the −252∘ angle is degrees.
Answers
The angle coterminal with -252° between 0° and 360° is 108°.
To find the angle between 0° and 360° that is coterminal with the -252° angle, we can add or subtract multiples of 360° until we get an angle within the desired range.
Since the given angle is negative, we can add 360° to it repeatedly until we get a positive angle:
-252° + 360° = 108°
Therefore, the angle between 0° and 360° that is coterminal with the -252° angle is 108°.
Coterminal angles are angles that have the same initial and terminal sides but may differ in the number of complete revolutions made. In this case, by adding 360° to the given angle, we obtain an angle that falls within the desired range.
Learn more about angle coterminal
brainly.com/question/21384986
#SPJ11
a+c=r+d solve for a, answer please :(
Answers
Answer:
a = r + d - c
Step-by-step explanation:
a + c = r + d
You want a alone on the left side. c is being added to a.
To get rid of the c, you must subtract c from the left side, but the rule of equations is that you must do the same operation to both sides of the equation. We subtract c from both sides of the equation.
a + c - c = r + d - c
c - c = 0, so the c is eliminated from the left side.
We now have
a + 0 = r + d - c
a = r + d - c
Answer:
a = r + d - c
Step-by-step explanation:
All we do is transpose c to the other side to isolate a.
A player in a board game rolls a six-sided
number cube labeled 1 through 6 once.
Determine the theoretical probability of
rolling a 1 or 2.
Answers
Answer:
A six sided number from 1 to 6 is rolled in a game.
Step-by-step explanation:
Theoretical probability of rolling a 1 or 2.
1) The cube has 6 faces so the total number of the outcome would be 6 only.
2) As per the question we need only 1 or 2 so the favorable outcome would be 2.
3) P(E) = favorable outcome/ total number of outcome
P(E) = 2/6
P(E) = 1/3
Theoretical probability of rolling a 1 or 2 is 1/3
which expression is the equivalent to the given expression
(3m-4)³(3m³)
Answers
Answer:
81m^6 - 323 m^5 + 432m^4 - 192m^3
Step-by-step explanation:
Comment
If you are given choices, you should list them please. Otherwise we cannot be certain our answers are taken far enough.
The general formula for expanding a binomial raised to the third power is
(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3
Solution
To modify the general formula to suit this problem, let
a = 3m
b = - 4
When that is done, the general equation becomes
(3m)^3 - 3* (3m)^2 * 4 + 3 * 3m * 4^2 - 4^3
(3m - 4)^3 = 27m^3 - 108 m^2 + 144m - 64
Multiply everything in the 4-nomial by 3m^3
(27m^3 - 108 m^2 + 144m - 64)3m^3
81m^6 - 323 m^5 + 432m^4 - 192m^3 which is your answer. I see why you didn't include it, with other (incorrect) possibilities.
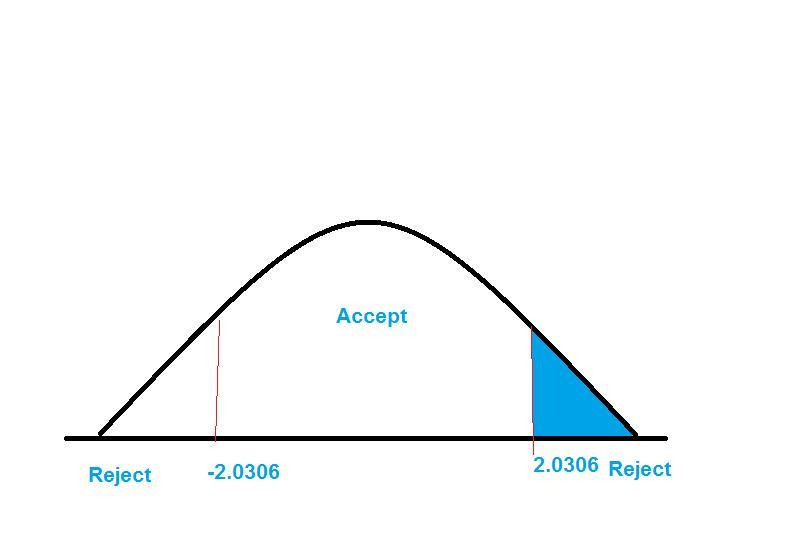
A large software company gives job applicants a test of programming ability, and the mean for that test has been 160 in the past. A random sample of 36 job applicants are selected from a large university, and they produce a sample mean score of 165 with a sample standard deviation of 12. At the 0.05 significance level, test the claim that the mean score for students from this university is greater than 160. State the null and alternative hypotheses symbolically. Which test procedure is appropriate to perform the required hypothesis test? Compute the value of the test statistic. Determine the P-value or provide the rejection region. What is your conclusion about the hypothesis test?
Answers
Answer:
Since the computed value of t= 0.833 does not fall in the critical region we therefore do not reject H0 and may conclude that population mean is greater than 160. Or the sample comes from population with mean of 165.
Step-by-step explanation:
State the null and alternative hypothesis asH0: μ= 160 against the claim Ha :μ ≠160
Sample mean = x`= 165
Sample standard deviation= Sd= 12
2. The test statistic to use is
t= x`-μ/sd/√n
which if H0 is true , has t distribution with n-1 = 36-1= 35 degrees of freedom
3. The critical region is t< t (0.025(35)= 2.0306
t= x`-μ/sd/√n
4. t = (165-160)/[12/√(36)] = 5/[6] = 0.833
5. Since the computed value of t= 0.833 does not fall in the critical region we therefore do not reject H0 and may conclude that population mean is greater than 160. Or the sample comes from population with mean of 165.
Now
6. The p-value is 0 .410326 for t= 0.8333 with 35 degrees of freedom.
If 16x-2=30 what is the value of 8x-4?
Answers
16x - 2 = 30
+ 2 +2
16x = 32 , x=2
Substitute :
8x - 4 = 8(2) - 4 = 16-4 = 12!
Answer:
12
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDASEquality PropertiesStep-by-step explanation:
Step 1: Define 1st equation
16x - 2 = 30
Step 2: Solve for x
Add 2 on both sides: 16x = 32Divide 16 on both sides: x = 2Step 3: Solve equation
Define: 8x - 4Substitute: 8(2) - 4Multiply: 16 - 4Subtract: 12And we have our final answer!
If X is an exponential random variable with parameter λ, and c>0, show that cX is exponential with parameter λ/c.CDF Method:Let X be a continuous random variable and let Y=g(X)be a function of that random variable, where g(X) is some function of X. Let fX(x) be the probability density function (PDF) of X and fY(y) be the PDF of Y. Recall that the cumulative distribution function (CDF) of X is defined as the probability that X is less than or equal to some value x, for any real value of x. Mathematically,FX(x)=P(X≤x)Similarly, FY(y)=P(Y≤y).To find the distribution of Y, we can use the CDF method. We start by expressing the CDF of Y (FY(y)) in terms of X. We do this by using the fact that Y=g(X)and then solving the resulting inequality for X. Mathematically,FY(y)=P(Y≤y)=P(g(X)≤y)=⋯=P(X ???⋯)We isolate X in the inequality and we get an inequality which can be changed into CDF terms (the CDF of X).After we find the CDF of Y, we can differentiate it to get the PDF of Y. Recall that for any random variable, the first derivative of its CDF is equal to its PDF. In mathematical terms,fY(y)=ddyFY(y)We do this using the CDF of Y we obtained earlier. After completing this step, you will have the PDF of Y.
Answers
We have shown that cX is exponential with parameter λ/c when X is an exponential random variable with parameter λ and c > 0.
To show that cX is exponential with parameter λ/c when X is an exponential random variable with parameter λ, and c>0, we will use the CDF method:
1. Define the transformation: Let Y = cX be a function of the random variable X, where c > 0.
2. Find the CDF of Y: We want to find P(Y ≤ y), which is equal to P(cX ≤ y) or P(X ≤ y/c).
3. Express CDF of Y in terms of X: Since P(X ≤ y/c) is the CDF of X at y/c, we have FY(y) = FX(y/c).
4. Find the PDF of X: The exponential distribution has the PDF fX(x) = λ * exp(-λx) for x ≥ 0.
5. Differentiate the CDF of Y to find its PDF: To find fY(y), we differentiate FY(y) with respect to y. Using the chain rule, we have:
fY(y) = d(FX(y/c))/dy = fX(y/c) * (1/c)
6. Substitute the PDF of X: Now, we replace fX(y/c) with its exponential form λ * exp(-λ(y/c)):
fY(y) = (λ * exp(-λ(y/c))) * (1/c)
7. Simplify the expression: fY(y) = (λ/c) * exp(-λ(y/c))
This is the PDF of an exponential distribution with parameter λ/c. Therefore, cX is exponential with parameter λ/c when X is an exponential random variable with parameter λ and c > 0.
Learn more about "variable": https://brainly.com/question/82796
#SPJ11