What is the domain of the function y= 2√x-6?

Answer:

6610

Step-by-step explanation:

We have tan(X) = opposite/ adjacent

tan(QBP) = PQ/BQ

tan(35) = PQ/BQ    ---eq(1)

tan(QAP) = PQ/AQ

tan(20) = \(\frac{PQ}{AB +BQ}\)

\(=\frac{1}{\frac{AB+BQ}{PQ} } \\\\=\frac{1}{\frac{AB}{PQ} +\frac{BQ}{PQ} } \\\\= \frac{1}{\frac{230}{PQ} + tan(35)} \;\;\;(from\;eq(1))\\\\= \frac{1}{\frac{230 + PQ tan(35)}{PQ} } \\\\= \frac{PQ}{230+PQ tan(35)}\)

230*tan(20) + PQ*tan(20)*tan(35) = PQ

⇒ 230 tan(20) = PQ - PQ*tan(20)*tan(35)

⇒ 230 tan(20) = PQ[1 - tan(20)*tan(35)]

\(PQ = \frac{230 tan(20)}{1 - tan(20)tan(35)}\)

\(= \frac{230*0.36}{1 - 0.36*0.7}\\\\= \frac{82.8}{1-0.25} \\\\=\frac{82.8}{0.75} \\\\= 110.4\)

PQ = 110.4

≈110

Height above sea level = 6500 + PQ

6500 + 110

= 6610

Answer:

48

Step-by-step explanation:

12*4=48

Answer:

answer= 6

Step-by-step explanation:

if ²/6 means 2 ÷ n

n= 6

The final value of the iterated integral is 945\(\sqrt{10}\).

To calculate the iterated integral, we need to evaluate the inner integral with respect to y first and then the outer integral with respect to x.

The inner integral is to be integrated with respect to y is:

∫(6xy\(\sqrt{(x^2 + y^2)}\))dy from 0 to 1 = [3y(\(x^2 + y^2\)\()^{(3/2)}\))] from 0 to 1

= [3y*\((x^2 + y^2\)\()^{(3/2)}\)] from 0 to 1

= 3(1)*(\(x^2\) + 1\()^{(3/2)}\)

= 3(\(x^2\) + 1\()^{(3/2)}\)

Now, we can use this result as the inside function to evaluate the outer integral with respect to x.

The outer integral is to be integrated with respect to x is:

∫(3(\(x^2\) + 1\()^{(3/2)}\))dx from 0 to 3

= [x(\(x^2\) + 1\()^{(5/2)}\)] from 0 to 3

= [3\((3^2 + 1\) \()^{(5/2)}\) - 0(0^2 + 1\()^{(5/2)}\)]

= [3(10 - 0]

= [945\(\sqrt{10}\))]

So the final value of the iterated integral is 945\(\sqrt{10}\).

Read more about Integrals:

brainly.com/question/20156869

#SPJ4

The complete question is -

Calculate the iterated integral. Integral from 0 to 3 integral from 0 to 1 of 6xy\(\sqrt{(x^2 + y^2)}\) dy dx

Answer:

A: the probability that a 1 is received is 0.56.

B:  the probability that a 0 was sent given that a 1 is received is (2/25) * (1 - P(0 sent)).

Step-by-step explanation:

To solve this problem, we can use conditional probabilities and the concept of Bayes' theorem.

a. To find the probability that a 1 is received, we need to consider the two possibilities: either a 1 was sent and remained unchanged, or a 0 was sent and got flipped to a 1 by the random error.

Let's denote:

P(1 sent) = 0.6 (probability a 1 is sent)

P(0→1) = 0.2 (probability a 0 is flipped to 1)

P(1 received) = ?

P(1 received) = P(1 sent and unchanged) + P(0 sent and flipped to 1)

= P(1 sent) * (1 - P(0→1)) + P(0 sent) * P(0→1)

= 0.6 * (1 - 0.2) + 0.4 * 0.2

= 0.6 * 0.8 + 0.4 * 0.2

= 0.48 + 0.08

= 0.56

Therefore, the probability that a 1 is received is 0.56.

b. If a 1 is received, we want to find the probability that a 0 was sent. We can use Bayes' theorem to calculate this.

Let's denote:

P(0 sent) = ?

P(1 received) = 0.56

We know that P(0 sent) + P(1 sent) = 1 (since either a 0 or a 1 is sent).

Using Bayes' theorem:

P(0 sent | 1 received) = (P(1 received | 0 sent) * P(0 sent)) / P(1 received)

P(1 received | 0 sent) = P(0 sent and flipped to 1) = 0.4 * 0.2 = 0.08

P(0 sent | 1 received) = (0.08 * P(0 sent)) / 0.56

Since P(0 sent) + P(1 sent) = 1, we can substitute 1 - P(0 sent) for P(1 sent):

P(0 sent | 1 received) = (0.08 * (1 - P(0 sent))) / 0.56

Simplifying:

P(0 sent | 1 received) = 0.08 * (1 - P(0 sent)) / 0.56

= 0.08 * (1 - P(0 sent)) * (1 / 0.56)

= 0.08 * (1 - P(0 sent)) * (25/14)

= (2/25) * (1 - P(0 sent))

Therefore, the probability that a 0 was sent given that a 1 is received is (2/25) * (1 - P(0 sent)).

A message is coded into the binary symbols 0 and 1 and the message is sent over a communication channel. The probability a 0 is sent is 0.4 and the probability a 1 is sent is 0.6. The channel, however, has a random error that changes a 1 to a 0 with probability 0.2 and changes a 0 to a 1 with probability 0.1. (a) What is the probability a 0 is received? (b) If a 1 is received, what is the probability a 0 was sent?

Answer:

She wrote 3 pages per hour

Step-by-step explanation:

12 ÷ 4 is 3

48 ÷ 16 is 3

or add the days and hours

16 + 4 = 20

48 + 12 = 60

60 days /20 hours = 3 pages per hour

Answer:

The answer is 2 561,2785 !!!

The required value is 2,556.2785 which is determined by the multiplication operation.

In mathematics, Multiplication operations perform Multiplying values on either side of the operator.

For example 4×2 = 8

The numbers are given in the question, as follows:

78.93 and 32.45

To calculate the product of 78.93 and 32.45, you can use the standard multiplication algorithm.

78.93 x 32.45

Apply the multiplication operation, and we get

2,556.2785

Thus, the required value is 2,556.2785.

Learn more about Multiplication operations here:

brainly.com/question/25834626

#SPJ2

The difference between the actual quotient and the estimated quotient of 54,114 ÷ 29 is approximately 66.3448275862068965517241379.

To find the difference between the actual quotient and the estimated quotient of 54,114 ÷ 29, we need to first calculate the actual quotient and then the estimated quotient.

Actual quotient:

Dividing 54,114 by 29, we get:

54,114 ÷ 29 = 1,866.3448275862068965517241379 (approximated to 28 decimal places)

Estimated quotient:

Rounding the dividend, 54,114, to the nearest thousand gives us 54,000. Rounding the divisor, 29, to the nearest ten gives us 30. Now, we can perform the division with the rounded values:

54,000 ÷ 30 = 1,800

Difference between actual and estimated quotient:

Actual quotient - Estimated quotient = 1,866.3448275862068965517241379 - 1,800 = 66.3448275862068965517241379

For mor such questions on quotient visit:

https://brainly.com/question/11418015

#SPJ8

Answer:

perpindicular

Step-by-step explanation:

The line a and line d are perpendicular to each other.

A perpendicular line is a line that intersect another line at 90 degrees. Perpendicular lines are also called normal lines.

After constructing the two lines; line a and line intersect or meet each other at 90 degrees to the horizontal.

Thus, we can conclude that the line a and line d are perpendicular to each other.

Learn more about perpendicular lines here: https://brainly.com/question/1202004

Answer:

105-30-45-3028+10000000000000038492= 1.000000000000003e19

Step-by-step explanation:

I did the math

have a good day!!

The sequence -19, -11, -3, 5,... is arithmetic with a common difference of 8.

An arithmetic sequence is a sequence of numbers in which each term is obtained by adding a constant value, called the common difference (d), to the preceding term. To determine if the given sequence is arithmetic, we can find the differences between consecutive terms.

The difference between the second and first terms is 11 - (-19) = 30, and the difference between the third and second terms is -3 - (-11) = 8. The difference between the fourth and third terms is 5 - (-3) = 8. Since the differences between consecutive terms are the same, the sequence is arithmetic.

The common difference can be found by subtracting any term from the term that follows it. For example, the common difference can be obtained by subtracting the second term (-11) from the third term (-3), or by subtracting the third term (-3) from the fourth term (5).

In both cases, we get a common difference of 8. Therefore, the common difference of the given sequence is 8.

For more information regarding arithmetic sequence, click below:
https://brainly.com/question/28583639#

Answer:

Maybe 3 because 2*9=x+15

So 18=x+15

So x=3

Am not sure

Answer:

3 because 2*9=x+15

So 18=x+15

So x=3

Step-by-step explanation:

The probability of randomly selecting a number between 1 and 1000 (including both ends) which is divisible by 3, 3 and 5, and 3 or 5 is 33.3%, 6.6%, and 46.7%, respectively.

To find the probability of randomly selecting a number between 1 and 1000 (including both ends), we can count the number of the desired outcomes and divide it by the total number of possible outcomes.

a. To find the probability of randomly selecting a number between 1 and 1000 (including both ends) which is divisible by 3, we can count the number of multiples of 3 between 1 and 1000, and divide by the total number of possible outcomes.

The first multiple of 3 is 3, and the last multiple of 3 that is less than or equal to 1000 is 999.

999/3 = 333

So there are 333 multiples of 3 between 1 and 1000.

probability = 333/1000 = 0.333 = 33.3%

b. To find the probability of randomly selecting a number between 1 and 1000 (including both ends) which is divisible by 3 and 5, we can count the number of multiples of 15 (the least common multiple of 3 and 5) between 1 and 1000, and divide by the total number of possible outcomes.

The first multiple of 15 is 15, and the last multiple of 15 that is less than or equal to 1000 is 990.

990/15 = 66

So there are 66 multiples of 15 between 1 and 1000.

probability = 66/1000 = 0.066 = 6.6%

c. To find the probability of randomly selecting a number between 1 and 1000 (including both ends) which is divisible by 3 or 5, we can count the number of multiples of 3 or 5 (or both) between 1 and 1000, and divide by the total number of possible outcomes.

To count the number of multiples of 3 or 5, we can add the number of multiples of 3 and the number of multiples of 5, and then subtract the number of multiples of 15 (to avoid double-counting).

The number of multiples of 3 between 1 and 1000 is 333, the number of multiples of 5 is 200, and the number of multiples of 15 is 66.

probability = (200 + 333 - 66)/1000 = 0.467 = 46.7%

Learn more about probability here: https://brainly.com/question/24756209

#SPJ4

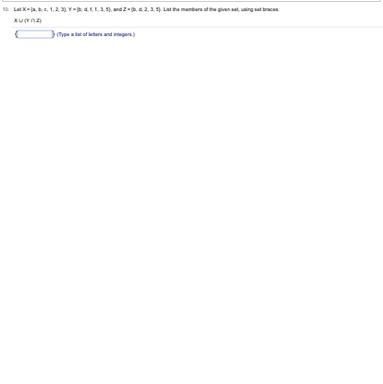
The members of the given set in this problem are given as follows:

X U (Y ∩ Z) = {p, q, r, 0, 6, 21, 22, 23, 26}

The union and intersection sets of multiple sets are defined as follows:

The intersection of the sets Y and Z for this problem is given as follows:

Y ∩ Z = {0, 6, 23, 26}

(which are the elements that belong to both of the sets).

The union of the above set with the set X is given as follows:

X U (Y ∩ Z) = {p, q, r, 0, 6, 21, 22, 23, 26}

(elements that belong to at least one of the sets).

More can be learned about union and intersection at brainly.com/question/4699996

#SPJ1

We have a total of seven 4-tuples that satisfy the given relation.The given relation is {(a,b,c,d) | a,b,c,d∈!+ , a+b+c+d = 6}. It can be understood as the set of 4-tuples (a, b, c, d) such that a, b, c, and d are positive integers and their sum is equal to 6.

Let's now list all the possible 4-tuples that satisfy the given relation. The possible combinations are as follows: (1, 1, 1, 3), (1, 1, 2, 2), (1, 2, 1, 2), (2, 1, 1, 2), (1, 2, 2, 1), (2, 1, 2, 1), and (2, 2, 1, 1).

Here's a brief explanation on how these 4-tuples were obtained. Let a, b, c, and d be positive integers such that a+b+c+d = 6. The least possible value that each variable can take is 1.

So, we start with a=1 and find all possible values of (b, c, d) that satisfy the given equation. Then, we move to a=2 and repeat the process. Finally, we list all the possible 4-tuples that we obtained.

Thus, we have a total of seven 4-tuples that satisfy the given relation.

For more question on integers

https://brainly.com/question/929808

#SPJ8

Answer:

no. a function doesnt contain an = sign

Step-by-step explanation:

Answer:

Yes, it is a function.

Explanation:

xy + 6y = 9

y(x + 6) = 9

y = 9/(x + 6)

It is a inverse variation function.

Where equation: xy = k               ["k" is constant]

Answer:

2 1 ÷ 2

Step-by-step explanation:

Given that

The kitchen of Amita would be a rectangular area contains 3 and 3 ÷ 4 square meters

And, the width of her kitchen is 1 and 1 ÷ 2 meter

So based on the above information, the length of Amita kitchen is

Here you divide the rectangular area by the width

= (3 and 3 ÷ 4) ÷ (1 and 1 ÷ 2)

= 2 and 1 ÷ 2

Hence, the  length in meters of Anita's kitchen is  2 and  1 ÷ 2  

Using the formula for finding area of a rectangle we can get the area of the shaded region = 106 sq. meters.

The formula for calculating a rectangle's area can be used to determine how much space the rectangle takes up within its perimeter. The area of a rectangle is determined by multiplying its length by its width (breadth). The following formula can be used to get the area of a rectangle whose length and breadth are "l" and "w," respectively. L * W = the rectangle's area. Hence, the area of a rectangle is equal to length × width

Here, in the given figure, area of the small rectangle =

length × breadth

= 7 × 2

= 14 sq. meters

Now area of the shaded region =

12 × 10

=120 sq. meters.

Therefore, area of the shaded region = 120 - 14

= 106 sq. meters

To know more about area of rectangle, visit:

https://brainly.com/question/16309520

#SPJ1

Answer:

Step-by-step explanation:

The thousand mark is the 4th number when going from right to left. So it would be the {6},976. When it comes to rounding, you go "5 and above, give it a shove, 4 and below, let it go. 6,976 rounded to the nearest thousand is 7,000,  3,983 rounded to the nearest thousand is 4,000,  13,560 rounded is 14,000.

7,000 + 4,000+ 14,000 = 25,000

Answer:

D) $247.90

Step-by-step explanation:

\( \underline{\sf{y = 2.44x + 3.90}}\)

y is the dependent function whereas x is the independent function.

(What does this mean?)

The values of y depend on the values of x, I.e., any change in the value of x causes a change in the value of y, meanwhile, the opposite doesn't happen.

The cost to print the invitation depends on the number of invitations, for real.

The question asks us to find the cost of printing 100 invitations.

Substituting x for 100:

y = (2.44 × 100) + 3.90

y = 244 + 3.90

y = 247.90

The value of y obtained for x = 100 is the cost of printing 100 invitations – $ 247.90

Answer:

x=12

Step-by-step explanation:

Simplifying

30 + 4x + 2 = 8 + 6x

Reorder the terms:

30 + 2 + 4x = 8 + 6x

Combine like terms: 30 + 2 = 32

32 + 4x = 8 + 6x

Solving

32 + 4x = 8 + 6x

Solving for variable 'x'.

Move all terms containing x to the left, all other terms to the right.

Add '-6x' to each side of the equation.

32 + 4x + -6x = 8 + 6x + -6x

Combine like terms: 4x + -6x = -2x

32 + -2x = 8 + 6x + -6x

Combine like terms: 6x + -6x = 0

32 + -2x = 8 + 0

32 + -2x = 8

Add '-32' to each side of the equation.

32 + -32 + -2x = 8 + -32

Combine like terms: 32 + -32 = 0

0 + -2x = 8 + -32

-2x = 8 + -32

Combine like terms: 8 + -32 = -24

-2x = -24

Divide each side by '-2'.

x = 12

Simplifying

x = 12

Answer:

108 cm that my answer

sana makatulong

The answer is 508.9 cubed

108cm cubed is wrong

Answer:

Step-by-step explanation:

(-4 -7)/(-6+4)= -11/2

y + 4 = -11/2(x + 6)

y + 4 = -11/2x - 33

y = -11/2x - 37

AI initially had 786,432 pennies.

We have,

Let P be the initial number of pennies AI had.

According to the problem:

AI gives 3/8 of P pennies to Bev.

Bev gives 3/8 of what she got from AI to Carl.

Carl gives 3/8 of what he got from Bev to Dani.

Set up an equation to solve for P.

Let's start by finding how many pennies Dani gets from Carl:

Carl gives 3/8 of what he got from Bev to Dani, so Dani gets:

(3/8) x (3/8) x (3/8) x P pennies from Carl.

Next, let's find how many pennies Carl gets from Bev:

Bev gives 3/8 of what she got from AI to Carl,

So Carl gets (3/8) x (3/8) x P pennies from Bev.

Now we can substitute this expression for the number of pennies Carl gets from Bev into the expression for the number of pennies Dani gets from Carl:

Dani gets (3/8) x (3/8) x (3/8) x P pennies from Carl = (3/8) x (3/8) x (3/8) x (3/8) x P pennies from Bev =  (3/8) x (3/8) x (3/8) x (3/8) x (3/8) x P pennies from AI.

We know that Dani gets 378 pennies, so we can set this expression equal to 378 and solve for P:

(3/8) x (3/8) x (3/8) x (3/8) x (3/8) x P = 378

Simplifying this expression:

P = 378 x (8/3) x (8/3) x (8/3) x (8/3) x (8/3)

P = 786,432

Therefore,

AI initially had 786,432 pennies.

Learn more about expressions here:

https://brainly.com/question/3118662

#SPJ1

Answer:

4:14 or 2:7

Step-by-step explanation:

there are 4 girls and 14 boys

the ratio is 4:14

correct me if this is wrong

Answer:

2/7

Step-by-step explanation:

two find the answer you need to reduce 4 and 14 into the lowest common denominator.

Answer:

$35,000

Step-by-step explanation:

In a proposed business venture, Serena estimates that there is a 65% chance that she will make $70,000

And also a 35% chance that she will loose $30,000

Therefore the expected value can be calculated as follows

E= 65/100 × 70,000 + 35/100 × (-30,000)

= 0.65 × 70,000 + 0.35(-30,000)

= 45,500 - 10,500

= $35,000

Hence the expected value is $35,000

Based on the probability of the payoffs, we can calculate that the expected value is $35,000.

The expected value is calculated as:

= ∑(Probability of payoff x Payoff)

The expected value here is therefore:

= (65% x 70,000) + (35% x -30,000)

= 45,500 - 10,500

= $35,000

In conclusion, the expected value is $35,000.

Find out more at https://brainly.com/question/15554351.