What is the area of the triangle below?
what is the area of the triangle below?

Answers
Answer:
Step-by-step explanation:
I can't add a answer because I see any problem.
The value of area of the triangle is, 5 units²
What is mean by Triangle?A triangle is a three sided polygon, which has three vertices and three angles which has the sum 180 degrees.
Given that;
Triangle is shown in image.
Now, We get;
When we measure we have to get;
Base = 5 units
Height = 2 units
We know that;
Area of triangle = 1/2 x base x height
= 1/2 x 5 x 2
= 5 units²
Thus, The value of area of the triangle is, 5 units²
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ7
Related Questions
HELP ME FINAL GRADE QUESTION!!!!
Sammi wants to join a gym. Gym A costs $33.60 plus an additional $5.45 for each visit. Gym B has no initial fee but costs $8.25 for each visit. After how many visits will both plans cost the same?
Answers
The solution is :
After 3 visits both plans will cost the same.
Here, we have,
Gym A costs $26.76 plus an additional $4 for each visit.
Gym B has no initial fee but costs $12.92 for each visist.
The cost for gym A can be written as
C= $26.76 + 4(x) where x is the number of visits to the gym A
The cost for gym B can be written as
C= $12.92 (x) where x is the number of visits to the gym B
Both costs will be equal
12.92x= 26.76 +4x
12.92x-4x= 26.76
8.92x= 26.76
x= 26.76/8.92
x= 3
after 3 visits both plans will cost the same.
Check
12.92x= 26.76 +4x
12.92*3= 26.76 +12
38.76= 38.76
To learn more on multiplication click:
brainly.com/question/5992872
#SPJ1
complete question:
Carmen wants to join a gym. Gym A costs $26.76 plus an additional $4 for each visit. Gym B has no initial fee but costs $12.92 for each visit. After how many visits will both plans cost the same?
leon lowers his net into the water 10 feet below sea level. He raises the net out of the water 2 feet above sea level. What is the difference between the lowest level and the highest level?
Answers
Answer:
8
Step-by-step explanation:
10 is the lowest , and 2 is the highest, so you would subtract 2 from 10 and get 8
need help asap
solve for x using cross multiplication 5x over 7= 2x over 3

Answers
Answer:
0.4
step-by-step explanation
5x times 3 = 7 times 2x-4
first, you divide both sides by 2x
2.5x times 3 = 7-4
then, divide both sides by three
2.5x = 1
lastly, divide both sides by 2.5
x = 0.4
Simplify the radical expression.
Answers
To simplify a radical expression, we aim to simplify the radical itself by finding perfect square factors and then simplify any remaining factors outside the radical.
Step 1: Identify perfect square factors: Look for any factors inside the radical that are perfect squares. A perfect square is a number that can be expressed as the square of an integer.Step 2: Simplify the perfect square factors: Take the square root of the perfect square factors and bring them out of the radical. For example, if you have √(4x^2), you can simplify it as 2x because 4 is a perfect square and its square root is 2.Step 3: Simplify any remaining factors: If there are any remaining factors inside the radical that are not perfect squares, leave them under the radical.Step 4: Combine the simplified factors: Multiply the factors outside the radical together and write them alongside any remaining factors inside the radical.For example, if you have the expression √(12x^3), you can simplify it as follows:
√(12x^3) = √(4 * 3 * x^2 * x) = 2x√(3x)
So the simplified form of √(12x^3) is 2x√(3x).
By following these steps, you can simplify radical expressions and write them in a more simplified and concise form.
Learn more about radical expression here : brainly.com/question/28336985
#SPJ11
Find the value of z.

Answers
2z = 15
z = 7.5
y(2.5+7)+y-2
10.5y-2
which statement best explains why the expressions are equivalent
a the expressions have the same value for any value of y
b the expressions have the same value for only whole number values of y
c the expressions have the same value only when y is an odd number.
d the expressions have the same value only when y is an even number.
Answers
Using the equivalence concept, it is found that the correct option is given by:
a the expressions have the same value for any value of y.
What are equivalent expressions?Two expressions are said to be equivalent if for the same input, they have the same value.
In the expressions given in this problem, the input is y, hence they have the same value for any value of y, which means that option A is correct.
More can be learned about equivalent expressions at https://brainly.com/question/2972832
For each table, calculate the mean weight for each group, xa and xb, and find the difference of the mean
of group a and the mean of group b (xa - xb).
Answers
The mean weight for each group and the difference between them, calculate the mean weight for group a and group b separately, and then subtract the mean of group b from the mean of group a.
To calculate the mean weight for each group (xa and xb), follow these steps:
1. Add up all the weights of group a and divide by the total number of data points in group a to find the mean weight (xa).
2. Repeat the same process for group b, adding up all the weights and dividing by the total number of data points to find the mean weight (xb).
3. Finally, subtract the mean of group b (xb) from the mean of group a (xa) to find the difference between the two means (xa - xb).
In summary, to find the mean weight for each group and the difference between them, calculate the mean weight for group a and group b separately, and then subtract the mean of group b from the mean of group a.
To know more about mean visit:
https://brainly.com/question/31101410
#SPJ11
Given the function f(x)=-(\sqrt(x))/(5) +(5\sqrt(x^(3)))/(6) find f'(4) Express your answer as a single fraction in simplest form.
Answers
\(f'(4) = (-1 + 20√(2))/20\) is the required solution.
Given the function
\(f(x) = -√(x)/5 + (5√(x³))/6\).
We have to find the value of f'(4) and express our answer as a single fraction in its simplest form.
So, let's start with the solution:
First, we will calculate f'(x) using the derivative formula.
\(f'(x) = -1/5(1/2)(x^(-1/2)) + (15/6)(1/2)(x^(3/2))(x^2)\)
[Applying the power rule and the chain rule] Simplifying \(f'(x)\), we get;
\(f'(x) = (-1/10)(1/√(x)) + (5/2)x^(5/2)\)
Therefore,
\(f'(4) = (-1/10)(1/√(4)) + (5/2)(4^(5/2))\)
⇒\(f'(4) = (-1/20) + 40√(2)/2\) [Simplifying the expression]
⇒\(f'(4) = (-1/20) + 20√(2)\)
⇒\(f'(4) = (-1 + 20√(2))/20\)
Therefore,
\(f'(4) = (-1 + 20√(2))/20\) is the required solution.
To know more about derivative visit:
https://brainly.com/question/29144258
#SPJ11
Vocab in your own words:
How to add two positive integers:
How to add two negative integers:
How to add a positive and a negative integers:
Answers
How to add two positive integers:
You add the numbers like you normally would. There's no trick even though it seems like a trick question.
Example: 3+5 = 8
In that example, you can think of like starting at 3 on the number line. Then you move 5 units to the right to arrive at 8 on the number line.
-----------------------------------------------------
How to add two negative integers:
Treat the negative numbers as their positive version of themselves. Next, you add those positive counterparts like normal. The last thing you do is make the result negative.
For example,
-9 + (-12) = -21
which we can think of like this
9+12 = 21
Then we just make everything negative to get that first equation mentioned.
-----------------------------------------------------
How to add positive and negative integers:
This will depend on which has larger absolute value. In other words, which is further away from 0 on the number line.
In any event, you basically subtract the positive version of each number. Then the one furthest from 0 will determine if the result is positive or negative.
Examples:
-8 + 9 = 1
7 + (-12) = -5
In the first example, we can think of it like 9-8 = 1. I'm subtracting the two numbers 8 and 9, but doing so large - small and only focusing on the positive versions so far. Because 9 is further away from 0 compared to -8, this ultimately means the result is positive (since 9 is positive).
In the second example, we would say 12-7 = 5. Then note how -12 is farther away from 0 compared to 7. This means the negative side wins, so to speak, and the final result is negative.
(a) Give pseudocode for an algorithm that finds the first repeated integer in given a sequence of integers. (b) Analyze the worst-case time complexity of the algorithm you devised in part (a).
Answers
(a) Pseudocode for the algorithm that finds the first repeated integer in a given sequence of integers is as follows:
1. Initialize an empty set called "visited".
2. Traverse the given sequence of integers.
3. For each integer in the sequence, check if it is already in the "visited" set.
4. If the integer is in the "visited" set, return it as the first repeated integer.
5. Otherwise, add the integer to the "visited" set.
6. If there is no repeated integer, return "None".
(b) The worst-case time complexity of the algorithm is O(n), where n is the length of the sequence of integers.
Therefore, the time complexity of the algorithm increases linearly with the size of the input sequence.
Read more about the Pseudocode.
https://brainly.com/question/17442954
#SPJ11
Suppoe that the height of the population in two countrie i normally ditributed with tandard deviation =21cm. The average adult male height in the firt country i 170cm. We upect that the men in the econd country might have a different average height due to ome environmental factor. We pick a random ample ize of 9 from the adult male in the econd country and obtain that the average height of thi ample i 165. 8 cm. Given the data: Do you reject or not the affirmation that the real average height in the econd country i different to 170cm?
Answers
The real average is height in second country is less than 170, therefore real average height is different in both the countries.
#SPJ4
Two containers designed to hold a water our side-by-side, both in the shape of a cylinder. Container a has A diameter of 6 feet and a height of 15 feet. Container b has a diameter of 8 feet and a height of 10 feet. Container is full of water in the water is pumped into container be until container is empty. After the pumping is complete what is the volume of the empty portion of container b, to the nearest 10th of a cubic foot
Answers
Answer:
78.5 ft3
Step-by-step explanation:
First we need to find the volume of both containers.
The volume of a cylinder is given by the equation:
Volume = pi * diameter^2 * height / 4
If cylinder A has a diameter of 6 feet and height of 15 feet, we have:
Volume_A = pi * 6^2 * 15 / 4 = 424.115 ft3
If cylinder B has a diameter of 8 feet and height of 10 feet, we have:
Volume_A = pi * 8^2 * 10 / 4 = 502.6548 ft3
After pumping the water from A to B, the volume of the empty portion of B will be the difference of their volumes:
Volume_B - Volume_A = 502.6548 - 424.115 = 78.5398 ft3
Rounding to the nearest 10th of a cubic foot, we have a difference of 78.5 ft3
Brainliest and 25 points for solving these

Answers
The value that make the function continuous everywhere are:
7. k = 1/98. c = -1 + k9. a = 10 - π and b = π10. b = π/2.How to determine functions that are continuous everywhere?To find the values of a, b, and c that make the given functions continuous everywhere, ensure that the function values from the left and right sides of the points of discontinuity match.
For f(x) = kx², x ≤ 3; 4x - 11, x > 3:
Two parts of the function to agree at x = 3,
Solving for k:
k(3)² = 4(3) - 11
9k = 12 - 11
9k = 1
k = 1/9
Therefore, the value of k that makes the function continuous everywhere is k = 1/9.
For g(x) = cx², x < 1; 4, x = 1; -x³ + kx, x > 1:
Two parts of the function to agree at x = 1.
Solving for c:
c(1)² = -1³ + k(1)
c = -1 + k
Therefore, the value of c that makes the function continuous everywhere is c = -1 + k.
For h(x) = π, x < 0; x² + ax + b, 0 ≤ x ≤ 1; 6x + 5, x > 1:
Three parts of the function to agree at their boundaries.
Solving for a and b:
0² + a(0) + b = π
b = π
1² + a(1) + b = 6(1) + 5
1 + a + π = 6 + 5
a = 10 - π
Therefore, the values of a and b that make the function continuous everywhere are a = 10 - π and b = π.
For f(x) = x², x < 1; sin(bx), x ≥ 1:
Two parts of the function to agree at x = 1.
Setting them equal and solving for b:
1² = sin(b(1))
1 = sin(b)
Therefore, the value of b that makes the function continuous everywhere is b = π/2.
Find out more on function here: https://brainly.com/question/30487025
#SPJ1
It was discovered that 85% of yale college students finish their course of study during the require time. In a group of 5 students find the probability.A) 2 students finish their course on time.:
Answers
In a group of five students of Yale college
a) The probability that two students finish their course on time is equals to the 0.0243843.
b) Probability that less than 2 students finish their course on time is equals to the
0.002227.
The probability that college students finish their course of study during the require time = 85% = 0.85
Number of students in a group= 5
The probability that college students finish their course of study during the require time = 85% = 0.85
Number of students in a group= 5
We have to determine the probability that 2 students finish their course on time.
Binomial Probability distribution formula,P( X= x) = ⁿCₓ (p)ˣ (1 - p)⁽ⁿ⁻ˣ⁾, where
p--> probability of getting success in one trial
n --> number of trials
x --> number of success desired
ⁿCₓ --> number of combinations
Here, n = 5, p = 0.85, x = 2
a) The probability that 2 students finish their course on time, P(X = 2)
= ⁵C₂ (0.85)²(1 - 0.85)³
= 10(0.85)²(0.15)³
= 0.0243843
b) Probability that less than 2 students finish their course on time is, P(X < 2)
= P(X = 0) + P(X = 1) = ⁵C₀ (0.85)⁰(1 - 0.85)⁵ + ⁵C₁ (0.85)¹(1 - 0.85)⁴
= 0.0022275
Hence, required probability is 0.002227.
For more information about binomial probability distribution, visit:
https://brainly.com/question/14984348
#SPJ4
Complete question:
It was discovered that 85% of yale college students finish their course of study during the require time. In a group of 5 students find the probability.
a) 2 students finish their course on time.
b) less than 2 students finish their course on time.
#SPJ4
In space, how many planes can be perpendicular to a given line at a given point on that line in space?
A. 1
B.0
C. 3
D. infinitely many
Answers
In space, there can be infinitely many planes that are perpendicular to a given line at a given point on that line.
The correct answer is Option D.
The key concept here is that a plane is defined by having at least three non-collinear points.
When a line is given, we can choose any two points on that line, and then construct a plane that contains both the line and those two points. By doing so, we ensure that the plane is perpendicular to the given line at the chosen point.
Since we can select an infinite number of points on the given line, we can construct an infinite number of planes that are perpendicular to the line at various points.
Thus, the correct answer is D. infinitely many planes can be perpendicular to a given line at a given point in space.
The correct answer is Option D.
For more such questions on perpendicular
https://brainly.com/question/1202004
#SPJ8
A recipe uses 5 cups of milk to make 30 servings. If the same amount of milk is used for each serving, how many servings can be made from one quart?
1 gallon = 4 quarts, 1 quart = 2 pints, 1 pint = 2 cups, 1 cup = 8 fluid ounces
Before you try that problem, answer the question below.
How many cups will you need to find the number of servings for?
Answers
Answer:
is 6 a choice if so that is the correct answer:)
Step-by-step explanation:
bc ik
Answer:
For the first part the answer is we will to find the number of servings for 8 cups.
The second and finnal answer is 16 servings
Step-by-step explanation:
2 quarts x 2 = 4 pints x 2 = 8 cups
5 cups per 10 servings unit rate is 1:2 X 8 = 8:16, Therfore 16 servings.
Glad I could help! :)
find the average value of f over the given rectangle. f(x, y) = 4ey x ey , r = [0, 6] ⨯ [0, 1] fave =
Answers
The average value of f over the rectangle R is 6(e2 - 1).
To find the average value of the function f(x, y) = 4ey x ey over the rectangle R = [0, 6] ⨯ [0, 1], we need to calculate the double integral of f over R and divide it by the area of R:
fave = (1/area(R)) ∬R f(x, y) dA
where dA denotes the area element in the xy-plane.
First, we can simplify the expression for f(x, y) by using the properties of exponentials:
f(x, y) = 4ey x ey = 4e2y x
Now we can evaluate the integral:
f_ave = (1/area(R)) ∬R f(x, y) dA
= (1/(6*1)) ∫[0,6] ∫[0,1] 4e2y x dy dx
= (1/6) ∫[0,6] 4x ∫[0,1] e2y dy dx
= (1/6) ∫[0,6] 4x [e2y/2]0¹ dx
= (1/6) ∫[0,6] 2x (e2 - 1) dx
= (1/3) (e2 - 1) ∫[0,6] x dx
= (1/3) (e2 - 1) [(6²)/2]
= (18/3) (e2 - 1)
= 6(e2 - 1)
For more about average value:
https://brainly.com/question/30858174
#SPJ4
Let f(x, y, z) = = x² + y² + z² The mixed third partial derivative, -16xyz (x² + y² + z²)4 -24xyz (x² + y² + z²)4 -32xyz (x² + y² + z²)4 -48xyz (x² + y² + z²)4 a³ f əxəyəz' , is equal to
Answers
The mixed third partial derivative of the function f(x, y, z) = x² + y² + z² with respect to x, y, and z is equal to -48xyz(x² + y² + z²)^4.
To find the mixed third partial derivative of the function f(x, y, z) = x² + y² + z² with respect to x, y, and z, we differentiate the function three times, considering each variable separately.
First, let's find the partial derivative with respect to x:
∂/∂x (x² + y² + z²) = 2x.
Next, the partial derivative with respect to y:
∂/∂y (x² + y² + z²) = 2y.
Finally, the partial derivative with respect to z:
∂/∂z (x² + y² + z²) = 2z.
Now, taking the mixed partial derivative with respect to x, y, and z:
∂³/∂x∂y∂z (x² + y² + z²) = ∂/∂z (∂/∂y (∂/∂x (x² + y² + z²))) = ∂/∂z (2x) = 2x.
Since we have the factor (x² + y² + z²)^4 in the expression, the final result is -48xyz(x² + y² + z²)^4.
To know more about partial derivatives click here: brainly.com/question/28750217
#SPJ11
ASAP PLEASE !!! When using a counterexample to prove a conditional statement false, which must be true about the counterexample?
1. There must be infinite counterexamples.
2. The counterexample must satisfy the hypothesis of the conditional statement.
3. There must be at least one example under which the conditional statement is true.
4. The counterexample must satisfy the conclusion of the conditional statement.
Answers
The true statement about the counterexample is;
''The counter example must satisfy the hypothesis of the conditional statement.''
The option (2) is correct.
Here;
To prove a conditional statement false we use a counterexample.
We have to write the true statement about the counterexample.
What is Counterexample?
A counterexample is an example in which the hypothesis is true, but the conclusion is false.
Now,
Since, A counterexample is used to prove a conditional statement to be false.
So, To prove a statement to be false, only one counterexample is sufficient.
And, When using a counterexample to prove a conditional statement false.
Then, The counterexample must satisfy the hypothesis of the conditional statement.
Therefore, The true statement about the counterexample is;
''The counterexample must satisfy the hypothesis of the conditional statement.''
Hence, The option (2) is correct.
Learn more about Counterexample at:
https://brainly.com/question/13482721
#SPJ1
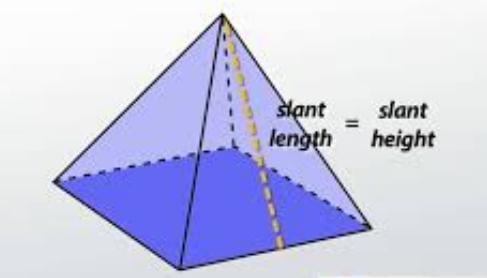
The diagram shows the net of a square pyramid and its dimensions. A net of a square pyramid. The square base has a base and height of 6 feet. There are four triangles that have a base of 6 feet and a height of 4 feet. What is the total surface area of the pyramid in square feet? Record your answer in the box.
Answers
A net of a square pyramid. The square base has a base and height of 6 feet. There are four triangles that have a base of 6 feet and a height of 4 feet.
To find the total surface area of the pyramid, we need to find the area of each of the five faces and then add them up.
The area of the square base is
6 ft x 6 ft = 36 sq ft
Each of the four triangular faces has an area of
(1/2) x base x height = (1/2) x 6 ft x 4 ft = 12 sq ft
So the total area of the four triangular faces is
4 x 12 sq ft = 48 sq ft
Finally, we need to find the area of the fifth face, which is the bottom of the pyramid. Since it is also a square with side length 6 ft, its area is
6 ft x 6 ft = 36 sq ft
Therefore, the total surface area of the pyramid is
36 sq ft (square base) + 48 sq ft (four triangular faces) + 36 sq ft (bottom) = 120 sq ft.
\(\left[\begin{array}{ccc}\1120 square feet\\\end{array}\right]\)
Therefore, the total surface area of the pyramid is 120 square feet.
To know more about square pyramid here
https://brainly.com/question/27681171
#SPJ1
What is the value of a in the equation? 22 = startfraction a over 11 endfraction 2 33 222 242
Answers
Answer:
D / 242
Step-by-step explanation:
hope this helps!
Help me plssss
I’ll give the the brainliest thingy

Answers
The figure is a parallelogram.
True false
Answers
Answer:
Which picture?
Step-by-step explanation:
Also I am guessing false but I don't see the picture
f(x) = -(x + 4)2.4
What is it equivalent to?
Answers
Answer:
−2.4x−9.6
Step-by-step explanation:
2
3
2
x
=2
5
x=
PLEASE HELPPPPPP
Answers
Answer: can you put it in diffrent form beucase the way you have it is really confusing me thanks
Step-by-step explanation:
mandy is watching a space shuttle launch from an observation spot 8 miles away. find the angle of elevation from mandy to the space shuttle, which is at a height of 0.8 miles.
Answers
Angle of elevation from Mandy to the space shuttle, The tangent function relates the angle of elevation to the opposite and adjacent sides of a right triangle. The angle of elevation is 5.71 degrees.
In this scenario, the height of the space shuttle acts as the opposite side and the distance from Mandy to the shuttle acts as the adjacent side of the right triangle.Given that the height of the shuttle is 0.8 miles and the distance from Mandy to the shuttle is 8 miles, we can use the tangent function:
tangent(angle) = opposite/adjacent
tangent(angle) = 0.8/8 Simplifying the equation, we get: tangent(angle) = 0.1 To find the angle itself, we need to take the inverse tangent (arctan) of both sides: angle = arctan(0.1)
Using a calculator, the approximate value of the angle is 5.71 degrees.Therefore, the angle of elevation from Mandy to the space shuttle is approximately 5.71 degrees.
To learn more about angle of elevation click here : brainly.com/question/29008290
#SPJ11
four treatments for fever blisters were randomly assigned to 14 patients the data below shows the number of days from initial appearance of the blisters until healing is complete for each treatment: treatment number of days (a) write the model of the one-way anova for the given data: (1 mark) (b) identify the independent and dependent variables: (2 marks) (c) construct an anova table: (12 marks) (d) based on the study, can we conclude that there is no difference between the four treatments with respect to healing time at 0.5% level of significance? (5 marks)
Answers
The model for data is μ + τ + ε. Independent variable: Treatment, Dependent variable: Number of days until healing is complete. An anova table is given. The value of F-ratio is -10.72 is negative and the mean squares within treatments (MSW) is negative.
To solve the given problem, we need to perform the one-way ANOVA analysis using the provided data. Let's go through the steps
(a) The model of the one-way ANOVA for the given data:
Number of days = μ + τ + ε
where μ is the overall mean, τ represents the treatment effect, and ε is the random error.
(b) The independent variable is the treatment (A, B, C), and the dependent variable is the number of days from initial appearance of the blisters until healing is complete.
(c) Constructing the ANOVA table:
First, calculate the necessary values:
Treatment A: Number of days (5, 8, 7, 7)
Mean (μA) = (5 + 8 + 7 + 7) / 4 = 6.75
Treatment B: Number of days (4, 6, 6, 6, 3, 3)
Mean (μB) = (4 + 6 + 6 + 6 + 3 + 3) / 6 = 4.67
Treatment C: Number of days (6, 4, 5)
Mean (μC) = (6 + 4 + 5) / 3 = 5
Overall mean (μ) = (6.75 + 4.67 + 5) / 3 = 5.81
Next, calculate the sum of squares (SS)
SSA = 4 * (6.75 - 5.81)² + 6 * (4.67 - 5.81)² + 3 * (5 - 5.81)² = 10.08
SST = 4 * (5 - 5.81)² + 6 * (6 - 5.81)² + 3 * (5 - 5.81)² = 4.92
SSW = SST - SSA = 4.92 - 10.08 = -5.16 (negative value due to small sample sizes)
Next, calculate the degrees of freedom (df)
dfA = k - 1 = 3 - 1 = 2
dfT = N - 1 = 14 - 1 = 13
dfW = dfT - dfA = 13 - 2 = 11
Next, calculate the mean squares (MS)
MSA = SSA / dfA = 10.08 / 2 = 5.04
MSW = SSW / dfW = -5.16 / 11 = -0.47 (negative value due to small sample sizes)
Finally, calculate the F-ratio
F = MSA / MSW = 5.04 / -0.47 = -10.72 (negative value due to small sample sizes)
(d) Based on the study, we cannot conclude whether there is a difference between the four treatments with respect to healing time at the 0.5% level of significance because the F-ratio value is negative and the mean squares within treatments (MSW) is negative.
These indicate issues with the data and violate the assumptions of the ANOVA test. Further investigation or additional data may be necessary.
To know more about F-ratio:
https://brainly.com/question/31827066
#SPJ4
--The given question is incomplete, the complete question is given below " table value is given Treatment A Number of days 5 8 7 7. Treatment B Number of days 4 6 6 6 3 3. Treatment C Number of days 6 4 5 . Treatment D Number of days 7 4 6.
Four treatments for fever blisters were randomly assigned to 14 patients. The data above shows the number of days from initial appearance of the blisters until healing is complete for each treatment. (a) Write the model of the one-way ANOVA for the given data. (1 Mark) (b) Identify the independent and dependent variables. (2 Marks) (c) Construct an ANOVA table. (12 Marks) (d) Based on the study, can we conclude that there is no difference between the four treatments with respect to healing time at 0.5% level of significance? (5 Marks)"--
Pythagorean Theoarem:
Answers
The pythagorean theorem is expressed as
hypotenuse^2 = one leg^2 + other leg^2
From the diagram,
hypotenuse = x
one leg = 40
other leg = 9
Thus, we have
\(\begin{gathered} x^2=40^2+9^2 \\ x^2\text{ = 1600 + 81 = 1681} \\ x\text{ = }\sqrt[]{1681} \\ x\text{ = 41} \end{gathered}\)The correct option is B
What is a fraction form of $1.80?
Answers
Answer:Okay, so the first thing to do here is show you that any number can be a fraction if you use a 1 as the denominator. Take a look:
1.80
1
What we really want to do though, is get rid of the decimal places completely so that the numerator in our fraction is a whole number. To do this, we have to count the numbers after the decimal point, which in this case is 80.
To get a whole fraction we need to multiply both the numerator and the denominator by 10 if there is one number after the decimal point, 100 if there are two numbers, 1,000 if it's three numbers and 10,000 if it's...well, you get the idea!
In our case 80 is 2 digits long so we need to multiply the numerator and denominator by 100.
Now we just need to do that multiplication to get our whole fraction:
1.80 x 100
1 x 100
=
180
100
The next step is to simplify this fraction and, to do that, we need to find the greatest common factor (GCF). This is sometimes also known as:
Greatest Common Divisor (GCD)
Highest Common Factor (HCF)
Greatest Common Denominator (GCD)
The GCF can be a bit complicated to work out by hand but you can use our handy GCF calculator to figure it out.
In the case of 180 and 100, the greatest common divisor is 20. This means that to simplify the fraction we can divide by the numerator and the denominator by 20 and we get:
180/20
100/20
=
9
5
And there you have it! In just a few short steps we have figured out what 1.80 is as a fraction. The complete answer for your enjoyment is below:
1 4/5
Note: because 180 is greater than 100 we have simplified this fraction even further to a mixed fraction.
Step-by-step explanation:
Find the value of each variable and show work step by step please. Thank you I appreciate it! Also Ramadan Mubarak to anyone who is Muslim seeing this

Answers
Note that the angles above are marked to be similar hence, one half of the base has a length of 16 units.
What is the explanation for the above response?
To solve this problem, we can use the fact that the line bisecting the angle at the top of a triangle also bisects the base. This means that the two halves of the base are equal in length.
Let's call the length of one half of the base "z". Then, the length of the other half of the base is also "z". The total length of the base is 32 units, so we can set up an equation:
z + z = 32
Simplifying this equation, we get:
2z = 32
Dividing both sides by 2, we get:
z = 16
So one half of the base has a length of 16 units.
Learn more about angles at:
https://brainly.com/question/28451077
#SPJ1