Answers
Total Shape: Perimeter is 62 ft. and Area is 110 ft²
What is the area and perimeter ?Area and perimeter are both measurements used in geometry to describe the size and shape of two-dimensional objects such as polygons, circles, and rectangles.
There are consider two rectangular shape 1 and shape 2;
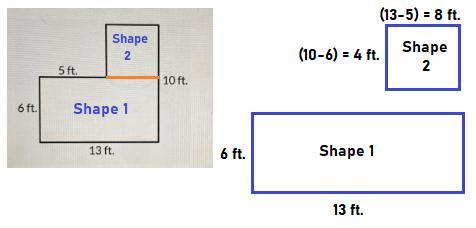
for Shape 1: A small rectangle upper side of figure 2 shown below.
Perimeter = 2 × (6+13) = 38 ft.
Area = 6 × 13 = 78 ft²
for Shape 2: A big rectangle below side of figure 2 shown below.
Perimeter = 2 × (8+4) = 24 ft.
Area = 8 × 4 = 32 ft²
Total Shape:
Perimeter = (38 + 24) ft. = 62 ft.
Area = 78 + 32 = 110 ft²
To know more about rectangle, visit:
https://brainly.com/question/2607596
#SPJ9
Related Questions
Pie chart values
20%. Rice
15%. Others
Pulses. 30%
maize 20%
wheat 15%
Percentage distribution of products in exports of the
given countries.
(a) What is the value (in $ billion) of pulses export
by US? on a billion
(6)
What is the ratio of wheat export of UK to
maize export of IND? 4:10
(e) By what percentage is the maize export of
JAP more than the rice export of AUS?
(d) If the export of AUS is doubled and that of US is
halved but percentage distribution of products of
export remains the same, then find the value of
Export of Rice by US
Export of Pulses by AUS
In USSR, find the ratio of maize export to the
rice export.

Answers
a.) The value of pulses exported by US in billion would be=30 billion.
b.) The ratio of wheat export of UK to maize export of IND would be= 6:5
How to calculate the value of pulses exported?For question a.)
To calculate the pulses, the following steps should be taken as follows:
From the bar chart, the value of pulses in billions = 30 billions.
For question b.)
The ratio of wheat export at UK and maize export at IND would be calculated as follows:
The quantity of wheat export at UK = 24
The quantity of maize export at IND = 20
Therefore, the ratio of wheat to maize = 24:20= 6:5
Learn more about ratio here:
https://brainly.com/question/2328454
#SPJ1
Construction workers are paving a road. The road must drop 4 cm for every 650 cm measured horizontally.
a) What is the slope of the road?
b) Suppose a section of the road drops 24.5 cm. How long is this section of the road measured horizontally?
Answers
Answer:
a)
slope = (-4 cm) / (650 cm)
slope ≈ -0.00615
b) the section of the road measured horizontally is approximately 3983.74 cm long.
Step-by-step explanation:
change in horizontal distance = (change in vertical distance) / slope
change in horizontal distance = (-24.5 cm) / (-0.00615)
change in horizontal distance ≈ 3983.74 cm
Anya graphed the line (y−2)=3(x−1) on the coordinate grid.
A coordinate plane with a line passing through the points, (negative 2, negative 7), (0, negative 1), and (1, 2).
What is the slope of Anya’s line?
Answers
The slope of Anya’s line is equal to 3.
What is the slope-intercept form?Mathematically, the slope-intercept form of the equation of a straight line is given by this mathematical expression;
y = mx + c
Where:
m represents the slope or rate of change.x and y are the points.c represents the y-intercept or initial value.Making y the subject of formula, we have the following:
y - 2 = 3(x - 1)
y = 3x - 3 + 2
y = 3x - 1
Therefore, the slope (m) is equal to 3.
Read more on slope here: brainly.com/question/23086745
#SPJ1
Please help me with math area finding

Answers
Answer:
832.5
Step-by-step explanation:
if you multiply the height by the base and then divide by 2 you will get this answer (it's the formula)
solving separable differential equation DY over DX equals xy+3x-y-3/xy-2x+4y-8
Answers
It looks like the differential equation is
\(\dfrac{dy}{dx} = \dfrac{xy + 3x - y - 3}{xy - 2x + 4y - 8}\)
Factorize the right side by grouping.
\(xy + 3x - y - 3 = x (y + 3) - (y + 3) = (x - 1) (y + 3)\)
\(xy - 2x + 4y - 8 = x (y - 2) + 4 (y - 2) = (x + 4) (y - 2)\)
Now we can separate variables as
\(\dfrac{dy}{dx} = \dfrac{(x-1)(y+3)}{(x+4)(y-2)} \implies \dfrac{y-2}{y+3} \, dy = \dfrac{x-1}{x+4} \, dx\)
Integrate both sides.
\(\displaystyle \int \frac{y-2}{y+3} \, dy = \int \frac{x-1}{x+4} \, dx\)
\(\displaystyle \int \left(1 - \frac5{y+3}\right) \, dy = \int \left(1 - \frac5{x + 4}\right) \, dx\)
\(\implies \boxed{y - 5 \ln|y + 3| = x - 5 \ln|x + 4| + C}\)
You could go on to solve for \(y\) explicitly as a function of \(x\), but that involves a special function called the "product logarithm" or "Lambert W" function, which is probably beyond your scope.
Help with this please.

Answers
Answer:
payment: $179.95total repaid: $43,188interest repaid: $23,188to principal: 46.3%to interest: 53.7%Step-by-step explanation:
You want the monthly payment, total paid, interest paid, and the fractions of the total paid that are principal and interest for a 12-year loan of $20,000 at 9%.
a. Monthly paymentThe loan payment formula applies. P = 20000, APR = 0.09, n = 12, T = 12.
\(\text{pmt}=\dfrac{P\left(\dfrac{\text{APR}}{n}\right)}{\left[1-\left(1+\dfrac{\text{APR}}{n}\right)^{-nT}\right]}\\\\\\\text{pmt}=\dfrac{20000\left(\dfrac{\text{0.09}}{12}\right)}{\left[1-\left(1+\dfrac{\text{0.09}}{12}\right)^{-12\cdot20}\right]}=\dfrac{20000(0.0075)}{1-1.0075^{-240}}\approx 179.95\)
The monthly payment is $179.95.
b. Total paidThe sum of 240 payments of 179.95 is ...
240 · $179.95 = $43,188
The total amount repaid will be $43,188.
c. Interest paidThe amount of interest paid is the difference between the total repaid and the principal amount of the loan:
interest = total - principal
interest = $43,188 -20,000 = $23,188
The amount of interest paid is $23,188.
d. Toward principalThe fraction that goes to the principal is ...
20,000/43,188 × 100% ≈ 46.3%
About 46.3% of the amount repaid goes to principal.
e. Toward interestThe remaining amount goes to interest:
100% -46.3% = 53.7%
About 53.7% of the amount repaid goes to interest.
#95141404393
The net of a triangular prism is shown
below.
8.5 cm
10 cm
10 cm
10 cm
What is the total surface area of the prism?
A 470 cm?
C 390.5 cm?
B 385 cm
D 342.5 cm

Answers
Answer:
i think a.... sorry if im wrong
Step-by-step explanation:
How should I start to complete the equation????

Answers
Answer:
Find the slope and the y-intercept
Step-by-step explanation:
To find slope, use the equation \(\frac{y-y}{x-x}\). First, find two points on the line that are near each other and are whole numbers. Then you substitute the points into the equation. So for example, if I had the points (0,0) and (1,2), the substitution would be:
\(\frac{2-0}{1-0}\)
To find the y-intercept, find where the line crosses over the y-axis. Then put in the y value.
If you do not know where to put slope and y-intercept:
y=mx+b
m=slope
b=y-intercept
slope= output/input
Answer:
the answer may vary, seeing as you could use any of the coordinates, but in my case i got : y = -1/2 + 4
Step-by-step explanation:
formula : y = mx + b
to find your ' b ' you had to determine where the y intersects. in this case, it intersected on positive four.
to determine your m, you have to subtract two of the plotted coordinates from each other, in my case it was (-2,5) and (4,2)
y2 - y1
-----------
x2 - x1
2 - 5
--------
4 - ( -2 )
-3
-----
6
WHICH MEANS
m = -1/2
Interest rate fixed at 6%, n = 26 payments per year, for payment
amounts of $50, $100, $150, $200 (4 separate sheets-1 for each payment amount)
Answers
Answer:
hi the anser might be 600$
Step-by-step explanation:
equivalent equation for 3:7
Answers
Answer:
Hay fracciones infinitas equivalentes a 3
7
. Vea algunos ejemplos:
3
7
, 6
14
, 9
21
, 12
28
, 15
35
, 18
42
, 21
49
, 24
56
, 27
63
, 30
70
, 33
77
, 36
84
, 39
91
, 42
98
, 45
105
, 48
112
, 51
119
, 54
126
, 57
133
, 60
140
...
Lista más fácil de copiar y pegar:
3/7, 6/14, 9/21, 12/28, 15/35, 18/42, 21/49, 24/56, 27/63, 30/70, 33/77, 36/84, 39/91, 42/98, 45/105, 48/112, 51/119, 54/126, 57/133, 60/140 ...
Step-by-step explanation:
Answer: Hello, There! your Answer is Below
6:14
Step-by-step explanation:
Equivalent equations are algebraic equations that have identical solutions or roots. Adding or subtracting the same number or expression to both sides of an equation produces an equivalent equation. Multiplying or dividing both sides of an equation by the same non-zero number produces an equivalent equation.
Hope this Helps!!
Plz explain your Question Better.
How did the temperature change if: at first it decreased by 10 % and then decreased by 30% ?
Answers
Answer: -37%
Step by Step Sol: 100=x
10% of 100 equals 10
100-10 = 90
30% of 90 equals 27
90-27 = 63
63-100 equals -37
The temperature decreased by 37% if the temperature changed if; at first it decreased by 10%.
What is the percentage?It's the ratio of two integers stated as a fraction of a hundred parts. It is a metric for comparing two sets of data, and it is expressed as a percentage using the percent symbol.
We have:
The temperature change if; at first, it decreased by 10 % and then decreased by 30%
Let x be the initial temperature
= (100 - 10) = 90% (first it decreased by 10%)
= 90% of x
= 0.90x
Then decrease by 30 percent,
= 100 - 30 = 70%
= (0 .90x)× 0.70
= 0.63x
The original percentage left 63%
= 100 - 63 = 37
Thus, the temperature decreased by 37% if the temperature changed if; at first it decreased by 10%.
Learn more about the percentage here:
brainly.com/question/8011401
#SPJ5
Match the later drop-down

Answers
1) The expression 2⁻ˣ⁺³ = 3 is matched with graph B.
2 The expression 3ˣ⁺¹=3 is matched with graph C.
3) The expression 4ˣ = 3 is matched with graph
4 ) The expression 1ˣ/4 = 3 is matched with graph
What is the explanation for the above?1) The graph of the expression 2⁻ˣ⁺³ = 3 represents an exponential function where the y-coordinate is 3 when the base 2 raised to the power of (-x+3).
2) The graph of the expression 3ˣ⁺¹=3represents an exponential function where the y-coordinate is 3 when the base 3 raised to the power of (x+1). This graph is a straight line with a slope of 1.
3) The graph of the equation 4ˣ = 3 represents an exponential function where the base 4 raised to the power of x is equal to 3. This equation has a single solution, which can be determined using logarithms.
4) The graph of the expression 1ˣ/4 = 3 represents an exponential function where the base 1 raised to the power of (x/4) is equal to 3.
Learn more about graph at:
https://brainly.com/question/25799000
#SPJ1

PLEASE HELP PLEASE HELPPP

Answers
Answer:
40
Step-by-step explanation:
The LCM is forty.
PLEASE MARK AS BRAINLIEST!
Answer:
40
Step-by-step explanation:
2/5 = 16/40
1/8 = 5/40
Express 0.176pm in meter giving answer in scientific notation
Answers
Answer:
\( 1.76 \times {10}^{ - 13} \: m\)
Step-by-step explanation:
\( \because \: 1 \: pm = {10}^{ - 12} \: m \\ \therefore \: 0.176 \: pm = 0.176 \times {10}^{ - 12} \: m \\ = 1.76 \times {10}^{ - 13} \: m\)
Which expression is equivalent to 36 + 18
O 3(12 + 6).
O 3(33 + 6)
Submi
O 6(6 + 18)
O 6(6+2)
Answers
5. ______ is the transfer of thermal energy by collisions between particles in matter.
a.Convection b.Radiation. c.Conduction. d.Contact
Answers
Answer:
conduction its the answer
NO LINKS!!! URGENT HELP PLEASE!!!
Solve ΔABC using the Law of Sines
1. A = 29°, C = 63°, c = 24
2. A = 72°, B= 35°, c = 21
Answers
Answer:
1) B = 88°, a = 13.1, b = 26.9
2) C = 73°, a = 20.9, b = 12.6
Step-by-step explanation:
To solve for the remaining sides and angles of the triangle, given two sides and an adjacent angle, use the Law of Sines formula:
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
Question 1Given values:
A = 29°C = 63°c = 24As the interior angles of a triangle sum to 180°:
\(\implies A+B+C=180^{\circ}\)
\(\implies B=180^{\circ}-A-C\)
\(\implies B=180^{\circ}-29^{\circ}-63^{\circ}\)
\(\implies B=88^{\circ}\)
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:
\(\implies \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\(\implies \dfrac{a}{\sin 29^{\circ}}=\dfrac{b}{\sin 88^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
Solve for a:
\(\implies \dfrac{a}{\sin 29^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
\(\implies a=\dfrac{24\sin 29^{\circ}}{\sin 63^{\circ}}\)
\(\implies a=13.0876493...\)
\(\implies a=13.1\)
Solve for b:
\(\implies \dfrac{b}{\sin 88^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
\(\implies b=\dfrac{24\sin 88^{\circ}}{\sin 63^{\circ}}\)
\(\implies b=26.9194211...\)
\(\implies b=26.9\)
\(\hrulefill\)
Question 2Given values:
A = 72°B = 35°c = 21As the interior angles of a triangle sum to 180°:
\(\implies A+B+C=180^{\circ}\)
\(\implies C=180^{\circ}-A-B\)
\(\implies C=180^{\circ}-72^{\circ}-35^{\circ}\)
\(\implies C=73^{\circ}\)
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:
\(\implies \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\(\implies \dfrac{a}{\sin 72^{\circ}}=\dfrac{b}{\sin 35^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
Solve for a:
\(\implies \dfrac{a}{\sin 72^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
\(\implies a=\dfrac{21\sin 72^{\circ}}{\sin 73^{\circ}}\)
\(\implies a=20.8847511...\)
\(\implies a=20.9\)
Solve for b:
\(\implies \dfrac{b}{\sin 35^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
\(\implies b=\dfrac{21\sin 35^{\circ}}{\sin 73^{\circ}}\)
\(\implies b=12.5954671...\)
\(\implies b=12.6\)
The vertices of triangle ABC are A(-3, -2), B(-1, 3), and C(2, -4). What type of triangle is it?
Answers
Answer:
Right isosceles triangle----------------------------
Plot the points and connect.
See attached
As we can see this is a right isosceles triangle.
Prove by finding lengths and slopes:
Side ABSlope m = (3 - (-2))/(-1 - (-3)) = 5/2Distance AB = \(\sqrt{(-1-(-3))^2+(3-(-2))^2} =\sqrt{2^2+5^2} =\sqrt{29}\)Side ACSlope m = (-4 - (-2))/(2-(-3)) = -2/5Distance AC = \(\sqrt{(2-(-3))^2+(-4-(-2))^2} =\sqrt{5^2+(-2)^2} =\sqrt{29}\)Proved, as the slopes are negative reciprocals and distances are equal.

The triangle formed by the given vertices be acute angle triangle
The given vertices of triangle,
A(-3, -2), B(-1, 3), and C(2, -4)
We know that,
The distance between two points (x₁ , y₁) and (x₂, y₂) is,
⇒ d = √ [(x₂ - x₁)² + (y₂ - y₁)²]
Now calculate the length of each side using the distance formula:
AB = √[(3 - (-2))² + (-1 - (-3))²]
= √(29)
AC = √[(-4 - (-2))² + (2 - (-3))²]
= √(29)
BC = √[(-4 - 3)² + (2 - 1)²]
= √(50)
= 5√2
Now use the Law of Cosines to find the measure of each angle,
cos(A) = (BC² + AB² - AC²) / (2 BC AB)
cos(B) = (AC² + AB² - BC²) / (2 AC AB)
cos(C) = (BC² + AC² - AB²) / (2 BC AC)
Plugging in the values we calculated, we get:
cos(A) = 5√(2) / 58
cos(B) = 1 / √(58)
cos(C) = 5√(2) / 58
Now we can find the measure of each angle using the inverse cosine function:
A = \(cos^{-1}\)(5√(2) / 58) = 70.53 degrees
B = \(cos^{-1}\)(1 / √(58)) = 56.31 degrees
C = \(cos^{-1}\)(5√(2) / 58) = 70.53 degrees
Since all three angles are less than 90 degrees,
Hence, triangle ABC is an acute angle triangle.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
Intelligence Quotient (IQ) scores are often reported to be normally distributed with μ=100.0 and σ=15.0. A random sample of 51 people is taken. Step 1 of 2 : What is the probability of a random person on the street having an IQ score of less than 98? Round your answer to 4 decimal places, if necessary.
Answers
Answer:
0.4470 = 44.70% probability of a random person on the street having an IQ score of less than 98.
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
What is the probability of a random person on the street having an IQ score of less than 98?
This is the pvalue of Z when X = 98. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{98 - 100}{15}\)
\(Z = -0.1333\)
\(Z = -0.1333\) has a pvalue of 0.4470
0.4470 = 44.70% probability of a random person on the street having an IQ score of less than 98.
Please anyone that can help me

Answers
Answer:
\(|\frac{x}{y} |\)
Step-by-step explanation:
Pre-SolvingWe are given the following expression: \(\sqrt\frac{x^3y^5}{xy^7}\), where x > 0 and y > 0.
We want to simplify it.
To do that, we can first simplify what is under the radical, then take the square root of what is left.
Recall that when simplifying exponents, we don't want any negative or non-integer radicals left.
SolvingTo simplify what is under the radical, we can remember the rule where \(\frac{a^n}{a^m} = a^{n-m}\).
So, that means that \(\frac{x^3}{x} = x^2\) and \(\frac{y^5}{y^7} = y^{-2}\) .
Under the radical, we now have:
\(\sqrt{x^2y^{-2}}\)
Now, we take the square root of both exponents to get:
\(|xy^{-1}|\)
The reason why we need the absolute value signs is because we know that x > 0 and y > 0, but when we take the square root of of \(x^2\) and \(y^{-2}\) , the values of x and y can be either positive or negative, so by taking the absolute value, we ensure that the value is positive.
However, we aren't done yet; remember that we don't want any radicals to be negative, and the integer of y is negative.
Recall that if \(a^{-n}\), that is equal to \(\frac{1}{a^n}\).
So, by using that,
\(|x * \frac{1}{y} |\)
This can be simplified to:
\(|\frac{x}{y} |\)
What is the ratio of frosted cookies to non-frosted cookies?

Answers
Answer:
27:9
Step-by-step explanation:
You purchased a 1.5-liter bottle of olive oil for $11.69. What was the cost per fluid ounce?
Answers
HELP ME PLS!!!
I need help :(

Answers
Answer:
Step-by-step explanation:
Remark
I nearly found the length of a chord PQ. Be careful you don't make the same mistake. It is an arc which is part of the circumference.
Equation
Length of arc PQ = angle/360 * 2* pi * r
Givens
Angle = 110
r = 4 in
Solution
Length of arc PQ = 110/360 * 2 * 3.14 * 4
Length of arc PQ = 0.305555 * 6.28 * 4
Length of arc PQ = 7.67555
Length of arc PQ = 7.68
Help with the following equation 8x²-6x-5=x
Answers
Answer:
\(8 {x}^{2} - 6x - 5 = x\)
\(8 {x}^{2} - 7x - 5 = 0\)
x = (7 + √((-7)^2 - 4(8)(-5)))/(2×8)
= (7 + √(49 + 160))/16
= (7 + √209)/16
= -.4661, 1.3411 (to 4 decimal places)
i need help with this ^

Answers
11 of 3011 of 30 Questions
Question
A baker makes peanut butter cookies and chocolate chip cookies.
She needs 2 cups of flour and 34
cup of butter to make one batch of peanut butter cookies.
She needs 3 cups of flour and 1 cup of butter to make one batch of chocolate chip cookies.
If the baker has 26 cups of flour and 9 cups of butter, how many batches of each type of cookie can she make?
Answers
The baker can only make peanut butter cookies and cannot make any chocolate chip cookies with the given amount of ingredients.
Let's denote the number of batches of peanut butter cookies as "x" and the number of batches of chocolate chip cookies as "y."
From the given information, we can set up the following system of equations:
For the flour:
2x + 3y = 26
For the butter:
34x + y = 9
To solve this system of equations, we can use the substitution method or the elimination method. Let's use the elimination method:
Multiply the first equation by 17 (to make the coefficients of x in both equations the same):
34x + 51y = 442
Now we have the system of equations:
34x + y = 9
34x + 51y = 442
Subtract the first equation from the second equation:
34x + 51y - (34x + y) = 442 - 9
50y = 433
Divide both sides by 50:
y = 433/50
Since the number of batches of cookies cannot be fractional, we need to find a whole number solution for y. However, in this case, y is a fraction, indicating that the given amount of butter is not sufficient to make even one batch of chocolate chip cookies.
for similar questions on ingredients.
https://brainly.com/question/1578467
#SPJ8
Find the equation of the line.
Use exact numbers.

Answers
Take 2 points
(0,4)(-6,0)Slope:-
\(\\ \sf\longmapsto m=\dfrac{0-4}{-6}=\dfrac{4}{6}=\dfrac{2}{3}\)
Equation in point slope form
\(\\ \sf\longmapsto y-y_1=m(x-x_1)\)
\(\\ \sf\longmapsto y-4=\dfrac{2}{3}(x-0)\)
\(\\ \sf\longmapsto 3(y-4)=2x\)
\(\\ \sf\longmapsto 3y-12=2x\)
\(\\ \sf\longmapsto 3y=2x+12\)
\(\\ \sf\longmapsto 2x-3y+12=0\)
A solid is formed by adjoining two hemispheres to the ends of a right circular cylinder. The total volume of the solid is 10 cubic centimeters. Find the radius of the cylinder that produces the minimum surface area. (Round your answer to two decimal places.)
Answers
Answer:
\(r = 1.34\)
Step-by-step explanation:
Given
Solid = Cylinder + 2 hemisphere
\(Volume = 10cm^3\)
Required
Determine the radius (r) that minimizes the surface area
First, we need to determine the volume of the shape.
Volume of Cylinder (V1) is:
\(V_1 = \pi r^2h\)
Volume of 2 hemispheres (V2) is:
\(V_2 = \frac{2}{3}\pi r^3 +\frac{2}{3}\pi r^3\)
\(V_2 = \frac{4}{3}\pi r^3\)
Volume of the solid is:
\(V = V_1 + V_2\)
\(V = \pi r^2h + \frac{4}{3}\pi r^3\)
Substitute 10 for V
\(10 = \pi r^2h + \frac{4}{3}\pi r^3\)
Next, we make h the subject
\(\pi r^2h = 10 - \frac{4}{3}\pi r^3\)
Solve for h
\(h = \frac{10}{\pi r^2} - \frac{\frac{4}{3}\pi r^3 }{\pi r^2}\)
\(h = \frac{10}{\pi r^2} - \frac{4\pi r^3 }{3\pi r^2}\)
\(h = \frac{10}{\pi r^2} - \frac{4r }{3}\)
Next, we determine the surface area
Surface area (A1) of the cylinder:
Note that the cylinder is covered by the 2 hemisphere.
So, we only calculate the surface area of the curved surface.
i.e.
\(A_1 = 2\pi rh\)
Surface Area (A2) of 2 hemispheres is:
\(A_2 = 2\pi r^2+2\pi r^2\)
\(A_2 = 4\pi r^2\)
Surface Area (A) of solid is
\(A = A_1 + A_2\)
\(A = 2\pi rh + 4\pi r^2\)
Substitute \(h = \frac{10}{\pi r^2} - \frac{4r }{3}\)
\(A = 2\pi r(\frac{10}{\pi r^2} - \frac{4r }{3}) + 4\pi r^2\)
Open bracket
\(A = \frac{2\pi r*10}{\pi r^2} - \frac{2\pi r*4r }{3} + 4\pi r^2\)
\(A = \frac{2*10}{r} - \frac{2\pi r*4r }{3} + 4\pi r^2\)
\(A = \frac{20}{r} - \frac{8\pi r^2 }{3} + 4\pi r^2\)
\(A = \frac{20}{r} + \frac{-8\pi r^2 }{3} + 4\pi r^2\)
Take LCM
\(A = \frac{20}{r} + \frac{-8\pi r^2 + 12\pi r^2}{3}\)
\(A = \frac{20}{r} + \frac{4\pi r^2}{3}\)
Differentiate w.r.t r
\(A' = -\frac{20}{r^2} + \frac{8\pi r}{3}\)
Equate A' to 0
\(-\frac{20}{r^2} + \frac{8\pi r}{3} = 0\)
Solve for r
\(\frac{8\pi r}{3} = \frac{20}{r^2}\)
Cross Multiply
\(8\pi r * r^2 = 20 * 3\)
\(8\pi r^3 = 60\)
Divide both sides by \(8\pi\)
\(r^3 = \frac{60}{8\pi}\)
\(r^3 = \frac{15}{2\pi}\)
Take \(\pi = 22/7\)
\(r^3 = \frac{15}{2 * 22/7}\)
\(r^3 = \frac{15}{44/7}\)
\(r^3 = \frac{15*7}{44}\)
\(r^3 = \frac{105}{44}\)
Take cube roots of both sides
\(r = \sqrt[3]{\frac{105}{44}}\)
\(r = \sqrt[3]{2.38636363636}\)
\(r = 1.33632535155\)
\(r = 1.34\) (approximated)
Hence, the radius is 1.34cm
The radius of the cylinder that produces the minimum surface area is 1.34cm and this can be determined by using the formula area and volume of cylinder and hemisphere.
Given :
A solid is formed by adjoining two hemispheres to the ends of a right circular cylinder. The total volume of the solid is 10 cubic centimeters.The volume of a cylinder is given by:
\(\rm V = \pi r^2 h\)
The total volume of the two hemispheres is given by:
\(\rm V' = 2\times \dfrac{2}{3}\pi r^3\)
\(\rm V' = \dfrac{4}{3}\pi r^3\)
Now, the total volume of the solid is given by:
\(\rm V_T = \pi r^2 h+\dfrac{4}{3}\pi r^3\)
Now, substitute the value of the total volume in the above expression and then solve for h.
\(\rm 10 = \pi r^2 h+\dfrac{4}{3}\pi r^3\)
\(\rm h = \dfrac{10}{\pi r^2}-\dfrac{4r}{3}\)
Now, the surface area of the curved surface is given by:
\(\rm A = 2\pi r h\)
Now, the surface area of the two hemispheres is given by:
\(\rm A'=2\times (2\pi r^2)\)
\(\rm A'=4\pi r^2\)
Now, the total area is given by:
\(\rm A_T = 2\pi rh+4\pi r^2\)
Now, substitute the value of 'h' in the above expression.
\(\rm A_T = 2\pi r\left(\dfrac{10}{\pi r^2}-\dfrac{4r}{3}\right)+4\pi r^2\)
Simplify the above expression.
\(\rm A_T = \dfrac{20}{r} + \dfrac{4\pi r^2}{3}\)
Now, differentiate the total area with respect to 'r'.
\(\rm \dfrac{dA_T}{dr} = -\dfrac{20}{r^2} + \dfrac{8\pi r}{3}\)
Now, equate the above expression to zero.
\(\rm 0= -\dfrac{20}{r^2} + \dfrac{8\pi r}{3}\)
Simplify the above expression in order to determine the value of 'r'.
\(8\pi r^3=60\)
r = 1.34 cm
For more information, refer to the link given below:
https://brainly.com/question/11952845
Consider this function.
f(x) = |x – 4| + 6
If the domain is restricted to the portion of the graph with a positive slope, how are the domain and range of the function and its inverse related?
Answers
If we restrict the domain of the function to the portion of the graph with a positive slope, the domain of the inverse function will be the range of the original function for values of x greater than 4, and its range will be all real numbers greater than or equal to 4.
The given function f(x) = |x – 4| + 6 is a piecewise function that contains an absolute value. The absolute value function has a V-shaped graph, and the slope of the graph changes at the point where the absolute value function changes sign. In this case, that point is x=4.
If we restrict the domain of f(x) to the portion of the graph with a positive slope, we are essentially considering the piece of the graph to the right of x=4. This means that x is greater than 4, or x>4.
The domain of the inverse function, f⁻¹(x), will be the range of the original function f(x) for values of x greater than 4. This is because the inverse function reflects the original function over the line y=x. So, if we restrict the domain of f(x) to values greater than 4, the reflected section of the graph will be the range of f⁻¹(x).
The range of f(x) is all real numbers greater than or equal to 6 because the absolute value function always produces a positive or zero value and when x is greater than or equal to 4, we add 6 to that value. The range of f⁻¹(x) will be all real numbers greater than or equal to 4, as this is the domain of the reflected section of the graph.
for more such questions on domain
https://brainly.com/question/2264373
#SPJ8
Help with my math please

Answers
Answer:
$27,000 at 8%$3,000 at 7%Step-by-step explanation:
You want the amounts invested in each of two accounts, one earning 7% and the other earning 8% simple interest, when the total investment of $30,000 earns total interest of $2370.
SetupLet x represent the amount invested at 8%. Then the amount invested at 7% is 30000-x. The total interest earned is ...
0.08(x) +0.07(30000-x) = 2370
Solution0.01x +2100 = 2370 . . . . simplify
0.01x = 270 . . . . . . . . subtract 2100
x = 27000 . . . . . . . multiply by 100
30000-x = 3000
Deshaun invested $27,000 at 8% and $3,000 at 7%.
