what is 7 x + 7 = 2 x - 8
Answers
X= -3
Related Questions
Gold has a density of 19. 3 g/cm^3 and can be rolled into very thin sheets. If a 285 mg sample of gold is rolled into a "circle" of radius 0. 78 cm. Find the thickness of the "circle," in microns.
Answers
The thickness of the given circle made of the sample gold is 77.4 microns.
We know, the density of a material is the ratio of the mass of the material to the volume of the material.
Density = mass/volume
Therefore, volume = mass/density
Here, the density of the gold = 19.3 gm/cm³
Mass of the gold is = 285 mg = 0.285 gm
Therefore, the volume of the given gold is
= mass/density
= 0.285/19.3 cm³
= 0.0148 cm³
The circular sheet of gold has a radius of 0.78 cm.
Therefore, the area of the circular sheet is
= πr² cm²
= π(0.78)² cm²
= 1.911 cm²
Therefore, the thickness of the circular sheet is
= volume of the sheet/ area of the sheet
= 0.0148 cm³/ 1.911 cm²
= 7.74 × 10⁻³ cm
= 7.74 × 10⁻⁵ m
= 77.4 × 10⁻⁶ m
= 77.4 microns
Learn more about the volume of a material here: https://brainly.com/question/9214759
#SPJ4
more than two and fewer than twenty students paid a group price of $391 for concert tickets. if each ticket costs the same whole number of dollars, how many students were in the group?
Answers
There were 17 students in the group, and each student paid the same whole number of dollars for the concert tickets.
To determine the number of students in the group, we need to find a whole number that is greater than 2 and less than 20, and when multiplied by another whole number, results in a product of $391.
First, let's list some factors of 391:
1 x 391 = 391
17 x 23 = 391
Since we are looking for a number of students, we can eliminate the factorization of 1 x 391 because that would mean there is only one student in the group, which contradicts the condition in the question.
Now, let's consider the factorization of 17 x 23. In this case, the number of students in the group would be the smaller factor, which is 17. Therefore, there were 17 students in the group.
To summarize, there were 17 students in the group, and each student paid the same whole number of dollars for the concert tickets.
To know more about students visit:
brainly.com/question/28860774
#SPJ11
(1 point) let a and k be positive constants. which of the given functions is a solution to dydt=k(ay−1)?
Answers
The function y(t) = (a/k) * e^(kt) is the solution to the given differential equation dy/dt = k(a*y - 1).
The given differential equation is dy/dt = k(a*y - 1). To find which of the given functions is a solution, we need to substitute each function into the differential equation and check if the equation holds true.
Let's consider the given functions:
a) y(t) = a^2 * e^(kt) - This function is not a solution to the differential equation because when we substitute it into the equation, we don't get a valid equality. The left side becomes dy/dt = a^2 * k * e^(kt), while the right side becomes k(a * (a^2 * e^(kt)) - 1). These two expressions are not equal, so this function is not a solution.
b) y(t) = (a/k) * e^(kt) - This function is a solution to the differential equation. When we substitute it into the equation, the left side becomes dy/dt = k * (a/k) * e^(kt) = a * e^(kt), and the right side becomes
k * (a * ((a/k) * e^(kt)) - 1) = a * e^(kt). Since the left side and the right side are equal, this function satisfies the differential equation and is a solution.
Therefore, the function y(t) = (a/k) * e^(kt) is the solution to the given differential equation dy/dt = k(a*y - 1).
Learn more about diferential equation here:-brainly.com/question/16245724
#SPJ11
The surface area of a regular square pyramid is 48cm². If the slant height is equal to the base-edge length, find the area of the base.
Answers
What is a ratio that is equivalent to 12:35?
Answers
Answer:
0.3429 is a decimal and 34.29/100 or 34.29% is the percentage for 12/35.
Answer:
24 : 70
Step-by-step explanation:
12 : 35
Multiply each side by 2
12*2 : 35*2
24 : 70
a region is bounded by two concentric circles, as shown by the shaded region in the figure above. the radius of the outer circle, rr, is increasing at a constant rate of 22 inches per second. the radius of the inner circle, rr, is decreasing at a constant rate of 11 inch per second. what is the rate of change, in square inches per second, of the area of the region at the instant when rr is 44 inches and rr is 33 inches?
Answers
The rate of change, in square inches per second, of the area of the region at the instant when R is 44 inches and r is 33 inches is
8363 square inches
How to find the rate of changeThe rate of change is the derivative, the rate of change is calculated by differentiation the area
formula for area of concentric circle is given by
Area A = π(R^2 - r^2) =
R = radius of the inner circle
r = radius of the outer circle
δA/δt = δA/δRδr * δRδr/δt
δA/δt = π * (2RδR/δt - 2rδr/δt)
δA/δt = π * 2(R * δR/δt - r * δr/δt)
where R = 44 and δR/δt = 22
r = 33 and δr/δt = -11
= 2π(44 * 22 - 33 * -11)
= 2π (968 - -363)
= 2π (1331)
= 2662π
= 8362.9196 square inches
Learn more about rate of change here:
https://brainly.com/question/8728504
#SPJ1
in how many ways can 9 yellow marbles be divided among 4 distinguishable cups?
Answers
The number of ways 9 yellow marbles can be divided among 4 distinguishable cups is 126.
Dividing 9 marbles among 4 cups is a combination problem. The number of combinations is given by the formula C(n + r - 1, r - 1), where n is the number of items (marbles) and r is the number of groups (cups). In this case, n = 9 and r = 4. Plugging these values into the formula, we get:
C(9 + 4 - 1, 4 - 1) = C(12, 3) = (12 * 11 * 10) / (3 * 2 * 1) = 220
This means that there are 220 ways to divide 9 yellow marbles into 4 distinguishable cups. However, since the cups are distinguishable, each combination is counted multiple times, once for each permutation of the cups. The number of permutations of n items taken r at a time is given by the formula n! / (n - r)!. In this case, the number of permutations is 4! = 4 * 3 * 2 * 1 = 24.
So, the total number of ways to divide 9 yellow marbles into 4 distinguishable cups is 220 / 24 = 9. This means that there are 126 distinct ways to divide 9 yellow marbles among 4 distinguishable cups.
To learn more about marbles, visit:
https://brainly.com/question/23004973#
#SPJ11
What is the radius of a circle whose equation is y2 y2 8x 6y 21 0?
Answers
The radius of a circle having the equation x² + y² + 8x - 6y + 21 = 0 is 2 units .
In the question ,
it is given that ,
the circle is having the equation ⇒ x² + y² + 8x - 6y + 21 = 0 ,
we know that ,
general equation of circle is written as x² + y² + 2fx + 2gy + c = 0 ;
so , radius of circle is calculated using the below formula ,
radius = √(f² + g² - c)
On comparing, given equation of circle with general equation of circle ,
we get , the values of f = 4 and g = -3 .
So after substituting the values of f , g and c in the radius formula ,
we get ,
radius = √(16 \(+\) 9 - 21)
= √(16 \(+\) 9 - 21)
= √(25 - 21) = √4 = 2 .
Therefore , the given circle has radius = 2 units .
The given question is incomplete , the complete question is
What is the radius of a circle whose equation is x² + y² + 8x - 6y + 21 = 0 ?
Learn more about Circle here
https://brainly.com/question/5720980
#SPJ4
WILL BE GIVEN BRAINLIEST IF ANSWERED
What is your preferred method for solving quadratic equations? Describe the method in your own words and explain why you prefer it over the other methods.
What are the limitations of your preferred method?
Please follow these guidelines for your discussion posts:
Write at least 150–300 words.
Make sure your posts are grammatically and mechanically correct.
Address all parts of the prompt.
Provide at least one example to support your response. (Example choices include an anecdote, statistic, and/or textual evidence.)
Respond to two classmates’ posts with a thoughtful response that goes beyond agreement. Your responses should be at least 40 words and directly address something your peers said in their posts.
Answers
Answer:
Quadratic formula – is the method that is used most often for solving a quadratic equation. If you are using factoring or the quadratic formula, make sure that the equation is in standard form.
There are three basic methods for solving quadratic equations: factoring, using the quadratic formula, and completing the square.
Step-by-step explanation:
suppose that you watch the game show over many years and find that door 1 hides the car 50% of the time, door 2 has the car 40% of the time, and door 3 has the car 10% of the time. what then is your optimal strategy? in other words, which door should you pick initially, and then should you stay or switch? what is your probability of winning with the optimal strategy? explain.
Answers
The optimal strategy is to pick door 1 and stay - this will give you a 50 percentage chance of winning the car.
The optimal strategy to win the game show is to pick door 1 initially and stay. This is because door 1 has the car 50% of the time, which is the highest chance of any of the three doors. If you switch to a different door, then you would have a 40% chance of winning if you switched to door 2, and a 10% chance of winning if you switched to door 3. Since door 1 has the highest chance of having the car, it is the optimal choice to initially select door 1 and stay. By doing so, you have a 50% chance of winning the car.
Learn more about percentage here
https://brainly.com/question/16797504
#SPJ4
June was given 5/7 of the fruit basket .what fraction of the fruit basket is left?
Answers
Answer:
\(\frac{2}{7}\)
Step-by-step explanation:
Another name for 1 is \(\frac{7}{7}\)
\(\frac{7}{7}\) - \(\frac{5}{7}\) = \(\frac{2}{7}\)
The diagram shows a circle with centre O.
A, B & C lie on the circumference of this circle.
Given that AC is a diameter of the circle and ∠BCA = 5 × ∠BAC, find the size of ∠BCA as highlighted in the diagram.

Answers
Answer:
∠ BCA = 75°
Step-by-step explanation:
∠ ABC = 90° ( angle in a semicircle )
then the 2 remaining angles in Δ ABC = 90° , that is
∠ BAC + ∠ BCA = 90° ( ∠ BCA = 5 × ∠ BAC )
∠ BAC + 5 ∠ BAC = 90°
6 ∠ BAC = 90° ( divide both sides by 6 )
∠ BAC = 15°
Then
∠ BCA = 90° - 15° = 75°
what is an obtuse triangle
Answers
Answer:An obtuse-angled triangle is a triangle in which one of the interior angles measures more than 90° degrees. In an obtuse triangle, if one angle measures more than 90°, then the sum of the remaining two angles is less than 90°.
Step-by-step explanation:basically its more than 90 degrees
Answer:
An obtuse triangle is a triangle where one of the interior angles measures more than 90°
Find the coordinates of the vertices of the figure after the given transformation: T<0,7>

Answers
Answer:
Option A.
Step-by-step explanation:
The general transformation works as follows:
T<a,b>(x, y) = (x + a, y + b)
Then for our transformation, we will have:
T<0,7>(x, y) = (x, y + 7)
So now that we know how the transformation works, we need to apply it to the vertices.
Looking at the graph we can see that the vertices are:
X = (-4, -5)
W = (-3, -3)
L = (-5, -2)
Then the new points will be:
X' = (-4, - 5 + 7) = (-4, 2)
W' = (-3, -3 + 7) = (-3, 4)
L' = (-5, -2 + 7) = (-5, 5)
Then the correct option is A.
what is the probability that a randomly selected registered voter who is a republican believes that global warming is a serious issue?
Answers
The probability that a randomly selected registered voter who is a Republican believes that global warming is a serious issue is 0.44 or 44%.
Let A be the event that the selected voter is a Republican, and B be the event that the selected voter believes that global warming is a serious issue.
We need to find P(B|A), the conditional probability of B given A.
Using the information given in the table, we can fill in the following probabilities:
P(A) = 500/1200 = 5/12 (since there are 500 registered voters who are Republicans out of a total of 1200 registered voters)
P(B) = 790/1200 = 79/120 (since there are 790 registered voters who believe that global warming is a serious issue out of a total of 1200 registered voters)
P(A and B) = 220/1200 (since there are 220 registered voters who are Republicans and believe that global warming is a serious issue out of a total of 1200 registered voters)
Then, we can use the formula for conditional probability:
P(B|A) = P(A and B) / P(A)
P(B|A) = (220/1200) / (5/12)
P(B|A) = 0.44
Therefore, the probability is 0.44 or 44%.
To know more about Probabbility:
https://brainly.com/question/11234923
#SPJ4
_____The given question is incomplete, the complete question is given below:
what is the probability that a randomly selected registered voter who is a republican believes that global warming is a serious issue?
Opinions on Global Warming Nonissue Serious Concern Total Democratic 50 450 500 Political Party Republican 280 220 500 Independent 80 120 200 Total 410 790 1200
The graph of f(x) and (x) are shown below. For what interval is the value of (f-g) (x)
Answers
The interval the value of the function (f - g)(x) is negative is (-∞, 2]
What is a function?A function is a rule or definition that maps an input variable unto an output such that each input has exactly one output.
The equations on the possible graphs in the question, obtained from a similar question posted online are;
f(x) = x - 3
g(x) = -0.5·x
(f - g)(x) = x - 3 - (-0.5·x) = 1.5·x - 3
(f - g)(x) = 1.5·x - 3
Therefore; The x-intercept of the function (f - g)(x) = 1.5·x - 3 is; (f - g)(x) = 0 1.5·x - 3
1.5·x - 3 = 0
1.5·x = 3
x = 3/1.5 = 2
x = 2
The y-intercept is the point where, x = 0, therefore;
(f - g)(0) = 1.5×0 - 3 = -3
The interval the function is negative is therefore;
-∞ < x ≤ 2, which is (-∞, 2]The equations of the possible graphs of the function, obtained from a question posted online are;
f(x) = x - 3, g(x) = -0.5·x
The interval the function (f - g)(x) is negative is required
Learn more on the x- and y-intercept of a function here: https://brainly.com/question/29001994
#SPJ1
The slope (m) and the y-intercept (b) of the line 2x + 3y = 12 is:
Answers
Step-by-step explanation:
\(2x + 3y = 12 \\ 3y = - 2x + 12 \\ y = - \frac{2}{3} x + 4\)
slope is -2/3
y intercept is 4
Answer:
The slope is -2/3 and the y intercept is 4
Step-by-step explanation:
2x + 3y = 12
Slope intercept form of a line is
y = mx+b where m is the slope and b is the y intercept
2x + 3y = 12
Subtract 2x from each side
2x-2x+3y = -2x+12
3y = -2x+12
Divide by 3
3y/3 = -2x/3 +12/3
y = -2/3 x +4
The slope is -2/3 and the y intercept is 4
I have multiple questions:
1: 2/3÷4/5
2: 2 1/9÷2/3
3: 3/5÷1 1/4
Answers
Answer:
1: 5/6
2: 3 1/6
3: 12/25
hope this helps!!
p.s
comment if wrong
I 3. A 6-m ladder is leaning against a vertical wall such that the angle between the ground and the ladder is 3. What is the exact height that the ladder reaches up the wall? ✓✓
Answers
The ladder reaches approximately 0.314 meters up the wall.
To find the exact height that the ladder reaches up the wall, we can use trigonometry.
Given:
The ladder has a length of 6 meters.
The angle between the ground and the ladder is 3 degrees.
Let's denote the height the ladder reaches up the wall as h.
In a right triangle formed by the ladder, the height h, and the base of the triangle (the distance from the wall to the ladder's base), we have the following:
sin(theta) = opposite/hypotenuse
sin(3) = h/6
To find h, we can rearrange the equation:
h = sin(3) * 6
Using a calculator, we can evaluate sin(3) to be approximately 0.05234.
Therefore, the height that the ladder reaches up the wall is:
h = 0.05234 * 6
h ≈ 0.314 meters
So, the ladder reaches approximately 0.314 meters up the wall.
Learn more about ladder from
https://brainly.com/question/29316136
#SPJ11
function or not a function?

Answers
Answer:
function
Step-by-step explanation:
no repeated domain means its a function
According to the graph, is f even, odd, or neither(pic provided)?
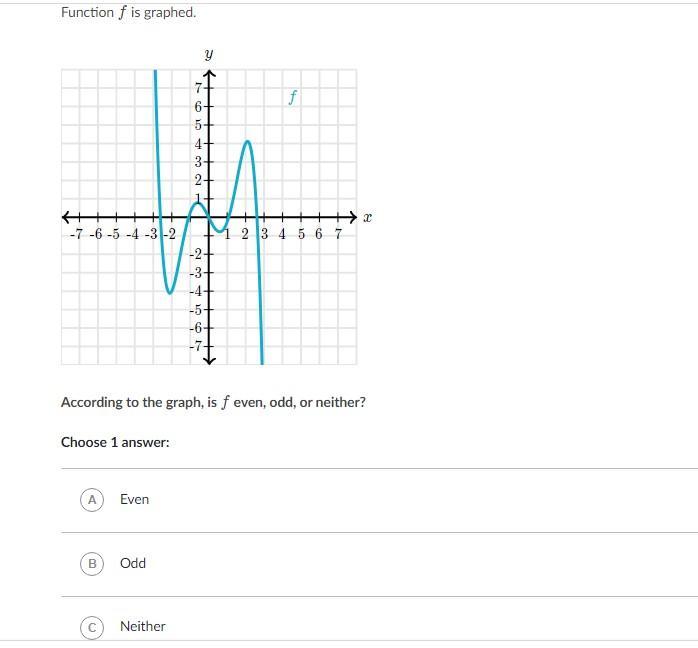
Answers
Answer:
Hello,
Step-by-step explanation:
Since for all real x, f(x)=-f(x),
the function is odd.
Factor completely. 7 +14 x + 7 x^2
Answers
Answer:
(7x+7 )(x+1 )
Step-by-step explanation:
7x²+14x+7
(7x+7 )(x+1 )
7x²+7x+7x+7
7x²+14x+7
Answer: 7(1+x)^2
Step-by-step explanation: I got it wrong because of that person at the top your welcome
The answersssssssssss

Answers
Answer:
pic 1 goes first second pic second slot
Step-by-step explanation:
(1 1/6 − 7/18 )÷2.8/0.5+ 1/18 =
Answers
What is an equation of the line that passes through the point (−1,6) and is parallel to the line 2x+y=9
Answers
Answer:
2x + y = 4
Step-by-step explanation:
2x + y = 9 => y = -2x + 9
Parallel lines have the same slope so m = -2
Given (-1,6)
y = mx + b
6 = -2(-1) + b
6 = 2 + b
b = 4
so y = -2x + 4 or 2x + y = 4
Mary has a spool of ribbon to make bows. She uses 3 8 yard of the spool's ribbon to make a bow. She has 1 4 yard of the ribbon left on the spool. Which choice is the MOST reasonable tor the yards on the spool before Mary made the bows?
A) 3 8 yard
B) 1 2 yard
C) 5 8 yard
D) 5 6 yard
Answers
Answer:
5/8 yards
Step-by-step explanation:
Amount Used: 3/8 yard
Amount Remaining : 1/4
Amount started with = Amount Used + Amount Remaining
We need to find the common denominator for 8 and 4.
3/8 stays 3/8, and 1/4 becomes 2/8 (multiply the numerator and
denominator of 1/4 by 2)
3/8 + 2/8 = 5/8
-Chetan K
Answer:
b) 5/8 yard
Step-by-step explanation:
3/8 of the spool is used to make a bow.
She has 1/4 left. 1/4 = 2/8.
2/8 + 3/8 = 5/8
The population is the 300 students in the fifth and sixth grades. What is an appropriate sample size for the population? A. 10 B. 45 C. 170 D. 300
Answers
The appropriate sample size for the population is 170.
Given that,
The students are conducting a survey about which teacher the students admire the most.
The population is the 300 students in the fifth and sixth grades.
We have to find the appropriate sample size for the population.
Here, it is conducting a survey.
Let confidence level be 95% and the margin of error be 5%.
Then sample size = 169 using the theorem.
So here sample size close to 169 is 170.
Hence the sample size is 170.
Learn more about Sample Size here :
https://brainly.com/question/30100088
#SPJ1
The complete question is,
The students are conducting a survey about which teacher the students admire the most. The population is the 300 students in the fifth and sixth grades. What is an appropriate sample size for the population?
A. 10 B. 45 C. 170 D. 300
what is the lowest value of the rangee of the function shown on the graph? -♾️, -2, 0, 3
Answers
The correct option is -2. The range of function is found to be minimum is -2.
Explain the term minima of the function?The highest and smallest values of a function, respectively, can either be found inside a specific range or across the entire domain. They are sometimes referred to as the function's extrema. The plural forms of a function's maximum and minimum are called maxima and minima, respectively. Let's first examine the function's local maximum and minimal values before delving further into maxima and minima.A function's global minimum is its lowest value across the entire function's range, whereas a localized minimum is its lowest value within a specific local area.
From the given graph of the function:
To get the lowest point of the range of the function, check the value where graph is turning.
This, shows the minima of the function which is -2 at x = 3.
To know more about the minima, here
https://brainly.com/question/9180672
#SPJ1
The complete question is attached-

Explain why the function is differentiable at the given point.f(x, y) = 6 + x ln(xy − 7), (4, 2)The partial derivatives are fx(x, y) =and fy(x, y) =so fx(4, 2) =and fy(4, 2) =Both fx and fy are continuous functions for xy > ???and f is differentiable at (4, 2).Find the linearization L(x, y) of f(x, y) at (4, 2). L(x, y) =
Answers
The function f(x,y) = 6 + x ln(xy-7) is differentiable at the point (4,2).
We can find the partial derivative fx(x,y) by applying the chain rule of differentiation to the function f(x,y) = 6 + x ln(xy-7), as follows:
fx(x,y) = ln(xy-7) + x(1/(xy-7))(ydx/dx)
= ln(xy-7) + 1/(y-7)*x
where dx/dx = 1 is the derivative of x with respect to itself. Similarly, the partial derivative fy(x,y) can be obtained as:
fy(x,y) = x(1/(xy-7))(xdy/dy)
= x/(xy-7)
where dy/dy = 1 is the derivative of y with respect to itself.
To show that fx and fy are continuous at the point (4,2), we need to evaluate them at that point and show that the resulting values are finite. Substituting x = 4 and y = 2 into the equations for fx and fy, we get:
fx(4,2) = ln(1) + 1/(2-7)4 = -4/5
fy(4,2) = 4/(42-7) = -4/3
Since both fx(4,2) and fy(4,2) are finite, we can conclude that the partial derivatives of f exist and are continuous at (4,2).
To know more about derivative here
https://brainly.com/question/30074964
#SPJ4
Complete Question:
Explain why the function is differentiable at the given point.
f(x, y) = 6 + x ln(xy − 7), (4, 2)
The partial derivatives are fx(x, y) =
and fy(x, y) =
What is the sum of 17.25 and 1.725 , to the nearest integer?
Answers
The sum of 17.25 and 1.725, to the nearest integer, is 19.
First, let's add the two numbers together: 17.25 + 1.725 = 19.975
Next, we need to round the sum to the nearest integer. To do this, we need to look at the tenths place of the number. Since the tenths place is a nine, we need to round up to the nearest integer.
In this case, the nearest integer is 19.
To check our answer, we can add the two numbers together again using a calculator and confirm that the answer is 19.
To make sure we understand how to round to the nearest integer, let's look at another example. If we add 3.45 + 2.735, the sum is 6.185.
Looking at the hundredths place, we see that it is a five. Since five is greater than or equal to five, we need to round up to the nearest integer.
In this case, the nearest integer is 7.
To check our answer, we can add the two numbers together again using a calculator and confirm that the answer is 7.
In summary, to round a number to the nearest integer, we need to look at the tenths place. If the tenths place is greater than or equal to five, we round up to the nearest integer. If it is less than five, we round down to the nearest integer.
Therefore, the sum of 17.25 and 1.725, to the nearest integer, is 19.
To learn more about integer visit:
https://brainly.com/question/929808
#SPJ4
The sum of 17.25 and 1.725 is 18.975. To the nearest integer, this number is rounded up to 19.
Rounding to the nearest integer involves finding the closest whole number to a decimal or fractional number. When the decimal portion of a number is greater than or equal to 0.5, the number is rounded up to the next whole number. When the decimal portion of a number is less than 0.5, the number is rounded down to the previous whole number. In this case, the decimal portion of 18.975 is greater than 0.5, so the number is rounded up to 19.
Learn more about Sum:
https://brainly.com/question/28421287
#SPJ4