What happens to the value of the expression n+15n+15n, plus, 15 as nnn decreases?
Choose 1 answer:
Choose 1 answer:
(Choice A)
A
It increases.
(Choice B)
B
It decreases.
(Choice C)
C
It stays the same.
Answers
Answer:
B: The value will decrease.
Step-by-step explanation:
Answer:
Choice B - it decreases
Step-by-step explanation:
hope this helps
Related Questions
In the past, Peter Kelie's fre dealership in Baton Rouge soid an average of 1,200 radials each year, in the past 2 years, 220 and 260 , respectively were sold in fall, 350 and 310 in winter 150 and 175 in speng. and 320 and 615 in surmer. Whth a major eppansion planned, Kelle projects sales next year to increase to 1,400 radials. Based en next year's projected sales, the demand for each season is going to be (entor your responses as whole numbers):
Answers
Fall: 275 radials
Winter: 325 radials
Spring: 162 radials
Summer: 638 radials
The demand for each season is estimated based on the historical sales data provided and the projected increase in sales for the upcoming year.
To calculate the estimated demand for each season, we take the average of the past two years' sales for each season and then adjust it proportionally to the projected total sales for the next year.
Here's the breakdown of the calculation for each season:
Fall: Taking the average of the past two years' fall sales (220 and 260) gives us \(\frac{220+260}{2}\)= 240. We then adjust this value proportionally to the projected sales for next year: (\(\frac{240}{580}\)) * 1,400 ≈ 575. Rounding this to the nearest whole number, we get an estimated demand of 575 radials for the fall season.
Winter: Following the same process, we find the average of the past two years' winter sales (350 and 310) as \(\frac{350+310}{2}\) = 330. Adjusting this value proportionally to the projected sales for next year: (\(\frac{330}{660}\)) * 1,400 ≈ 700. Rounded to the nearest whole number, the estimated demand for the winter season is 700 radials.
Spring: Calculating the average of the past two years' spring sales (150 and 175) gives us \(\frac{150+175}{2}\) = 162. Adjusting this value proportionally to the projected sales for next year: (\(\frac{162}{325}\)) * 1,400 ≈ 698. Rounded to the nearest whole number, the estimated demand for the spring season is 698 radials.
Summer: Similarly, taking the average of the past two years' summer sales (320 and 615) gives us \(\frac{320+615}{2}\) = 467. Adjusting this value proportionally to the projected sales for next year: (\(\frac{467}{935}\)) * 1,400 ≈ 700. Rounded to the nearest whole number, the estimated demand for the summer season is 700 radials.
Therefore, based on the projected sales of 1,400 radials next year, the estimated demand for each season is approximate: Fall - 575 radials, Winter - 700 radials, Spring - 698 radials, and Summer - 700 radials.
Learn more about demand here: https://brainly.com/question/33667139
#SPJ11
Select the correct answer. Solve the following equation for x. 7 x 2 − 112 = 0 A. x = -4, x = -4 B. x = 4, x = 4 C. x = -4, x = 4 D. x = 5, x = -5
Answers
The correct answer is option C: x = -4, x = 4. Both values of x satisfy the equation 7x^2 - 112 = 0.
To solve the given equation, we need to isolate the variable x. Firstly, we add 112 to both sides of the equation to eliminate the constant term. This gives us the equation 7x^2 = 112.
Next, we divide both sides by 7 to get x^2 = 16. Taking the square root of both sides, we get two possible values of x: x = ±4. It is important to check the solutions obtained by substituting them back into the original equation to ensure they are valid.
In this case, both -4 and 4 make the equation true, so both values are acceptable.
To learn more about : equation
https://brainly.com/question/17145398
#SPJ11
At noon, Trevor and Kim start running from the same point. Trevor runs east at a speed of 8 km/h and Kim runs west at a speed of 6 km/h. At what time will they be 21 km apart?
Answers
Trevor and Kim will be situated 21 kilometers apart from each other at 1:30 PM. They will be separated by a distance of 21 km when the clock strikes 1:30 in the afternoon.
To determine at what time Trevor and Kim will be 21 km apart, we can set up a distance-time equation based on their relative speeds and distances.
Let's assume that t represents the time elapsed in hours since noon. At time t, Trevor would have traveled a distance of 8t km, while Kim would have traveled a distance of 6t km in the opposite direction.
Since they are running in opposite directions, the total distance between them is the sum of the distances they have traveled:
Total distance = 8t + 6t
We want to find the time when this total distance equals 21 km:
8t + 6t = 21
Combining like terms, we have:
14t = 21
To solve for t, we divide both sides of the equation by 14:
t = 21 / 14
Simplifying, we find:
t = 3 / 2
So, they will be 21 km apart after 3/2 hours, which is equivalent to 1 hour and 30 minutes.
Therefore, Trevor and Kim will be 21 km apart at 1:30 PM.
For more such question on distance . visit :
https://brainly.com/question/30395212
#SPJ8
if. david has 19 bills in his wallet worth 125 all fives and tens how many of each bill does he have
Answers
Answer:
T=6 NUMBER OF TEN DOLLAR BILLS.
F=13 NUMBER OF FIVE DOLLAR BILLS.
Step-by-step explanation:
F+T=19 F=19-T
5F+10T=125 NOW SUBSTITUTE (19-T) FOR F IN THIS EQUATION & SOLVE FOR T
5(19-T)+10T=125
95-5T+10T=125
5T=125-95
5T=30
T=30/5
PROOF
5*13+10*6=125
65+60=125
125=125
the row numbers along the left side of a worksheet are as follows: 1 2 4 5 6. this indicates that row 3 is:
Answers
The row numbers along the left side of the worksheet are 1, 2, 4, 5, 6. We can observe that there is a missing number in the sequence, specifically the number 3. Therefore, based on the pattern, we can deduce that row 3 is missing from the worksheet.
Based on the given information, the row numbers along the left side of the worksheet are 1, 2, 4, 5, 6, with a missing number in the sequence, which is the number 3.
The presence of the numbers 1, 2, 4, 5, and 6 indicates that rows corresponding to those numbers exist in the worksheet. However, there is no row with the number 3 mentioned in the sequence. Thus, we can conclude that row 3 is missing from the worksheet.
It is important to note that the missing row could be intentional or accidental, but based on the given information, we can deduce that there is a discontinuity in the row numbering, specifically the absence of row 3.
Learn more about number from
https://brainly.com/question/27894163
#SPJ11
How will you describe the graph of polynomial function if the degree is odd number and the leading coefficient is positive?
Answers
We say cubic polynomial if the degree of polynomial is odd number, and the graph is said cubic polynomial graph.
What is the degree of polynomial function?The equation which has only positive integer exponent are called polynomial function. Such as 6x³+4x²+2x+1=0 where the power 3,2, 1 are the degree of polynomial.
What is cubic polynomial?The polynomial function whose first degree is odd number is called cubic polynomial.
hence, the graph is cubic polynomial.
to learn more about polynomial visit:
https://brainly.com/question/14219138
#SPJ4
Find the length of side AC. Round to the nearest tenth

Answers
Answer:
AC ≈ 4.7 ft.
Step-by-step explanation:
GIVEN :-
Length of AB = 5 ftLength of AC = x ft∠A = 20°TO FIND :-
Value of 'x'FACTS TO KNOW BEFORE SOLVING :-
\(\cos \theta = \frac{Side \: adjacent \: to \: \theta}{Hypotenuse}\)
SOLUTION :-
Side adjacent to ∠A = AC = x
Hypotenuse = AB = 5 ft
⇒ \(\cos 20 = \frac{x}{5}\)
⇒ \(0.9396.... = \frac{x}{5}\)
⇒ \(x = (0.9396...) \times 5 = 4.6984....\) ≈ 4.7 ft
d=rt help solve for r
Answers
Answer:
r=d/t
Step-by-step explanation:
Step 1: Flip the equation.
rt=d
Step 2: Divide both sides by t.
rt/t=d/t
r=d/t
use the ratio test to determine whether the series is convergent or divergent. [infinity] 15n (n 1)52n 1 n = 1
Answers
The limit of the ratio test is greater than 1, the series is divergent by the ratio test. Therefore, we can conclude that the series [infinity] 15n(n+1)^5/(2n+1) is divergent.
To apply the ratio test, we need to compute the limit of the ratio of consecutive terms: lim (n→∞) |(15n(n+1)^5)/(2n+1)|
We can simplify this expression by dividing the numerator and denominator by n^5: lim (n→∞) |(15(n+1)/(n))((n+1)/n)^5/(2/n+1)|. As n goes to infinity, the first factor approaches 15 and the third factor approaches 0. Therefore, we have:lim (n→∞) |15((n+1)/n)^5/(2/n+1)|
To evaluate this limit, we can use L'Hôpital's rule: lim (n→∞) |(5(n+1)/n^2)((n+1)/n)^4/(−2/n^2)|
Simplifying the numerator and denominator, we get: lim (n→∞) |(5(n+1)/(−2))(n+1)/n^6|
The factor of (n+1)/n^6 goes to 0 as n goes to infinity, so we are left with: lim (n→∞) |(5(n+1)/(−2))| = ∞
To know more about convergent or divergent:
https://brainly.com/question/31494394
#SPJ11
To be able to go on a trip to South America, Salma decides to save for 2 years. She opens a savings account with $700 . The account pays simple interest at an annual rate of 5% . She doesn't make any more deposits.
(a) How much total interest will Salma earn?
(b) What will the total amount in the account be (including interest)?
Answers
Answer:
(a) I'm pretty sure it's $71.75
(b) the total would be $771.75 if i calculated it right...
To the nearest foot, what is the height of the fireworks when they explode?

Answers
Answer:
87 feet1. You can find the value of the vertex of the parabola as following: 2. Substitute values: a=-16 b=70 Then: 3. Substitute the value obtained into the equation given in the problem. Therefore, you obtain the following result: 4. To the nearest foot: h=87 feetStep-by-step explanation:
#hopeithelpsstay safe and keep wellmark me as brain liest plsa wire of length 12 inches can be bent into a circle, square, or cut into two pieces and bent into both. how much wire should be used for the circle if the total area enclosed must be
Answers
The total area enclosed for a circle must be 40 inches.
To calculate how much wire should be used for the circle, use the formula for the circumference of a circle, C = 2πr, where r is the radius of the circle.
Plugging in the area (A = πr2), you get C = 2*(A/π)1/2. Thus, the total length of wire needed for the circle is 2*(40/π)1/2, which is approximately 12.8 inches.
To calculate the length of wire needed for the circle, the formula for the circumference of a circle is used. This is because the circumference of the circle is the total length of wire needed to make the shape.
The formula for the circumference of a circle is C = 2πr, where r is the radius of the circle. Since we know the area of the circle, A = πr2, we can plug this into the equation for the circumference to get C = 2*(A/π)1/2.
Plugging in the total area (40 inches) gives us the total length of wire needed, which is approximately 12.8 inches.
To know more about circumference click on below link:
https://brainly.com/question/28757341#
#SPJ11
2/3 feet into inches
Answers
Answer:
12÷3=4
4inches is 2/3 of a foot.
Find values of a and b so that y=a⋅bx and the line y=x+4 are tangent at x=0. Hint: What must be equivalent between the exponential function and the tangent line? a=
b=
Answers
The values of a and b that make the line y = a⋅bx tangent to the line y=x+4 at x = 0 are a = 4 and b = 4
First, let's evaluate the exponential function y = a⋅bx at x = 0:
y = a⋅b(0)
y = a⋅1
y = a
So, the value of y for the exponential function at x = 0 is equal to a.
Now, let's evaluate the line y = x + 4 at x = 0:
y = 0 + 4
y = 4
To have the two lines tangent at x = 0, we need the y-values to be equal. Therefore, we have:
a = 4
Now, let's consider the derivative of y = a⋅bx:
dy/dx = abx-1
To find the value of b, we need to equate the derivative to the slope of the line y = x + 4, which is 1:
abx-1 = 1
Substituting x = 0:
ab0-1 = 1
ab-1 = 1
a/b = 1
Since we know that a = 4, we can substitute this value:
4/b = 1
Solving for b:
b = 4
∴ a = 4 and b = 4.
To know more about tangent to the line refer here:
https://brainly.com/question/12648495#
#SPJ11
Simplify the following rational expression and express in expanded form.
6
m
2
−
5
m
y
−
y
2
12
m
+
2
y
=
12m+2y
6m
2
−5my−
Answers
Answer:
6m²-5my-12m
Step-by-step explanation:
dont get it oooo
Answer:
On khan Academy,
it is m-y/2
✨‼️will mark the brainliest to the one who gives me the answer‼️✨
A boy is flying a kite. The string of the kite has a 40° angle of elevation parallel to the ground. The kite is 30 meters above the ground, and the boy’s hand is 1.5 meters in the air. Find the length of the kite string. Round your answer to the nearest meter.
Answers
Answer:
Step-by-step explanation:
we want to find the Hypotenuse of the triangle being made by the string , the ground and the height off the ground. Also we will have to subtract the small triangle of the boy's hand from the ground
the big triangle Hyp is found by using
SOH or Sin = Opp / Hyp
we know the sin and the Opposite soooo
Sin(40) = 30 / Hyp
Hyp = 30 / Sin(40) [ I'll use my calculator for this ]
Hyp = 46.67 m ( this is the Hypotenuse of the big triangle )
the small one is
Sin(40) = 1.5 / Hyp
Hyp = 1.5 / Sin(40) [calculator again ]
Hyp = 0.9641 m
Now subtract the small one from the big one
46.67 - 0.9641 = 45.7 m
rounding to the nearest meter the answer is 46 m
(4 points) Calculate simplified expressions for the consumption function, investment function, and the net export function.
C=3.25+.75(Y-3)= 1 +.75Y
NX=-1 +.1Y
I=1.3 -.3r
Answers
The simplified expressions represent the level of consumption, investment, and net exports at a particular level of income and interest rates.
The consumption function represents the relationship between the aggregate level of consumption and the total level of income in the economy.
The investment function shows the level of investment planned by businesses at different interest rates. The net export function calculates the difference between exports and imports as a function of income, while the level of imports is positively related to the level of income, and exports are negatively related to the level of income.
Given:C = 3.25 + 0.75(Y - 3)
We can simplify the consumption function as follows:
C = 1 + 0.75YY - 3 = disposable income = Yd
C = 1 + 0.75(Yd)
C = 1 + 0.75Y
For the investment function: I = 1.3 - 0.3r
Where I is investment and r is the interest rate.
For the net export function: NX = -1 + 0.1Y
Thus, the simplified expressions for the consumption function, investment function, and net export function are:
C = 1 + 0.75YI = 1.3 - 0.3rNX = -1 + 0.1Y
The simplified expressions represent the level of consumption, investment, and net exports at a particular level of income and interest rates.
To know more about interest,
https://brainly.com/question/25720319
#SPJ11
one person always say the truth, one person always lies, one person sometimes says the truth or sometimes lies, one question
Answers
If they indicate a different door, they are lying. Based on their response, you can determine which door leads to the treasure.
To determine which person always tells the truth and which person always lies, you can ask any one of them a question whose answer you already know. For example, you could ask "What is my name?" and then verify the answer with someone else. Once you have identified the person who always tells the truth and the person who always lies, you can ask the person who sometimes tells the truth or lies a question that will allow you to determine whether they are telling the truth or lying. A good question to ask the person who sometimes tells the truth or lies is "If I asked one of the other two people which door leads to the treasure, what would they say?" If the person responds by indicating the door that leads to the treasure, they are telling the truth.
Learn more about treasure here
https://brainly.com/question/16028870
#SPJ11
Evaluate a^7 - 4b for a =3 and b= -1
Answers
Answer:
2187+4
= 2191
Step-by-step explanation:
plz brainliest :)
= (3)^7 - (4)(-1)
= 3 * 3 * 3 - (-4)
= 27 - (-4)
= 27 + 4
= 32
Evaluate the integral: S1 0 (-x³ - 2x² - x + 3)dx
Answers
The integral: S1 0 (-x³ - 2x² - x + 3)dx is -1/12
An integral is a mathematical operation that calculates the area under a curve or the value of a function at a specific point. It is denoted by the symbol ∫ and is used in calculus to find the total amount of change over an interval.
To evaluate the integral:
\($ \int_0^1 (-x^3 - 2x^2 - x + 3)dx $\)
We can integrate each term of the polynomial separately using the power rule of integration, which states that:
\($ \int x^n dx = \frac{x^{n+1}}{n+1} + C $\)
where C is the constant of integration.
So, we have:
\($ \int_0^1 (-x^3 - 2x^2 - x + 3)dx = \left[-\frac{x^4}{4} - \frac{2x^3}{3} - \frac{x^2}{2} + 3x\right]_0^1 $\)
Now we can substitute the upper limit of integration (1) into the expression, and then subtract the result of substituting the lower limit of integration (0):
\($ \left[-\frac{1^4}{4} - \frac{2(1^3)}{3} - \frac{1^2}{2} + 3(1)\right] - \left[-\frac{0^4}{4} - \frac{2(0^3)}{3} - \frac{0^2}{2} + 3(0)\right] $\)
Simplifying:
\($ = \left[-\frac{1}{4} - \frac{2}{3} - \frac{1}{2} + 3\right] - \left[0\right] $\)
\($ = -\frac{1}{12} $\)
Therefore,
\($ \int_0^1 (-x^3 - 2x^2 - x + 3)dx = -\frac{1}{12} $\)
To learn more about substituting visit:
https://brainly.com/question/10423146
#SPJ11
What is the fuction rule this table

Answers
The table values using function rule y = -10x - 2 is (8,-2,-12,-52)
Given function
y = -10x - 2
From the table
x = -1 , 0 , 1 , 5
substitute x values in function
if x = -1
y = -10x - 2
= -10(-1) - 2
= 10 - 2
y = 8
if x = 0
y = -10(0) -2
y = -2
if x = 1
y = -10(1) - 2
y = -12
if x = 5
y = -10(5) -2
y = -52
y values (8,-2,-12,-52)
Table:
x y
-1 8
0 -2
1 -12
5 -52
Learn more about the values and function rule here:
https://brainly.com/question/20527725
#SPJ1
Apply the distributive property to factor out the greatest common factor. 6+30=6+30=6, plus, 30, equals
Answers
Step-by-step explanation:
the distributive property is 6(1+5), the greatest common factor is 6
Answer:
6(1+5)
Step-by-step explanation:
khan told me
what is 10x + 5 = 105??
Answers
Answer:
\(x=10\)
Step-by-step explanation:
\(10x+5=105 \\ \\ 10x=100 \\ \\ x=10\)
Answer:
x=10
Step-by-step explanation:
10x+5=105
-5 -5
10x=100
divide by 10
x=10
Another weird looking question. Someone help please

Answers
The measure of the angle m∠CBD between points CD is equal to 495°°
How to evaluate for the angle m∠CBDFrom the question, we observe that the larger angle between AD consists of the two angles between m∠ABC and m∠CBD, so we shall sum the two small angles and equate the result to the larger angle m∠ABD to solve for the value of x as follows:
7x - 9 + 6x + 27 = 96
x + 18 = 96
x = 96 - 18 {collect like terms}
x = 78
put the value of x in m∠CBD;
m∠CBD = 6(78) + 27
m∠CBD = 495
In conclusion, the measure of the angle m∠CBD between points CD is equal to 495°
Read more about angles here:https://brainly.com/question/1475130
#SPJ1
us the data set to choose the two measures that are equivlent 4, 5, 6, 7, 8
Answers
The mean and median of the data are equivalent and the value is 6.
The mean (average) of a data set can be calculated by adding up all the numbers in the collection and dividing by the total number of values in the set.
When a data set is sorted from least to greatest, the median is the middle. The value that pops up most frequently in a data set is its mode.Between the lowest and highest value is the range. You subtract the lowest value from the greatest value to calculate it.The exact midpoint between the lowest and highest values in a set of data is the midway value. Finding the middle requires adding the smallest and greatest values together, then dividing the result by two.Let us find the mean of the data set :
mean = (4 + 5 + 6 + 7 + 8) ÷ 5 = 30÷ 5 = 6
Median = 6 middle value.
Therefore the mean and median are equivalent.
To learn more about mean visit:
https://brainly.com/question/28670966
#SPJ1
Let Pij = the production of product i in period j. To specify that production of product 2 in period 4 and in period 5 differs by no more than 80 units, we need to add which pair of constraints?
P52-P42 <= 80; P42-P52 <= 80
None of the other above.
P24 - P25 <= 80; P25-P24 >= 80
O P24 - P25 >= 80; P25-P24 >= 80
P24 - P25 <= 80; P25-P24 <= 80
Answers
The correct pair of constraints that needs to be added to specify that production of product 2 in period 4 and in period 5 differs by no more than 80 units is: P24 - P25 <= 80; P25-P24 <= 80. Therefore, the correct option is 5.
Here, the given information is Pij = the production of product i in period j. We need to find the pair of constraints that will specify that production of product 2 in period 4 and in period 5 differs by no more than 80 units. Thus, let the production of product 2 in period 4 and in period 5 be represented as P24 and P25 respectively.
Therefore, we can write the following inequalities:
P24 - P25 <= 80
This is because the production of product 2 in period 5 can be at most 80 units less than that of period 4. This inequality represents the difference being less than or equal to 80 units.
P25-P24 <= 80
This is because the production of product 2 in period 5 can be at most 80 units more than that of period 4. This inequality represents the difference being less than or equal to 80 units.
Therefore, we need to add the pair of constraints P24 - P25 <= 80 and P25-P24 <= 80 to specify that production of product 2 in period 4 and in period 5 differs by no more than 80 units. Hence, option 5 is the correct answer.
Learn more about Constraints:
https://brainly.com/question/3469433
#SPJ11
Hello
Can you help me to do these two exercises please I block on those please it is on the derivatives of a number
Thank you so much in advance!!!

Answers
Answer:
First rememeber that if we have a function like:
g(x) = x^n
then:
dg(x)/dx = g'(x) = n*x^(n - 1)
And also if we have:
g(x) = f(x) + h(x)
then:
dg(x)/dx = g'(x) = f'(x) + h'(x)
1) We have the function f(x) = (x + 1)^2
We can rewrite this as:
f(x) = x^2 + 2*x + 1
Using both things written above, we know that:
f'(x) = 2*x + 1*2 = 2*x + 2
And we want to find f'(-2), so we only need to evaluate the above function in x = -2, this is:
f'(-2) = 2*-2 + 2 = -4 + 2 = -2
f'(-2) = -2
b) I suppose that this refers to the inverse function of f(x)
An inverse function is such that:
g( f(x)) = x
f( g(x)) = x
For f(x) = (x + 1)^2
The inverse will be something that first cancels that square, and then subtracts 1.
Then:
g(x) = √x - 1
if we evaluate this in f(x) we get:
g( f(x)) = √(f(x)) - 1 = √(x + 1)^2 - 1 = (x + 1) - 1 = x
Then the inverse function of f(x) is:
g(x) = √x - 1
This can also be written as:
g(x) = x^(1/2) - 1
Then the derivative of this will be:
g'(x) = (1/2)*x^(1/2 - 1) = (1/2)*x^(-1/2) = (1/2)*(1/√x)
given m || n, calculate the value of x
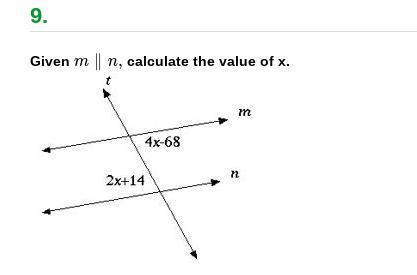
Answers
Answer: x = 41
Step-by-step explanation:
4x - 68 = 2x + 14 [since alternate interior angles are equal]
4x - 2x = 14 + 68
2x = 82
x = 41
Answer:
x=41
Step-by-step explanation:
this problem can be solved using the alternate interior angles converse theorem, which states that if two coplanar lines are cut by a transversal so that a pair of alternate inerior angles are congruent, then the two lines are parallel.
4x-68=2x+14
2x-68=14 <- subtract 2x from both sides
2x=82 <- add 68 to both sides
x=41 <- divide both sides by 2
check:
4(41)-68=96
2(41)+14=96
In this problem we have datapoints (0,2), (1,4.5), (3,7), (5,7), (6,5.2). = We expect these points to lie roughly on a parabola, and we want to find the quadratic equation y(t) Bo + Bit + Bat? which best approximates this data (according to a least squared error minimization). Let's figure out how to do it. y(0) y(1) a) Find a formula for the vector y(3) in terms of Bo, B1, and B2. Hint: Plug in 0, 1, etcetera y(5) y(6) into the formula for y(t). y(0) Bo y(1) b) Let x = Bi Find a 5 x 3 matrix A such that Ax = Hint: The first two columns B2 y(5) y(6) of A should be familiar. One of the entries in A should be 32 = 9. y(3) c) For the rest of this problem, please feel welcome to use computer software, e.g. to find the inverse of a 3 x 3 matrix. Find the normal equation for the minimization of || Ax – 6||, where 2 4.5 b= 7 7 5.2 d) Solve the normal equation, and write down the best-fitting quadratic function.
Answers
For this problem, we have datapoints (0,2), (1,4.5), (3,7), (5,7), (6,5.2). We expect these points to lie roughly on a deviation parabola, and we want to find the quadratic equation y(t) Bo + Bit + Bat
which best approximates this data (according to a least squared error minimization). Let's figure out how to do it.(a)Find a formula for the vector y(3) in terms of Bo, B1, and B2.Hint: Plug in 0, 1, etcetera y(5) y(6) into the formula for y(t).y(0) = Boy(1) = Bo + B1y(3) = Bo + 3B1 + 9B2y(5) = Bo + 5B1 + 25B2y(6) = Bo + 6B1 + 36B2(b)
Let x = [B0, B1, B2]TA = [1, 0, 0; 1, 1, 1; 1, 3, 9; 1, 5, 25; 1, 6, 36]x = [y(0), y(1), y(3), y(5), y(6)]T(c)For the rest of this problem, please feel welcome to use computer software, e.g. to find the inverse of a 3 x 3 matrix. Find the normal equation for the minimization of || Ax – b||, where 2 4.5 b= 7 7 5.2
The normal equation is A^TAx = A^TbA^TA = [5, 15, 55; 15, 55, 205; 55, 205, 781]A^Tb = [25.7, 129.5, 476.7]x = [Bo, B1, B2]T(d)
Solve the normal equation, and write down the best-fitting quadratic function.
A^TAx = A^Tb => x = (A^TA)^-1(A^Tb)x = [1.9241, -0.1153, -0.0175]Tbest-fitting quadratic function:y(t) = 1.9241 - 0.1153t - 0.0175t2
To know more about standard deviation visit:
https://brainly.com/question/23907081
#SPJ11
What is 60% of 20?
PLEASE ANSWER ASAP
Answers
Answer:
the answer would be 12
Step-by-step explanation:
Answer:
12
Step-by-step explanation:
.6 × 20 = 12. Hope this helps!