What figure models 6 divided by 3/2?
(6 divided by 3/2 equals 4)
NEEDS HELP NOW!
BRAINLIEST!

Answers
Pls mark brainliest
Related Questions
help me with this please

Answers
Step-by-step explanation:
the domain is the interval or set of all valid values for the input variable (x).
this is here all real (R) values.
the range is the interval or set of all valid values for the result variable (y).
this is here all integer values.
INT(4.6) = 5
INT(-2.3) = -2
INT(sqrt(2)) = INT(1.414213562...) = 1
suppose you start with a single bacterium of streptococcus at hour 0 , and it has a generation time of 60 minutes. how many bacteria will you have at the end of hour 24
Answers
Answer:
60x24
Step-by-step explanation:
60x24=1224
May I please get some help on these



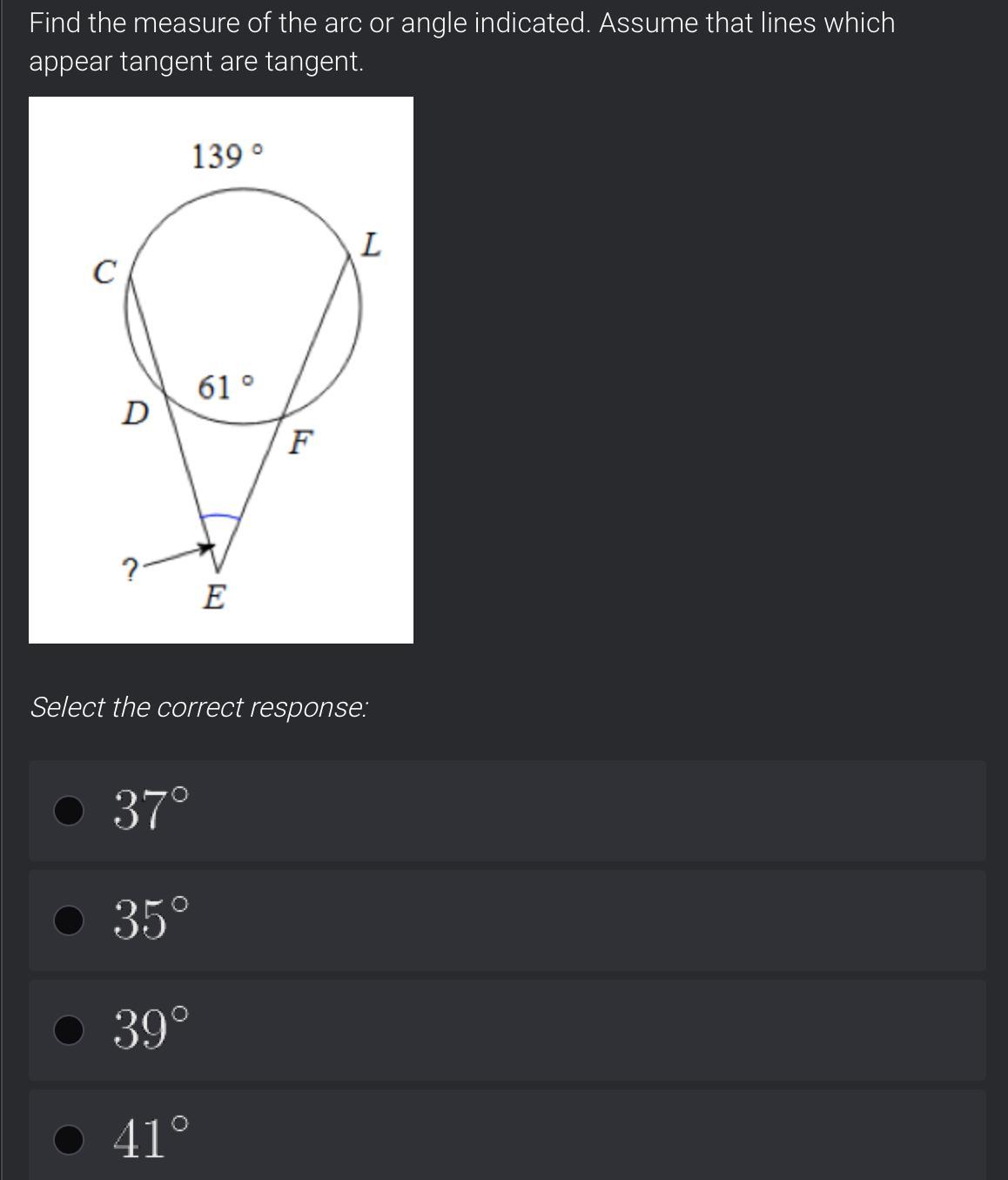

Answers
Answer:
The Correct answer is
57°
If LN=6x-35 and MN=19 and LM=5x-9,find x.

Answers
pls help me whats 45x57
Answers
Answer:
2565
Step-by-step explanation:
:)
Answer:
2565
Step-by-step explanation:
from a sample of 50 individuals, age 36-50, 25 individuals read newspapers to find out the news. from a sample of 50 individuals over age 50, 30 individuals read newspapers to find out the news. can we reject the null hypotheses that the news is read equally for both age groups? significance level is 5%.
Answers
The p-value is greater than the significance level of 0.05, we fail to reject the null hypothesis that the news is read equally for both age groups.
To test whether the proportion of individuals who read newspapers to find out the news is the same for both age groups, we can use a hypothesis test for two proportions. Let p1 be the true proportion of individuals who read newspapers in the age group 36-50, and let p2 be the true proportion of individuals who read newspapers in the age group over 50.
The null hypothesis is that the proportions are equal, i.e., H0: p1 = p2. The alternative hypothesis is that the proportions are not equal, i.e., Ha: p1 ≠ p2.
We can use a significance level of 5%, which means that we will reject the null hypothesis if the p-value is less than 0.05.
To conduct the test, we can calculate the sample proportions of individuals who read newspapers in each age group:
p-hat1 = 25/50 = 0.5
p-hat2 = 30/50 = 0.6
We can also calculate the pooled proportion, which is the weighted average of the two sample proportions:
p-hatp = (25 + 30) / (50 + 50) = 0.55
Using the sample proportions and the pooled proportion, we can calculate the test statistic:
z = (p-hat1 - p-hat2) / √(p-hatp × (1 - p-hatp) × (1/50 + 1/50))
= (0.5 - 0.6) / √(0.55 × 0.45 × (1/50 + 1/50))
= -1.52
The p-value for this test is the probability of getting a test statistic as extreme or more extreme than the observed value of -1.52, assuming the null hypothesis is true. Since this is a two-tailed test, we need to calculate the probability of getting a z-score less than -1.52 or greater than 1.52.
Using a standard normal table or a calculator with a normal distribution function, we can find the p-value:
p-value = P(Z ≤ -1.52) + P(Z ≥ 1.52) ≈ 0.129
Learn more about hypothesis tests at
https://brainly.com/question/30588452
#SPJ4
The circumference of the earth is given.
Circumference of earth: 24,901 miles
What is the diameter of earth? Round your answer to the nearest tenth. Use 3.14 for π.
Answers
Answer:
7930.3 miles = d
Step-by-step explanation:
The circumference equals
C = pi *d
24901 = 3.14 d
Divide each side by 3.14
24901 / 3.14 = d
7930.254777 = d
Rounding to the nearest tenth
7930.3 =d
Write the equation of the line that passes through the points (-3, -3) and (8,7). Put your answer in fully reduced point-slope form, unless it is a vertical or horizontal line.
Answers
Answer:
Step-by-step explanation:
First you want to find the slope
y2-y1/x2-x1
7-(-3)/8-(-3)
Two negatives equal a positive. so Rewrite
7+3/8+3
10/11
Slope=10/11
To find the equation of the line..
y-y1=10/11(x-x1)
y-(-3)=10/11(x-(-3)
Again double negative, so rewrite
y+3=10/11(x+3)
y+3=10/11x+30/11
Subtract three from both sides to isolate 'y'
y+3-3=10/11x+30/11-3
y=10/11x+30/11-3
y=10/11x-3/11
Draw an indifference map in each of the following situations: a. (3 marks) John eats eggs and toast for breakfast and insists on having three pieces of toast for every two eggs he eats. b. (3 marks) Xi spends her income on bread and chocolate. She views chocolate as a good but is neutral about bread. c. (3 marks) Ramesti considers tickets to the opera and to the baseball games to be perfect substitutes. d. (3 marks) Ahmad consumes chocolates and chips. However, he hates chocolates after eating 3 chocolate bars in the day.
Answers
a. John's indifference map would show a preference for combinations of eggs and toast where the ratio of toast to eggs is 3:2.
b. Xi's indifference map would show an equal preference for different combinations of bread and chocolate, as she is neutral about bread but views chocolate as a good.
c. Ramesti's indifference map would show perfect substitution between tickets to the opera and baseball games, indicating that he is equally satisfied with either option.
d. Ahmad's indifference map would show a diminishing marginal utility for chocolate bars, where his satisfaction decreases after consuming a certain number of chocolate bars in a day.
which is because:
John's indifference map would consist of curves or lines that represent combinations of eggs and toast where the ratio of toast to eggs is 3:2. Each curve or line represents a different level of satisfaction or utility for John. As he moves further away from his preferred ratio of 3:2, his satisfaction decreases.
Xi's indifference map would show straight lines or curves that represent combinations of bread and chocolate where she is indifferent between different combinations. Since she views chocolate as good and is neutral about bread, the lines or curves would be parallel to the chocolate axis, indicating that she values chocolate more than bread.
Ramesti's indifference map would consist of straight lines that represent perfect substitution between tickets to the opera and baseball games. Any combination of tickets along a line would provide the same level of satisfaction for Ramesti, indicating that he is willing to trade one ticket for the other at a constant rate.
Ahmad's indifference map would show a downward-sloping curve that represents diminishing marginal utility for chocolate bars. As he consumes more chocolate bars in a day, the curve would become flatter, indicating that the additional satisfaction he derives from each additional chocolate bar decreases. This reflects his dislike for chocolates after consuming a certain quantity.
Learn more about indifference maps here: https://brainly.com/question/31679440
#SPJ11
PLEASE PLEASE HELP ILL LIKE AND ITS WORTH 20 POINTS !!

Answers
Answer:
Left one: 27.755 Right one: 3487.5
Step-by-step explanation:
You have to use sin of angle to find the area.
Parker is in the business of manufacturing phones. He must pay a daily fixed cost to rent the building and equipment, and also pays a cost per phone produced for materials and labor. The equation C=175p+400 can be used to determine the total cost, in dollars, of producing pp phones in a given day. What is the y-intercept of the equation and what is its interpretation in the context of the problem?
Answers
9514 1404 393
Answer:
400; building and equipment fixed cost
Step-by-step explanation:
The cost equation has two terms. The constant term (400) is the daily fixed cost of building and equipment. The variable term (175p) represents the cost of producing p phones.
The y-intercept is 400. It is the daily fixed cost of the building and equipment.
Answer:
The y-intercept of the function is 400 which represents the fixed cost for rent and equipment.
Step-by-step explanation:
Since Parker must pay $400 even to make 0 phones, that means $400 is the fixed cost that Parker must pay for rent and equipment regardless of the number of phones produced.
Have a good day :)
What is the sum of all the positive two-digit integers where one of the digits is three times the other
Answers
The sum of all the positive two-digit integers where one of the digits is three times the other is 630.
To arrive at this result, the numbers can be broken down into two groups. The first group consists of numbers with 3 as the first digit, and the second group consists of numbers with 3 as the second digit.
For the first group, the sum is calculated by multiplying the 3 by all the numbers from 1 to 9. This gives a sum of 3+6+9+12+15+18+21+24+27 = 135.
For the second group, the sum is calculated by multiplying the 3 by all the numbers from 1 to 9 and then reversing the digits. This gives a sum of 30+60+90+12+51+81+21+42+72 = 495.
The total sum of all the positive two-digit integers where one of the digits is three times the other is 135+495 = 630.
For more questions like Integers click the link below:
https://brainly.com/question/490943
#SPJ4
A=(r+k/3)f solve for r
Answers
Answer:
R = (K/3) + (A/F)
Step-by-step explanation:
The goal is to isolate the r on one side.
The first step is to distribute the f on the right side of the equation.
a=rf+kr/3
Then, we should subtract rf from both sides
a-rf=kf/3
Next we need to subtract a from both sides
-rf=kf/3-a
Lastly, we should divide both sides by -f
r=-k/3+a/f
Simplify (7x2 + 3)(7x2 – 3) using the difference of squares formula.
Answers
The Solution:
Given:
\(\left(7x^2+3\right)\left(7x^2-3\right)\)Required:
Simplify the given expression using the difference of two squares.
The difference of two squares formula:
\(\)
. Betty has several of the standard six-sided dice that are common in many board games. If Betty rollsone of these dice, what is the probability that:A: She rolls a three. (enter the answer as a percent rounded to the nearest tenths place)B: She rolls a six. (enter the answer as a percent rounded to the nearest tenths place)C: She rolls a three or a six. (enter the answer as a percent rounded to the nearest tenths place)D: She rolls an even number (enter the answer as a percent rounded to the nearest tenths place
Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the formula for probability
\(Probability=\frac{number\text{ of required outcomes}}{number\text{ of total outcomes}}\)STEP 2: Wit the required data
\(\begin{gathered} For\text{ a standard six-sided die,} \\ The\text{ total outcomes is 6} \\ n(Total)=6 \end{gathered}\)STEP 3: Find the probability that she rolls a three
\(\begin{gathered} n(3)=1 \\ n(total)=6 \\ Pr(3)=\frac{1}{6} \\ To\text{ percentage:} \\ \frac{1}{6}\times100=16.6666667\approx16.7\% \end{gathered}\)The probability that she rolls a three is 16.7%
STEP 4: Find the probability that she rolls a six
\(\begin{gathered} n(6)=1 \\ n(total)=6 \\ Pr(6)=\frac{1}{6} \\ To\text{percentage} \\ \frac{1}{6}\times100=16.666,666,7\approx16.7\operatorname{\%} \end{gathered}\)The probability that she rolls a six is 16.7%
STEP 5: Find the probability that she rolls three or a six
\(\begin{gathered} Pr(3\text{ or 6\rparen}=Pr(3)+Pr(6) \\ =\frac{1}{6}+\frac{1}{6}=\frac{2}{6}=\frac{1}{3} \\ To\text{ percentage''} \\ \frac{1}{3}\times100=\frac{100}{3}=33.3333333\approx33.3\% \end{gathered}\)The probability that she rolls a three or six is 33.3%
STEP 6: Find the probability that she rolls an even number
\(\begin{gathered} Even\text{ number}=2,4,6 \\ n(even\text{ number\rparen}=3 \\ Pr(even\text{ number\rparen}=\frac{3}{6}=\frac{1}{2} \\ To\text{ percentage:} \\ \frac{1}{2}\times100=\frac{100}{2}=50\% \end{gathered}\)The probability that she rolls an even number is 50.0%
Solve the equation in standard form

Answers
The solutions to the equation -30x² + 9x + 60 = 0 are x = 5/2 and x = -4/5.
To solve the equation, we can start by bringing all the terms to one side to have a quadratic equation equal to zero. Let's go step by step:
-5/3 x² + 3x + 11 = -9 + 25/3 x²
First, let's simplify the equation by multiplying each term by 3 to eliminate the fractions:
-5x² + 9x + 33 = -27 + 25x²
Next, let's combine like terms:
-5x² - 25x² + 9x + 33 = -27
-30x² + 9x + 33 = -27
Now, let's bring all the terms to one side to have a quadratic equation equal to zero:
-30x² + 9x + 33 + 27 = 0
-30x² + 9x + 60 = 0
Finally, we have the quadratic equation in standard form:
-30x² + 9x + 60 = 0
Dividing each term by 3, we get:
-10x² + 3x + 20 = 0
(-2x + 5)(5x + 4) = -10x² + 3x + 20
So, the factored form of the equation -30x² + 9x + 60 = 0 is:
(-2x + 5)(5x + 4) = 0
Now we can set each factor equal to zero and solve for x:
-2x + 5 = 0 --> x = 5/2
5x + 4 = 0 --> x = -4/5
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
A car rental company charges $19.99 per day and $0.17 per mile. Write an expression that gives the total cost in dollars to rent a car for d days and m miles.
I WILL GIVE BRAINLIEST TO THE BEST ANSWER
Answers
please help me with this!! ( links= report )

Answers
Answer:
Step-by-step explanation:
parrelograpm (b*H)
40cm^2
Area of semi circle 1/2(pi)r^2
1/2(pi)(5)^2
39.26990
total?
40+39.26990=79.26990
is the expression x3 ∙ x3 ∙ x3 equivalent to x3 ∙ 3 ∙ 3? why or why not? explain your reasoning. source stylesnormalfontsize
Answers
The reasoning is that the exponents in the first expression indicate repeated multiplication of x3, while the second expression represents the product of x3, 3, and 3.
In the expression x3 ∙ x3 ∙ x3, the exponent 3 is applied to each instance of x, indicating repeated multiplication of x by itself three times. This can be simplified as x^(3+3+3) or x^9.
On the other hand, the expression x3 ∙ 3 ∙ 3 represents the product of x raised to the power of 3, multiplied by 3, and then multiplied by another 3. This simplifies to 3^2 x x^3 or 9x^3.
Therefore, the two expressions are not equivalent. In the first expression, the exponents are additive and result in x^9, whereas in the second expression, the exponents are separate and the 3s are multiplied, resulting in 9x^3.
It is crucial to pay attention to the properties of exponents and the correct interpretation of the given expressions to determine their equivalence or lack thereof.
Learn more about reasoning: brainly.com/question/25175983
#SPJ11
Two trains leave the station at the same time, one heading east and the other west. The eastbound train travels at 95 miles per hour. The westbound train travels at 115 miles per hour. How long will it take for the two trains to be 336 miles apart? Do not do any rounding.
Answers
Answer:
It will take 1.6 hours for the two trains to be 336 miles apart.
Step by step explanation:
Given that:
Speed of eastbound train = 95 miles per hour
Speed of westbound train = 115 miles per hour
Combined speed = 95+115 = 210 miles
Distance = 336 miles
\(Speed = \frac{Distance}{Time}\\\\210 = \frac{336}{Time}\\\\Time = \frac{336}{210}\\\\Time = 1.6\ hours\)
Hence,
It will take 1.6 hours for the two trains to be 336 miles apart.
You make an investment of $8000. For the first 18 months you earn 5% compounded semi-annually. For the next 5 months you earn 10% compounded monthly. What is the maturity value of the certificate?
Answers
The maturity value of the investment would be $8,858.80.
To calculate the maturity value, we need to calculate the compound interest for each period separately and then add them together.
For the first 18 months, the interest is compounded semi-annually at a rate of 5%. Since there are two compounding periods per year, we divide the annual interest rate by 2 and calculate the interest for each period. The formula for compound interest is A = P(1 + r/n)^(nt), where A is the maturity value, P is the principal amount, r is the annual interest rate, n is the number of compounding periods per year, and t is the number of years. Plugging in the values, we get A = 8000(1 + 0.05/2)^(2*1.5) = $8,660.81.
For the next 5 months, the interest is compounded monthly at a rate of 10%. We use the same formula but adjust the values for the new interest rate and compounding frequency. Plugging in the values, we get A = 8000(1 + 0.10/12)^(12*5/12) = $8,858.80.
Therefore, the maturity value of the certificate after the specified period would be $8,858.80.
Learn more about compound interest here:
https://brainly.com/question/22621039
#SPJ11
CAN SOMEONE PLS HELP ME ON THIS ONE.....

Answers
Answer:
Years 3-4 and the percentage change was by 8%. Please vote Brainliest!
Step-by-step explanation:
Answer:
C the greatest growth was between 3 and 4 and about 8%
Step-by-step explanation:
what is the constant proportionality of y=5/7x
Answers
Explanation:
I'm assuming the equation is \(y = \frac{5}{7}x\) which is the same as writing y = (5/7)x.
If so, then the constant of proportionality is the fraction out front: The value 5/7 is the coefficient of the term (5/7)x.
All direct proportion equations are of the form y = kx, where k is the constant of proportionality. Another example would be y = 12x and this time k = 12.
using the smallest number of pebbles possible and without using blue pebbles, what is the value in pebbles of 2 blue pebbles?
Answers
According to the combination, The value of the Two blue pebbles is a 3 red pebbles and 1 yellow pebbles.
According to the statement
We have to find that the value of the combination.
So, For this purpose, we know that the
A combination could be a mathematical technique that determines the quantity of possible arrangements in an exceedingly collection of things where the order of the choice doesn't matter.
From the given information:
A red pebble is capable 3 yellow pebbles. A blue pebble is adequate a red pebble and a couple of yellow pebbles. Therefore, the blue pebbles will be:
= 3 yellow pebble + 2 yellow pebbles
= 5 yellow pebbles or 15 red pebbles
And
Two blue pebbles will be:
= 10 yellow pebbles
= 3 red pebbles and 1 yellow pebbles.
So, According to the combination, The value of the Two blue pebbles is a 3 red pebbles and 1 yellow pebbles.
Learn more about Combination here
https://brainly.com/question/24756209
Disclaimer: This question was incomplete. Please find the content below.
Question:
A red pebble is equal to 3 yellow pebbles A blue pebble is equal to a red pebble and 2 yellow pebbles. A green pebble is equal to 3 red pebbles
Using the smallest number of pebbles possible and without using blue pebbles, what is the value in pebbles of 2 blue pebbles?
#SPJ4
dujuan bought a car for $ 17000 , and ever since the car's value has decreased exponentially by 17 % per year. how long will it take for the car's value to be $ 5000 ?
Answers
It will take approximately 8.84 years for the car's value to be $5000.
We can use the formula for exponential decay to find the time it takes for the car's value to reach $5000:
V = V0 * \(e^{(-rt)\)
where V is the current value, V0 is the initial value, r is the decay rate, and t is the time in years. We can rearrange this formula to solve for t:
t = -ln(V/V0) / r
Plugging in the given values, we get:
t = -ln(5000/17000) / (-0.17) = 8.84 years (rounded to two decimal places)
Therefore, it will take approximately 8.84 years for the car's value to be $5000.
Learn more about exponential Decay:
https://brainly.com/question/24077767
#SPJ4
Can somebody help me? Will mark brainliest.

Answers
Answer:
4
Step-by-step explanation:
Given the triangle AEC - trianhle BED the 4th equation, ED/EC = AC/BD is true.
what is the value sin 35 = 20/x
Answers
Answer:
I got x=4/7
Step-by-step explanation:
hoped I helped:) please correct me if in wrong:)
Which property of multiplication is shown? x = x • 1 Group of answer choices
Answers
Identity Property of Multiplication
Exercise Oo.: Carter's desk lamp uses a lightbulb that has an exponential life- time with a mean of 6 months. When the lightbulb goes out, it is immediately replaced. It is now New Year's Eve. What is the probability that exactly three bulbs will be replaced before the end of March?
Answers
The probability of exactly three bulbs being replaced before the end of March is approximately 0.0126 or 1.26%.
To solve this problem, we need to use the exponential distribution formula:
f(x) = (1/β) * e^(-x/β)
where β is the mean and x is the time period.
In this case, β = 6 months, and we need to find the probability of exactly three bulbs being replaced before the end of March, which is three months from New Year's Eve.
So, we need to find the probability of three bulbs being replaced within three months, which can be calculated as follows:
P(X = 3) = (1/6)^3 * e^(-3/6)
= (1/216) * e^(-0.5)
≈ 0.011
Therefore, the probability that exactly three bulbs will be replaced before the end of March is approximately 0.011.
To answer this question, we will use the Poisson distribution since it deals with the number of events (in this case, lightbulb replacements) occurring within a fixed interval (the time until the end of March). The terms used in this answer include exponential lifetime, mean, Poisson distribution, and probability.
The mean lifetime of the lightbulb is 6 months, so the rate parameter (λ) for the Poisson distribution is the number of events per fixed interval. In this case, the interval of interest is the time until the end of March, which is 3 months.
Since the mean lifetime of the bulb is 6 months, the average number of bulb replacements in 3 months would be (3/6) = 0.5.
Using the Poisson probability mass function, we can calculate the probability of exactly three bulbs being replaced (k = 3) in the 3-month period:
P(X=k) = (e^(-λ) * (λ^k)) / k!
P(X=3) = (e^(-0.5) * (0.5^3)) / 3!
P(X=3) = (0.6065 * 0.125) / 6
P(X=3) = 0.0126
So the probability of exactly three bulbs being replaced before the end of March is approximately 0.0126 or 1.26%.
To learn more about probability, click here:
brainly.com/question/30034780
#SPJ11
4(x-2)+5x=7x-14 find x
Answers
Answer:
x = -3
Step-by-step explanation:
Answer:
x= -11
Step-by-step explanation:
you multiple 4 times the things in the parentheses and solve for x