What do 14 and 18 have in common?
Answers
Related Questions
which linear equation represents the data given in the table?

Answers
Answer:
\(c \: \: y = 3x - 8\)
if you insert x and y value in equation you can find equation
a uniformly charged thin rod lies along the x axis from x = 0 to x = +[infinity].
Answers
In this scenario, we have a uniformly charged thin rod extending along the x-axis from the origin (x = 0) to positive infinity (x = +∞).
The term "uniformly charged" means that the charge is distributed evenly throughout the entire length of the rod.
To analyze this situation, we can consider the following steps: 1. Determine the linear charge density (λ) of the rod. Since the rod is uniformly charged, λ remains constant along its entire length. λ is usually given in units of charge per length (e.g., coulombs per meter).
2. To find the electric field at a particular point along or outside the rod, we can break the rod into infinitesimally small segments (dx) and consider the contribution of the electric field (dE) from each of these segments.
3. Calculate the electric field (dE) produced by each segment at the desired point using Coulomb's equations , considering the linear charge density (λ) and distance between the segment and the point.
4. Integrate the electric field contributions (dE) from all segments along the entire length of the rod (from x = 0 to x = +∞) to find the total electric field (E) at the point of interest.
By following these steps, you can analyze the electric field and related properties of a uniformly charged thin rod extending along the x-axis from x = 0 to x = +∞.
To know more about equation click here
brainly.com/question/649785
#SPJ11
The coordinate grid shows points A through K. What point is a solution to the system of inequalities? y > −2x + 10 y > 1/2x − 2 coordinate grid with plotted ordered pairs, point A at negative 5, 4 point B at 4, 7 point C at negative 2, 7 point D at negative 7, 1 point E at 4, negative 2 point F at 1, negative 6 point G at negative 3, negative 10 point H at negative 4, negative 4 point I at 9, 3 point J at 7, negative 4 and point K at 2, 3
answer:
a) E
b) K
c) B
d) D
Answers
Based on the analysis, point D at (-7, 1) is the only solution to the system of inequalities y > -2x + 10 and y > (1/2)x - 2. Therefore, the correct answer is option d) D.
To determine which point is a solution to the system of inequalities y > -2x + 10 and y > (1/2)x - 2, we can test each point to see if it satisfies both inequalities.
a) Point E at (4, -2):
Substituting the coordinates into the inequalities:
-2 > -2(4) + 10 -> -2 > -8 + 10 -> -2 > 2 (False)
-2 > (1/2)(4) - 2 -> -2 > 2 - 2 -> -2 > 0 (False)
b) Point K at (2, 3):
Substituting the coordinates into the inequalities:
3 > -2(2) + 10 -> 3 > -4 + 10 -> 3 > 6 (False)
3 > (1/2)(2) - 2 -> 3 > 1 - 2 -> 3 > -1 (True)
c) Point B at (4, 7):
Substituting the coordinates into the inequalities:
7 > -2(4) + 10 -> 7 > -8 + 10 -> 7 > 2 (True)
7 > (1/2)(4) - 2 -> 7 > 2 - 2 -> 7 > 0 (True)
d) Point D at (-7, 1):
Substituting the coordinates into the inequalities:
1 > -2(-7) + 10 -> 1 > 14 + 10 -> 1 > 24 (False)
1 > (1/2)(-7) - 2 -> 1 > -3.5 - 2 -> 1 > -5.5 (True)
Based on the analysis, point D at (-7, 1) is the only solution to the system of inequalities y > -2x + 10 and y > (1/2)x - 2. Therefore, the correct answer is option d) D.
For more questions on inequalities
https://brainly.com/question/1870140
#SPJ11
U.S. Population can be modeled by the function f(x)=165.6x^1.345, where f(x) is in thousand and x is the number of year after 1800. What is f(50) and what does it mean?
Answers
Answer:
f(50) = 31928.24 thousands
Therefore, it means that the US population in year 1850 is 31928.24 thousands
Step-by-step explanation:
Given the function;
f(x)=165.6x^1.345
Where;
f(x) is in thousand and
x is the number of year after 1800
To determine f(50), we will substitute x = 50 into the function of f(x);
f(50)=165.6(50)^1.345
f(50) = 31928.24 thousands
Since f(50) is the US population in year 1800+50 = 1850
Therefore, the US population in year 1850 is 31928.24 thousands
n a regression analysis of on-the-job head injuries of warehouse caused by falling[30] objects, y is a measure of severity of the injury, x1 is an index reflecting both the weight of the object and the distance it fell, and x2 and x3 are indicator variables for nature of head protection worn at the time of the accident, coded as follows:
Answers
The regression analysis of on-the-job head injuries of warehouse caused by falling objects involves the use of x1 to predict the severity of the injury and x2 and x3 to predict the severity of the injury .
Regression analysis is used to determine the relationship between the independent variable(s) and the dependent variable(s).
In this particular analysis, the focus is on the on-the-job head injuries of warehouse caused by falling objects.
The independent variables of this analysis include x1, x2 and x3 while the dependent variable is y. X1 is an index reflecting both the weight of the object and the distance it fell.
This variable can be used to predict the severity of the injury. If the object is heavy and falls from a great height, it is likely to cause more severe injuries as compared to when it falls from a lower height and is lighter in weight.
X2 and x3 are indicator variables for nature of head protection worn at the time of the accident. These variables are coded as follows: 0 - head protection not worn and 1 - head protection worn.
These variables can be used to predict the severity of the injury in case head protection was not worn. When head protection is not worn, there is a high probability of the injuries being more severe as compared to when it is worn.
In conclusion, the regression analysis of on-the-job head injuries of warehouse caused by falling objects involves the use of x1 to predict the severity of the injury and x2 and x3 to predict the severity of the injury in cases where head protection was not worn.
The results of this analysis can be used to identify areas of weakness in terms of safety and to
develop interventions aimed at reducing the incidence and severity of such injuries.
To know more about Regression visit:
https://brainly.com/question/32505018
#SPJ11
Enter the data to create a histogram and use the drop-down menus to complete the statements.
A 1-column table with 9 rows. Column 1 is labeled Dollar-sign with entries 7, 11, 8, 14, 9, 9, 10, 9, 10.
Liv keeps track of how much money she makes every time she babysits.
The peak at
tells us the amount of money Liv makes
.
No bar at
means Liv never made between
.
Answers
Answer:
8-9 , most often , 12-13, and 12-13
Step-by-step explanation:
TBH, i am not sure what im doing. Here is a pic of the question.

Answers
Answer:
7
Step-by-step explanation:
The order of operations tells you to start any evaluation by looking at the innermost set of parentheses first.
Here, that means your first step is to find the value of h(-3). You do that by finding the input (x) value -3 in the table for h(x), and locating the corresponding output, h(x), which is 2.
Now, the problem becomes evaluating g(2).
You do the same thing for that function: locate the input x=2 in the table for g(x) and find the corresponding output: 7.
Now, you know ...
g(h(-3)) = g(2) = 7
Please help I’ve been trying to get answers for days now :/

Answers
Answer:
If the whole box is the sports store then its just 80m if its just the equipment section then its 56m
Step-by-step explanation:
8x10=80
80-(6x4)=56 80-24=56
Kyle and Myles wanted to buy the soccer team food after the game.
Kyle bought 5 hotdogs and 3 French fries, which costs him $14.50. Myles bought 4 hotdogs and 2 French fries, which totaled as $11.00. How much does 1 hotdog cost?
Walkthrough your answer by showing your work
Answers
Set up 2 equations:
Kyle: 5h + 3f = 14.50
Myles: 4h + 2f = 11.00
Lets get the two h's to cancel out.
Multiply Kyle by 4 and Myles by -5:
Kyle: 20h + 12f = 58
Myles: -20h - 10f = -55
Now add the two equations together:
2f = 3
Divide both sides by 2:
f = 3/2
f = 1.50
1 french fry cost $1.50
Now solve for the price of a hot dog:
5h + 3(1.50) = 14.50
5h + 4.50 = 14.50
Subtract 4.50 from both sides:
5h = 10.00
Divide both sides by 5:
h = 2
One hot dog cost $2.00
The table shows a probability distribution P(X) for a discrete random variable X. What is P(X>2)?

Answers
Answer:
0.30
Step-by-step explanation:
You want P(x > 2) given the probability distribution table shown.
Greater than 2There are two table entries where X > 2. One of them has a probability of 0.14, and the other a probability of 0.16. They are mutually exclusive, so the probabilities add.
P(x > 2) = P(x = 3) + P(x = 4) = 0.14 +0.16
P(x > 2) = 0.30
<95141404393>
Choose the correct simplification of 9x2(4x 2x2 − 1). 18x4 36x3 − 9x2 18x4 − 36x3 9x2 36x4 18x3 − 9x2 36x4 − 13x3 9x2
Answers
The correct simplification would be \(18x^4 - 36x^3 + 9x^2\) (option a).
To simplify the expression \(9x^2(4x - 2x^2\) - 1), we need to perform the multiplication and combine like terms.
1. Start by distributing the 9x^2 to each term inside the parentheses:
\(9x^2 * 4x = 36x^3 9x^2 * (-2x^2) = -18x^4 9x^2 * (-1) = -9x^2\)
2. Now we can combine the terms obtained from the distribution:
\(36x^3 - 18x^4 - 9x^2\)
3. Rearranging the terms in descending order of exponents:
\(-18x^4 + 36x^3 - 9x^2\)
4. However, we can simplify this expression further by factoring out a common factor of \(-9x^2\):
\(-9x^2(2x^2 - 4x + 1)\)
5. Thus, the final simplified expression is:
\(18x^4 - 36x^3 + 9x^2\)
For more such questions on simplification, click on:
https://brainly.com/question/723406
#SPJ8
The diagonal of a tv screen is 26 inches. the base is 18.8 inches wide. how tall is the tv?
Answers
the height of the triangle formed by the diagonal and base of the TV screen.
The height of the TV is approximately 15.6 inches.
(26 inches / √2) = 18.8 inches
(18.8 inches * √2) = 26 inches
Height = (26 inches / 18.8 inches) * 18.8 inches
Height = 15.6 inches
Step 1: Calculate the hypotenuse of the triangle formed by the diagonal and base of the TV screen.
Hypotenuse = diagonal / √2
Hypotenuse = 26 inches / √2
Hypotenuse = 18.8 inches
Step 2: Calculate the diagonal of the triangle formed by the hypotenuse and base of the TV screen.
Diagonal = hypotenuse * √2
Diagonal = 18.8 inches * √2
Diagonal = 26 inches
Step 3: Calculate the height of the triangle formed by the diagonal and base of the TV screen.
Height = diagonal / base
Height = 26 inches / 18.8 inches
Height = 15.6 inches
Learn more about height here
https://brainly.com/question/10726356
#SPJ4
what is 2b^3+5=2(3)^3+5=
Answers
Answer:
the final answer is three.
the last step is finding the cube root of 27

Answer:
59
Step-by-step explanation:
−5 ×7+ 10/2 equals what pls help me
Answers
Answer:
-30
Step-by-step explanation:
-5 times 7 is -35
-35 plus 10/2 10/2=5
-35+5=-30
Answer:
Hello! :) have a good day!
-5 x 7 + 10/2 = -30
Students arrive at the Administrative Services Office at an average of one every 15 minutes, and their requests take on average 10 minutes to be processed. The service counter is staffed by only one clerk, Judy Gumshoes, who works eight hours per day. Assume Poisson arrivals and exponential service times.a. What percentage of time is Judy idle? (Round your answer to 2 decimal places.)Percentage of time %b. How much time, on average, does a student spend waiting in line? (Round your answer to the nearest whole number.)Average time minutesc. How long is the (waiting) line on average? (Round your answer to 2 decimal places.)Average waiting line studentsd. What is the probability that an arriving student (just before entering the Administrative Services Office) will find at least one other student waiting in line? (Round your answer to 4 decimal places.)Probability
Answers
a. Judy is idle 33.33 percent of the time
b. The average time a student spends waiting in line isLq = [(2/3)² + (1/15)²]/[2(1/15)(1/3)] - (1/10)= 0.4 hours = 24 minutes
c. The average waiting line length is 2 students
d. The probability of finding at least one student in the system is given byP(L>0) = ρ = λ/µ = (1/15)/(1/10) = 0.6667P(L > 0) = 0.6667, rounded to four decimal places, gives 0.6667 as the probability that a student will find at least one other student waiting in line just before entering the Administrative Services Office.
(Round your answer to 2 decimal places.)Percentage of time %In this case, we have average arrival and processing times given. By Poisson arrivals and exponential service times, the clerk's queue is also a Poisson process with parameter λ = 1/15 (students per minute) and parameter µ = 1/10 (students per minute).The idle time percentage for Judy is given byρ = λ/µ= (1/15)/(1/10) = 2/3Judy's idle time proportion = 1 - ρ = 1 - 2/3 = 1/3 Therefore, Judy is idle 33.33 percent of the time.
(Round your answer to the nearest whole number.)Average time minutes The average waiting time for the queueing system isW = (ρ² + λ²)/[2 λ (1 - ρ)]The average waiting time for a student is then Lq = W - (1/µ)Thus, the average time a student spends waiting in line isLq = [(2/3)² + (1/15)²]/[2(1/15)(1/3)] - (1/10)= 0.4 hours = 24 minutes
(Round your answer to 2 decimal places.)Average waiting line studentsThe waiting line is the average number of students in the system minus the average number of students in service. As a result, the average waiting line length is given byL = ρ/(1 - ρ) = (2/3)/(1 - 2/3) = 2 studentsTherefore, the average waiting line length is 2 students
(Round your answer to 4 decimal places.)Probability The probability of finding at least one student in the system is given byP(L>0) = ρ = λ/µ = (1/15)/(1/10) = 0.6667P(L > 0) = 0.6667, rounded to four decimal places, gives 0.6667 as the probability that a student will find at least one other student waiting in line just before entering the Administrative Services Office.
Learn more about Probability
brainly.com/question/30034780
#SPJ11
solve: 4y - 6 = 2y + 8
Answers
Answer:
y = 7
Step-by-step explanation:
Given
4y - 6 = 2y + 8 ( subtract 2y from both sides )
2y - 6 = 8 ( add 6 to both sides )
2y = 14 ( divide both sides by 2 )
y = 7
a meter in a taxi calculates the fare using the function f(x)=2.56x+2.40. if x represents length what in miles can a passenger travel for $20
Answers
A passenger can travel approximately 6.875 miles for $20.
What is function?An input and an output are connected by a function. It functions similarly to a machine with an input and an output. Additionally, the input and output are somehow connected. The traditional format for writing a function is f(x) "f(x) =... "
We want to find the distance (in miles) that a passenger can travel for $20. Let's call this distance d.
Using the given function, we can set up an equation:
20 = 2.56d + 2.40
Solving for d:
2.56d = 20 - 2.40
2.56d = 17.60
d = 6.875
Therefore, a passenger can travel approximately 6.875 miles for $20.
Learn more about function on:
https://brainly.com/question/10439235
#SPJ1
helpppp 2x-1>5 and 3x-5<19

Answers
Answer:
3 < x < 8
Step-by-step explanation:
Solve each part separately
2x - 1 > 5 ( add 1 to both sides )
2x > 6 ( divide both sides by 2 )
x > 3 , that is
3 < x
and
3x - 5 < 19 ( add 5 to both sides )
3x < 24 ( divide both sides by 3 )
x < 8
Then putting the two together
3 < x < 8
5.075 as a mixed number
Answers
Answer:
5\(\frac{3}{40}\)
Step-by-step explanation:
Answer: 5 3/40
explanation: did you mean a mixed fraction or nah?
Solve using the quadratic formula. Show all work. Write each solution in simplest form. No decimals.

Answers
Answer:
D
Step-by-step explanation:
For a quadratic equation ax² +bx +c= 0, the quadratic formula is as below:
\(\boxed{x = \frac{ - b± \sqrt{ {b}^{2} - 4ac } }{2a} }\)
x² -12x +7= 0
\(x = \frac{ - ( - 12)± \sqrt{( - 12) {}^{2} - 4(1)(7) } }{2(1)} \)
\(x = \frac{12± \sqrt{144 - 28} }{2} \)
\(x = \frac{12± \sqrt{116} }{2} \)
\(x = \frac{12± \sqrt{4(29)} }{2} \)
\(x = \frac{12±( \sqrt{4})( \sqrt{29} )}{2} \)
\(x = \frac{12±2 \sqrt{29} }{2} \)
\(x = 6± \sqrt{29} \)
\(∴x = 6 + \sqrt{29} \: \: \: or \: \: \:x = 6 - \sqrt{29}\)
Find the measure of the arc or central angle indicated. Assume that lines which appear to be diameters are actual diameters. Do not include units in your answer (degrees, degree symbols, etc) (FR) *
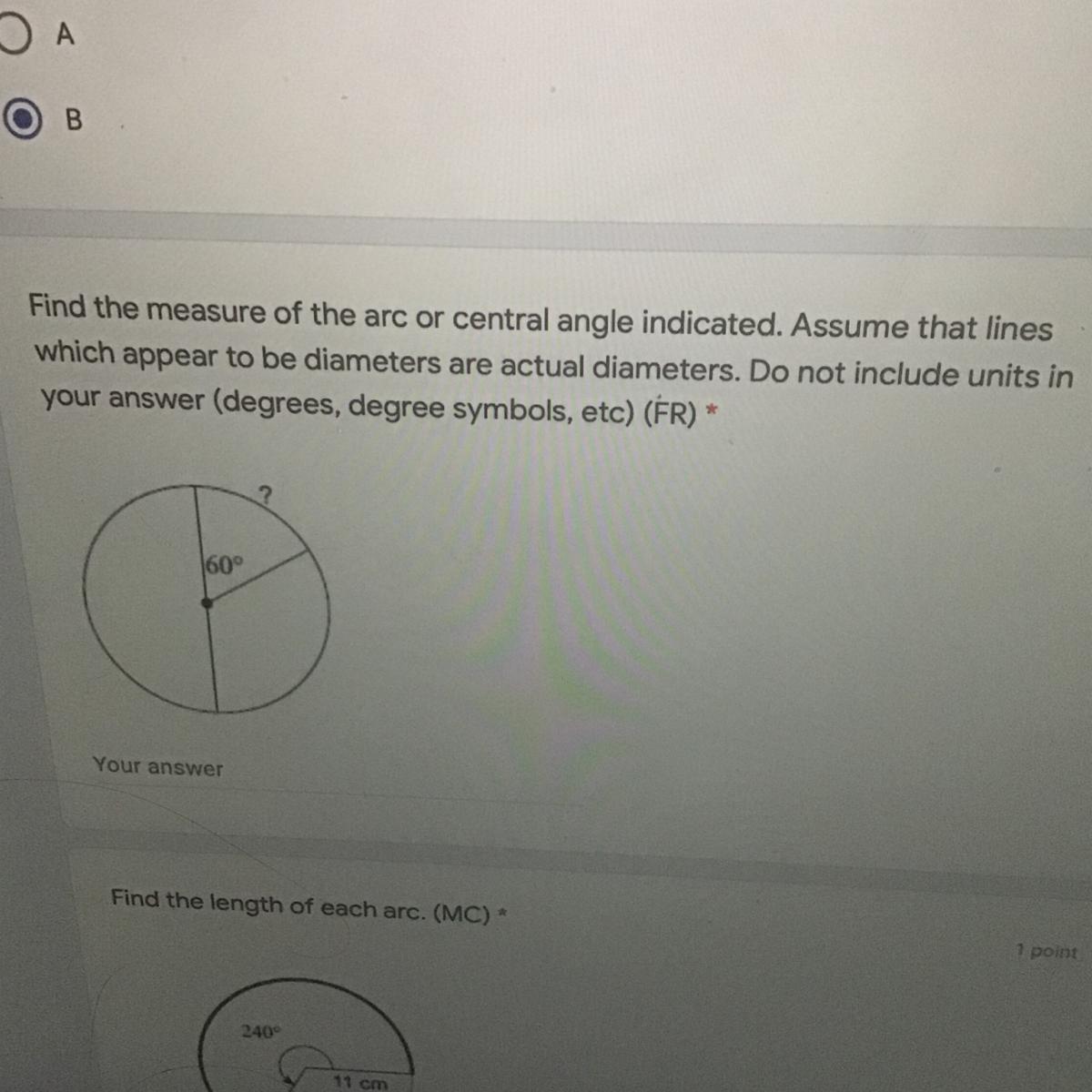
Answers
Answer:
60
Step-by-step explanation:
Central angle = intercepted arc
35 = 2b + 5b pls help
Answers
Step-by-step explanation:
2b+5b=7b
35=7b
35/7=5
b=5
Answer:
b=5
Step-by-step explanation:
2b+5b=35
7b=35
b=35/7
b=5
1. If a biker travels at a rate of 1/5 mile each minute, what is his rate in miles per hour?

Answers
HELP! WILL GIVE BRAINLEST! In a right triangle, sin(β) = 0.292. If the hypotenuse of the triangle has a length of 17.5 cm, what is the length of the side adjacent to angle β. Note: You will also need to use the Pythagorean theorem to answer this question.
16.7 cm
5.1 cm
11.4 cm
4.1 cm
Answers
Applying the sine ratio and the Pythagorean theorem, the adjecent length to angle β is: A. 16.7 cm.
What is the Sine Ratio?The sine ratio is given as, sin ∅ = opposite/hypotenuse.
Given the following in a right triangle:
∅ = β sin(β) = 0.292Hypotenuse = 17.5 cmFind the opposite side by applying the sine ratio:
0.292 = opp/17.5
Opposite = (0.292)(17.5)
Opposite = 5.11
Using the Pythagorean theorem, we have:
Adjacent length = √(17.5² - 5.11²)
Adjacent length = 16.7 cm.
Thus, applying the sine ratio and the Pythagorean theorem, the adjecent length to angle β is: A. 16.7 cm.
Learn more about the sine ratio on:
https://brainly.com/question/2920412
elana sells 3a adult tickets if elana sells 15 adult tickets does she sell at least 100 total tickets
Answers
Given that Elana sells 3a adult tickets. The number of adult tickets that Elana sells is 15. The question is whether Elana sells at least 100 total tickets.
Elana sells 3a adult tickets, where a is the number of tickets sold. Therefore, the number of adult tickets Elana sells is 3a = 15. Dividing both sides by 3, we geta = 5So, Elana sells 5 adult tickets. To find out whether Elana sells at least 100 tickets, we need to know the number of non-adult tickets sold.
If we assume that all tickets are either adult or non-adult, we can say that the total number of tickets sold is 5 + n, where n is the number of non-adult tickets sold. Since we don't know the value of n, we cannot determine if the total number of tickets sold is at least 100. Thus, the answer to the question is not clear from the information provided.
Know more about Dividing both sides here:
https://brainly.com/question/14534440
#SPJ11
On a map with a scale of 1 : 50000 , the distance between two adjacent farmhouses is 3.2cm.What is the corresponding distance on the ground in kilometers.(
Answers
Answer:
1.6 kilometres
Step-by-step explanation:
Well, multiply 3.2cm with 50000 and there's your answer. That's the point of the scale, it gives you a quick and easy way to convert distances on the map to distances in nature.
I'll make it even easier for you, I'll convert to kilometers. You have centimeters on map, so take 2 zeros off and you have meters, take 3 more zeros off, and you have kilometers. That makes it 3.2*0.5 which is 1.6 kilometers, or approximately one american imperial mile.
Please help genius people
One leg of an isosceles right triangle measures 11 inches. What is the approximate length of the hypotenuse?
Answers
Answer:
since it is isosceles right triangle, both legs = 5 inches.
using pythagoras theorem,
hypotenuse^2 = 5^2 +5^2 = 25+25 = 50 taking square root on both sides, hypotenuse = sqrt 50 = 5 sqrt 2 or 7.071
rounded to nearest tenth, length of hypotenuse is 7.1 inches.
Step-by-step explanation:
yan lang alam ko ʘ‿ʘ
Answer: 15.5 inches
Step-by-step explanation:
We’re accepting that legs = 11 inches.
hypotenuse^2 = 11^2+ 11^2 = 121+121 = 242 taking square root on both sides, hypotenuse = √242 => 11√2 or 15.5 inches.
!!PLS HELP ASAP!!30 POINTS!!
Divide using synthetic division
\(x^4-3x^3-7x+1\)÷\(x+2\)
Answers
The quotient and remainder are x³ -5x² + 10x - 17 and 55.
What is Synthetic division?
When the divisor is a linear factor, synthetic division is a technique used to carry out the division operation on polynomials.
Here, (x+2) is a linear factor which indicates that synthetic division can be applied.
So, we will divide the x^4 - 3x^3 - 7x + 1 by x+2.
(refer the attached solution)
Learn more about Polynomials from the given link:
https://brainly.com/question/29638766
#SPJ1
![!!PLS HELP ASAP!!30 POINTS!!Divide using synthetic division[tex]x^4-3x^3-7x+1[/tex][tex]x+2[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/8yprsebfa86csj8Wx4vXMSdg67ka61bd.jpeg)
solve using inverse operations 83+q=125; q=
Answers
Answer:
42
Step-by-step explanation:
83+q=125
q=125-83
q=42
) assembly comprises 769 team members. given that tmm operates two shifts a day, and assembly has 353 stations, what is the proportion of team members not assigned to one of the stations?
Answers
Among the 769 team members, 706 of them are assigned to operates in 2 shifts schedule. The proportion of team members not assigned to one of the stations is 63 / 769
Proportion means a share from total set being discussed.
Data from the given case:
- The assembly has 769 team members.
- The assembly has 353 stations
- At each station, there are 2 shifts operations.
Assuming that 1 person is assigned to 1 shift operation, then there will:
353 x 2 = 706 person assigned.
The remaining team members that not assigned is:
769 - 706 = 63 person.
Therefore, the share or the proportion of unassigned team members is:
63/769
Learn more about proportion here:
https://brainly.com/question/25640375
#SPJ4