What are the values of a, b, and c in the equation-2x squared +4x-3=0
Answers
The coefficients of the given quadratic equation are:
a = -2b = 4c = -3What are the values of a, b, and c?
Here we want to find the coefficients for the following quadratic equation:
-2x^2 + 4x - 3 = 0
Now, the general quadratic equation is written as:
a*x^2 + b*x + c = 0
So the two equations are:
-2x^2 + 4x - 3 = 0
a*x^2 + b*x + c = 0
So c is the constant term, comparing this with the given quadratic equation, we can see that:
c = -3
b is on the linear term, ad we can see that:
b = 4
a is on the quadratic term, we can see that:
a = -2
Learn more about quadratic equations:
https://brainly.com/question/1214333
#SPJ1
Related Questions
A garden has an area of 20 square feet. of the following choices, which is the smallest possible perimeter of the garden?
Answers
Answer:
the garden is approx 18 feet.
Step-by-step explanation:
A garden has an area of 20 square feet. of the following choices, which is the smallest possible perimeter of the garden?
Determine the total number of roots of each polynomial function.
f (x) = 3x6 + 2x5 + x4 - 2x3
6
g(x) = 5x - 12x2 + 3
2
f (x) = (3x4 + 1)2
8
g(x) = (x - 5)2 + 2x3
3
here are the answers hope this helps
Answers
The total number of roots of each polynomial function as required in the task content are as follows;
f (x) = 3x⁶ + 2x⁵ + x⁴ - 2x³ has 6 roots.g(x) = 5x - 12x² + 3 has 2 roots.f(x) = (3x⁴ + 1)² has 8 roots.g(x) = (x - 5)² + 2x³ has 3 roots.What are the total number of roots for each of the given functions?The degree of a polynomial very much determines the number of roots such polynomial function would have.
In this light, if the degree of a polynomial function, P(x) is n; it follows that the total number of roots of the function is; n.
The number of roots of the polynomial function are therefore as follows;
For f(x) = 3x⁶ + 2x⁵ + x⁴ + 2x³
Since the degree is 6; Total number of roots = 6.
For g(x) = 5x - 12x² + 3
Since the degree is 2 as it is a quadratic function; Total number of roots = 2.
For f(x) = (3x⁴ + 1)² = 9x⁸ + 6x⁴ + 1
Since the degree is 8; Total number of roots = 8.
For g(x) = (x - 5)² + 2x³
Since the degree is 3; Total number of roots = 3.
Ultimately, the total number of roots for each of the given functions are as listed above.
Read more on total number of roots of a polynomial function;
https://brainly.com/question/10345879
#SPJ1
This isnt an answer but a thank you, Thank yooouuuuuu
What is the slope-intercept for Y-5 =-3x+2
Answers
Answer:
-5/3
Step-by-step explanation:
Brianna makes $9.60 per hour. She works 5 hours and 40 minutes on Saturday. On Sunday, she worked for 1 hour and 10 minutes less than she did on Saturday. How much money did Brianna make combined on Saturday and Sunday?
Answers
Answer:
93.12
Step-by-step explanation:
If brianna works 5 hours and 40 minutes on saturday. you can turn this into a decimal. The decimal would obviously be 5.40
5.40 x 9.60 = 51.84 on saturday
Like saturday. you can do the same thing and turn them both into decimals.
5-1 means she would have 4 weeks
40- 10 would man she works 30 minutes
4.30 x 9.20 = 41.28 on sunday
41.28 + 51.84 = 93.12
Why median is better than mean?
Answers
Median is better than mean as it is not affected by extremely high or low values in the same way that the mean is
The median is a measure of central tendency, like the mean, but it is not affected by extremely high or low values in the same way that the mean is. Because of this, the median is often a better measure of central tendency when there are outliers in the data, or when the data is skewed (not normally distributed). For example, consider the following set of numbers: 1, 2, 3, 100. The mean of these numbers is 26, but the median is 3, which is a better representation of the "typical" value in this set.
However, the mean is still a useful measure and has its own advantages. For example, the mean is sensitive to every value in the data set, so it can provide a more comprehensive summary of the data. Additionally, the mean is easier to work with mathematically than the median, so it is often used in statistical tests and calculations.
Learn more about median here: brainly.com/question/14532771
#SPJ4
solve attachment EASY POINTS

Answers

Answer:
Same as the other guy
Step-by-step explanation:

what is the probability of not rolling a 3 on a six sided die
Answers
Answer:
Step-by-step explanation:
5/6
Answer:
5/6 or approximately 0.8333 (83.33%)
Step-by-step explanation:
This is because there are five possible outcomes that are not a 3 (1, 2, 4, 5, 6) out of a total of six possible outcomes.
On a plane, 2/5 of the passengers were British. 30% of the British passengers were men. There were 36 British men on the plane. Find the total number of passengers on the plane
Answers
Answer:
76 passengers
Step-by-step explanation:
100-36 is 64 and that makes 64 + 36 =100-30 is 70% and we have 36 + 40 =76
There were 300 passengers.
What is Algebra?Algebra is the branch of mathematics that helps in the representation of problems or situations in the form of mathematical expressions.
Given:
Fraction of British = 2/5
Percent of British men = 30%
Number of British men = 36
let the British passenger be x
30 /100 * x= 36
x=120
and let the total passenger by y
2/5 of y = 120
y= 120 * 5/2
x= 300
Hence, there were 300 passengers.
Learn more about algebra here:
https://brainly.com/question/24875240
#SPJ5
"Month 1 2 3 4 5 6 7
Value 23 15 20 12 18 22 15
What type of pattern exists in the data?
(a) positive trend pattern
(b) horizontal pattern
(c) vertical pattern
(d) negative trend pattern
Answers
The negative trend pattern exists in the given data.
The Given information is as follows: Month 1 2 3 4 5 6 7
Value 23 15 20 12 18 22 15
To find: What type of pattern exists in the data
The pattern that exists in the given data can be determined by creating a graph between month and value. So, the graph will be as follows: Type of pattern: From the above graph, it is evident that there is a Negative trend pattern in the data. Answer: (d) Negative trend pattern.
Conclusion: Thus, the negative trend pattern exists in the given data.
To know more about negative visit
https://brainly.com/question/1929368
#SPJ11
Find Any value of c for which the system has exactly one solution. Then solve the system using the value of c that you chose. Explain each step of your solution.
y=-x-4
3y = cx-19
Answers
Answer:
c = 4
Step-by-step explanation:
Given system of linear equations:
\(\begin{cases}y=-x-4\\3y=cx-19\end{cases}\)
A system of linear equations will have infinite solutions if the two equations are equivalent.
A system of linear equations will have no solutions if the two equations have the same slope (i.e. parallel lines).
A system of linear equations will have one solution if the equations are different, yet the substitution of the same x-value yields the same y-value in both equations.
Rewrite the second equation to isolate y:
\(\implies y=\dfrac{c}{3}x-\dfrac{19}{3}\)
Therefore, the y-intercept of the first equation is -4 and the y-intercept of the second equation is -19/3.
No value of "c" can make the second equation equivalent to the first equation since the y-intercepts are different.
To find the value of "c" where there are no solutions, equate the slopes of both equations and solve for c:
\(\implies \dfrac{c}{3}=-1\)
\(\implies c=-3\)
Therefore, if c = -3, the slopes of the two lines will be the same and there will be no solutions. So "c" cannot equal -3.
Therefore, for there to be exactly one solution for the given system of linear equations, "c" can be any value except -3.
Let's choose c = 4 as an example.
Therefore:
\(\begin{cases}y=-x-4\\3y=4x-19\end{cases}\)
Substitute the first equation into the second equation and solve for x:
\(\implies 3(-x-4)=4x-19\)
\(\implies -3x-12=4x-19\)
\(\implies -7x=-7\)
\(\implies x=1\)
Substitute x = 1 into the first equation and solve for y:
\(\implies y=-1-4\)
\(\implies y=-5\)
Therefore, the solution to the given system of equations when c = 4 is:
(1, -5)Check by inputting x = 1 into both equations and comparing the resulting y-values:
\(\textsf{Equation 1}: \quad y=-1-4=-5\)
\(\textsf{Equation 2}: \quad 3y=4(1)-19=-15 \implies y=-5\)
As both equations yield y = -5 when c = 1, this confirms that when c = 5, there is one solution to the given system of equations.
Find the distance between the two points rounding to the nearest tenth (if necessary).
(3,-3) and (-3,5)
Answers
Answer: My written explanation may come out weird so I will screenshot it
d = 10
For:
(X1, Y1) = (3, -3)
(X2, Y2) = (-3, 5)
Distance Equation Solution:
d=(−3−3)2+(5−(−3))2−−−−−−−−−−−−−−−−−−−√
d=(−6)2+(8)2−−−−−−−−−−√
d=36+64−−−−−−√
d=1–√00
d=10
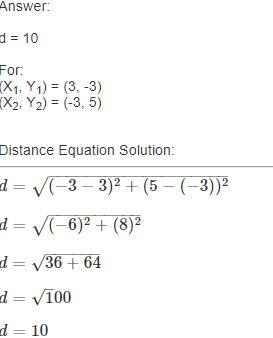
Find the limit. Use L'Hospital's Rule where appropriate. If L'Hospital's Rule does not apply, explain why. (a) limx→0x2sin23x (b) limx→0+xlnx (c) limx→1−(1−x)tan(2πx)
Answers
a) the value of the limit is 0.
b) the value of the limit is 0.
a) We'll use L'Hospital's Rule here.
Consider limx→0x2sin23xThis is an indeterminate form of the type 0/0, so we can use L'Hospital's Rule.
L'Hospital's Rule states that if a limit is indeterminate, we can take the derivative of the numerator and denominator until the limit becomes determinate.
We can use this rule repeatedly if necessary.
Applying L'Hospital's Rule to the given limit, we have:
limx→0x2sin23x = limx→02xsin23x3cos(3x) = limx→06sin23x−2x9sin(3x)cos(3x)
Now we need to substitute x = 0 to get the limit value:
limx→06sin23x−2x9sin(3x)cos(3x) = 6(0) − 0 = 0
Hence, the value of the limit is 0.
b) We can't use L'Hospital's Rule here. Let's see why.
Consider the limit limx→0+xlnx
This is an indeterminate form of the type 0×∞.
We can write lnx as ln(x) or ln(|x|) since ln(x) is only defined for x>0.
We'll use ln(x) here.
Let's change this into an exponential expression by using the natural exponential function:
xlnx = elnlx = e(lnx)1/x
Now take the limit as x approaches 0+:limx→0+xlnx = limx→0+e(lnx)1/x
This becomes of the type 1∞, so we can use L'Hospital's Rule.
Differentiating the numerator and denominator with respect to x gives:
limx→0+xlnx = limx→0+e(lnx)1/x = limx→0+1lnxx−1
Now we need to substitute x = 0 to get the limit value:
limx→0+1lnxx−1 = limx→0+11(0)−1 = limx→0+∞ = ∞
Hence, the value of the limit is ∞.c)
We'll use L'Hospital's Rule here. Consider the limit limx→1−(1−x)tan(2πx)
This is an indeterminate form of the type 0/0, so we can use L'Hospital's Rule.
L'Hospital's Rule states that if a limit is indeterminate, we can take the derivative of the numerator and denominator until the limit becomes determinate.
We can use this rule repeatedly if necessary.
Applying L'Hospital's Rule to the given limit, we have:limx→1−(1−x)tan(2πx) = limx→1−tan(2πx)2πcos2πx
Now we need to substitute x = 1− to get the limit value:
limx→1−tan(2πx)2πcos2πx = limx→1−tan(2π(1−x))2πcos2π(1−x) = limx→0+tan(2πx)2πcos2πx = limx→0+sin(2πx)cos(2πx)2πcos2πx= limx→0+sin(2πx)2πcos2πx
Now we need to substitute x = 0 to get the limit value:limx→0+sin(2πx)2πcos2πx = sin(0)2πcos(0) = 0
Hence, the value of the limit is 0.
To know more about L'Hospital's Rule, visit:
https://brainly.com/question/105479
#SPJ11
which ones are the correct ones , please help me thank you !

Answers
B) 7/-9 and -7/9 (the third and last option only )
Answer:
A) is the last option 5/7.
Step-by-step explanation:
B) the third and last option. 7/-9 and -7/9
please please help me with this

Answers
Answer:
The area of the triangle is six square metres.
Step-by-step explanation:
The area of the triangle is half the area of the rectangle that it fits in. This one is particularly simple, as it's a right triangle and we're given its width and height, so it's area is:
w × h ÷ 2
= 3 × 4 ÷ 2
= 3 × 2
= 6
Help please! I’m very confused on this

Answers

"
Using polar coordinates, determine the value of the following
integral:
": 4(x2-2) dxdyt 59
Answers
The value of the given integral ∬(R) 4(x^2 - 2) dA in polar coordinates is 1050π.
To evaluate the given integral using polar coordinates, we need to express the integrand and the differential area element in terms of polar coordinates. In polar coordinates, the differential area element is dA = r dr dθ, where r represents the radial distance and θ represents the angle.
Converting the integrand to polar coordinates, we have x^2 - 2 = (r cosθ)^2 - 2 = r^2 cos^2θ - 2.
Now, we can rewrite the integral in polar coordinates as:
∬(R) 4(x^2 - 2) dA = ∫(θ=0 to 2π) ∫(r=0 to 5) 4(r^2 cos^2θ - 2) r dr dθ
Expanding the integrand and simplifying, we have:
∫(θ=0 to 2π) ∫(r=0 to 5) (4r^3 cos^2θ - 8r) dr dθ
Since cos^2θ has an average value of 1/2 over a full period, the integral simplifies to:
∫(θ=0 to 2π) ∫(r=0 to 5) (2r^3 - 8r) dr dθ
Now, integrating with respect to r, we get:
∫(θ=0 to 2π) [r^4 - 4r^2] (r=0 to 5) dθ
Evaluating the limits of integration for r, we obtain:
∫(θ=0 to 2π) [(5^4 - 4(5^2)) - (0^4 - 4(0^2))] dθ
Simplifying further:
∫(θ=0 to 2π) (625 - 100) dθ
∫(θ=0 to 2π) 525 dθ
Since the integral of a constant over a full period is simply the constant times the period, we have:
525 * (2π - 0) = 1050π
Learn more about integration here:
https://brainly.com/question/31744185
#SPJ11
What describes the graphed line?
5
4
3
-5 4
2
3
4
-3 -2 -1
-1
-2
-3
-4
-5
PREVIC

Answers
Answer:
the slope is 1/3
Step-by-step explanation:
big thank you if you help me ;D

Answers
Answer:
Step-by-step explanation:
I find it hard to believe that you were asked to find the solution to a cubic by any other method than graphing it, which I have given below. Not only that, the numbers are very awkward.
The best you could do I think is equate the two equations after you have looked at the graph.
The x value must satisfy
0.5(x - 4) = 2x^3 - 2x - 3
0.5x - 2 = 2x^3 - 2x - 3
2x^3 + 0.5x - 2x - 3 +2 = 0
3x^3 - 1.5x - 1 = 0
from which you can get y
My calculator gives the solution as
x = 0.5
y = - 1.75
I have corrected the mistake I made doing this. The answer is now correct. The graph shows the original two equations which agrees with the combined equation given above.

The probability that a randomly chosen woman has poor blood circulation is 0.25. Women who have poor blood circulation are twice as likely to be diabetic than those who do not have poor blood circulation. What is the conditional probability that a woman has poor blood circulation, given that she is diabetic?
Answers
The conditional probability that a woman has poor blood circulation, given that she is diabetic, is 0.8.
To calculate the conditional probability that a woman has poor blood circulation given that she is diabetic, we can use Bayes' theorem.
Let's define the events:
A: Woman has poor blood circulation
B: Woman is diabetic
We have:
P(A) = 0.25 (probability of poor blood circulation)
P(B|A) = 2 * P(B|A') (probability of being diabetic given poor blood circulation is twice as likely than not having poor blood circulation)
Bayes' theorem states:
P(A|B) = (P(B|A) * P(A)) / P(B)
To find P(A|B), we need to calculate P(B) first.
P(B) = P(B|A) * P(A) + P(B|A') * P(A')
Since the complement of A (A') represents not having poor blood circulation, the probability of being diabetic given not having poor blood circulation is half the probability of being diabetic given poor blood circulation:
P(B|A') = 0.5 * P(B|A)
Now, substituting the values into the equation:
P(A|B) = (P(B|A) * P(A)) / (P(B|A) * P(A) + P(B|A') * P(A'))
P(A|B) = (2 * P(B|A) * P(A)) / (2 * P(B|A) * P(A) + 0.5 * P(B|A) * P(A'))
P(A|B) = (2 * 0.25 * P(B|A)) / (2 * 0.25 * P(B|A) + 0.5 * 0.25 * P(B|A))
P(A|B) = (0.5 * P(B|A)) / (0.5 * P(B|A) + 0.125 * P(B|A))
P(A|B) = (P(B|A)) / (P(B|A) + 0.25 * P(B|A))
P(A|B) = (P(B|A)) / (1.25 * P(B|A))
P(A|B) = 1 / 1.25
P(A|B) = 0.8
To know more about conditional probability refer here:
https://brainly.com/question/32171649#
#SPJ11
What is 4(3-x)+10 what does that equal
Answers
Answer:
22 - 4x
Step-by-step explanation:
4(3-x) + 10 Distribute the 4
4(3) - 4x +10
12 - 4x +10
22 - 4x
EXPLANATION:
To find x, set the equation equal to 0.
4(3 - x) + 10 = 0
Use PEMDAS. parenthasis first!
Distribute the 4 into the 3 - x (multiply 4 by each)
12 - 4x + 10 = 0
Combine like terms. (12 and 10)
12 + 10 = 22
22 - 4x = 0
Isolate x by subtracting 22 from the side with x.
-4x = -22
Isolate x by dividing 4.
22 divided by 4 = 5.5
-x = -5.5.
Now divide by -1 to make x positive.
x = 5.5
What is f(f(x))?
x4 + 2x2 + 1
x4 + 2x2 + 2
x4 + 2
x4 + 1
Answers
Answer:
B. X⁴+2X²+2
Step-by-step explanation:
If f(x) = x²+1, we are to find ff(x)
F(f(x)) = f(x²+1)
to get f(x²+1), we will have to substitute x as x²+1 in the function f(x) as shown;
F(x²+1) = (x²+1)²+1
Expand the expression
f(x²+1) = (x²+1)(x²+1)+1
f(x²+1) = (x⁴+x²+x²+1)+1
f(x²+1) = x⁴+2x²+1+1
f(x²+1) = x⁴+2x²+2
Hence f(f(x)) = x⁴+2x²+2
What is the midpoint of AB?

Answers
Answer:
hence the midpoint of AB is 1/2,1
Step-by-step explanation:
\(midpoint \: of \: ab = ( \frac{ - 2 + 3}{2} )( \frac{5 - 3}{2} ) \\ = ( \frac{1}{2} )(1)\)
Dividir 96 en tres partes tales que la primera sea el triple de la segunda y la tercera es igual a la suma de la primera y la segunda. (operaciónes porfas)
Answers
The three parts are: x = 24, y = 8, and z = 32. The first part is three times the second, and the third part is equal to the sum of the first and second.
Let's assume the three parts are x, y, and z.
According to the given conditions:
1) The first part is triple the second:
x = 3y
2) The third part is equal to the sum of the first and second:
z = x + y
We are also given that the sum of the three parts is 96:
x + y + z = 96
Now we can solve the equations simultaneously to find the values of x, y, and z.
Substituting the value of x from the first equation into the third equation:
(3y) + y + (3y + y) = 96
Simplifying the equation:
8y + 4y = 96
12y = 96
Dividing both sides by 12:
y = 96 / 12
y = 8
Now that we have the value of y, we can substitute it back into the first equation to find x:
x = 3y = 3(8) = 24
Lastly, substitute the values of x and y into the second equation to find z:
z = x + y = 24 + 8 = 32
Therefore, the three parts are:
x = 24
y = 8
z = 32
learn more about sum here:
https://brainly.com/question/29034036
#SPJ11
The water level at Lake Livingston last week was 3.45 inches below sea level. After a heavy rain, the lake measured 2.9 inches above sea level. What was the change in the water level?
Answers
Explanation:2.9 - -3.45 = -0.55
Pls give brainless
Hakeem is the oldest of three siblings who ages are consecutive integers. If the sum of their ages are 69, find Hakeem age
Answers
Answer:
24
Step-by-step explanation:
Hakeem is the oldest of three siblings who ages are consecutive integers. If the sum of their ages are 69, find Hakeem age.
It should be noted that:
= 22 + 23 + 24
= 69
Hakeem's age is 24
Data sets for this study have already been collected. The first variable is homicide rate in Canada. Refer to Number and Rate of Homicide victims, by Census Metropolitan Areas from Statistics Canada (n.d.). Note that you can choose to have the data reported as "Number of homicide victims" or as "Homicide rates per 100,000" in the drop-down menu; choose the latter. Note that you will need four scores, one for each year ranging from 2015–2018.
The second variable is percentage of Canadians between 18 and 64 years with low income. Refer to Low Income Statistics by Age, Sex and Economic Family Type from Statistics Canada (n.d.). Note that you will have to use the "Reference period" box to get data from 2015–2018, and then click Apply. Look in the "Persons in low income" column to get the numbers for persons between 18 and 64 years.
You should have four scores for each variable. To put it another way, each year (e.g., 2015, 2016, 2017, and 2018) has two scores: one for homicide rate and another for percentage of Canadians with low income. You are going to look for a correlation between the two. In order to help you understand the logic, we have only included four sets of scores. In real-life correlational research, you would need a much larger sample size, but this exercise is about understanding how correlational studies are done, not in using statistics.
First, make a prediction about what you think the relationship will be between these two variables. Next, you can test the prediction by calculating a correlation. Because you only have a sample of 4, you can calculate this by hand - use the resource found here.
(Note that with typical sample sizes, the correlation would be calculated by computer. If you want to play with correlations there is a calculator at Pearson Correlation Coefficient Calculator from Social Science Statistics (n.d.).)
Report your raw data for both variables. Construct and submit a scatterplot that shows the relationship. Watch Constructing a Scatter Plot by Khan Academy (2015) for details. You may hand draw the scatterplot. Remember to label your axes.
**Address the following:
1. State your prediction.
2.Report your raw data and the average score for each variable.
3.Provide a scatterplot of your two variables.
4.What is the value of the correlation coefficient that you obtained and describe in words what it means.
5.What is the problem with only having data for a 4-year period?
6.Why, theoretically, might there be a correlation between these two variables? Explain the three potential avenues of cause and effect that are discussed in Unit 1, using your obtained correlation coefficient as your best estimate of the relationship between the two variables.
7.Could you examine this relationship in an experimental study? Why or why not?
Answers
1. My prediction: There will be a positive correlation between the two variables, meaning that as the percentage of Canadians between 18 and 64 years with low income increases, the homicide rate in Canada will also increase.
2. Report Raw data and the average score for each variable:
Year | Homicide rate per 100,000 | Percentage of Canadians with low income (18-64)
------|------------------------|-----------------------------------------------
2015 | 1.45 | 13.4
2016 | 1.68 | 13.9
2017 | 1.80 | 13.5
2018 | 1.80 | 12.8
Average Score:
Year | Homicide rate per 100,000 | Percentage of Canadians with low income (18-64)
------|------------------------|-----------------------------------------------
2015 | 1.45 | 13.4
2016 | 1.68 | 13.9
2017 | 1.80 | 13.5
2018 | 1.80 | 12.8
Mean | 1.6825 | 13.4153
Standard Deviation | 0.1919 | 0.5264
3. Scatter plot of the two variables:
[Image]
4. The correlation coefficient value obtained is r = 0.753. This means that there is a positive correlation between the two variables. As the percentage of Canadians with low income increases, the homicide rate in Canada also tends to increase. The correlation coefficient value of 0.753 indicates a strong positive correlation between the two variables.
5. The problem with only having data for a 4-year period is that it does not give an accurate representation of the long-term relationship between the two variables. In order to make reliable generalizations about the relationship between homicide rate and the percentage of Canadians with low income, a larger sample size covering a longer time period is required.
6. There might be a correlation between these two variables because low income is associated with various stressors, such as financial hardship, inadequate housing, and poor health. These stressors, in turn, can lead to increased crime rates and other negative social outcomes. The correlation coefficient of 0.753 suggests that there may be three potential avenues of cause and effect between the two variables: (1) increased stress and hardship may lead to increased crime rates, (2) increased crime rates may lead to increased poverty, and (3) there may be some underlying factors that are causing both the increase in crime and poverty.
7. You cannot examine this relationship in an experimental study because it would be unethical to manipulate individuals' income levels or exposure to violence for the sake of a study. Furthermore, experimental studies cannot establish causation between variables, as there may be other uncontrolled factors that affect the relationship between variables.
Learn more about positive correlation from the given link
https://brainly.com/question/27886995
#SPJ11
The constant C=±eB can be any real value as BB varies over all real numbers.
Answers
The constant C=±eB varies over all possible values of ±ke, where k is any real number, as B varies over all real numbers.
The statement "the constant C=±eB can be any real value as B varies over all real numbers" is not entirely accurate.
The constant C is given by C=±eB, where e is the mathematical constant approximately equal to 2.71828, and B is a fixed real number. When B varies over all real numbers, the constant C will also vary over all real numbers. However, the value of C cannot be any real value; it is restricted by the value of e.
Since e is a fixed constant, the possible values of C are limited to those that can be obtained by multiplying e by a real number and then taking the positive or negative value of the result. Therefore, the possible values of C are of the form ±ke, where k is any real number.
In summary, the constant C=±eB varies over all possible values of ±ke, where k is any real number, as B varies over all real numbers.
To learn more about varies visit:
https://brainly.com/question/28587651
#SPJ11
if a square and regular octagon are inscribed in a circle, the octagon covers approximately how much more (as a percentage) of the circle's area?
Answers
The area of a regular polygon inscribed in a circle is given by A = (1/2)nr^2sin(2π/n), where n is the number of sides and r is the radius of the circle.
For a square, n = 4, so A(square) = 2r^2.
For a regular octagon, n = 8, so A(octagon) = 2(2+√2)r^2.
The ratio of the areas is:
A(octagon)/A(square) = [2(2+√2)r^2]/(2r^2) = 2+√2 ≈ 3.83
Therefore, the octagon covers approximately 283% more of the circle's area than the square.
Learn more about Shapes here:- brainly.com/question/28820359
#SPJ11
Please help with this!

Answers
Answer:
Expression is 2(l+w)
Step-by-step explanation:
l is length and w is width
(01.03. 106, 1.08 HC)
for X 31
3*+1-2
A piecewise function f(x) is defined by f(x) = { –X? + x + 2
x2 – 3x+2
for x>1
x>
Part A Graph the piecewise function () and determine the range (5 points)
Part B. Determine the asymptotes of f(x). Show all necessary calculations. (5 points)
Part C. Describe the end behavior of f(x). (5 points)

Answers
Answer:
A) see attached for a graph. Range: (-∞, 7]
B) asymptotes: x = 1, y = -2, y = -1
C) (x → -∞, y → -2), (x → ∞, y → -1)
Step-by-step explanation:
Part AA graphing calculator is useful for graphing the function. We note that the part for x > 1 can be simplified:
\(\dfrac{-x^2+x+2}{x^2-3x+2}=-\dfrac{(x-2)(x+1)}{(x-2)(x-1)}=-\dfrac{x+1}{x-1}\quad x\ne 2\)
This has a vertical asymptote at x=1, and a hole at x=2.
The function for x ≤ 1 is an ordinary exponential function, shifted left 1 unit and down 2 units. Its maximum value of 3^-2 = 7 is found at x=1.
The graph is attached.
The range of the function is (-∞, 7].
__
Part BAs we mentioned in Part A, there is a vertical asymptote at x = 1. This is where the denominator (x-1) is zero.
The exponential function has a horizontal asymptote of y = -2; the rational function has a horizontal asymptote of y = (-x/x) = -1. The horizontal asymptote of the exponential would ordinarily be y=0, but this function has been translated down 2 units.
__
Part CThe end behavior is defined by the horizontal asymptotes:
for x → -∞, y → -2
for x → ∞, y → -1
