What are the domain and range of the function f(x)=3x-1 /2
Answers
Answer:
f(x)=3x−1
2
Step-by-step explanation:
The domain of the expression is all real numbers except where the expression is undefined. In this case, there is no real number that makes the expression undefined. The range is the set of all valid y values. The domain of the expression is all real numbers except where the expression is undefined. In this case, there is no real number that makes the expression undefined.
Interval Notation:
(-∞,∞)
Set-Builder Notation:
{x|x∈R}
The range is the set of all valid
y
values. Use the graph to find the range.
Interval Notation:
(−∞,∞)
Set-Builder Notation:
{y|y∈R}
Determine the domain and range.
Domain:
(−∞,∞),{x|∈R}
Range:
(−∞,∞),{y|y∈R}
Related Questions
Can someone help me find X and the measure of TS? Pleaseee

Answers
Given:
QR=20, TS=4x-3, RS=16.
To find:
The value of x and TS.
Solution:
In the figure QR is tangent and RT is secant to the given circle.
According to the secant-tangent theorem, the square of the length of the tangent segment is equal to the product of the lengths of the secant and its external segment, if the tangent and secant are drawn to a from the an external point.
Using secant-tangent theorem, we get
\(QR^2=RS\times RT\)
\(QR^2=RS\times (TS+RS)\)
\(20^2=16\times (4x-3+16)\)
\(400=16\times (4x+13)\)
Divide both sides by 16.
\(25=4x+13\)
Subtracting both sides by 13.
\(25-13=4x\)
\(12=4x\)
Divide both sides by 4.
\(3=x\)
Now,
\(TS=4x-3\)
\(TS=4(3)-3\)
\(TS=12-3\)
\(TS=9\)
Therefore, the value of x is 3 and the measure of TS is 9 units.
Find each value given the following function:

Answers
Answer:
Step-by-step explanation:
1) f(-4) --> if x < or equal to 3
2) 1/(-4)-4
3) The answer is - 1/8
Write a system of linear inequalities represented by the graph.

Answers
The inequalities representing the graph are y ≥ - 3x + 2 and y ≥ (2/3)x - 1.
What are inequalities and their types?Inequality is a relation that compares two numbers or other mathematical expressions in an unequal way.
The symbol a < b indicates that a is smaller than b.
When a > b is used, it indicates that a is bigger than b.
a is less than or equal to b when a notation like a ≤ b.
a is bigger or equal value of an is indicated by the notation a ≥ b.
First, we have to determine the two lines.
Line₁.
(0, 2) and (1, - 1).
m = (- 1 - 2)/(1 - 0).
m = - 3.
- 1 = - 3(1) + b.
b = 2.
y = - 3x + 2.
Line₂.
(0, - 2) and (3, 0).
m = (0 + 2)/(3 - 0).
m = 2/3.
0 = (2/3)(3) + b.
b = - 1.
y = (2/3)x - 1.
So, The two inequalities are y ≥ - 3x + 2 and y ≥ (2/3)x - 1.
learn more about inequalities here :
https://brainly.com/question/28823603
#SPJ1
(08.03|08.04 HC)
For the regions A and B shown in the graph:
Part A: Discuss the limits of integration. (3 points)
Part B: Set up an integral expression that represents the total area. (4 points)
Part C: Calculate the total area. (3 points)

Answers
The total area from the graph is 2.737.
What is area?Area is the amount of space occupied by a two-dimensional figure. In other words, it is the quantity that measures the number of unit squares that cover the surface of a closed figure. The standard unit of area is square units which is generally represented as square inches, square feet, etc.
First of all, lets calculate the points of intersection (P, Q, R)
x²+3=(x+2) +5
x²-2=√(x+2)
x⁴+4-4x²=x+2
x⁴-4x²-x+2=0
(x-2)(x³+2x²-1)=0
(x-2)(x+1)(x²+x-1)=0
x=2, -1, -1±√(1+4)/2
Clearly, the x-coordinate of Q is -1, P is -1-√5/2, R is -1+√5/2, S is 2
So the limit of integration will be
P( (-1-√5)/2, (-1-√5/2)² +3)=P((-1-√5)/2, (3+√5/2))
Q(-1, (-1)²+3)=Q(-1, 4)
Area A:
\(\int\limits^\frac{3+\sqrt{5} }{2} _4 {-\sqrt{-y-3}-((y-5)^2 -2)} \, dx\)
= \([\frac{-(y-3)^\frac{3}{2} }{\frac{3}{2} }-\frac{(y-5)^3}{3}+3y]^{\frac{3+\sqrt{5} }{2} }_4\)
= 2.07
Area B:
\(\int\limits^\frac{-1+\sqrt{5} }{2} _4 {-\sqrt{x+2}+5-(x^2+3)} \, dx\)
= \([\frac{-(x+2)^\frac{3}{2} }{\frac{3}{2} }+5x-\frac{x^3}{3}-3x]^{\frac{-1+\sqrt{5} }{2} }_{-1}\)
= 0.667
Total area = 2.07+0.667
= 2.737
Therefore, the total area from the graph is 2.737.
Learn more about the area here:
https://brainly.com/question/27683633.
#SPJ1
How factorize this : ( + )( – ) + (– + )( – )
Answers
Answer:
this very easy to factorize this because (-+)is- (+-)-
(++)+ (--)+ but the sign which is bigger we have to keep that
11
12
10
7
8
6
5
29 and 22
23 and 22
26 and 23
21 and 27
Submit
Work it out

Answers
Answer: Angle 3 and Angle 2
Step-by-step explanation:
The angles form a linear pair, which means they are supplementary.
Calc II Question
Find the volume of the solid obtained by rotating the region bonded bt the given curves about the specified line.
Y = e^-x
Y = 1
X = 2
About the Y = 2
Answers
Answer:
\(\displaystyle \frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Step-by-step explanation:
This can be solved with either the washer (easier) or the shell method (harder). For the disk/washer method, the slice is perpendicular to the axis of revolution, whereas, for the shell method, the slice is parallel to the axis of revolution. I'll show how to do it with both:
Shell Method (Horizontal Axis)
\(\displaystyle V=2\pi\int^d_cr(y)h(y)\,dy\)
Radius: \(r(y)=2-y\) (distance from y=2 to x-axis)
Height: \(h(y)=2-(-\ln y)=2+\ln y\) (\(y=e^{-x}\) is the same as \(x=-\ln y\))
Bounds: \([c,d]=[e^{-2},1]\) (plugging x-bounds in gets you this)
Plugging in our integral, we get:
\(\displaystyle V=2\pi\int^1_{e^{-2}}(2-y)(2+\ln y)\,dy=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Washer Method (Parallel to x-axis)
\(\displaystyle V=\pi\int^b_a\biggr(R(x)^2-r(x)^2\biggr)\,dx\)
Outer Radius: \(R(x)=2-e^{-x}\) (distance between \(y=2\) and \(y=e^{-x}\))
Inner Radius: \(r(x)=2-1=1\) (distance between \(y=2\) and \(y=1\))
Bounds: \([a,b]=[0,2]\)
Plugging in our integral, we get:
\(\displaystyle V=\pi\int^2_0\biggr((2-e^{-x})^2-1^2\biggr)\,dx\\\\V=\pi\int^2_0\biggr((4-4e^{-x}+e^{-2x})-1\biggr)\,dx\\\\V=\pi\int^2_0(3-4e^{-x}+e^{-2x})\,dx\\\\V=\pi\biggr(3x+4e^{-x}-\frac{1}{2}e^{-2x}\biggr)\biggr|^2_0\\\\V=\pi\biggr[\biggr(3(2)+4e^{-2}-\frac{1}{2}e^{-2(2)}\biggr)-\biggr(3(0)+4e^{-0}-\frac{1}{2}e^{-2(0)}\biggr)\biggr]\\\\V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\biggr(4-\frac{1}{2}\biggr)\biggr]\)
\(\displaystyle V=\pi\biggr[\biggr(6+4e^{-2}-\frac{1}{2}e^{-4}\biggr)-\frac{7}{2}\biggr]\\\\V=\pi\biggr(\frac{5}{2}+4e^{-2}-\frac{1}{2}e^{-4}\biggr)\\\\V=\pi\biggr(\frac{5}{2}+\frac{4}{e^2}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4}{2e^4}+\frac{8e^2}{2e^4}-\frac{1}{2e^4}\biggr)\\\\V=\pi\biggr(\frac{5e^4+8e^2-1}{2e^4}\biggr)\\\\V=\frac{\pi(5e^4+8e^2-1)}{2e^4}\approx9.526\)
Use your best judgment when deciding on what method you use when visualizing the solid, but I hope this helped!

A figure is rotated 90° clockwise about the origin. Which statement is true
about the rotated figure?
A. It is the same shape as the figure but is smaller.
B. It is the same shape and size as the figure.
OC. It is the same shape as the figure but is larger.
D. It is a different shape and size from the figure.
SUBMIT

Answers
Answer:
B.
Step-by-step explanation:
A figure rotated 90° CW about the origin will be the same size and shape as the original. Any figure rotated by any angle will be the same size and shape as the original.
Resuelve (10x-8y)(6x+4)=
Answers
Answer:
60x^2 + 40x - 48xy - 32y
Step-by-step explanation:
Let's solve this using the FOIL (first, inner, outer, last) method.
(10x-8y) (6x+4)
= 10x × 6x + 10x × 4 - 8y × 6x - 8y × 4
= 60x^2 + 40x - 48xy - 32y
Answer: 60x^2 + 40x - 48xy - 32y
Soory for the wrong answer i re solved it :)
Determine which set of side measurements could be used to form a triangle.
a. 12, 23, 7
b. 10, 7, 2
c. 8, 3, 11
d. 5, 11, 8
Answers
The sets of side measurements that can form a triangle are: c. 8, 3, 11
d. 5, 11, 8
To determine which set of side measurements could be used to form a triangle, we need to apply the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Let's evaluate each set of side measurements:
a. 12, 23, 7
In this case, the sum of the lengths of the two shorter sides (12 and 7) is 19, which is less than the length of the longest side (23). Therefore, this set of side measurements cannot form a triangle.
b. 10, 7, 2
Here, the sum of the two shorter sides (10 and 2) is 12, which is greater than the length of the longest side (7). This set of side measurements also fails to satisfy the triangle inequality theorem and cannot form a triangle.
c. 8, 3, 11
The sum of the two shorter sides (8 and 3) is 11, which is greater than the length of the longest side (11). Therefore, this set of side measurements can form a triangle.
d. 5, 11, 8
In this case, the sum of the lengths of the two shorter sides (5 and 8) is 13, which is greater than the length of the longest side (11). Hence, this set of side measurements can also form a triangle.
In summary, the sets of side measurements that can form a triangle are:
c. 8, 3, 11
d. 5, 11, 8
For more such questions on measurements visit:
https://brainly.com/question/25770607
#SPJ8
Drag the tiles to the correct boxes to complete the pairs not all tiles will be used.

Answers
Answer:
I will answer them from top to bottom
1. 2A
2. 2A-B
3. 2A+3A
4. 2(A-B)
Step-by-step explanation:
You don't need an explanation. I am just putting this here so my answer does not get taken down.
Please help me with this

Answers
Answer:
z = 99
Step-by-step explanation:
\(\frac{z}{9}\) + 4 = 15 ( subtract 4 from both sides )
\(\frac{z}{9}\) = 11 ( multiply both sides by 9 to clear the fraction )
z = 99
y=9/4×2
sketch the graph of f and f on the same set of axes
Answers
The graph of the function \(f(x) = (9/4)x^2\) is a symmetric upward-opening parabola.
The graph represents a parabola that opens upward. As x increases, the corresponding y-values increase, forming a curved shape. The vertex of the parabola is at the origin (0,0). The graph is symmetric with respect to the y-axis, meaning that the left and right sides of the parabola are mirror images of each other.The slope of the graph gradually increases as x moves away from the origin. The steepness of the curve becomes more pronounced, indicating a faster rate of increase in y-values for larger x-values.The graph does not intersect the x-axis, indicating that there are no real roots or solutions for the equation f(x) = 0. The y-intercept of the graph is at (0, 0), and the y-values increase indefinitely as x approaches positive or negative infinity.Overall, the graph represents a quadratic function with a positive leading coefficient, resulting in an upward-opening parabolic curve. The graph has been attached.
For more questions on graph:
https://brainly.com/question/19040584
#SPJ8

How are the two angles related?

Answers
The two angles are related in that they are supplementary angles
Supplementary angles would add tuo to 180 degrees according to the angle Theorem.
Adding the two given angles :
52+128 = 180These angles are supplementary
The angles aren't vertical in that , vertical angles should have the same vertex. Complementary angles on the other hand add to 90 degrees. While the angles doesn't share the same side, hence, they aren't adjacent.
Hence, the angles are related as they are supplementary angles .
Learn more on angles : https://brainly.com/question/11955149
#SPJ1
60°
Х
48°
72°
X-
degrees

Answers
Answer:
x=132
Step-by-step explanation:
Hey There!
The angle that is equal to 48 and angle x are supplementary angles meaning that they will add up to equal 180
so to find x we subtract 48 from 180
180-48=132
therefore x=132
The value of x will be;
⇒ x = 132°
What is mean by Triangle?A triangle is a three sided polygon, which has three vertices and three angles which has the sum 180 degrees.
Given that;
The triangle is shown in figure.
The interior angles are;
⇒ 60°, 72° and 48°
Now,
We know that;
The sum of two opposite interior angle of the a triangle is equal to the exterior angle of the triangle.
So, We get;
⇒ x = 60° + 72°
⇒ x = 132°
Thus, The value of x = 132°
Learn more about the triangle visit;
https://brainly.com/question/17335144
#SPJ2
Tree loaves of bread cost $2.43.how much do two loaves cost
Answers
Answer:
$1.62
Step-by-step explanation:
If you divide $2.43 by 3 it's 0.81 and that's the cost of one loaf of bread so multiply that by 2 and you get the cost of two loaves of bread which is $1.62
Which of the following is true?
a. The p-value for a one-tailed test would be the same as the current p-value.
b. The p-value for a one-tailed test would be half the current p-value.
c. If this test was one-tailed instead of two-tailed g, you would reject the null.
d. If this test was one-tailed instead of two-tailed, you would still fail to reject the null.
d. The p-value for a one-tailed test would be double the current p-value.
Answers
Answer:
The correct option is c which is if this test was one-tailed instead of two-tailed, you would reject the null.
Step-by-step explanation:
a: This statement cannot be true as the p-value for a 1 tailed test is dependent on the level of significance and other features.
b: This statement cannot be true as there is no valid mathematical correlation between the p-value of the one-tailed test and the current p-value.
c: This statement is true because due to the enhanced level of significance, the null hypothesis will not be rejected.
d: This statement is inverse of statement c which cannot be true.
e: The statement cannot be true as there is no correlation between the current p-value and the p-value of 1 tailed test. The correlation exists between the values of one-tailed and two-tailed p-values.
Use the Pythagorean Theorem to find the length of the leg in the triangle shown below. 3, 5
Answers
Step-by-step explanation:
use the pythagorean theorem to find the length of the leg in the triangle below
The following quadrilateral is a parallelogram. Solve for x, y, and z.

Answers
Answer:
Angle X = 73 degrees, Angle Z = 34 degrees, and Angle Y = 146 degrees
1. Draw a quadrilateral with 2 parallel sides. It should have 2 pairs of perpendicular lines.
Answers
Answer:
draw a rectangle
Step-by-step explanation:
a rectangle has 2 long sides and 2 short ones it has 2 sets of simailer and has 2 perpundicular
What is the simplified form of the expression below? (6 + 7b) + 14
Answers
Answer: 20+7b
Step-by-step explanation:
Given
(6+7b)+14
Take off parentheses
=6+7b+14
Move like terms together (Commutative property)
=6+14+7b
Combine like terms
=20+7b
Hope this helps!! :)
Please let me know if you have any question
Answer:
\(\huge\boxed{ answer}\)
\(\blue\star\)6 + 7b + 14 = 0
\(\blue\star\)7b + 20 = 0
\(\blue\star\)7b = - 20
\(\blue\star\)b = -20\7
\(\star\)simplified form
\(\blue\star\)(6 + 7b) +14
firstly remove the brackets.
\(\blue\star\)6 + 7b +14
seprate terms and variables
\(\blue\star\) 7b +20
\(\huge\boxed{7b + 20}\)
Hope it helps..
The Riley family has 3 children all born 1 year apart. Kate is the youngest, Bradley is the middle child, and Cameron is the oldest. Together, the children's ages total 36. How old is Kate?
Answers
Step-by-step explanation:
12
Answer:
11
Step-by-step explanation:
11+12+13 =36
So Kate would be 11. Bradley would be 12. And Cameron would be 13
A group of friends wants to go to the amusement park. They have no more than $125 to spend on parking and admission. Parking is $15, and tickets cost $12.50 per person, including tax. Write and solve an inequality which can be used to determine pp, the number of people who can go to the amusement park.
Answers
Answer:
100
Step-by-step explanation:
CF AND AH ARE SKEW PERPENDICULAR PARALLEL
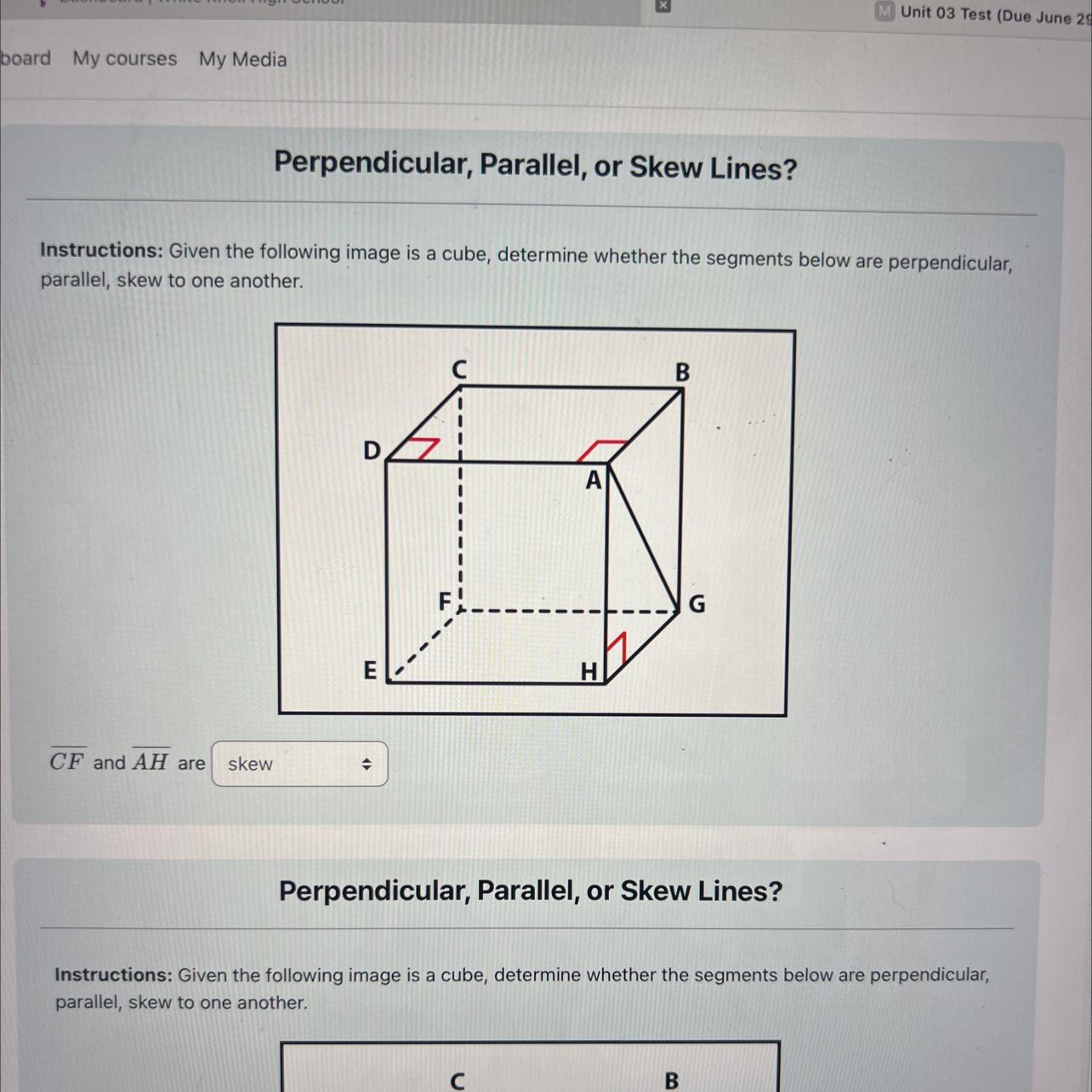
Answers
Reason: The two line segments CF and AH point in the same direction, and they never intersect. Therefore, we consider them parallel.
Skew lines are ones that point in different directions. An example of a pair of skew lines would be AB and DE. Skew lines never intersect, but we don't consider them parallel.
During a chemistry experiment, the volume of a solution increases when distilled water is added to the solution at a constant rate of 100 mL/min. Initially, there are 50 mL of solution, and water is added for 5 min.

Answers
Answer:
yes and there a r godd film?
Step-by-step explanation:
hi! Can someone please help me out? Thank you so much :) I’ll give brainly. Question is in image

Answers
Answer:
d) 189.3 in²
Step-by-step explanation:
Area of rectangle is,
→ w × l
→ 10 × 15
→ 150 in²
Area of semi circle is,
→ (1/2)πr²
→ (1/2) × 3.14 × (5)²
→ 1.57 × 25
→ 39.3 in²
Now the total area will be,
→ 150 + 39
→ 189.3 in²
Thus, total area is 189.3 in².
A bucket contains 72 red, 48 blue, 48 green, and 48 yellow crayons. The art teacher also has 120 pieces of drawing paper. What is the largest number of identical kits the art teacher can make with all of the crayons and all of the paper?
Answers
The art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper for proper distribution.
To determine the largest number of identical kits the art teacher can make using all the crayons and drawing paper, we need to find the greatest common divisor (GCD) of the quantities.
The GCD represents the largest number that can divide all the quantities without leaving a remainder.
The GCD of the quantities of crayons can be found by considering the prime factorization:
72 = 2³ × 3²
48 = 2⁴ × 3
48 = 2⁴ × 3
48 = 2⁴ × 3
The GCD of the crayons is 2³ × 3 , which is 24.
Now, we need to find the GCD of the quantity of drawing paper:
120 = 2³ × 3 × 5
The GCD of the drawing paper is also 2³ × 3 , which is 24.
Since the GCD of both the crayons and drawing paper is 24, the art teacher can make a maximum of 24 identical kits using all the crayons and drawing paper.
Each kit would contain an equal distribution of crayons and drawing paper.
Learn more about distribution here:
brainly.com/question/30034780
#SPJ1
Tonya and Emily each have an online jewelry store. Let T represent the amount of money Tonya earns daily, and let
E represent the amount of money Emily earns daily. The mean difference, D = T-E, of the amount of money that
Tonya and Emily earn on a typical day is $312. What is the correct interpretation of this value?
O On average, Tonya earns $312 daily.
O Emily is earning $312 per customer, on average.
O Tonya and Emily are each earning $312 on a typical customer.
On average, Tonya makes $312 more than Emily on a typical day.
Answers
Answer:
On average, Tonya makes $312 more than Emily on a typical day.
Step-by-step explanation:
I was just studying that question a few hours ago
Find the present value of an annuity which pays ` 200 at the end of each 3 months for 10 years assuming
money to be worth 5% converted quarterly?
(a) ` 3473.86
(b) ` 3108.60
(c) ` 6265.38
(d) None of thes
Answers
The present value of the annuity is approximately `7032.08. The correct answer is option (d) None of these.
To find the present value of an annuity, we can use the formula:
PV = PMT * (1 - (1 + r)^(-n)) / r
Where PV is the present value, PMT is the periodic payment, r is the interest rate per period, and n is the number of periods.
In this case, the periodic payment is `200, the interest rate is 5% (or 0.05) converted quarterly, and the number of periods is 10 years, which equals 40 quarters.
Plugging in these values into the formula, we get:
PV = 200 * (1 - (1 + 0.05)^(-40)) / 0.05
Simplifying the equation, we find:
PV ≈ 200 * (1 - 0.12198) / 0.05
PV ≈ 200 * 0.87802 / 0.05
PV ≈ 35160.4 / 0.05
PV ≈ 7032.08
Therefore, the present value of the annuity is approximately `7032.08.
None of the provided answer options (a), (b), or (c) match this result. The correct answer is (d) None of these.
For more such questions on annuity
https://brainly.com/question/25792915
#SPJ8
a new social media sit is increasing its user base by approximately 4% per month. If the site currently has 35.930 users, what will the approximate user base be 10 months from now?
Answers
Answer:
The approximate user base of the social media site 10 months from now would be approximately 52,374.
Step-by-step explanation:
To calculate the approximate user base of the social media site 10 months from now, considering a 4% increase per month, we can use the following steps:
1. Calculate the monthly growth factor: 1 + (4% / 100) = 1 + 0.04 = 1.04
2. Apply the growth factor to the current user base for each month:
Month 1: 35,930 * 1.04 = 37,387.2 (approx.)
Month 2: 37,387.2 * 1.04 = 38,868.49 (approx.)
...
Month 10: Previous Month * 1.04
By repeating this calculation for each month, we can determine the approximate user base 10 months from now.
Month 1: 37,387.2
Month 2: 38,868.49
Month 3: 40,391.33
Month 4: 41,957.61
Month 5: 43,569.34
Month 6: 45,228.24
Month 7: 46,936.32
Month 8: 48,695.44
Month 9: 50,507.45
Month 10: 52,374.40 (approx.)
Therefore, the approximate user base of the social media site 10 months from now would be approximately 52,374.