Wayne counts the bikes and cars in the school parking lot. There are 13 bikes and 98 cars. Which equation can be used to find t, the number of tires in the parking lot?
(13×4)+(3×t)=98
98−(13×2)=(4+t)
(13×2)+(98×4)=t
98÷(13×2)=(4×t)
Answers
The total number of tires in the parking lot, is (13×2)+(98×4)=t.
There are 13 bikes and each bike has 2 tires,
so the number of bike tires = number of bikes × number of tires
Thus, number of bike tires = 13×2.
There are 98 cars and each car has 4 tires,
so the number of car tires = number of cars × number of tires
Thus, number of car tires = 98×4.
To find the total number of tires (t),
add the number of bike tires and car tires together: (13×2)+(98×4)
Thus, t = (13×2)+(98×4)
Learn more about finding number of tires: https://brainly.com/question/1242205
#SPJ11
Related Questions
assume that A, B, and C are subsets of a universal set U. Either
prove that the statement below is true, or give a counterexample to
show that it is false. (A-B) - (C-B) = A-(BUC)
Answers
Part A: The range shown in the of pets can be determined by examining the box-and-whisker plot. However, since the plot is not provided in the question, I am unable to provide an exact answer.
As we can see statement below is ,(A-B) - (C-B) = A-(BUC) so we cannot find the correct answer.Part B: Similarly, the range of the middle 50% of the average life span of pets cannot be determined without the box-and-whisker plot.
Part C: Without the box-and-whisker plot or any specific data, it is not possible to determine which quartile has the largest spread of life spans.
The spread of life spans within each quartile can be identified by analyzing the interquartile range (IQR), but since the plot or specific data is not available, we cannot make any conclusions about the quartile with the largest spread.
Learn more about: universal set
brainly.com/question/24728032
#SPJ11
This figure shows how to create a six-pointed star from twelve equilateral triangle tiles: (SEE FIGURE ATTACHED) If each of the original tiles has a perimeter of 10 cm, what is the perimeter of the final star in cm?

Answers
Answer:
Perimeter of the final star = 40 cm²
Step-by-step Explanation:
The perimeter of the six-pointed star is the sum of the sides of the 6 equilateral triangles that form a boundary around the star.
1 triangular tiles gas a perimeter of 10cm.
Only 2 out of the 3 equal sides of each of the 6 equilateral triangles form the boundary of the final star.
Therefore, perimeter of the final star = ⅔ of the total perimeter of 6 triangular tiles
= ⅔ of (10*6)
= ⅔*60
= 2*20
Perimeter of the final star = 40 cm²
A nuclide of superscript 64 subscript 29 upper c u. absorbs a positron. which is the resulting atom?
Answers
The resulting atom when a nuclide of superscript 64 subscript 29 upper c u. absorbs a positron is; Superscript 64 subscript 30 upper Z n.
How to Calculate Positron Absorption?A positron is the anti-particle of a beta particle and it is emitted by a proton-rich nucleus.
Now, the collision of an electron and a positron yields two 0.511 MeV gamma rays because Positron gamma radiation can penetrate through inches of very hard material.
Thus, the resulting atom when a nuclide of superscript 64 subscript 29 upper c u. absorbs a positron is; Superscript 64 subscript 30 upper Z n.
Read more about Positron Absorption at; https://brainly.com/question/16516281
#SPJ1
Complete the table.
starting elevation
(feet) change
(feet) final elevation
(feet)
A +200 75 up
B +200 75 down
C +200 200 down
D +200 +25
Write an addition equation and draw a number line diagram for B. Include the starting elevation, change, and final elevation in your diagram.

Answers
Answer:
Step-by-step explanation:
Starting elevation of B = +200 feet
Change in elevation for B = 75 feet down
Final elevation of B = +200 - 75 = +125 feet
The addition equation for B can be written as:
Starting elevation + Change = Final elevation
+200 - 75 = +125
The number line diagram for B is as follows:
+------------------------+------------------------+------------------------+
A B C D
+200 +125 +225
<----- 75 ft ----->
(change in elevation)
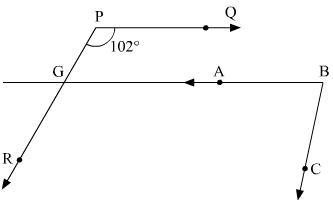
in the fig pq//ab and pr//bc if qpr= 102 degree find angle abc
Answers
The measure of the angle ABC from the diagram is equivalent to 78 degrees.
Line and anglesWe need to find <ABC
Let us produce BA to meet PR at point G.
It is given that BG || PQ
Thus, <RGB and <QPR are corresponding angles.
This shows that <RGB = <QPR since they are corresponding angles.
On the other hand, <QPR = 102 degrees and <ABC are <RGB consecutive interior angles, then:
<ABC + <RGB = 180
<ABC + 102 = 180
<ABC = 180 - 102
<ABC = 78 degrees
Hence the measure of the angle ABC from the diagram is 78 degrees.
Learn more on line and angles here: https://brainly.com/question/25770607
#SPJ1
Please help will Mark Brainily and please help me with showing work

Answers
Answer:
a=15
Step-by-step explanation:
Pythagorean Theorum says that a²+b²=c², so if we square b and c, subtract b² from c², and then square root that answer, it will equal a.
a²+8²=17²
8²=64
17²=225
225-64=225
√225=15
h(x)=−x2−6x−16 h ( x ) = − x 2 − 6 x − 16
Answers
Answer:
To analyze the function H(x) = -x^2 - 6x - 16, we can start by finding its vertex and intercepts:
Vertex: The x-coordinate of the vertex of the parabola represented by H(x) is given by x = -b/2a, where a and b are the coefficients of x^2 and x, respectively. In this case, a = -1 and b = -6, so x = -(-6)/2(-1) = 3. To find the corresponding y-coordinate, we substitute x = 3 into H(x) and get:
H(3) = -(3)^2 - 6(3) - 16 = -25
Therefore, the vertex of H(x) is (3, -25).
y-intercept: To find the y-intercept, we set x = 0 in H(x) and get:
H(0) = -(0)^2 - 6(0) - 16 = -16
Therefore, the y-intercept is (0, -16).
x-intercepts: To find the x-intercepts, we set H(x) = 0 and solve for x:
-x^2 - 6x - 16 = 0
Multiplying both sides by -1 and rearranging, we get:
x^2 + 6x + 16 = 0
Using the quadratic formula, we get:
x = (-6 ± √(6^2 - 4(1)(16))) / (2(1)) = (-6 ± 2√5i) / 2 = -3 ± √5i
Therefore, the x-intercepts are (-3 + √5i, 0) and (-3 - √5i, 0).
Axis of symmetry: The axis of symmetry is the vertical line passing through the vertex, which is x = 3 in this case.
Direction of opening: Since the coefficient of x^2 is negative, the parabola opens downwards.
Maximum value: Since the parabola opens downwards, the vertex represents the maximum point of the function. Therefore, the maximum value of H(x) is -25.
With this information, we can sketch the graph of H(x), which looks like a downward-facing parabola with vertex at (3, -25), x-intercepts at (-3 + √5i, 0) and (-3 - √5i, 0), and y-intercept at (0, -16).
The greatest value of any U.S. paper money ever printed is 10^5 dollars. What is this amount written in standard form?
Answers
Answer:
100000
Hope this helps
Use the definition of Taylor series to find the Taylor series (centered at c ) for the function. f(x)=e 4x
,c=0 f(x)=∑ n=0
[infinity]
Answers
The answer is , the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
The Taylor series expansion is a way to represent a function as an infinite sum of terms that depend on the function's derivatives.
The Taylor series of a function f(x) centered at c is given by the formula:
\(\large f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!}(x-c)^n\)
Using the definition of Taylor series to find the Taylor series (centered at c=0) for the function f(x) = e^(4x), we have:
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{e^{4(0)}}{n!}(x-0)^n\)
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n\)
Therefore, the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
The Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To find the Taylor series for the function f(x) = e^(4x) centered at c = 0, we can use the definition of the Taylor series. The general formula for the Taylor series expansion of a function f(x) centered at c is given by:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + f'''(c)(x - c)^3/3! + ...
First, let's find the derivatives of f(x) = e^(4x):
f'(x) = d/dx(e^(4x)) = 4e^(4x)
f''(x) = d^2/dx^2(e^(4x)) = 16e^(4x)
f'''(x) = d^3/dx^3(e^(4x)) = 64e^(4x)
Now, let's evaluate these derivatives at x = c = 0:
f(0) = e^(4*0) = e^0 = 1
f'(0) = 4e^(4*0) = 4e^0 = 4
f''(0) = 16e^(4*0) = 16e^0 = 16
f'''(0) = 64e^(4*0) = 64e^0 = 64
Now we can write the Taylor series expansion:
f(x) = f(0) + f'(0)(x - 0) + f''(0)(x - 0)^2/2! + f'''(0)(x - 0)^3/3! + ...
Substituting the values we found:
f(x) = 1 + 4x + 16x^2/2! + 64x^3/3! + ...
Simplifying the terms:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
Therefore, the Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To know more about Taylor series, visit:
https://brainly.com/question/32235538
#SPJ11
\(-0.2\sqrt{x^2}\) You have to simplify this
Answers
Answer:
The simplified answer to that is -0.2x.
Hope this helps and if you could mark this as brainliest. Thanks!
Answer:
-0.2x
Step-by-step explanation:
If x is negative then,
-0.2(-2) = 0.4
Matti is making moonshine in the woods behind his house. He’s
selling the moonshine in two different sized bottles: 0.5 litres
and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for
a
Answers
Based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
To solve the problem using the determinant method (Cramer's rule), we need to set up a system of equations based on the given information and then solve for the unknowns, which represent the number of 0.5 litre bottles and 0.7 litre bottles.
Let's denote the number of 0.5 litre bottles as x and the number of 0.7 litre bottles as y.
From the given information, we can set up the following equations:
Equation 1: 0.5x + 0.7y = 16.5 (total volume of moonshine)
Equation 2: 8x + 10y = 246 (total earnings from selling moonshine)
We now have a system of linear equations. To solve it using Cramer's rule, we'll find the determinants of various matrices.
Let's calculate the determinants:
D = determinant of the coefficient matrix
Dx = determinant of the matrix obtained by replacing the x column with the constants
Dy = determinant of the matrix obtained by replacing the y column with the constants
Using Cramer's rule, we can find the values of x and y:
x = Dx / D
y = Dy / D
Now, let's calculate the determinants:
D = (0.5)(10) - (0.7)(8) = -1.6
Dx = (16.5)(10) - (0.7)(246) = 150
Dy = (0.5)(246) - (16.5)(8) = -18
Finally, we can calculate the values of x and y:
x = Dx / D = 150 / (-1.6) = -93.75
y = Dy / D = -18 / (-1.6) = 11.25
However, it doesn't make sense to have negative quantities of bottles. So, we can round the values of x and y to the nearest whole number:
x ≈ -94 (rounded to -94)
y ≈ 11 (rounded to 11)
Therefore, based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
for such more question on litres
https://brainly.com/question/27877215
#SPJ8
Question
Matti is making moonshine in the woods behind his house. He’s selling the moonshine in two different sized bottles: 0.5 litres and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for a 0.7 litre bottle 10€. The last patch of moonshine was 16.5 litres, all of which Matti sold. By doing that, he earned 246 euros. How many 0.5 litre bottles and how many 0.7 litre bottles were there? Solve the problem by using the determinant method (a.k.a. Cramer’s rule).
Find the area of the following shape. Show all work

Answers
Best way to solve this is by using
\( \sqrt{s(s - a)(s - b)(s - c)} \)
\(where \: s = \frac{a + b + c}{2} \)
s=(12+8+17)/2
=18.5
using the formulae
area =43.5
Suppose you are the manager of a firm. The accounting department has provided cost estimates, and the sales department sales estimates, on a new product. Analyze the data they give you, shown below, determine what it will take to break even, and decide whether to go ahead with production of the new product. Cost is C(x) = 135x + 55, 620 and revenue is R(x) = 180x; no more than 2097 units can be sold. The break-even quantity is _____ units, which is than the number of units that can be sold, so the firm produce the product because it would money.
Answers
Answer: To determine the break-even quantity, we need to find the point where the revenue equals the cost. In other words, we need to solve the equation R(x) = C(x).
Given:
Cost function: C(x) = 135x + 55,620Revenue function: R(x) = 180xMaximum units that can be sold: 2097Setting R(x) = C(x), we have:
180x = 135x + 55,620Subtracting 135x from both sides of the equation:
180x - 135x = 55,620Simplifying the left side:
45x = 55,620Dividing both sides by 45:
x = 1,236The break-even quantity is 1,236 units.
Since the break-even quantity (1,236 units) is less than the maximum number of units that can be sold (2,097 units), the firm can produce the product because it would make money.
To determine the break-even quantity and decide whether to proceed with the production of the new product, we need to analyze the cost and revenue data provided.
The cost function is given as C(x) = 135x + 55,620, where x represents the quantity of units produced. The revenue function is given as R(x) = 180x. To break even, the total cost and total revenue should be equal. We can set up an equation based on this condition: C(x) = R(x). Substituting the given cost and revenue functions: 135x + 55,620 = 180x
To solve for x, we can subtract 135x from both sides: 55,620 = 45x. Now, divide both sides by 45: x = 1,236. The break-even quantity is 1,236 units.
Since the number of units that can be sold is no more than 2,097 units, which is greater than the break-even quantity of 1,236 units, the firm can produce the product. The break-even point indicates the minimum number of units that need to be sold to cover the costs, and since the firm can sell more than the break-even quantity, it has the potential to make a profit. However, further analysis of other factors such as market demand, competition, and potential profitability should also be considered before making a final decision.
To learn more about cost click here: brainly.com/question/14566816
#SPJ11
(1 point) standard automobile license plates in a country display 2 numbers, followed by 3 letters, followed by 2 numbers. how many different standard plates are possible in this system? (assume repetition of letters and numbers is allowed.) your answer is :
Answers
Therefore ,there are 158,184,000 ways to create a license plate in this system.
What is combination ?A selection from a group of separate items is called a combination in mathematics, and the order in which the elements are chosen is irrelevant (unlike permutations). An apple and a pear, an apple and an orange, or a pear and an orange are three combinations of two fruits that can be chosen from a set of three fruits, such as an apple, an orange, and a pear. Formally speaking, a set S's k-combination is a subset of S's k unique components. Two combinations are therefore equal if and only if they have the same elements in both combinations.
According to the counting principle, the total number of ways to obtain a license plate is calculated by multiplying the number of times each of these events might occur together.
The first number (the digits 1 through 9) can be obtained in nine different ways.
There are 26 methods to obtain the first letter. There are 26 ways to obtain the following letter (repetition is acceptable).
There are 26 methods to get the third letter, 10 ways to get the next number (zero is acceptable), and 10 ways to get the following number with repetitions.
How many ways are there to get the next number? 10 ways\s.
Thus ,total options for obtaining a license plate:
9 x 26 x 26 x 26 x 10 x 10=158184000
Therefore ,there are 158,184,000 ways to create a license plate in this system.
To know more about combination , visit
https://brainly.com/question/27058178
#SPJ4
The sum of the first ten terms of a linear sequence is 145. the sum of the next ten term is 445. find the sum of the first four term of the sequence
Answers
The sum of the first four terms of the sequence is 22.
In this question,
The formula of sum of linear sequence is
\(S_n =\frac{n}{2}(2a+(n-1)d)\)
The sum of the first ten terms of a linear sequence is 145
⇒ \(S_{10} =\frac{10}{2}(2a+(10-1)d)\)
⇒ 145 = 5 (2a+9d)
⇒ \(\frac{145}{5} =2a+9d\)
⇒ 29 = 2a + 9d ------- (1)
The sum of the next ten term is 445, so the sum of first twenty terms is
⇒ 145 + 445
⇒ \(S_{20} =\frac{20}{2}(2a+(20-1)d)\)
⇒ 590 = 10 (2a + 19d)
⇒ \(\frac{590}{10}=2a+19d\)
⇒ 59 = 2a + 19d -------- (2)
Now subtract (2) from (1),
⇒ 30 = 10d
⇒ d = \(\frac{30}{10}\)
⇒ d = 3
Substitute d in (1), we get
⇒ 29 = 2a + 9(3)
⇒ 29 = 2a + 27
⇒ 29 - 27 = 2a
⇒ 2 = 2a
⇒ a = \(\frac{2}{2}\)
⇒ a = 1
Thus, sum of first four terms is
⇒ \(S_4 =\frac{4}{2}(2(1)+(4-1)(3))\)
⇒ \(S_4 =2(2+(3)(3))\)
⇒ S₄ = 2(2+9)
⇒ S₄ = 2(11)
⇒ S₄ = 22.
Hence we can conclude that the sum of the first four terms of the sequence is 22.
Learn more about sum of sequence of n terms here
https://brainly.com/question/20385181
#SPJ4
the adult men of the dinaric alps have the highest average height of all regions. the distribution of height is approximately normal with a mean height of 6 ft 1 in (73 inches) and standard deviation of 3 inches. what percentage of men have a height between 68 and 72 inches?
Answers
Approximately 34.13% of men in the Dinaric Alps region have a height between 68 and 72 inches.
To calculate this percentage, we need to find the area under the normal distribution curve between 68 and 72 inches. We can do this by standardizing the values using the z-score formula:
z = (x - μ) / σ
where x is the height value, μ is the mean height, and σ is the standard deviation.
For x = 68 inches, the z-score is:
z = (68 - 73) / 3 = -1.67
For x = 72 inches, the z-score is:
z = (72 - 73) / 3 = -0.33
Using a standard normal distribution table or a calculator with a normal distribution function, we can find that the area under the curve between z = -1.67 and z = -0.33 is approximately 0.3413 or 34.13%. Therefore, approximately 34.13% of men in the Dinaric Alps region have a height between 68 and 72 inches.
For more questions like Deviation visit the link below:
https://brainly.com/question/26161813
#SPJ11
x + 7 - 5x - 5 simplified
Answers
Step-by-step explanation:
x + 7- 5x- 5
= x - 5x +7- 5
= -4x + 2
= -2 (2x - 1)
Answer:
-4x+2
Step-by-step explanation:
Combine Like Terms:
x + 7 - 5x - 5
-4x + 7 - 5
-4x + 2
PLEASE HELP
IM BEGGING PLEASE
Lake Pyramid, Nevada is one of the best places in the connected 48 states to
catch trophy cutthroat trout. History shows that about 37% of guest catch a
cutthroat. Let X be a random variable that represents the first trip to Lake
Pyramid on which a guest catches a cutthroat. Let X be a random variable that
represents the first trip to Lake Pyramid on which a guest catches a cutthroat.
Find the probability that it takes the fisher no more than 4 trips to catch a
cutthroat. . *
Answers
If an event occurs 0 times (out of 4, in this case) then it does not occur at least once. So we can find the probability of it not occurring and then subtract that value from 1.
So, what are the chances of it not occurring in 1 trip?
1−.37=.63
What about not occurring in 2 trips?
(1−.37)⋅(1−.37)=.63⋅.63=.3969
Now what about not occurring in 4 trips?
.63^4 = 0.15752961
We must subtract this value from 1
(recall that what we just calculated is the probability of it not occurring, so the probability of it occurring at least once is:
1−0.15752961 = .84247039
TLDR - In 4 trips the chance of a guest catching a cutthroat once in under 4 trips in 0.84.
What is
-1.5+(4.2)=-1.5+?
Answers
Answer:
-1.5 + 4.2
Step-by-step explanation:
Since there is no negative sign,the sign would change.
So it will be -1.5+4.2
A book costs $25. It goes on sale for $22. What
47 the percent of decrease?
A
14%
B
88%
C
12%
D
86%
Answers
Find the measure of ∠C F D . A. 66° B. 72° C. 108° D. 138°
Answers
The measure of CFD is 66°.
How to calculate the angle?It should be noted that vertically opposite angles are equal.
Therefore, AFE may be equal to BFD.
In this case, AFE is given as 108° while one of the other angles is given as 42°.
Therefore, the value of CFD will be:
= 102° - 42°
= 66°
The value of CFD is 66°.
Learn more angles on;
brainly.com/question/25716982
#SPJ1

Which graph shows the image being rotated 90°?
Answers
Answer:
There is no picture, my sweetheart.
Step-by-step explanation:
Can 4, 6, and 12 be the measure of the sides of a triangle?
and
Can 6, 15, and 20 be the measure of the sides of a triangle?
Answers
Answer:
yes they can
Step-by-step explanation:
Answer:
yes
Step-by-step explanation:
yes they can............
Can anyone write the quadratic of the equation in factored form?

Answers
The factored form of the quadratic equation is given as follows:
y = 3(x + 0.6667)(x - 6).
How to obtain the factored form of the quadratic equation?The quadratic equation for this problem is defined as follows:
3x² - 16x - 7 = 5.
3x² - 16x - 12 = 0.
The coefficients are given as follows:
a = 3, b = -16, c = -12.
Hence the discriminant is of:
D = (-16)² - 4(3)(-12)
D = 400.
Then the roots are of:
x = (16 - sqrt(400))/6 = -0.6667.x = (16 + sqrt(400))/6 = 6.Considering the leading coefficient of 3 and the roots, the factored form of the equation is given as follows:
y = 3(x + 0.6667)(x - 6).
More can be learned about quadratic functions at https://brainly.com/question/1214333
#SPJ1
if the cross-price elasticity of demand for two goods is 1.25, then:________
Answers
If the cross-price elasticity of demand for two goods is 1.25, then the two goods are substitutes.
Cross Price Elasticity of Demand:
The cross elasticity of demand is an economic concept that measures the response of the quantity demanded of one good to changes in the price of another good. Also known as the cross-price elasticity of demand, this measure is calculated by dividing the percentage change in quantity demanded for one good by the percentage change in price of another commodity.
\(E_X_Y\) = \(\frac{Percentage change in Quantity of X }{Percentage Change in Quantity of Y}\)
\(E_X_Y\) = ΔQ/Q ÷ ΔP/P
= ΔQ/Q × P/ΔP
= ΔQ/ΔP × P/Q
where:
Q = Quantity of good X
P = Price of good Y
Δ = Change
The cross elasticity of demand for a substitute is always positive because an increase in the price of a substitute increases the demand for one good. For example, when the price of coffee rises, the demand for tea (alternative beverage) increases as consumers switch to cheaper but alternative beverages. This is reflected in the formula for the cross-elasticity of demand, as the numerator (the percentage change in demand for tea) and the denominator (the price of coffee) represent positive increases.
Items with a coefficient of 0 are unrelated and independent products. Commodities can be weak substitutes for which both products are positive but have a low cross-elasticity of demand. This is often the case with various alternative products such as tea or coffee. Commodities that are strong substitutes have a higher cross-elasticity of demand. Consider a different brand of tea. An increase in the price of green tea from one company has a greater impact on the demand for green tea from the other company.
The cross elasticity of demand is 1.25. Positive cross elasticity means that when the price of one good changes, the quantity demanded of another good changes in the same direction. For example, when the price of one good increases, the demand for another good increases.
This indicates that the two products are fungible. When the price of a product rises, consumers will prefer the cheaper product. As a result, the demand for alternatives will increase.
Learn more about Substitute:
https://brainly.com/question/13058734
#SPJ4
How do you identify the vertical and horizontal asymptotes for rational functions?
Answers
To identify the vertical asymptotes, we have to factor the denominator. For horizontal asymptotes, we compare the degrees of the numerator and denominator.
For rational functions, there are vertical and horizontal asymptotes. To identify the vertical asymptotes, we first have to factor the denominator. After that, we should look for values that make the denominator zero. These values can be found by setting the denominator equal to zero and solving for x. The resulting x values would be the vertical asymptotes of the function.
The horizontal asymptote is the line that the function approaches as x goes towards infinity or negative infinity. For rational functions, the horizontal asymptote is found by comparing the degrees of the numerator and the denominator.
If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0. If the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is y = the ratio of the leading coefficients. If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
To know more about the vertical asymptotes visit:
https://brainly.com/question/31315562
#SPJ11
3/4 divided by 7 is ___
Answers
Answer:
the answer is 3/28
Step-by-step explanation:
The radius of a circle is 12 yards. What is the circle's area?
Answers
The point (-3,1) is moved 3 places in the negative y direction and 2 places in the positive x direction.
What are the coordinates of the new point?
Answers
Answer:
(-6, 4)
Step-by-step explanation:
Given the coordinate points (-3,1). If The point (-3,1) is moved 3 places in the negative y direction and 2 places in the positive x direction the required coordinate will be expressed ss;
X' = (-3-3, 1+3)
X = (-6, 4)
Hence the resulting coordinate will be at:(-6, 4)
The value for the missing side is

Answers
Answer:
B
Step-by-step explanation:
\(3\sqrt{5}\)