Water flows from a faucet into a bathtub at a constant rate of 7 gallons of water pouring in every 2 minutes. The bathtub is initially empty and the plug is in. If the tub can hold 50 gallons of water, how long will it take to fill the tub? A. 14.26 minutesB. 14 minutesC. 7.14 minutesD. None of the aboveI would appreciate the help
Answers
Answer:
D. None of the above (14.28 minutes)
Explanation:
If the rate is 7 gallons every 2 minutes, we can calculate the number of gallons in the tub after X minutes using the following equation:
\(G=\frac{7}{2}X\)Then, if the tub can hold 50 gallons, we can replace G by 50 as follows:
\(50=\frac{7}{2}X\)So, the number of minutes that the tub will take to fill can be found if we solve the equation for X. Then:
\(\begin{gathered} 50\cdot2=\frac{7}{2}X\cdot2 \\ 100=7X \\ \frac{100}{7}=\frac{7X}{7} \\ 14.28=X \end{gathered}\)Therefore, the correct answer is 14.28 minutes.
Related Questions
Express cos M as a fraction in simplest terms.

Answers
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies a=\sqrt{c^2 - o^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{30}\\ a=\stackrel{adjacent}{MN}\\ o=\stackrel{opposite}{18} \end{cases} \\\\\\ MN=\sqrt{ 30^2 - 18^2} \implies MN=\sqrt{ 576 }\implies MN=24 \\\\[-0.35em] ~\dotfill\\\\ \cos(M )=\cfrac{\stackrel{adjacent}{24}}{\underset{hypotenuse}{30}} \implies \cos(M)=\cfrac{4}{5}\)
Calculate the circumference of a circle with a radius of 8 inches.
Answers
To calculate the circumference of a circle, you can use the formula:
\(\displaystyle C=2\pi r\)
Where \(\displaystyle C\) represents the circumference and \(\displaystyle r\) represents the radius of the circle.
Given that the radius \(\displaystyle r\) is 8 inches, we can substitute this value into the formula:
\(\displaystyle C=2\pi (8)\)
Simplifying the expression:
\(\displaystyle C=16\pi \)
Thus, the circumference of a circle with a radius of 8 inches is \(\displaystyle 16\pi \) inches.
Note: \(\displaystyle \pi \) represents the mathematical constant pi, which is approximately equal to 3.14159.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
What is the missing term?

Answers
X - 3
These 2 variables can not combine in any ways so the only option is to make it an equation until you find the value of “X”
answer fast............

Answers
Answer:
A)7L=7000ml C)18L=18000ml
Step-by-step explanation:
Find the equation of the line with slope = 6 and passing through (-4,-22). Write your equation in the form
y = mx + b.
Answers
Answer:
y = 6x +2
Step-by-step explanation:
It is useful to start with the point-slope form of the equation for a line when you are given a point and a slope.
y -k = m(x -h) . . . . line with slope m through point (h, k)
y -(-22) = 6(x -(-4))
y +22 = 6x +24 . . . simplify
y = 6x +2 . . . . . . subtract 22
The total number of atoms represented by Cd(CH₂CICO₂)2 is:
O a) 13
Ob) 16
O c) 17
Od) 15
Oe) 14
Answers
The total number of atoms represented by Cd(CH₂CICO₂)₂ is 15.
What is addition?In addition, items are combined and counted as a single large group. The process of adding two or more numbers together is known as addition in mathematics. The terms "addends" and "sum" refer to the numbers that are added and the result of the operation, respectively.
To find the total number of atoms represented by Cd(CH₂CICO₂)₂, we need to count the number of atoms of each element in the molecule and add them up.
Cd(CH₂CICO₂)₂ contains:
1 cadmium (Cd) atom
2 carbon (C) atoms
6 hydrogen (H) atoms
4 oxygen (O) atoms
2 chlorine (Cl) atoms
Adding these up, we get:
1 + 2 + 6 + 4 + 2 = 15
Therefore, the total number of atoms represented by Cd(CH₂CICO₂)₂ is 15.
The answer is (D) 15.
To learn more about the addition;
brainly.com/question/29464370
#SPJ2
Uhm anyone????? pleaseeeeeeeeeeeeeeeeeeeeee

Answers
Answer:
$85
Step-by-step explanation:
(if you need to explain how the anwer was gotten)
34 ÷ 4 = 8.5
8.5 × 10 = 85
1) you need to find out how much she earning in 1 hour. To do that you would divide 34 by 4 which is 8.5.
2) then multiply it by 10 hours. 8.5•10=85
The answer is 85
Write an equation in the form y=mx + b of the line that is described The y-intercept is 2 and the line is perpendicular to the line whose equation is y = 6x – 3. The equation of the line is y = (Simplify your answer. Use integers or fractions for any numbers in the expression.)
Answers
Answer:
y = -1/6x + 2
Step-by-step explanation:
To find the slope of a perpendicular line, you take the opposite reciprocal
6x -> -1/6x
y = -1/6x + 2
What is the volume, in cubic in, of a rectangular prism with a height of 11in, a width of 20in, and a length of 19in?
Answers
The volume, in cubic in, of a rectangular prism is,
⇒ V = 4,180 inches³
We have to given that;
A rectangular prism has a height of 11 in, a width of 20 in, and a length of 19in.
Now, We know that;
Volume of a rectangular prism is,
V = Length x width x height
Substitute all the values, we get;
V = 11 x 20 x 19
V = 4,180 inches³
Thus, The volume, in cubic in, of a rectangular prism is,
⇒ V = 4,180 inches³
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1
Name the 3 others names for solutions of polynomial equations
Answers
Answer:
3 types of polynomials. They are monomial, binomial and trinomial.
-------------->
There can be rational, irrational and imaginary solutions. Irrational and imaginary solutions will always come in pairs. This is due to the fact that to find these types of solutions, you must use the Quadratic Formula and the \begin{align*}\pm\end{align*} sign will give two solutions.
Step-by-step explanation:
The function f(t) = t2 + 4t - 14 represents a parabola.
Part A: Rewrite the function in vertex form by completing the square. Show your
work.
Part B: Determine the vertex and indicate whether it is a maximum or a minimum on
the graph. How do you know?
Part C: Determine the axis of symmetry for f(t).
Answers
Answer:
a: \(f(t)=(t+2)^2-18\)
b: vertex: (-2, -18)
minimum
c: x = -2
Step-by-step explanation:
Completing the square is difficult to explain in words. but I'll try my best. Let me know if you need any more information.
Part A ===============
Start with the given function in this form:
\(f(x)=ax^2+bx+c\\t^2+4t-14\)
We need an additional number, d, and we'll calculate it like this:
\(d=(\frac{b}{2a})^2 \\\\d=(\frac{4}{2(1)} )^2\\d=2^2\\d=4\)
d needs to be added and subtracted at the same time. That way we do not change the value of the expression:
\(ax^2+bx+d-d+c\\\\t^2+4t+4-4-14\)
And you can separate them like this to make it easier to read:
\((t^2+4t+4) + (-4-14)\\(t^2+4t+4)-18\)
Finally, we need to factor the trinomial in the parenthesis. Because we've completed the square, it's now a perfect square trinomial. The factored form is just:
\((x+e)^2\)
where e is half of b, or the square root of c. That looks like this in our case, and you can also expand it to make sure.
\((t+2)^2\\\\(t+2)(t+2)\\t^2+2t+2t+4\\t^2+4t+4\)
Put that all together and you get the answer:
\(f(t)=(t+2)^2-18\)
Part B ===============
Vertex form is this:
\(f(x)=a(x-h)^2+k\)
where (h, k) is the vertex and a is the scale factor.
In part A, we converted the given function into vertex form. Looking at that, you can see the vertex is at (-2, -18), and the scale factor is 1. When the scale factor is positive, the parabola faces upwards. When it's negative, the parabola faces downwards.
The scale factor is a positive 1 in this case, and if you picture that in your mind, the vertex is at the very lowest point, or the minimum, of the parabola.
Part C ==============
The axis of symmetry is always on the vertex, and that is because the vertex is the exact point where the parabola changes direction from positive to negative, or negative to positive.
The vertex of this parabola is (-2, -18), so the axis of symmetry is at x = -2.
Sorry if that got too long and hard to follow, I can clarify any part of it if needed.
PLEASE HELP! I JUST NEED TO KNOW HOW YOU SOLVE THIS!!! SEE ATTACHED!!! WILL MARK YOU BRAINLIEST!!! Surface Area

Answers
The surface area of the complex solid is 530 square yards.
How to determine the surface area of a complex solid
In this problem we need to determine the surface area of the complex solid, that is, the sum of the area of all faces of the solid. The area formulas required to find the surface area is:
A = w · h
Where:
A - Area, in square yards.w - Width, in yardsh - Height, in yards.The surface area of the complex solid is:
A = 2 · (11 yd) · (3 yd) + 2 · (4 yd)² + (12 yd) · (11 yd) + (12 yd) · (3 yd) + (12 yd) · (7 yd) + 2 · (4 yd) · (12 yd) + (12 yd) · (7 yd)
A = 66 yd² + 32 yd² + 132 yd² + 36 yd² + 84 yd² + 96 yd² + 84 yd²
A = 530 yd²
To learn more on surface areas of solids: https://brainly.com/question/31126484
#SPJ1
by how much is 68,72,526 less than a crore?
Answers
Answer:
10000000 - 6872536 = 3127474
Hence 68,72,536 is 31,27,474 less than 1,00,00,000.
for each of the number lines, write an absolute value equation in the form |x-c|=d, where c and d are some numbers, to satisfy the given solution set.

Answers
An absolute value is the numerical value of a number without consideration of its sign. It can be represented graphically by a straight line known as a number line. Absolute value equations are equations that include absolute values of variables or unknown quantities. The following are examples of how to write an absolute value equation in the form |x-c|=d to fit the provided solution sets:
Example 1:
Solution set: {x|x≤-3 or x≥1}
Absolute value equation: |x-(-1)|=4
Explanation: -1 is the midpoint of the two ranges (-3 and 1) in the solution set. |x-(-1)|=|x+1| is the absolute value expression for the midpoint -1. The distance d from -1 to the solutions' furthest endpoints, 1 and -3, is four, hence the value of d in the absolute value equation is 4.
For such more question on equations
https://brainly.com/question/22688504
#SPJ11
Which system of equations does this graph represent?(1 point)
W
3 -2 -1
O y = x2 + 2
y=x +4
Oy=x2 + 3
y = -x + 2
O y=x2+4
y=-x-1
Oy=x2 - 5
y = -x -3
4
13
=1+
ви
Answers
The system of equations which this graph represent include the following:
A. y = x² + 2
y = x + 4
How to determine an equation of this line?In Geometry, the point-slope form of a straight line can be calculated by using this equation:
y - y₁ = m(x - x₁)
Where:
x and y represent the data points.m represent the slope.First, we would find the slope of this line;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (6 - 3)/(2 + 1)
Slope (m) = 3/3
Slope (m) = 1.
At data point (-1, 3) and a slope of 1, an equation for this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y - 3 = -1(x + 1)
y = -x + 4
For the quadratic equation, we have;
y = a(x - h)² + k
6 = a(-2 - 0)² + 2
4 = a4
a = 4/4
a = 1
Therefore, the required quadratic function is given by:
y = a(x - h)² + k
y = (x - 0)² + 2
y = x² + 2
Read more on point-slope here: brainly.com/question/24907633
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

I need help with this question.

Answers
6/10=12/x
Cross multiply.
6x=120
x=20
4. The fence around a circular pool is 75 ft long.
Diameter:0ft
Radius:0ft
Is it radius diameter or circumference
Answers
The resultant values are as follows:
Radius = 11.94 ft; Diameter: 23.87 ft; Circumference = 75 ft
What is the circumference?The circumference of a circle or ellipse in geometry is its perimeter.
That is, if the circle were opened up and straightened out to a line segment, the circumference would be the length of the arc.
The curve length around any closed figure is more often referred to as the perimeter.
The length of a circle's outline is referred to as its circumference, and the length of a form with straight sides is referred to as its perimeter.
So, since the fence around the circular pool is given, then it will also be the value of the circumference of the pool.
Circumference = 75 ft
Radius:
2πr = 75
r = 75/2π = 75/(2×3.14) ≈ 11.937
radius = 11.94 ft
Diameter:
2r = 2×11 ≈ 23.87 ft
Therefore, the resultant values are as follows:
Radius = 11.94 ft; Diameter: 23.87 ft; Circumference = 75 ft
Know more about the circumference here:
https://brainly.com/question/20489969
#SPJ1
Complete question:
The fence around a circular pool is 75 ft long. Find: Radius, Diameter, and Circumference.
A rectangle has an area of 18 square centimeters.
Which of the following could be the rectangle's length and width?
(Area = length x width)
Choose all answers that apply:
B
C
1 cm and 18 cm
2 cm and 9 cm
3 cm and 6 cm
4 cm and 5 cm
Answers
Answer:
1 cm and 18 cm
2 cm and 9 cm
3 cm and 6 cm
Step-by-step explanation:
We need to find the factors of 18
which are; 1,18; 2,9; 3,6
So therefore we'd pick:
1 cm and 18 cm
2 cm and 9 cm
3 cm and 6 cm
2(x-6)²
could you please explain this to me, thanks!
Answers
Answer:
expand the square
2(x-6) (x-6)
2(x(x-6)-6(x-6)
2(x²-6x-6(x-6)
2(x²-6x-6x+36)
2(x²-12x+36)
2x²-24x+72
Step-by-step explanation:
hope this helps
2/2 equal i need to know pls pls
Answers
Answer:
If you are asking what 2 divided 2 is its 1
Step-by-step explanation:
Answer:
It equals 1
Step-by-step explanation:
Because 2 divided by 2 is 1
If a function f(x) is defined as 3x2 + x + 2, what is the value of Lim h-0 f(x+h)-f(x)/h? A. 3x + 1 B. 3x + 2 C. 6x + 1 D. 6x + 2
Answers
Answer:
\( f(x+h) = 3(x+h)^2 +(x+h) +2= 3(x^2 +2xh+h^2) +x+h+2\)
\(f(x+h) = 3x^2 +6xh +3h^2 +x+h+2= 3x^2 +6xh +x+h+ 3h^2 +2\)
And replacing we got:
\( lim_{h \to 0} \frac{3x^2 +6xh +x+h+ 3h^2 +2 -3x^2 -x-2}{h}\)
And if we simplfy we got:
\( lim_{h \to 0} \frac{6xh +h+ 3h^2 }{h} =lim_{h \to 0} 6x + 1 +3h \)
And replacing we got:
\(lim_{h \to 0} 6x + 1 +3h = 6x+1\)
And the bet option would be:
C. 6x + 1
Step-by-step explanation:
We have the following function given:
\( f(x) = 3x^2 +x+2\)
And we want to find this limit:
\( lim_{h \to 0} \frac{f(x+h) -f(x)}{h}\)
We can begin finding:
\( f(x+h) = 3(x+h)^2 +(x+h) +2= 3(x^2 +2xh+h^2) +x+h+2\)
\(f(x+h) = 3x^2 +6xh +3h^2 +x+h+2= 3x^2 +6xh +x+h+ 3h^2 +2\)
And replacing we got:
\( lim_{h \to 0} \frac{3x^2 +6xh +x+h+ 3h^2 +2 -3x^2 -x-2}{h}\)
And if we simplfy we got:
\( lim_{h \to 0} \frac{6xh +h+ 3h^2 }{h} =lim_{h \to 0} 6x + 1 +3h \)
And replacing we got:
\(lim_{h \to 0} 6x + 1 +3h = 6x+1\)
And the bet option would be:
C. 6x + 1
Answer:
6x+1
Step-by-step explanation:
Plato :)
Write the slope-intercept form of the equation of the line described. through (2, -5) perpendicular to y = 1/3x -1
Answers
Answer:
y = -3x + 1
Step-by-step explanation:
Perpendicular lines have opposite reciprocal slopes, so the slope will be -3.
Plug in the slope and given point into y = mx + b
y = mx + b
-5 = -3(2) + b
-5 = -6 + b
1 = b
Then, plug in the slope and y intercept into y = mx + b again:
y = -3x + 1 will be the equation of the line
A cabinetmaker is asked to build a cabinet with dimensions of 8 inches wide by 14 inches long by 40 inches tall. He is then asked to reduce the size of the cabinet by a scale factor of 3/4. What are the new dimensions of the cabinet?
Answers
Answer:
6 inches by 10 1/2 inches by 30 inches
Step-by-step explanation: To find this answer you have to multiply the old dimensions by the scale factor which is 3/4. You would do 8 times 3/4 which is 6 inches. Then 14 inches times 3/4 which is 10 1/2. And then 40 inches times 3/4 and that answer is 30 inches. Those are the new dimensions for the cabinet.
Julia's Burger Place made 3 burgers with onions and 12 burgers without onions. What is the ratio of the number of burgers without onions to the number of burgers with onions?
Answers
The ratio of number of burgers without onions to the number of burgers with onions is 4:1.
Ratio of numbers.The ratio of numbers implies the relationship between the numbers when expressed in its simplest fraction. The relationship can be written in form of a/ b or a:b.
Given in the question that Julia's Burger Place made 3 burgers with onions and 12 burgers without onions. Then the ratio required can be expressed as;
ratio of number of burgers without onions to burgers with onions = (number of burgers without onions)/ (number of burgers with onions)
= 12/ 3
= 4/ 1
The ratio of number of burgers without onions to burgers with onions = 4:1
Therefore, the ratio of the number of burgers without onions to the number of burgers with onions is 4:1.
Learn more about ratio of numbers at https://brainly.com/question/2914376
#SPJ1
Samantha is training for a race. The distances of her training runs form an arithmetic sequence. She runs 1 mi the first day and 2 mi the seventh day.
a. What is the explicit definition for this sequence?
b. How far does she run on day 19?
Answers
A spinner is divided into three sections: red, blue, and green. The red section is 2/5 of the area of the spinner. The blue section is 1/2 of the area of the spinner. Give the probability for each outcome. Express your answers as fractions.
Answers
Probability of red = \(\frac{4}{10}\) , blue = \(\frac{5}{10}\) , green = \(\frac{1}{10}\).
Meaning of probability :
Probability is calculation of how likely some event will happen. Whenever we are not sure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are going to happen.
The analysis of events governed by probability is called statistics.
According to the given information :
Red section = \(\frac{2}{5}\)
multiply numerator and denominator by \(2\) we get
Red section = \(\frac{4}{10}\)
Blue section = \(\frac{1}{2}\)
multiply numerator and denominator by \(5\) we get
Blue section = \(\frac{5}{10}\)
Green section = \(1\)- Red section - Blue section
Green section =\(1-\frac{4}{10} -\frac{5}{10}\)
Green section = \(\frac{1}{10}\)
Therefore Probability of red = \(\frac{4}{10}\) , blue = \(\frac{5}{10}\) , green = \(\frac{1}{10}\).
Learn more about Probability
https://brainly.com/question/11234923
#SPJ1
Write an equation for the graph below in terms of x
Y=
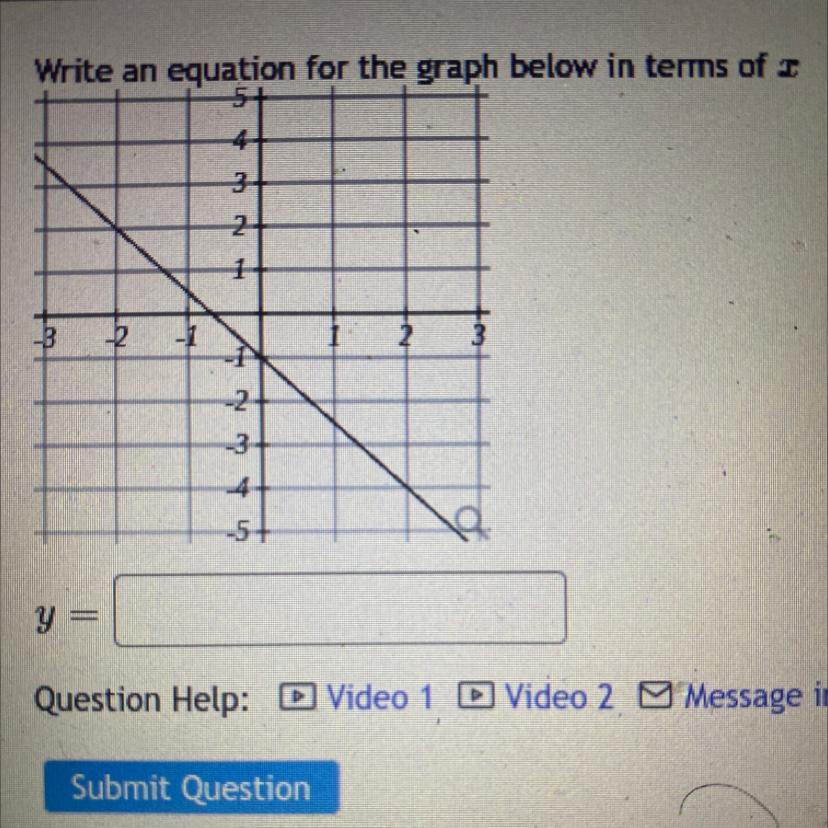
Answers
Because the slope is rise 3 run 2 and the y-intercept is -1
Martha went to a restaurant with some friends. The three of them split a large pizza. Martha then ordered a large soda for $5. Martha spent a total of $11. How much was the large pizza? (pls!!!!)
Answers
Answer:
$6
Step-by-step explanation:
there was 11 total and 5 went into the soda and 6 went into the pizza so it's 6.
Given figure below as well as the fact that a is parallel to b what is the value of x?

Answers
Answer:
17
Step-by-step explanation:
The value of x from the angles between given parallel line is 17.
What are consecutive angles in between two parallel lines?Consecutive angles lie along the transversal, both angles will always be on one side of the transversal, and they'll either both be inside the parallel lines or outside the parallel lines (interior or exterior angles, respectively). Consecutive angles are always supplementary if the transversal crosses parallel lines.
From the given figure, we have two angles 2x+5 and 8x+5.
As we know, sum of consecutive angles is 180°
Now, 2x+5+8x+5=180
10x+10=180
10x=170
x=17
So, 2x+5=39° and 8x+5=141°
Therefore, the value of x from the angles between given parallel line is 17.
Learn more about the parallel line angles here:
https://brainly.com/question/17237586.
#SPJ2
What is the percent of 1 - 3√(5/35) ?
Answers
Answer:
1 - 3√(5/35) = 1 - 3√(1/7) = 1 - 3*(1/sqrt(7)) ≈ 0.0755
0.0755 * 100 = 7.55%
Step-by-step explanation:
To find the percentage of 1 - 3√(5/35), we need to first evaluate the expression.
1 - 3√(5/35) = 1 - 3√(1/7) = 1 - 3*(1/sqrt(7)) ≈ 0.0755
To convert this decimal to a percentage, we simply multiply by 100:
0.0755 * 100 = 7.55%