water flows from a faucet at a constant rate. Kian measures 8 cups of water in 6 second s. What is the constant proportionality for the relationship of cups of water to minutes
Answers
Related Questions
A runner is running a 10 km race. It takes her 17.5 minutes to reach the 2.5 km mark. at that rate, how long would it take her to run the whole race?
Answers
Answer:
time = 70 minutes
verify that the indicated family of functions is a solution of the given differential equation. Assume an appropriate interval of the definition for each solution
dP/dt= P(1-P); P= C1e^t /(1+C1e^t )
Answers
The family of functions P = C1e^t / (1 + C1e^t) is a solution to the differential equation dP/dt = P(1 - P) on an appropriate interval of definition.
In the first paragraph, we summarize that the family of functions P = C1e^t / (1 + C1e^t) is a solution to the differential equation dP/dt = P(1 - P). This equation represents the rate of change of the variable P with respect to time t, and the solution provides a relationship between P and t. In the second paragraph, we explain why this family of functions satisfies the given differential equation.
To verify the solution, we can substitute P = C1e^t / (1 + C1e^t) into the differential equation dP/dt = P(1 - P) and see if both sides are equal. Taking the derivative of P with respect to t, we have:
dP/dt = [d/dt (C1e^t / (1 + C1e^t))] = C1e^t(1 + C1e^t) - C1e^t(1 - C1e^t) / (1 + C1e^t)^2
= C1e^t + C1e^(2t) - C1e^t + C1e^(2t) / (1 + C1e^t)^2
= 2C1e^(2t) / (1 + C1e^t)^2.
On the other hand, evaluating P(1 - P), we get:
P(1 - P) = (C1e^t / (1 + C1e^t)) * (1 - C1e^t / (1 + C1e^t))
= (C1e^t / (1 + C1e^t)) * (1 - C1e^t + C1e^t / (1 + C1e^t))
= (C1e^t - C1e^(2t) + C1e^t) / (1 + C1e^t)
= (2C1e^t - C1e^(2t)) / (1 + C1e^t)
= 2C1e^t / (1 + C1e^t) - C1e^(2t) / (1 + C1e^t).
Comparing the two sides, we see that dP/dt = P(1 - P), which means the family of functions P = C1e^t / (1 + C1e^t) is indeed a solution to the given differential equation.
Learn more about differential equation here:
https://brainly.com/question/25731911
#SPJ11
Please look at the picture.

Answers
Answer:
Blue
Step-by-step explanation:
I graphed it, and got the same thing.
What is the nth term rule of the linear sequence below?
27, 25, 23, 21, 19, ...
Answers
Answer:
Step-by-step explanation:
Comment
This is an arithmetic series. It has the following givens.
a = 27 The first term
d = - 2 The difference between one term and the one behind it.
n = quite small
Tn = a + (n - 1)*d
tn = 27 - 2n + 2
tn = 29 - 2n
Workers have packed 1,400 glasses in 7 boxes. If they pack 3 more boxes, how many glasses will they have packed in all?
Answers
1box = 1400/7 = 200
200×3=600
1400+600=2000
Step-by-step explanation:
Given :Workers have packed 1,400 glasses in 7 boxes.
To Find :If they pack 3 more boxes, how many glasses will they have packed in all?
Solution:
Workers packed no. of glasses in 7 boxes = 1400
Workers packed no. of glasses in 1 box =
Workers packed no. of glasses in 3 boxes =
=
So, initially they packed 1400 glasses
If they pack 3 more boxes so, the pack 600 glasses more
So, The total no. of glasses have packed by workers = 1400+600 = 2000
Hence they have packed 2000 glasses in all.
What is the remainder when f(x) = 3x3 + 24x2 − 45x − 162 is divided by (x + 8)?
Answers
The remainder when f(x) = 3x³ + 24x² − 45x − 162 is divided by (x + 8) is 198.
How to find the remainder when dividing polynomial?A polynomial is defined as an expression which is composed of variables, constants and exponents, that are combined using mathematical operations such as addition, subtraction, multiplication and division.
Therefore, the remainder when f(x) = 3x³ + 24x² - 45x - 162 is divided by (x + 8) is as follows:
The dividend is x + 8.
Hence, let's Set the dividend to 0
x + 8 = 0
x = -8
Substitute x = - 8 in f(x) = 3x³ + 24x² - 45x - 162
f(-8) = 3(-8)³ + 24(-8)² - 45(-8) - 162
f(-8) = - 1536 + 1536 + 360 - 162
f(-8) = 198
Therefore, the remainder is 198.
learn more on polynomial here: https://brainly.com/question/28224762
#SPJ1
on the planet Jupiter, a ball this thrown upward at a velocity at 10m/s. It's height, h(t) meters after t seconds is given by the equation h(t)=-12.5(t-0.4)^2+4.
a) what is the maximum height the ball reaches?
b) what was the height of the ball when it was released from the throwers hand?
c) how many seconds after the ball was hit and did it land on the surface of Jupiter to the nearest second?
Answers
Answer:
a) The maximum height that the ball reaches is 4 meters.
b) The height of the ball when it is released from thrower's hand is 2 meters.
c) The ball will take approximately 0.966 seconds to hit the surface of Jupiter.
Step-by-step explanation:
a) Let \(h(t) = -12.5\cdot (t-0.4)^{2}+4\), where \(t\) and \(h(t)\) are the time and height, measured in seconds and meters. Since this equation is in vertex form, the maximum height corresponds to the value associated with the dependent variable (height). That is:
\(h(t) -4 = -12.5\cdot (t-0.4)^{2}\)
Hence, the maximum height that the ball reaches is 4 meters.
b) The height of the ball when the ball is released from thrower's hand is the height of the ball at \(t = 0\,s\). Then, we evaluate the function:
\(h(0) = -12.5\cdot (0-0.4)^{2}+4\)
\(h(0) = 2\,m\)
The height of the ball when it is released from thrower's hand is 2 meters.
c) The instants when the ball hits the ground are those instants \(t\) so that \(h(t) = 0\). Then:
\(-12.5\cdot (t-0.4)^{2}+4 = 0\)
\(-12.5\cdot (t^{2}-0.8\cdot t +0.16)+4 = 0\)
\(-12.5\cdot t^{2}+10\cdot t +2 = 0\)
By the Quadratic Formula we obtain the following roots:
\(t_{1} \approx 0.966\,s\), \(t_{2}\approx -0.166\,s\)
Only the first root is physically reasonable, since time is a positive real variable.
The ball will take approximately 0.966 seconds to hit the surface of Jupiter.
Kelly is knitting a scarf for her brother. It took her 1/5 hour to knit 2/5 foot of the scarf. How fast is Kelly’s knitting speed, in feet per hour?
You help me I help you!
Answers
Answer: 9/8 feet per hour fast is Kelly's knitting speed
Step-by-step explanation:
Unit rate defined as the rates are expressed as a quantity 1 such as 4 meters per second or 4 miles per hour.
As per the statement:
Kelly is knitting a scarf for her brother. it took her 1/3 hour to knit 3/8 foot of the scarf.
She took /3 hours to knit 3/8 foot of the scarf.
Therefore, 9/8 feet per hour fast is Kelly's knitting speed.
Hope I helped!
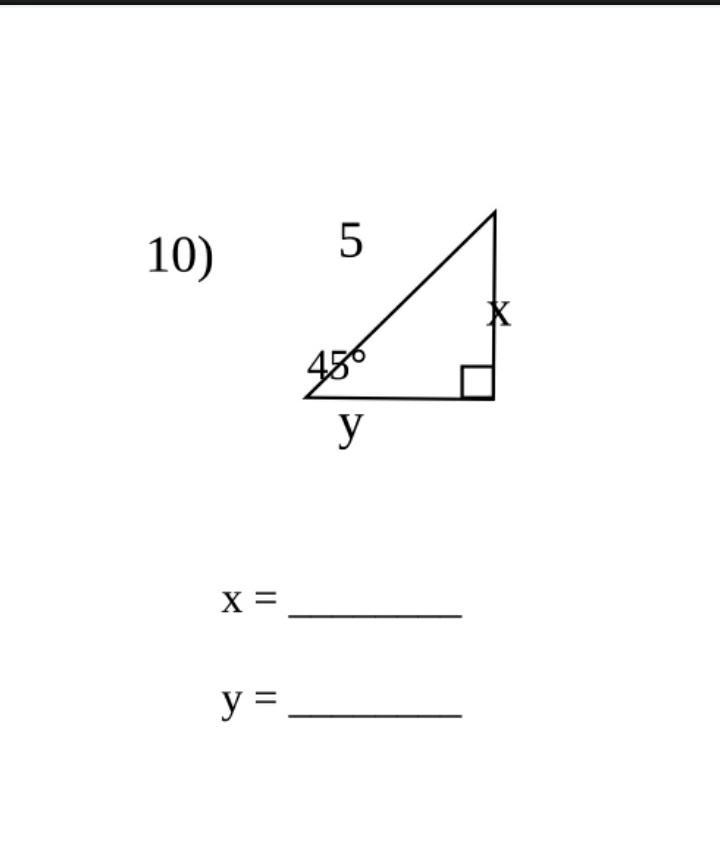
How do I find the missing sides for this special right triangle?

Answers
Find the linearization L(x) of f(x) at x a: f(x)=x+1/x, a=1 f(x) = squareroot x^2+9, a = -4
Answers
The linearization of f(x) at x=1 is L(x) = 1 and the linearization of f(x) at x=-4 is L(x) = 1 - (4/5)x
Linearization is the process of approximating a function using a linear equation, which can be useful in making calculations easier or understanding the behavior of a function near a specific point. To find the linearization L(x) of f(x) at x=a, we can use the formula:
L(x) = f(a) + f'(a)(x-a)
where f'(a) is the derivative of f(x) evaluated at x=a.
For the first function, f(x) = x+1/x and a=1, we can find f'(x) using the quotient rule:
\(f'(x) = (1 - 1/x^{2})\)
Evaluating this at x=1 gives us:
\(f'(1) = (1 - 1/1^{2}) = 0\)
Plugging in the values we have found into the formula for linearization, we get:
L(x) = f(1) + f'(1)(x-1)
L(x) = 1 + 0(x-1)
L(x) = 1
Therefore, the linearization of f(x) at x=1 is L(x) = 1.
For the second function, \(f(x) = \sqrt{(x^{2}+9)}\) and a=-4, we can find f'(x) using the chain rule:
\(f'(x) = (1/2)(x^{2}+9)^{-1/2}(2x)\)
Evaluating this at x=-4 gives us:
\(f'(-4) = (1/2)((-4)^{2}+9)^{-1/2}(-8)\)
f'(-4) = -4/5
Plugging in the values we have found into the formula for linearization, we get:
L(x) = f(-4) + f'(-4)(x+4)
\(L(x) = \sqrt{(-4)^{2}+9} - (4/5)(x+4)\)
\(L(x) = \sqrt{25} - (4/5)(x+4)\)
L(x) = 5 - (4/5)(x+4)
L(x) = 1 - (4/5)x
Therefore, the linearization of f(x) at x=-4 is L(x) = 1 - (4/5)x.
Learn more about linearization here:
https://brainly.com/question/31332050
#SPJ11
please help and show work

Answers
Answer:
Step-by-step explanation:
\(7^{2} +x^{2} =24^{2} \\49+x^{2} =576\\x^{2} =418\\x=\sqrt{418}\)
What is the range of the function f(x) = |x| – 3?
{f(x) ∈ ℝ | f(x) ≥ –3}
{f(x) ∈ ℝ | f(x) < –3}
{f(x) ∈ ℝ | f(x) ≤ –3}
{f(x) ∈ ℝ | f(x) > –3}
Answers
Answer:
{f(x) ∈ ℝ | f(x) ≥ –3}
Step-by-step explanation:
f(x)=|x|-3
|x| have range x≥0 .
f(x)≥0-3
f(x)≥-3
First answer {f(x) ∈ ℝ | f(x) ≥ –3}
The discrete time open loop transfer function of a certain control system is G(z)= (0.98z+0.66)/[(z-1)(z-0.368)]. The steady state error for unity ramp input is: Select one: O a. T/2.59 b. T/3.59 C. 3.59T d. 4.59T e. T/4.59
Answers
The steady-state error for a unity ramp input is approximately T/1.739. None of the provided answer options match this result.
To find the steady-state error for a unity ramp input, we can use the final value theorem. The steady-state error for a unity ramp input is given by the formula:
ESS = lim[z→1] (1 - G(z) * z^(-1))/z
Given the open-loop transfer function G(z) = (0.98z + 0.66)/[(z - 1)(z - 0.368)], we can substitute this into the formula:
ESS = lim[z→1] (1 - [(0.98z + 0.66)/[(z - 1)(z - 0.368)]] * z^(-1))/z
Simplifying this expression:
ESS = lim[z→1] [(z - 0.98z - 0.66)/[(z - 1)(z - 0.368)]]/z
Now, let's substitute z = 1 into the expression:
ESS = [(1 - 0.98 - 0.66)/[(1 - 1)(1 - 0.368)]]/1
ESS = [(-0.64)/(-0.368)]/1
ESS = 1.739
To learn more about steady-state:
brainly.com/question/30760169
#SPJ11
Determine if XY is tangent to circle Z.
8
10
Z
O Yes
Ο No

Answers
The correct option is NO, the line XY is not tangent to the circle Z.
Tangent to a circle theoremThe tangent to a circle theorem states that a line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency
For the line XY to be tangent to the circle Z implies line XZ is perpendicular to line XY which will make the triangle XYZ a right triangle
So by Pythagoras rule, the sum of the square for the sides XZ and XY must be equal to the square of YZ, otherwise, XY is not a tangent to the circle Z
XY² = 5² = 25
XZ² + XY² = 8² + 10² = 164.
In conclusion, since XZ² + XY² is not equal to XY², then XY is not tangent to the circle Z.
Read more about tangent to a circle here:https://brainly.com/question/11067500
#SPJ1
PLSS HELP ME ASAP!! I WILL GIVE YOU BRAINLYEST!
A tree casts a 9-foot shadow while a 5-foot
pole casts a 2h foot shadow. How tall is the
tree?

Answers
the answer tho this is that the tree is 14ft
Answer:
22.5
Step-by-step explanation:
20 ft for an 8 foot shadow but since you need 1 more foot
take half of 5 (2.5) and you get 22.5
1 and 2 are vertical angles. If the
measure of 22 is 105°, find the measure of
Answers
wave interference that results in greater wave amplitude is called_____.
Answers
Wave interference that results in greater wave amplitude is called Constructive interference.
What is Wave Interference?
Wave interference is a physical phenomena that occurs when two waves collide while traveling through the same medium. Waves interact in two ways.
a) Constructive Interference - In this case, the two waves cancel each other out because their amplitudes are equal and opposite.
b) Destructive Interference - This occurs when two waves add to each other as they travel in the same direction, resulting in a wave with a longer wavelength.
It is Constructive interference.
Therefore, Wave interference that results in greater wave amplitude is called Constructive interference.
To know more about Wave Interference visit,
https://brainly.com/question/12466679
#SPJ4
SOMEONE HELP!!! AHHHH!!!

Answers
Hey there! :)
Answer:
The first option:
Y-intercept: 9
Zeros: 1, -1, 3, -3
Step-by-step explanation:
The Y-intercept is where the graph intersects with the y-axis. On this graph, we can see that the graph intersects at y = 9.
The zeros of the graph are where the graph intersects the x-axis. When looking at the graph, the x-axis is intersected at x = -3, x = -1, x = 1, and x = 3.
Therefore, A, or the first option, is the correct answer.
Answer:
y : 9
Step-by-step explanation:
The illumination of a light source varies inversely with the square of
the distance from that source. At a distance of 120 meters away from
the source, the illumination is 20 lux. What is the formula for the
illumination, E, in lux, as a function of the distance, d, from the source,
in meters?
Answers
E = 2400/d is the equation for the illumination, E, in lux as a function of the source's distance, d, in meters.
Solving variation problemsFrom the given problem, we can let the illumination of light be 'E' and the distance from the source be 'd' such that if the illumination of a light source varies inversely with the square of the distance from that source, we will have:
E α 1/d
E = k/d
Given the following
d = 120 m
E = 20 lux
Substitute
20 = k/120
k = 2400
Determine the equivalent formula
E = 2400/d
Therefore the formula for the illumination, E, in lux, as a function of the distance, d, from the source in meters is E = 2400/d
Learn more on inverse proportion here: https://brainly.com/question/30095787
#SPJ1
What is multiplicative inverse of 15/-4?
Answers
Answer:
-3.75
Step-by-step explanation:
Which numbers are arranged in order least to greatest

Answers
Answer:
D
Step-by-step explanation:
0.0516 = 0.0516
5/16 = 0.3125
16% = 0.16
0.05 = 0.05
From least to greatest:
0.05, 0.0516, 0.16, 0.3125
0.05, 0.0516, 16%, 5/16
Answer: D
Find the value of x and y
Answers
Answer:
5/\(\sqrt{2}\)
Step-by-step explanation:
This is an isosceles triangle, which means the hypotenuse is the product of one of the legs and the squareroot of 2. Since the hypotenuse is 5, the legs must be 5/\(\sqrt{2}\).
A rectangle has a length that is 8 less than it’s width w the perimeter is 52 which equation can be used to determine length
Answers
Answer:
width?
8-W-52
2(w-8) +2w=52
(W-8)+W=52
2(8-W) +2w=52
-1 1/5 + -3/5 in simplest form
Answers
Answer:
-1 4/5
Step-by-step explanation:
In mathematics, a fraction is a number that represents a part of a whole. It consists of a numerator and a denominator. The numerator represents the number of equal parts of a whole, while the denominator is the total number of parts that make up said whole. For example, in the fraction 3 5, the numerator is 3, and the denominator is 5. A more illustrative example could involve a pie with 8 slices. 1 of those 8 slices would constitute the numerator of a fraction, while the total of 8 slices that comprises the whole pie would be the denominator. If a person were to eat 3 slices, the remaining fraction of the pie would therefore be 5 8 as shown in the image to the right. Note that the denominator of a fraction cannot be 0, as it would make the fraction undefined. Fractions can undergo many different operations, some of which are mentioned below.
The total time, measured in units of 100 hours, that a teenager runs her hair dryer over a period of one year is a continuous random variable X that has the density function below. Use the theorem below to evaluate the mean of the random variable Y = 51X2 + 40X, where Y is equal to the number of kilowatt hours expended annually Theorem: The expected value of the sum or difference of two or more functions of a random variable X is the sum or difference of the expected values of the functions, as given by the formula below 0, elsewhere
Answers
Answer:
The mean of the random variable Y is (17/2) kilowatt hours.
Step-by-step explanation:
To find the expected value of Y, we can use the formula provided in the theorem:
E(Y) = E(51X^2 + 40X)
Using linearity of expectation, we can break this down into two separate expected values:
E(Y) = 51E(X^2) + 40E(X)
The given probability density function is, f(x) = (1/4)x, 0 ≤ x ≤ 2.
The expected value of a continuous random variable is calculated using the formula shown below, where E(x) is the expected value of x, and f(x) is the probability density function of x.
E(x) = ∫xf(x)dx
The expected value of the random variable X can be calculated as follows:
E(X) = ∫0² (1/4)x dx = (1/8) [x²]₀² = 1
E(X²) = ∫0² (1/4)x² dx = (1/12) [x³]₀² = (1/6)
Now we can substitute these values into our original equation:
E(Y) = E(51X² + 40X) = 51E(X²) + 40E(X) = 51(1/6) + 40(1) = (17/2) kilowatt hours.
Therefore, the mean of the random variable Y is (17/2) kilowatt hours.
Know more about mean of the random variable ,
https://brainly.com/question/29754021
#SPJ11
A callable bond pays annual interest of $60, has a par value of $1,000, matures in 20 years but is callable in 10 years at a price of $1,100, and has a value today of $1055.84. The yield to call on this bond is:
A. 6.00%
B. 6.58%
C. 7.20%
D. 8.00%
Answers
The PV function on a financial calculator to find the present value of the bond at different yield rates until we get a present value closest to $1,055.84. This method also gives a yield rate of approximately 6.58%.
To solve for the yield to call on the callable bond, we need to use trial and error or a financial calculator.
Using trial and error:
Assuming a yield-to-call rate of 6%, the present value of the bond would be:
PV = $60(PVIFA6%,10) + $1,000(PVIF6%,10) = $1,007.98
This is less than the given value of $1,055.84, so we need to try a higher yield rate. Continuing this process, we find that a yield rate of approximately 6.58% gives a present value closest to $1,055.84. Therefore, the answer is B. 6.58%.
Using a financial calculator:
We can use the PV function on a financial calculator to find the present value of the bond at different yield rates until we get a present value closest to $1,055.84. This method also gives a yield rate of approximately 6.58%.
To learn more about PV function visit:https://brainly.com/question/27008512
#SPJ11
Point D is located on the segment CE. IF CD = 24 and DE = x and CE - 5x, what is the measure of segment CE?
Answers
Answer:
30Step-by-step explanation:
If point D is located on the segment CE, then point C, D and E lies on the same line i.e they are collinear. Mathematically, CD+DE = CE
Given CD = 24 and DE = x and CE = 5x, on substituting this values in the equation we have;
\(24+x = 5x\\5x-x = 24\\4x = 24\\x = 24/4\\x = 6\)
Since CE = 5x, CE = 5(6) = 30
The measure of segment CE is 30
A farmer uses 1/3 of his land to grow corn and 1/4 to grow yams . What fraction of the land is left?
Answers
Answer:
7/12
Step-by-step explanation:
3*4=12. 4/12+3/12=7/12.
Answer:
5/12
Step-by-step explanation:
you find the common factor of 12, divide 12 by the denominator, multiply the numerator by that, add the new numerators, put it on the denominator of 12, subtract it from 12/12
The vertices of a triangle are P(7. -4), Q(-7, -8), and R(8,4). Name the vertices of the image
reflected in the y-axis.
Answers
Answer:
P' (-7, -4) , Q' (7, -8) , R' (-8, 4)
Step-by-step explanation:
Reflection in the y -axis:
The rule for a reflection over the y-axis is (x, y) → (−x, y).
P (7, -4) → P' (-7, -4)
Q (-7, -8) → Q' (7, -8)
R (8, 4) → R' (-8, 4)
38 / 10000 word limit38 words written of 10000 allowed question 2 (b) suppose the specialist wants to know the number of suspicious transactions that will need to be reviewed until reaching the first transaction that will be blocked. (i) define the random variable of interest and state how the variable is distributed.
Answers
The expected value of blocked transactions by the specialist is 54.4. The random variable of interest is the number of reviews until the first block is found which follows a geometric distribution.
a) The expected value refers to a generalization of the weighted average. In an experiment with number of n trails and probability of success on a single trail p, the expected value of blocked transaction is given by:
E(X) = np where n is the number of trails and p is the probability of transaction block is 0.4.
Hence,
E(X) = 136*0.4 = 54.4
b) The random variable of interest be the random variable X represents the number of reviews until the first block is found. X follows a geometric distribution as it is used to model the first transaction.
Note: The question is incomplete. The complete question probably is: At a financial institution, a fraud detection system identifies suspicious transactions and sends them to a specialist for review. The specialist reviews the transaction, the customer profile, and past history. If there is sufficient evidence of fraud, the transaction is blocked. Based on past history, the specialist blocks 40 percent of the suspicious transactions. Assume a suspicious transaction is independent of other suspicious transactions. (a) Suppose the specialist will review 136 suspicious transactions in one day. What is the expected number of blocked transactions by the specialist? Show your work. (b) Suppose the specialist wants to know the number of suspicious transactions that will need to be reviewed until reaching the first transaction that will be blocked. Define the random variable of interest and state how the variable is distributed.
Learn more about Expected value:
https://brainly.com/question/24305645
#SPJ4