Verify that the function satisfies the three hypotheses of Rolle's Theorem on the given interval. Then find all numbers c that satisfy the conclusion of Rolle's Thesrem. (Enter your answers separated list.) f(x)-5-6x + 3x², [0, 21 C- Need Help? Mead comme
Verify that the function satisfies the three hypotheses of Rolle's Theorem on the given interval. Then find all numbers that satisfy the conclusion of Rolle's Theorem. (Enter your answers as a comme separated list.) MX) -√x-x 10.91 Need Help? www.
If f(4) = 15 and f '(x) ≥ 2 for 4 ≤ x ≤ 6, how small can f(6) possibly be? Need Help? Read It Watch It
Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? x)=x²+2x+4, [-1, 1) O Yes, it does not matter if fis continuous or differentiable; every function satisfies the Mean Value Theorem. O There is not enough information to verify if this function satisfies the Mean Value Theorem. No, Fis not continuous on [-1, 1]. OYes, is continuous on [-1, 1] and differentiable on (-1, 1) since polynomials are continuous and differentiable on No, ris continuous on (-1, 1] but not differentiable on (-1, 1). If it satisfies the hypotheses, find all numbers c that satisfy the conclusion of the Mean Value Theorem.
Answers
For the function f(x) = 5 - 6x + 3x² on the interval [0, 21], Rolle's Theorem can be applied. The function satisfies all three hypotheses of Rolle's Theorem: it is continuous on the closed interval [0, 21], it is differentiable on the open interval (0, 21), and the function values at the endpoints are equal. Therefore, there exists at least one number c in the open interval (0, 21) such that f'(c) = 0.
To apply Rolle's Theorem, we need to check the three hypotheses:
1. The function f(x) = 5 - 6x + 3x² is continuous on the closed interval [0, 21] because it is a polynomial, and polynomials are continuous for all real numbers.
2. The function f(x) = 5 - 6x + 3x² is differentiable on the open interval (0, 21) because it is a polynomial, and polynomials are differentiable for all real numbers.
3. The function values at the endpoints of the interval are equal: f(0) = 5 and f(21) = 5 - 6(21) + 3(21)² = 5 - 126 + 1323 = 1202.
Since all three hypotheses are satisfied, Rolle's Theorem guarantees the existence of at least one number c in the open interval (0, 21) such that f'(c) = 0. To find this number, we need to find the derivative of f(x):
f'(x) = -6 + 6x.
Setting f'(x) = 0, we have:
-6 + 6x = 0.
Solving this equation, we find x = 1.
Therefore, the conclusion of Rolle's Theorem is satisfied at x = 1.
Learn more about function here : brainly.com/question/30721594
#SPJ11
Related Questions
-108y^4 - 4y
I just need the steps, screw the answer if you want.
Answers
Answer:
-4y(3y + 1) (9y^2 - 3y + 1)
Step-by-step explanation:
-108y^4 - 4y
= -4y(27y^3 + 1)
= -4y(3y + 1) (3^2y^2 - 3y + 1)
= -4y(3y + 1) (9y^2 - 3y + 1)
Answer:
-4y(3y + 1) (9y^2 - 3y + 1)
e:
The dimensions of the base of Box 2 are:
a.width: x; length: 3
b.width: x; length: 4x - 1
c.width: x, length: x - 4
d.width: x, length: 4x + 1
DONE
Answers
Answer:
b
Step-by-step explanation:
Answer:
B
Step-by-step explanation:
Got it right on Edge 2020
Im doing an extra practice and need help with this one problem

Answers
Answer:
it might be this 8.74777778 im not sure if it is tho so if im wrong then im sorry
Step-by-step explanation:
when testing the difference between two independent samples, which test occurs when the null hypothesis states the difference between the parameters is less than or equal to zero, and the alternative hypothesis states that the difference is greater than zero?
Answers
The alternative hypothesis states that the difference is greater than zero.
What Are Tails in a Hypothesis Test?
First, we need to cover some background material to understand the tails in a test. Typically, hypothesis tests take all of the sample data and convert it to a single value, which is known as a test statistic. You’re probably already familiar with some test statistics.
For example, t-tests calculate t-values. F-tests, such as ANOVA, generate F-values. The chi-square test of independence and some distribution tests produce chi-square values. All of these values are test statistics.
Keep in mind that this t-distribution assumes that the null hypothesis is correct for the population. Consequently, the peak (most likely value) of the distribution occurs at t=0, which represents the null hypothesis in a t-test. Typically, the null hypothesis states that there is no effect. As t-values move further away from zero, it represents larger effect sizes. When the null hypothesis is true for the population, obtaining samples that exhibit a large apparent effect becomes less likely, which is why the probabilities taper off for t-values further from zero.
Hence the answer is the alternative hypothesis states that the difference is greater than zero.
To learn more about null hypothesis click here https://brainly.com/question/4436370
#SPJ4
Find the average value of F(x, y, z) = z over the region bounded below by the xy-plane, on the sides by the sphere
x2 + y2 + z2 = 36, and bounded above by the cone ϕ = (pi/3).
Answers
The average value of F(x, y, z) = z over the region bounded below by the xy-plane, on the sides by the sphere \(x^2 + y^2 + z^2 = 36\), and bounded above by the cone ϕ = (pi/3) is -ρ\(^4 / 2304.\)
To find the average value of the function F(x, y, z) = z over the given region, we need to compute the triple integral of F(x, y, z) over the region and divide it by the volume of the region.
The region is bounded below by the xy-plane, on the sides by the sphere \(x^2 + y^2 + z^2 = 36\), and bounded above by the cone φ = (π/3).
In spherical coordinates, the sphere can be represented as ρ = 6, and the cone can be represented as φ = (π/3).
To set up the integral, we need to determine the limits of integration for each variable. Since the region is symmetric with respect to the xy-plane, we can integrate over one-half of the region and multiply the result by 2.
Let's integrate over the region in spherical coordinates:
0 ≤ ρ ≤ 6
0 ≤ φ ≤ (π/3)
0 ≤ θ ≤ 2π
The integral to compute the average value is:
2 * ∫∫∫ F(ρsin(φ)cos(θ), ρsin(φ)sin(θ), ρcos(φ)) ρ\(^2 sin\)(φ) dρ dφ dθ
Now, we substitute F(x, y, z) = z into the integral:
2 * ∫∫∫ ρcos(φ) ρ\(^2sin\)(φ) dρ dφ dθ
Evaluate the innermost integral first:
∫[0 to 6] ρ\(^3cos\)(φ)sin(φ) dρ = (1/4)ρ\(^4cos\)(φ)sin(φ)
Now, integrate with respect to φ:
∫[0 to π/3] (1/4)ρ\(^4cos\)(φ)sin(φ) dφ = (1/4)ρ\(^4[-(cos\)(φ))\(^2]\) [0 to π/3]
= (1/4)ρ\(^4(-1/4)\)
= -ρ\(^4/16\)
Now, integrate with respect to θ:
∫[0 to 2π] -ρ\(^4/16\) dθ = -ρ\(^4/16\) * 2π
= -πρ\(^4/8\)
Finally, we divide this result by the volume of the region to find the average value:
Volume of the region = (1/2) * Volume of the sphere
= (1/2) * (4/3) * π * (\(6^3\))
= 288π
Average value = (-πρ\(^4/8\)) / (288π)
= -ρ\(^4 / (2304)\)
Therefore, the average value of F(x, y, z) = z over the given region is -ρ\(^4 / 2304.\)
Learn more about Limits of Integration at
brainly.com/question/32233159
#SPJ4
How is the tax base of an area calculated?.
Answers
The total market value of all the assets, properties, and income in a given region or jurisdiction is what is referred to as the tax base. The tax base must be multiplied by the tax rate to determine the overall tax obligation: Tax Base x Tax Rate equals Tax Liability.
Describe the tax base?
The whole amount of income, property, assets, consumption, transactions, or other economic activity that a tax authority is allowed to tax is known as the tax base.
What is tax base formula?
Multiplying the tax base by the tax rate yields the tax obligation. The tax liability divided by the tax rate would be the result. Tax Liability/Tax Rate in the Tax Base Formula.Learn more about tax base
brainly.com/question/20127586
#SPJ4
answer for brainilest and 11 points

Answers
Answer:
Top right corner
Step-by-step explanation:
3PLEASE HELP ME THIS IS URGENT I WILL GIVE BRAINLIEST
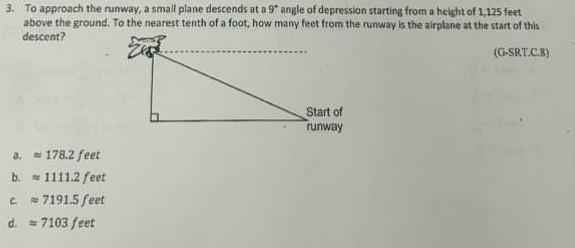
Answers
Answer: x= 7191.509 ft
Step-by-step explanation:
Sin9/1 = 1125/x
X/1 = 1125/sin9
how many ways are there to win the jackpot? how many ways are there to match 5 of 6 numbers? how many ways are there to match 4 of 6 numbers? how many ways are there to match 3 of 6 numbers?
Answers
The number of ways to match 5 of 6 numbers is 6 ways
The number of ways to match 4 of 6 numbers is 15 ways
The number of ways to match 3 of 6 numbers is 20 ways
To calculate number of ways to match 5 of 6 numbers we have to use to formula:
\(nCr =\frac{n!}{(n - r)! . r !}\)
\(6C5=\frac{6!}{(6-5)! . 5!}\)
\(6C5=\frac{6!}{(1)! . 5!}\)
\(6C5=\frac{6.5.4.3.2.1}{1.5.4.3.2.1}\)
\(6C5=\frac{6}{1}\)
\(6C5= 6 \ ways\)
∴ 6 ways are to match 5 of 6 numbers
To calculate number of ways to match 4 of 6 numbers we have to use to formula:
\(nCr =\frac{n!}{(n - r)! . r !}\)
\(6C4=\frac{6!}{(6-4)! . 4!}\)
\(6C4=\frac{6!}{(2)! . 4!}\)
\(6C4=\frac{6.5.4.3.2.1}{2.1.4.3.2.1}\)
\(6C4=\frac{30}{2}\)
\(6C4= 15 \ ways\)
∴ 15 ways are to match 4 of 6 numbers
To calculate number of ways to match 4 of 6 numbers we have to use to formula:
\(nCr =\frac{n!}{(n - r)! . r !}\)
\(6C3=\frac{6!}{(6-3)! . 3!}\)
\(6C3=\frac{6!}{(3)! . 3!}\)
\(6C3=\frac{6.5.4.3.2.1}{3.2.1.3.2.1}\)
\(6C3=\frac{120}{6}\)
\(6C3= 20 \ ways\)
∴ 20 ways are to match 3 of 6 numbers
Learn more about Jackpots here :
https://brainly.com/question/27116420
#SPJ4
Consider selecting two elements, a and b, from the set A = {a, b, c, d, e}. List all possible subsets of A using both elements. (Remember to use roster notation. ie. {a, b, c, d, e}) List all possible arrangements of these two elements.
Answers
Possible subsets of A using two elements are:
{a, b}, {a, c}, {a, d}, {a, e},
{b, c}, {b, d}, {b, e},
{c, d}, {c, e},
{d, e}
Possible arrangements of these two elements are:
ab, ac, ad, ae,
bc, bd, be,
cd, ce,
de
To learn more about subsets refer below
https://brainly.com/question/30968366
#SPJ11
State whether the given measurements determine zero, one, or two triangles.
A = 61°, a = 23, b = 24
Answers
Answer:
One
Step-by-step explanation:
Find the value of B
Applying the law of sines
\(\frac{a}{sin(A)}\) = \(\frac{b}{sin(B)}\)
substitute the given values
\(\frac{23}{sin(61)}\) = \(\frac{24}{sin(B)}\)
sin (B) = \(\frac{24}{23}\)Sin(61)
step 2
Find the measure of angle C
Remember that the sum of the interior angles in any triangle must be equal to 180 degrees
so
61 + 65.87 + C = 180
C = 53.13
step 3
Find the value of c
Applying the law of sines
\(\frac{a}{sin(A)}\) = \(\frac{c}{sin(C)}\)
substitute the given values
\(\frac{23}{sin(61)}\) = \(\frac{c}{sin(53.13)}\)
c = \(\frac{23}{sin(61)}\)SIN (53.13)
C=21.04 units
so
there can only be one value for each measurement, therefore there can only be one triangle
Answer:
The answer is 2 triangles
Step-by-step explanation:
I took the test.
A distribution has a mean of 16 and a standard deviation of 6. What is the z score that corresponds with 25?.
Answers
Using the normal distribution formula, we know that the z score that is equivalent to 25 is 1.5.
What is a normal distribution?A continuous probability distribution for a real-valued random variable in statistics is known as a normal distribution or Gaussian distribution.
The characteristics of normal distributions are as follows: Bell-like in its symmetry.
The distribution's mean and median, which are both at its center, are equal.
68 percent of the data, or approximately, falls within one standard deviation of the mean.
So, the formula is used to determine the Z score for a data point x in a normal distribution:
Z = z - mean/standard deviation
Now, use the formula to calculate the z value as follows:
Z = z - mean/standard deviation
Z = 25 - 16/6
Z = 9/6
Z = 3/2
Z = 1.5
Therefore, using the normal distribution formula, we know that the z score that is equivalent to 25 is 1.5.
Know more about a normal distribution here:
https://brainly.com/question/4079902
#SPJ4
The figure shows two right triangles, each with its longest side on the same line. R 4 How long is XY? Type the answer in the box.

Answers
Answer: 6
Step-by-step explanation:
Because corresponding sides of similar triangles are proportional,
\(\frac{XY}{3}=\frac{4}{2}\\ \\ \frac{XY}{3}=2\\ \\ XY=\boxed{6}\)
the fraction of girls at the dance is
PLEASE DO THIS QUICK

Answers

Find the general solution of the given differential equation.
(x + 1) dy/dx + (x + 2)y = 2xe^-x
y=
Answers
The solution involves an integral that cannot be evaluated in closed form, so the answer cannot be simplified further.
How to solve the given differential equation (DE)?To solve the given differential equation (DE), we can use the integrating factor method. The steps are as follows:
1. Multiply both sides of the DE by the integrating factor, which is the exponential of the integral of the coefficient of y. In this case, the coefficient of y is (x + 2), so the integrating factor is e^(∫(x+2)dx) = e^(x^2/2 + 2x).
So, we have: (x + 1) e^(x^2/2 + 2x) dy/dx + (x + 2) e^(x^2/2 + 2x) y = 2x e^(x^2/2 + 2x) e^(-xy)
2. Notice that the left-hand side of the DE is the product of the derivative of y with respect to x and the integrating factor, so we can apply the product rule of differentiation to obtain:
d/dx [ e^(x^2/2 + 2x) y ] = 2x e^(x^2/2 + 2x) e^(-xy)
3. Integrate both sides of the previous equation with respect to x to obtain:
e^(x^2/2 + 2x) y = - e^(-xy) + C
where C is the constant of integration.
4. Solve for y by dividing both sides by the integrating factor:
y = [- e^(-xy) + C] e^(-x^2/2 - 2x)
This is the general solution of the given DE.
Note that the solution involves an integral that cannot be evaluated in closed form, so the answer cannot be simplified further.
Learn more about equation
brainly.com/question/29538993
#SPJ11
Answer please VVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVVV

Answers
\(\left[\begin{array}{ccc}3 & 9 \\\\ 5& -2\end{array}\right]+\left[\begin{array}{ccc}6 & 0\\\\ \!\!-8 & 4\end{array}\right]=\left[\begin{array}{ccc} 3+6 & 9+0 \\\\5-8 &-2+4 \end{array}\right] =\left[\begin{array}{ccc} 9& 9 \\\\ -3 & 2\end{array}\right]\)
A marble statue has a mass of 1600 kg and is
270 cm tall.
The density of marble is 2500 kg/m³.
Justin makes a mathematically similar model
of the statue out of clay.
The model is 45 cm tall and has a density of
1200 kg/m³.
What is the mass of Justin's model?
Give your answer to 3 significant figures

Answers
Answer:
3.56 kg
Step-by-step explanation:
You want the mass of a model that is 45 cm tall and has a density of 1200 kg/m³ when the statue it is modeling is 270 cm tall, has a density of 2500 kg/m³, and a mass of 1600 kg.
VolumeThe ratio of volumes of the model to the statue is the cube of the ratio of their heights:
Vm/Vs = (Hm/Hs)³
Vm = Vs(Hm/Hs)³ = (1600 kg)/(2500 kg/m³)·((45 cm)/(270 cm))³
Vm ≈ 0.002963 m³
MassThe mass of the model is the product of its volume and its density:
Mm = Vm·ρ = (0.002963 m³)(1200 kg/m³) ≈ 3.56 kg
The mass of Justin's model is about 3.56 kg.
__
Additional comment
The relationship between density, volume, and mass is ...
ρ = mass/volume
This can be rearranged to ...
volume = mass/ρ
Which is the expression we used for Vs in the first section above.
(We used V and H for volume and height with 'm' and 's' signifying the model and the statue, respectively.)
<95141404393>

The mass of Justin's model is approximately 3.57 kg., rounded to 3 significant figures.
How to find the mass of Justin's modelTo find the mass of Justin's model, we can use the concept of mathematical similarity.
Mathematical similarity means that corresponding dimensions of two objects are proportional. In this case, Since the densities are also given, we can use the volume ratio to find the mass ratio.
Let's calculate the volume ratio first:
Volume ratio = (Height of model / Height of statue)^3
= (45 cm / 270 cm)^3
= (0.1667)^3
= 0.00463
Now, using the density ratio:
Density ratio = Density of model / Density of statue
= 1200 kg/m³ / 2500 kg/m³
= 0.48
Finally, we can find the mass of Justin's model by multiplying the mass of the statue by the volume ratio and density ratio:
Mass of Justin's model = Mass of statue * Volume ratio * Density ratio
= 1600 kg * 0.00463 * 0.48
= 3.5712 kg
Rounding to 3 significant figures, the mass of Justin's model is approximately 3.57 kg.
Learn more about mass at https://brainly.com/question/86444
#SPJ1
What is the LCM of 20, 10 and 50?
1.50
2.100
3.10
4.200
Answers
Step-by-step explanation:
2 _|_20, 10, 50
5 _|_ 10, 5, 25
1 _|_ 2, 1, 5
Further, it is not divisible.
So, LCM = 2×5×2×5
LCM = 100 is the answer.
Hope it helps :)
\(.\)
choose the table thst represents g(x) =-2•f(x) when f(x) = x +4

Answers
Answer:
c
Step-by-step explanation:
x=1 g(x)=-10
x=2 g(x)=-12
x=3 g(x)=-14
f(x)=x+4
=> g(x)=-2·(x+4)
Isabella has some dimes and some quarters. She has at most 25 coins worth a minimum of $4. 45 combined. If isabella has 17 dimes, determine all possible values for the number of quarters that she could have. Your answer should be a comma separated list of values. If there are no possible solutions, submit an empty answer.
Answers
Number of quarters is at least 13 and Number of dimes is at most 12 when Isabella has a few quarters and dimes. She has a total of 25 coins, totaling a minimum of $4.45.
Given that,
Isabella has a few quarters and dimes. She has a total of 25 coins, totaling a minimum of $4.45.
We have to find write an inequality system to get every feasible value for the number of quarters (q) and dimes (d) that Isabella could have if she has 17 dimes.
We know that,
Let the number of dimes be x and number of quarters by y.
10 dimes = $ 1
Therefore, 1 dime = $ 10
4 quarters = $ 1
Therefore, 1 quarter = $ 1/4
Isabella has at most 25 coins i.e.
Number of dimes +Number of quarters≥ 25
x+y≥25------>Equation(1)
Total worth of the coins is at least $ 4.45
Number of dime ×value of 1 dimes + Number of quarters × value of 1 quarters≥4.45
x/10+y/4≥4.45
2x+5y≥89------>Equation(2)
Multiply 2 to equation(1) subtract to equation(2)
2x+2y≥50
2x+5y≥89
----------------
0-3y≥-39
3y≥39
y≥39/3
y≥13
Substitute y in equation(1)
x+y≥25
x+13≥25
x≥12
Therefore, Number of quarters is at least 13 and Number of dimes is at most 12 when Isabella has a few quarters and dimes. She has a total of 25 coins, totaling a minimum of $4.45.
To learn more about quarters visit: https://brainly.com/question/391885
#SPJ4
Choose a company with your option and explain how
that company can create a business model? There are 8 steps in the
business module, explain each step based on the company which you
have chosen.
Answers
Company: Amazon, 8 Steps in the Business Model: Define the value proposition. What value does Amazon offer its customers? Amazon offers a convenient and affordable way to shop for a wide variety of products.
Identify the target market. Who are Amazon's customers? Amazon's target market is people who want to buy products online.
Determine the revenue streams. How does Amazon make money? Amazon makes money through product sales, advertising, and subscription fees.
Assess the cost structure. What are Amazon's costs? Amazon's costs include salaries, rent, and marketing.
Develop a marketing plan. How will Amazon reach its target market? Amazon's marketing plan includes online advertising, search engine optimization, and social media marketing.
Create a sales strategy. How will Amazon sell its products? Amazon's sales strategy includes a focus on customer service and convenience.
Build a team. What skills and experience does Amazon need to build a successful business? Amazon needs a team with a variety of skills, including product development, marketing, and sales.
Continuously improve. How will Amazon ensure that its business model is successful? Amazon will continuously improve its business model by listening to customer feedback and adapting to changes in the market.
The 8 steps in the business model are essential for any company that wants to be successful. By following these steps, companies can ensure that they are offering a valuable product or service to the right customers, and that they are able to make money.
In the case of Amazon, the company has clearly defined its value proposition, target market, and revenue streams.
Amazon's marketing plan is also effective, and the company has built a team with the skills and experience necessary to be successful. Finally, Amazon is committed to continuous improvement, which is why the company has been so successful over the years.
To know more about value click here
brainly.com/question/30760879
#SPJ11
Find the value of x.
8 20 36

Answers
Answer:
4.4
Step-by-step explanation:
do a ratio, so 8:36 = x:20
36/8=4.5
4.5x=20
x=4.4
jhjkhgfxdzfxcghjklhgfydfxcvbnklmoiuytfcgvb nmkljiouhytfrdfcgvhbjnkiuhygtfrhcgvhbjiou98y7tgvhmb
Answers
Answer:
uihuvbuh ufsghiusgu 8y39 8y3yy894y87y48jhfjhjbvhjjavjlh ailhli
Step-by-step explanation:
Write an exponential expression equivalent to 8^3 that has a base of 2.
Answers
The exponential expression equivalent to 8^3 that has a base of 2 is 2^9.
What is exponential expression?
Powers can simply be expressed in concise form using exponential expressions. The exponent shows how many times the base has been multiplied.
Applying the laws of indices,
The expression 8^3 can be written as,
8 x 8 x 8 = (2^3) x (2^3) x (2^3)
= 2^(3+3+3) ...{If a^m x a^n then a^(m+n) }
8 x 8 x 8 = 2^9
Therefore, the exponential expression equivalent to 8^3 that has a base of 2 is 2^9.
To know more about the exponential expressions, click on the link
https://brainly.com/question/28200743
#SPJ13
If (4 + 1) ( + 4) = 2 + + , what is the value of + + ?
Answers
CAN SOMEONE HELP ME WITH THIS QUESTION!!!

Answers
Answer:
E
Step-by-step explanation:
let a, b, c represent the number of students in 6th, 7th, 8th grade
ratio of students : teachers = 28 : 1
There are 82 teachers , so 28 × 82 = 2296 students
Then
a + b + c = 2296 , that is
828 + b + c = 2296 ( subtract 828 from both sides )
b + c = 1468 → E
express \sqrt{3} - \frac{2}{\sqrt{3} } \(\sqrt{3} - \frac{2}{\sqrt{3} }\)
Answers
\(\sqrt{3} - \frac{2}{\sqrt{3} } = \frac{3}{\sqrt{3} } - \frac{2}{\sqrt{3} } = \frac{1}{\sqrt{3} } = \frac{\sqrt{3} }{3}\)
ok done. thank to me :>
7. Sea level is at an elevation of O feet. The lowest elevation in Arizona is 72 2 points
feet. The lowest elevation in Louisiana is -68 feet. Which inequality is true?
72 < -68
-68 > 72
72 >-68
O
72 = -68

Answers
Answer:
The 3rd one down
72 > -68
Step-by-step explanation:
Subtract 1/8 minus 3/4
Answers
Answer: 5/8
Step-by-step explanation:
385 people get on an empty train at a station. At the first stop, 264 more people get on the train, and 89 people get off. There are no more stops until the train reaches it final destination, where everybody gets off the train.
How many people get off the train at the final destination?
Answers
385 people get on an empty train at a station. At the first stop, 264 more people get on the train, and 89 people get off. There are no more stops until the train reaches it final destination, where everybody gets off the train.
560 is the answer
560 people get off the train at the final destination.
Given that 385 people get on an empty train. At the first stop, 264 more people get on, and 89 people get off.
There are no more stops until the train reaches it final destination,
We need to find the number of the people who get off the train at the final destination.
To find out how many people get off the train at the final destination, let's break down the information given step by step.
385 people get on the empty train at the station.
At the first stop, 264 more people get on the train, bringing the total number of people on the train to 385 + 264 = 649.
Additionally, 89 people get off the train at the first stop.
After the first stop, there are no more stops until the final destination.
To find out how many people get off at the final destination, we need to subtract the number of people who got off at the first stop from the total number of people on the train after the first stop.
Total number of people on the train after the first stop = 649 (from step 2)
People who got off at the first stop = 89 (from step 3)
Number of people who get off at the final destination = Total number of people on the train after the first stop - People who got off at the first stop
Number of people who get off at the final destination = 649 - 89 = 560
Therefore, 560 people get off the train at the final destination.
Learn more about Arithmetical operations click;
https://brainly.com/question/30553381
#SPJ7