Answers
Answer:
50
Step-by-step explanation:
Think of line AE as a transversal. with DE and AB cutting across it. If we draw it out, looking at the picture, we can see that angles A and E correspond, meaning that angle A = angle E = 50

Related Questions
The volume of the right cone below is 2767 units³. Find the value of x.
Answers
The value of x is approximately 49.4 units.
What is volume ?
Volume is a measure of the amount of space occupied by a three-dimensional object. It is typically expressed in cubic units such as cubic meters, cubic centimeters, or cubic feet. Volume is a fundamental concept in mathematics and physics, and it is an important property for describing the size, capacity, or amount of material contained within an object.
Let's start by defining some variables:
r: radius of the cone
h: height of the cone
V: volume of the cone
A right cone has a circular base, and its volume can be calculated as follows:
V = (1/3) * π * r² * h
If the diameter of the base is 12 units, then the radius is half of that:
r = 6 units
We also know that the volume is 2767 units³, so we can write:
2767 = (1/3) * π * 6² * h
Simplifying:
h = (2767 * 3) / (π * 6²)
h ≈ 49.15 units
Now, we need to find the value of x. We can use the Pythagorean theorem to relate x, r, and h:
x² = r² + h²
Substituting the values we have:
x² = 6² + 49.15²
x ≈ 49.4 units
Therefore, the value of x is approximately 49.4 units.
In summary, we used the formula for the volume of a cone to relate the radius and height of the cone to its volume. Then, we used the Pythagorean theorem to relate the unknown value of x to the known values of r and h. Finally, we substituted the known values to find the approximate value of x.
To know more about volume visit:-
https://brainly.com/question/463363
#SPJ1
Your complete question is :-The volume of the right cone below is 2767 units³. Find the value of x if it's diameter is 12
using 250mililitres measuring cylinder, how many 250mililitres will give you 4litres
Answers
Answer:
sixteen 250 millilitres
Step-by-step explanation:
250 millimetres = 1/4 litre
4 litres = 16 one-fourth litres
PLZ MARK AS BRAINLIEST
what is 0.2 writen as a %
Answers
Which of the following points lie on a line that passes through the origin with a slope of −25? Select all that apply. Multiple select question. cross out A) (0, 0) cross out B) (1, −25) cross out C) (−2, 5) cross out D) (−1, 25) cross out E) (4, 10) cross out F) (−5, 2)
Answers
The points that will lie on the line will be (0, 0) , (1, - 25) , (- 1, 25).
What is the general equation of a straight line?The general equation of a straight line is : y = mx + c.
[m] is called slope and it tells the unit rate of change in [y] with respect to [x].
[c] is called the [y] - intercept.
We have some points that lie on a line that passes through the origin with a slope of −25.
The equation of a straight line that passes through the origin and has slope of -25 will be -
y = - 25x
The points that will lie on the line will be -
(0, 0) , (1, - 25) , (- 1, 25)
Therefore, the points that will lie on the line will be (0, 0) , (1, - 25) , (- 1, 25).
To solve more questions on Equations, Equation Modelling and Expressions visit the link below -
brainly.com/question/14441381
#SPJ1
Angle Terminology with Equations

Answers
Answer:
Please find attached pdf
Step-by-step explanation:
negative eight minus seven? (-8-7)
Answers
Answer:
-15 is the answer of this
Step-by-step explanation:
Rules in Algebra
Only need help 4 to 8 please Please help me my sister in the hospital and I don’t know how to do this type of homework I’m trying my best :( pray for my sister please

Answers
Answer:
I'm so sorry for ur sister
Consider the diagram.
Planes M and N intersect at line d. Lines a, b, and e are on plane M. Line a is vertical and forms a right angle with line d. Line b is diagonal and goes up and to the right. Line e is at the top of the plane and is close to being horizontal. Line c is on plane N and goes slightly up and to the right.
Lines a and d are
non-coplanar.
parallel.
perpendicular.
skew.
Answers
Answer:
perpindicular
Step-by-step explanation:
The line a and line d are perpendicular to each other.
What is a perpendicular lineA perpendicular line is a line that intersect another line at 90 degrees. Perpendicular lines are also called normal lines.
Constructing lines a and dAfter constructing the two lines; line a and line intersect or meet each other at 90 degrees to the horizontal.
Thus, we can conclude that the line a and line d are perpendicular to each other.
Learn more about perpendicular lines here: https://brainly.com/question/1202004
Can someone help me? I still don't understand this question.

Answers
\(f(x) = -6x^2 + 7x + 4\)
Step-by-step explanation:
For x = 1
\(a(1)^2 + b(1) + c = 5 \Rightarrow a + b + c = 5\) (1)
For x = -3,
\(a(-3)^2 + b(-3) + c = -71\)
\(\Rightarrow 9a - 3b + c = -71\) (2)
For x = 3,
\(a(3)^2 + b(3) + c = -29\)
\(\Rightarrow 9a + 3b + c = -29\) (3)
Let's add Eqn(2) and Eqn(3) together to eliminate b:
\(\Rightarrow 18a + 2c = -100\) (4)
Next, multiply Eqn(1) by 3 and then add to Eqn(2) to get
\(\Rightarrow 12a + 4c = -56\) (5)
Then we want to eliminate c by multiplying Eqn(4) by -2 and then adding to Eqn(5) and we will get
\(-24a = 144 \Rightarrow a = -6\)
Now that we have the value for a, we can use either Eqn(4) or Eqn(5) to solve for c and we will get
\(12(-6) + 4c = -56 \Rightarrow c = 4\)
Using the values of a and c on Eqn(1), we find that \(b = 7\) so therefore, our function f(x) has a form
\(f(x) = -6x^2 + 7x + 4\)
Given these four points: A(3, 3), B(−5, 7), C(2, 11), and D(9, −2), find the coordinates of the midpoint of line segments AB and CD.
Answers
Midpoint formula: (x1 + x2)/2 , (y1 + y2)/2
Midpoint AB = (3 +-5)/2, (3 + 7)/2 = -2/2 , 10/2 = (-1,5)
Midpoint CD = (2 +9)/2, (11 + -2)/2 = (11/2,9/2)
how much cm³ is it the cilinder?

Answers
Answer:
one because it is cilinder
Answer:
3619.11 cm^3
Step-by-step explanation:
Volume of a cylinder = area of end * height
= pi r^2 * height
= pi (6)^2 * 32 cm^3
= 36 pi * 32 = 3619.11 cm^3
Find the distance of AB
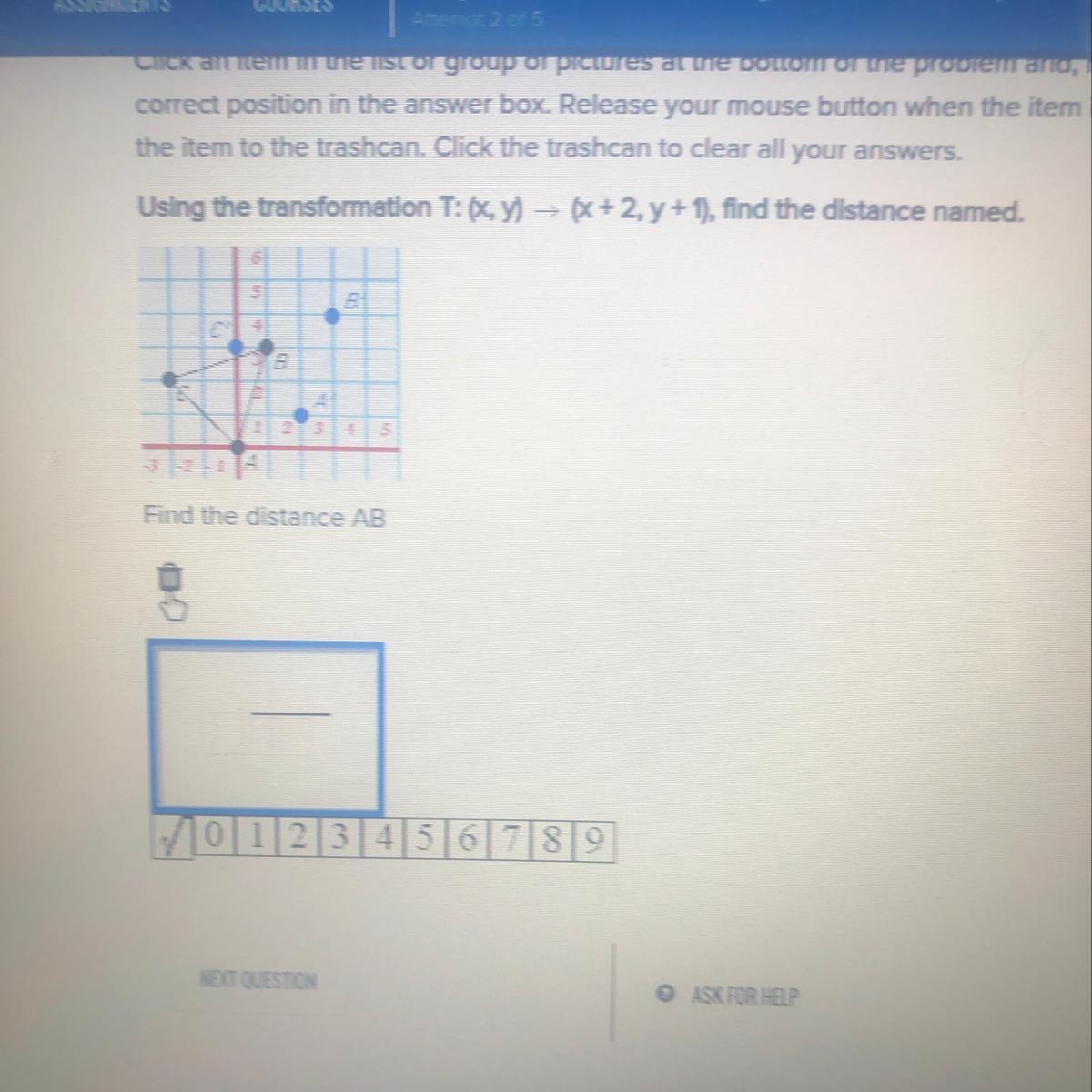
Answers
Answer:
d = \(\sqrt{10\\\)
Step-by-step explanation:
Use the distance formula: d = \(\sqrt{(x2 - x1)^{2} + (y2 - y1)^{2}\)
A (0, 0)
B ( 1, 3)
d = \(\sqrt{(1 - 0)^{2} + (3 - 0)^{2}\)
d = \(\sqrt{(1)^{2} + (3)^{2}\)
d = \(\sqrt{1 + 9\)
d = \(\sqrt{10\)
1. Prove ~ (Pvq) <=> (~P^~9).
Algebra of propositional variables
2. P^ q = q^q
P v q = q v p
show that both are commutative
Answers
Based on the information, both ∧ (conjunction) and ∨ (disjunction) satisfy the commutative property.
How to explain the commutative property.It should be noted that to prove the commutativity of the logical connectives ∧ (conjunction) and ∨ (disjunction), we need to show that they satisfy the commutative property
From the truth table, both P ∧ Q and Q ∧ P have the same truth values for all combinations of truth values of P and Q. Therefore, we can conclude that P ∧ Q ≡ Q ∧ P, and ∧ (conjunction) is commutative.
In order to prove P ∨ Q ≡ Q ∨ P, we construct a truth table for both expressions. Both P ∨ Q and Q ∨ P have the same truth values for all combinations of truth values of P and Q. Therefore, we can conclude that P ∨ Q ≡ Q ∨ P, and ∨ (disjunction) is commutative.
Hence, both ∧ (conjunction) and ∨ (disjunction) satisfy the commutative property.
Learn more about commutative property. on
https://brainly.com/question/778086
#SPJ1
From least to greatest, What are the x–coordinates of the three points where the graphs of the equations intersect? If approximate, enter values to the hundredths.
,
,
Answers
The x-coordinates where the graphs of the equations intersect are x = -1 and x = 3
How to determine the x-coordinates where the graphs of the equations intersect?From the question, we have the following parameters that can be used in our computation:
y = 2x
y = x² - 3
The x-coordinates where the graphs of the equations intersect is when both equations are equal
So, we have
x² - 3 = 2x
Rewrite the equation as
x² - 2x - 3 = 0
When the equation is factored, we have
(x + 1)(x - 3) = 0
So, we have
x = -1 and x = 3
Hence, the x-coordinates are x = -1 and x = 3
Read more about equations at
https://brainly.com/question/148035
#SPJ1
Question
From least to greatest, What are the x–coordinates of the three points where the graphs of the equations intersect? If approximate, enter values to the hundredths.
y = 2x
y = x² - 3
What is the answer ? And explain

Answers
Answer:
The equation of the line is y = 2x - 6
Step-by-step explanation:
Put the equation into the point-slope formula (Below). You'll get y - 4 = 2 * (x - 5), which is equal to y - 4 = 2x - 10. You add 4 on both sides and then get y = 2x - 6.
Point-Slope formula:
y - y coordinate = slope * (x - x coordinate)
Y coordinate: 4
X coordinate: 5
Slope (m) = 2
Estimate the perimeter of the figure to the nearest whole number.
perimeter: about units
Answers
you would have to give us the shape to figure it out
Factor the following trinomials.
\(x^{2} - 2x -1\)
\(x^{2} - 3x+1\)
Answers
Answer:
maybe you have to add more on to thj side
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

In a company, 85% of the workers are men. If 360 people work for the company who aren't men, how many workers are there in all? Use pencil and paper. Show two different ways that you can solve this problem.
Answers
If 85% are men, then (100 - 85), 15% are not men
so, 15% are not men which means that 15% are 360 = 15% of x = 360
(x = total no. of workers)
so, x = 360 × \(\frac{100}{15}\) = 2400
The total number of people = 2400
( sorry I didn't use pencil...)
Which of the following is the graph of f(x) = 5 cos (2x)? Select one: a. graph with points 0, 5 and pi over 4, 0 and pi over 2, negative 5 and 3 pi over 4, 0 and pi, 5 b. graph with points at 0, 0 and pi over 4, negative 3 and pi over 2, 0 and 3 pi over 4, 3 and pi, 0 c. graph with points 0, negative 5 and pi over 4, 0 and pi over 2, 5 and 3 pi over 4, 0 and pi, negative 5 d. graph with points at 0, 5 and pi over 4, 2 and pi over 2, negative 1 and 3 pi over 4, 2 and pi, 5
Answers
The required graph has been attached below that represents the function f(x) = 5 cos (2x).
The graph of the function f(x) = 5 cos(2x) is a periodic function that oscillates between its maximum and minimum values as x changes.
Specifically, the function is a cosine function with amplitude 5 and period π, since the coefficient of x is 2 in the argument of the cosine function.
The graph of the function f(x) = 5 cos(2x) has a maximum value of 5 when cos(2x) = 1 (i.e., at 2x = 0 + 2πk, where k is an integer), and a minimum value of -5 when cos(2x) = -1 (i.e., at 2x = π + 2πk, where k is an integer).
Thus, the graph has been attached below that represents the given function.
Learn more about Trigonometric functions here:
brainly.com/question/6904750
#SPJ1

Identify the domain of the function shown in the graph

Answers
Answer:
D. -5 ≤ x ≤5
Step-by-step explanation:
Domain is the set of x-values that can be inputted into function f(x).
We see from the graph that our x-values span from -5 to 5. Since both are closed dots, they are included in our domain:
[-5, 5]
or
-5 ≤ x ≤ 5
4. There are 36 units in a case. You have 90 loose units of stock in the store. The store manager has requested a stock count in CASES. How many cases of stock will 90 units fill? CALCULATION:
Answers
There are 36 pieces in one case. The store has 90 loose storage units. The store manager requested an inventory count where 2.5 units would fill her 90 units.
What is the inventory process like?Typically, this process involves the retailer (or team of employees) walking through the retailer's warehouse and storefront, counting each item. Information is captured manually using pen and paper or electronically using a mobile device.
Create a storage location map showing each shelf, bin, drawer, receiving dock, and return area. Place geographic divisions, not product lines, between each storage area. Let's start counting! After each counter completes a certain range, allow a manager or someone else to check the count.
90/36 = 2.5
To learn more about stock visit:
brainly.com/question/25818989
#SPJ1
HELP! I WILL AMKE YOU BRAINLIEST BC THIS IS DUE TODAY!!!

Answers
Answer: 27.3
Step-by-step explanation:
I took the outcomes of the Aces from the trial and found the average and the answer I got was 27.3%
Hope this helps.
A bag contains 16 cards numbered 1 through 16. A card is randomly chosen from the bag. What is the probability that the card has a multiet of 3 on it?write your answer as a fraction insimplest form.
Answers
Answer:
Given that,
A bag contains 16 cards numbered 1 through 16
To find the probability that the card has a multiple of 3 on it
Let A be the event of the probability that the card has a multiple of 3 on it
we get,
A={3,6,9,12,15}
Number of possibliles of the event A n(A)=5
Total number of possibilities n(S)=16
Probability that the card has a multiple of 3 is,
\(=\frac{n(A)}{n(S)}\)Substitute the values we get,
\(=\frac{5}{16}\)Answer is: Probability that the card has a multiple of 3 is 5/16.
ABC~A'B'C'. Their scale factor is 7:9. If the perimeter of smaller ABC is 42, then the
perimeter of A'B'C' is.
Pls hurry!!
Answers
Answer:
54
Step-by-step explanation:
ratio is 7:9
7=42
9=?
9×42÷7
You select a family with three children. If M represents a male child and F a female child, the set of equally likely outcomes for the children's genders is shown below. Find the probability of selecting a family with at least three male children.
{MMM, MMF, MFM, MFF,
Answers
The probability to select a family with atleast three male children is only 1/8.
What is Probability?A probability is a number that reflects the chance or likelihood that a particular event will occur.
First, you have the sample of the children.
We know that the family with 3 children, can have the sample space as given {MMM,MMF,MFM,FMM,FFM,FMF, FFF}
MMM: 3 Males
MMF: 2 males, 1 female
MFF: 1 male, 2 females
MFM: 2 males, 1 female (different order)
FMM: 1 female, 2 males
FFM: 2 females, 1 male
FMF: 2 females, 1 male
FFF: 3 females
If we count all of these possibilities, we have 8 possible cases of family with the childrens.
In only one of them, we have atleast three males , which is the first one
Therefore, the probability to select a family with atleast three male children is only 1/8.
To learn more on Probability click:
https://brainly.com/question/16722133
#SPJ1
Translate the verbal phrase
:- "twice of number y Increased by five" into mathematical expression. PLS HELP!

Answers
\(\bold\purple{Hopeithelps}\)
\(\bold{Study}\)\(\bold{Well}\)~
Dena is buying wallpaper. It costs $8.79 per meter. She needs 120 feet. How much will the wallpaper cost? Round to the nearest half dollar.
Answers
Answer:
321.50 dollars.
Step-by-step explanation:
Dena is buying wallpaper. It costs $8.79 per meter. She needs 120 feet. How much will the wallpaper cost? Round to the nearest half dollar.
This is a tricky math problem that requires some conversions and calculations. First, we need to convert feet to meters, because Dena lives in a country that uses the metric system. According to the search results , one foot is equal to 0.3048 meters. So, 120 feet is equal to 120 x 0.3048 = 36.576 meters.
Next, we need to multiply the length of the wallpaper by the price per meter to get the total cost. The total cost is 36.576 x 8.79 = $321.38.
Finally, we need to round the total cost to the nearest half dollar. This means we need to look at the cents part of the cost and see if it is closer to 0, 50 or 100. In this case, 38 cents is closer to 50 than to 0 or 100, so we round up the cost to $321.50.
Therefore, Dena will have to pay $321.50 for the wallpaper. That's a lot of money for some paper that will probably peel off in a few years! Maybe she should consider painting her walls instead.
construct a 33 matrix a, with nonzero entries, and a vector b in such that b is not in the set spanned by the columns of a.
Answers
Let a be a 33 matrix with nonzero entries, and b be a vector with elements that are not linear combinations of the columns of a. Then b is not in the set spanned by the columns of a.
Let's construct a 33 matrix a with nonzero entries. We can construct this matrix by deciding on 33 elements, each of which is not equal to zero, and arranging them into 33 columns and rows with each column and row having one element. Next, we can create a vector b with elements that are not linear combinations of the columns of a. This can be done by deciding on 33 elements for the vector b and ensure that none of the elements of b are linear combinations of the elements of the matrix a. Finally, we can test whether b is in the set spanned by the columns of a. To do this, we can take each column of a and check if any of the elements in b can be expressed as a linear combination of the elements in that column. If any of the elements in b can be expressed as a linear combination of the elements in any of the columns of a, then b is in the set spanned by the columns of a. Otherwise, b is not in the set spanned by the columns of a.
Learn more about matrix here
https://brainly.com/question/29132693
#SPJ4
Solve for x and graph the solution on the number line below
9 > x − 3

Answers
Answer:
Step-by-step explanation:
Solve for x and graph the solution on the number line below
9 > x − 3
add 3 to both sides:
9 + 3 > x − 3 + 3
12 > x
so: (12, ∞)
___-4__-2__0__2__4__6__8__10__(12__13__`14__16______
