Use the Taylor series for f(x)= 3√x, centered at x = 8, to approximate 3√16 to four decimal places. 3√16 = ____ (Type an integer or a decimal.)

A linear equation modeling Robert's weight-loss situation is x = 205 + 2y.

A linear equation is an equation modeling a straight-line relationship between two variables, for example, x and y.

The weight lost per week = 2 pounds

The number of weeks weight was lost, y = 6 weeks

Robert's weight after 6 weeks of losing 2 pounds weekly = 205

Let x = Robert's weight before the weight-loss program

x = 205 + 2y

x = 205 + 2(6)

x = 205 + 12

x = 217

Learn more about linear equations at https://brainly.com/question/28732353.

#SPJ1

Answer:

5x +2

Step-by-step explanation:

6x+3−(x+1) =

Distribute the minus sign

6x +3 -x -1

5x +2

Answer:

\(5x + 2\)

Step-by-step explanation:

\(6x + 3 - (x + 1) \\ 6x + 3 - x - 1 \\ = 5x + 2\)

hope this helps

brainliest appreciated

good luck! have a nice day!

false. range of \( \cos^{-1}(x)\) is $[0,\pi]$

The conditional expectation E[Y|X=2] is 11, and the variance of Y, var(Y), is 24, given the linear relationship Y = 15 - 2X and a variance of 6 for X.

The conditional expectation E[Y|X=2] represents the expected value of Y when X takes on the value 2.

Given the linear relationship Y = 15 - 2X, we can substitute X = 2 into the equation to find Y:

Y = 15 - 2(2) = 15 - 4 = 11

Therefore, the conditional expectation E[ Y|X=2] is equal to 11.

To calculate the variance of Y, var(Y), we can use the property that if X and Y are linearly related, then var(Y) = b^2 * var(X), where b is the coefficient of X in the linear relationship.

In this case, b = -2, and the variance of X is given as 6.

var(Y) = (-2)^2 * 6 = 4 * 6 = 24

Therefore, the variance of Y, var(Y), is equal to 24.

To learn more about linear , click here:

brainly.com/question/31510526

#SPJ1

The expression that only uses multiplication and that is equivalent to x reduced by 1/8 of x is: x * (1 - 1/8).

An expression in mathematics is a combination of numbers, variables, and operations that represent a value or set of values.

The expression calculates the reduction of x by 1/8 of x by subtracting 1/8 of x from x, which is x * 1/8. By subtracting this from x, the expression calculates x reduced by 1/8 of x. The expression that only uses multiplication and that is equivalent to x reduced by 1/8 of x is:

x * (1 - 1/8).

To learn more about expression here:

https://brainly.com/question/14083225

#SPJ4

Answer:

\(f(x)=x^2-11x+30\)

Step-by-step explanation:

The factored form of a quadratic is given by:

\(f(x)=a(x-p)(x-q)\)

Where p and q are the zeros, and a is the leading coefficient.

The quadratic relation has zeros of 5 and 6, and it has a y-intercept of 30.

Since the zeros are 5 and 6, p and q are 5 and 6. Thus:

\(f(x)=a(x-5)(x-6)\)

The y-intercept is 30. In other words, when x = 0, f(x) = 30:

\(30=a(0-5)(0-6)\)

Solve for a:

\(30=a(-5)(-6)\Rightarrow 30=30a\Rightarrow a=1\)

Therefore, our quadratic in factored form is:

\(f(x)=(x-5)(x-6)\)

To find the standard form, expand:

\(\begin{aligned} f(x)&=(x-5)(x-6)\\&= (x-5)x+(x-5)(-6)\\&=(x^2-5x)+(-6x+30)\\&=x^2-11x+30\end{aligned}\)

A) The inverse of the function y = 3√x is given by y =\(x^3/27.\)

B) the inverse of the function y = \(-(0.4)∛x - 2 is given by y = -15.625(x + 2)^3.\)

To find the inverse of the function y = 3√x, we need to switch the roles of x and y and solve for y.

Let's start by rewriting the equation with y as the input and x as the output:

x = 3√y

To find the inverse, we need to isolate y. Let's cube both sides of the equation to eliminate the cube root:

\(x^3 = (3√y)^3x^3 = 3^3 * √y^3x^3 = 27y\)

Now, divide both sides of the equation by 27 to solve for y:

\(y = x^3/27\)

Therefore, the inverse of the function y = 3√x is given by y = x^3/27.

For the second function, y = -(0.4)∛x - 2, we can follow the same process to find its inverse.

Let's switch the roles of x and y:

\(x = -(0.4)∛y - 2\)

To isolate y, we first add 2 to both sides:

\(x + 2 = -(0.4)∛y\)

Next, divide both sides by -0.4 to solve for ∛y:

-2.5(x + 2) = ∛y

Cube both sides to eliminate the cube root:

\(-2.5^3(x + 2)^3 = (∛y)^3-15.625(x + 2)^3 = y\)

Therefore, the inverse of the function y = \(-(0.4)∛x - 2 is given by y = -15.625(x + 2)^3.\)

It's important to note that the domain and range of the original functions may restrict the domain and range of their inverses.

for more such question on inverse visit

https://brainly.com/question/3831584

#SPJ8

Answer:

The radius is 9.28 inches.

Step-by-step explanation:

Since there are 7 Move Ahead zones, and 3 Go Backwards zones on the spinner, there must be 2 other zones (the Freeze! +Bonus pts)

2 out of 12 zones are Freeze! +Bonus pts. That is 1/6 of the spinner. They said the area of the the Freeze!+Bonus pts is 45.1 inches squared.

45.1 × 6

= 270.6

The entire spinner has the area 270.6

The area of a circle is:

A = pi•r^2

We are looking for r. Thats the radius they asked for in the question.

270.6 = pi•r^2

pi is a number, I'm using the pi button on the calculator bc it is most exact.

270.6 = pi•r^2

Divide both sides by pi.

86.134655 = r^2

square root both sides.

9.28 = r

The radius is 9.28 inches.

The height of Reggie’s dog in feet and inches are,

⇒ 2.46 feet

A measurement unit is a standard quality used to express a physical quantity. Also it refers to the comparison between the unknown quantity with the known quantity.

Given that;

Reggie’s dog is 75 centimeters tall.

We know that;

1 cm = 0 feet 0.394 inch

       = 0.0328 feet

Hence, The height of Reggie’s dog in feet and inches are,

⇒ 75 cm = 75 x 0.0328 feet

               = 2.46 feet

Thus, The height of Reggie’s dog in feet and inches are,

⇒ 2.46 feet

Learn more about the measurement unit visit:

https://brainly.com/question/777464

#SPJ9

The total area of the diamond is 19.5 square cm.

The total area of the diamond can be calculated by finding the area of the trapezoid and triangle separately and adding them together.

The area of the trapezoid can be calculated using the formula for the area of a trapezoid:

Area = (base1 + base2) / 2 × height

Where base1 and base2 are the lengths of the parallel sides and height is the distance between the parallel sides. In this case, base1 and base2 are both 4 cm, and height is 2 cm, so:

Area = (4 + 4) / 2 × 2 = 4 × 2 = 8 square cm

The area of the triangle can be calculated using the formula for the area of a triangle:

Area = (base × height) / 2

In this case, the base is 4 cm, and the height is 5.75 cm, so:

Area = (4 × 5.75) / 2 = 11.5 square cm

Adding the area of the trapezoid and triangle together:

Area = 8 + 11.5 = 19.5 square cm

So the total area of the diamond is 19.5 square cm.

To know more about trapezoid, here

https://brainly.com/question/28088913

#SPJ4

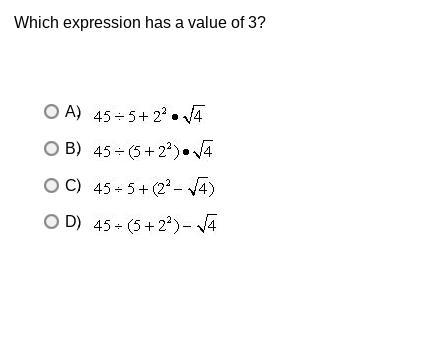
Answer:

Step-by-step explanation:

Use SOH CAH TOA to recall how the trig functions fit on a triangle

SOH: Sin(Ф)= Opp / Hyp

CAH: Cos(Ф)= Adj / Hyp

TOA: Tan(Ф) = Opp / Adj

since we know the angle and the Hyp, and want to find the opp, use

SOH

Sin(41) = Opp / 111

111*Sin(41) = Opp

72.82255... = Opp

x = 72.8  ( rounded to nearest 10th )

ask if you want more explanation. :)

Answer:

9

Step-by-step explanation:

2(5)-(1)

10-1

9

Answer:

7.58333333333

The light fixtures will make approximately 0.914 swings per second during a minor earthquake in San Francisco.

To determine the frequency of the swings per second for the light fixtures, we need to use the formula for the period of a pendulum, which is T = 2π√(L/g), where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity.

In this case, the length of the pendulum is given as 1.50 m, and the mass of the bulb is given as 2.35 kg. We can assume that the shade and cord add negligible mass to the system. The acceleration due to gravity is approximately 9.8 m/s^2.

Plugging in the values, we get:

T = 2π√(1.50/9.8)

T ≈ 1.093 seconds

The frequency of the swings per second is the reciprocal of the period, so:

f = 1/T

f ≈ 0.914 Hz

It's important to note that this is an approximation, and the actual frequency may vary depending on factors such as the amplitude of the oscillations and the specific characteristics of the earthquake.

To learn more about light fixtures click on,

https://brainly.com/question/24462367

#SPJ4

Writing linear equations given two points can be a useful skill when graphing linear equations.

To learn more about linear equation refer to:

https://brainly.com/question/2030026

#SPJ1

The probability distribution of X is given as P(x) = 1/4m, 2/4m, 3/4m, and 4/4m for values of x = 1, 2, 3, and 4 respectively.

To find m, we can use the fact that the sum of all probabilities in a distribution must equal 1.

So, we can set up the equation:

1/4m + 2/4m + 3/4m + 4/4m = 1

Simplifying the equation gives us:

10/4m = 1

Multiplying both sides of the equation by 4m gives us:

10 = 4m

Finally, we can solve for m by dividing both sides of the equation by 4:

m = 10/4

m = 2.5

As a decimal rounded to one decimal place, m = 2.5.

So, the probability distribution of X is P(x) = 1/10, 2/10, 3/10, and 4/10 for values of x = 1, 2, 3, and 4 respectively.

Learn more about probability distribution

brainly.com/question/14210034

#SPJ11

Answer:

  2) 162°, 72°, 108°

  3) 144°, 54°, 126°

Step-by-step explanation:

1) Multiply the equation by 2sin(θ) to get an equation that looks like ...

   sin(θ) = <some numerical expression>

Use your knowledge of the sines of special angles to find two angles that have this sine value. (The attached table along with the relations discussed below will get you there.)

____

2, 3) You need to review the meaning of "supplement".

It is true that ...

  sin(θ) = sin(θ+360°),

but it is also true that ...

  sin(θ) = sin(180°-θ) . . . . the supplement of the angle

This latter relation is the one applicable to this question.

__

Similarly, it is true that ...

  cos(θ) = -cos(θ+180°),

but it is also true that ...

  cos(θ) = -cos(180°-θ) . . . . the supplement of the angle

As above, it is this latter relation that applies to problems 2 and 3.

The maximum profit is approximately 229.4534.

How to maximize firm's profit?

To solve the problem of profit maximization, we need to find the quantity of output that maximizes the firm's profit. We can do this by finding the quantity at which marginal revenue equals marginal cost.

Given:

Demand: Q = 300 - 2P

Total cost: C(Q) = 75Q^2

To find the marginal revenue, we need to differentiate the demand equation with respect to quantity (Q):

MR = d(Q) / dQ

Differentiating the demand equation, we get:

MR = 300 - 4Q

To find the marginal cost, we need to differentiate the total cost equation with respect to quantity (Q):

MC = d(C(Q)) / dQ

Differentiating the total cost equation, we get:

MC = 150Q

Now, we set MR equal to MC and solve for the quantity (Q) that maximizes profit:

300 - 4Q = 150Q

Combining like terms:

300 = 154Q

Dividing both sides by 154:

Q = 300 / 154

Simplifying:

Q ≈ 1.9481

So, the quantity that maximizes profit is approximately 1.9481.

To find the corresponding price, we substitute the quantity back into the demand equation:

P = 300 - 2Q

P = 300 - 2(1.9481)

P ≈ 296.1038

Therefore, the price that maximizes profit is approximately 296.1038.

To calculate the maximum profit, we substitute the quantity and price into the profit equation:

Profit = (P - MC) * Q

Profit = (296.1038 - 150(1.9481)) * 1.9481

Profit ≈ 229.4534

Therefore, the maximum profit is approximately 229.4534.

Learn more about profit maximization

brainly.com/question/30072001

#SPJ11

The internal shear for 0≤x≤4m in terms of x is given by the equation V(x) = -wx, where w is the distributed load in N/m.

Internal shear refers to the shear force acting within a section of a beam. In this case, we are given a beam with a distributed load w and we need to express the internal shear in terms of x for 0≤x≤4m. To do this, we can use the equation for distributed load:
w = dW/dx
where W is the total load on the beam and dW/dx is the rate of change of load with respect to distance. Integrating this equation.


The equation for distributed load is:
w = dW/dx
where W is the total load on the beam and dW/dx is the rate of change of load with respect to distance. Integrating this equation, we get:
W(x) = ∫0x w dx
Substituting the value of w from the given equation, we get:
W(x) = ∫0x (-wx) dx = -wx^2/2
The negative sign indicates that the load is acting in the opposite direction to the positive x-axis. This means that the total load on the beam decreases as we move from the left end towards the right end.
The internal shear V(x) at a distance x from the left end of the beam is given by the derivative of W(x) with respect to x:
V(x) = dW/dx = -wx
Therefore, the internal shear for 0≤x≤4m in terms of x is given by the equation V(x) = -wx, where w is the distributed load in N/m.

To know more about equation visit :-

https://brainly.com/question/29657983

#SPJ11

Answer:

4,098734

Step-by-step explanation:

Answer:

b<1/5

Step-by-step explanation:

10b+7<5b+8

     -7        -7

10b < 5b+1

-5b         -5b

5b < 1

/5     /5

b < 1/5

The value of the test statistic for the given hypotheses is -2.6087. To calculate the test statistic, we can use the formula for a one-sample z-test:

z = (x - μ) / (σ / \(\sqrt{(n)}\))

where x is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.

In this case, the sample mean (x) is 132, the population mean (μ) is 120, the population standard deviation (σ) is 46, and the sample size (n) is 50.

Plugging these values into the formula, we have:

z = (132 - 120) / (46 / sqrt(50))

 = 12 / (46 / 7.0711)

 = 12 / 6.5203

 = 1.8387

Since the alternative hypothesis is μ ≠ 120, we are conducting a two-tailed test. The critical value for a two-tailed test with a significance level of 0.05 is ±1.96.

Comparing the test statistic (1.8387) with the critical value, we find that the test statistic does not fall outside the critical region. Therefore, we do not reject the null hypothesis. This means there is not enough evidence to conclude that the population mean is significantly different from 120 based on the given sample.

To leran more about test statistic, refer:-

https://brainly.com/question/31746962

#SPJ11

Answer:

Step-by-step explanation:

1. D 2. B 3. D

Answer: -0.58

Divide 5.8 y 100 y te da 0.058 despues lo multiplicas con (-10) y te da -0.58

Answer:q = 6+43r/9

Step-by-step explanation:

Assuming R=9q-43r-6 is what you meant
R+6 = 9q - 43r
R + 6 + 43r = 9q
q = 6+43r/9

The square root function involves the square root symbol √ which is  mostly read as "square root of", the rule says that the square root of a number 'x' is a number 'y' such that y² = x.

We know that the square root of a number can be either positive or negative, but while defining the square root function, we restrict its range to be the set of all positive real numbers and hence making all square roots possible to be positive.

If the range for the square root of a number is set to be positive as well as negative it wont be a function that is why there is a restriction to the range of this set allowing only positive real numbers.

To learn more about square root, click here:

brainly.com/question/29286039

#SPJ4

Solution:

The volume of the cases in 2001 is given below as

The percentage increase from 2000 is given below as

The exponential function is given below as

By substituting the values, we will have

Hence,

The final answer is YES, THE EXPONENTIAL MODEL FUNCTION IS APPROPRIATE

Therefore,

The exponential model after y years will be