Use the graphing tool to find the local minimum and thelocal maximum for the given function.Over the interval (-3,-1], the local minimum is2010Over the interval [-1.0], the local maximum is4-22Over the interval [0, 3], the local minimum is-10-20-30
Answers
Problem
Solution
Over the interval (-3,-1], the local minimum is:
0
Over the interval [-1.0], the local maximum is:
5
Over the interval [0, 3], the local minimum is:
-32

Related Questions
Find the missing digit for the following bank identification numbers:
71100139█
321000█56
Answers
Answer:
711001392
321000759
Step-by-step explanation:
hope it helps ^o^
Type such digits that's are correlated to both numbers but they are not present in both rather than present in one.
They can be 2 and 7 or 5 and 9
711001392321000756You can write other one also
how to write 720,080 in expanded form with exponents?
Answers
The number may be written as:
720,080
\(= \frac{720,080}{100,000} X 100,000\)
\(=7.2008 X 10^5\)
Answer: 7.2008 x 10⁵
Please give me brainlest ;(
2x2 - 32 = 0 solve in factored form
Answers
Answer:
2(x - 4)(x + 4) = 0
x = {-4, 4}
Step-by-step explanation:
2x² - 32 = 0
factor out 2
2(x² - 16) = 0
This is a difference of squares
Factor
2(x - 4)(x + 4) = 0
x = {-4, 4}
Answer:
Step-by-step explanation:
Hope it helps you!!
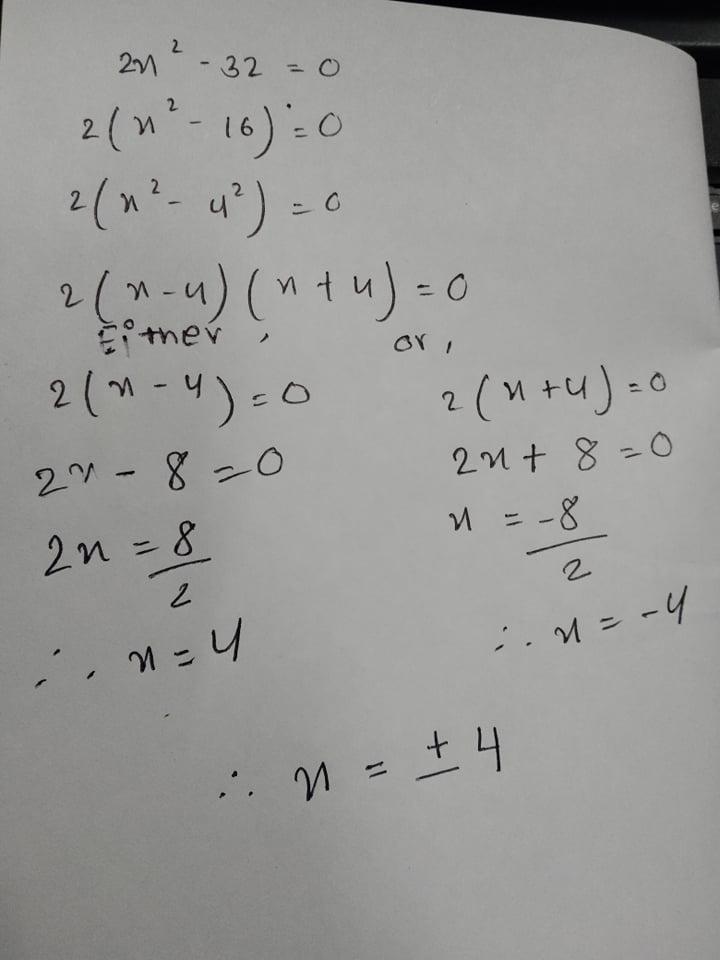
A scuba diver has a rope connecting the dive boat to an anchor on the ocean floor. The rope is 13ft long. The water is 5ft deep. How far is the anchor from a point directly below the boat?
Answers
Answer:
The anchor is 12 feet far from the point directly below the boat.
Step-by-step explanation:
Given that:
Length of rope connecting the dive boat to an anchor = 13 feet
Depth of water = 5 feet
Here,
The rope connecting the dive boat to the anchor will serve as hypotenuse of a right angle triangle, depth of water will be the height of triangle and distance from anchor to point directly below the boat will be base of triangle.
Using Pythagorean theorem;
\(a^2+b^2=c^2\)
a = 5 , c = 13
\((5)^2+b^2=(13)^2\\25+b^2=169\\b^2=169-25\\b^2=144\)
Taking square root on both sides
\(\sqrt{b^2} =\sqrt{144}\\b=12\)
Hence,
The anchor is 12 feet far from the point directly below the boat.
find the mean absolute deviation {3,4,5,6,7}
Answers
Answer:
it's 1.2
Step-by-step explanation:
there's also a calculator online for mad
Determine if the line segment YX is tangent to circle Z. 30 points

Answers
Answer:
XY is tangent to circle Z
Step-by-step explanation:
You want to know if segment XY, measuring 3.6 units, is tangent to circle Z at point X. Segment YZ has length 1.8 units outside the circle, which has radius 2.7 units.
Pythagorean relationIf the triangle XYZ is a right triangle, then we have ...
XY² +XZ² = YZ²
3.6² +2.7² = (1.8 +2.7)²
12.96 +7.29 = 20.25 . . . . . true
Segment XY is a tangent.
Secant relationIf segment YZ is extended across the circle, the lengths of the segments from Y to the circle intersection points are 1.8 and (1.8 +2·2.7) = 7.2. The relation between the secant and the "tangent" will be ...
3.6² = (1.8)(7.2) . . . . . true
This means XY is a tangent.
A rectangular block has a length of 8 inches, a width of 3.5 inches, and a height of 2 inches. Four blocks are stacked to create a tower. What is the volume of the tower? O A. 56 in 3 O B. 140 in 3 O C. 280 in O D. 336 in
Answers
The volume of the tower is 224 in³, which is not listed among the given options.
To find the volume of the rectangular block, we need to multiply its length, width, and height. Therefore, the volume of the single block is:
8 x 3.5 x 2 = 56 cubic inches.
Since we are stacking four blocks to create a tower, we need to multiply the volume of a single block by 4.
Thus, the volume of the tower is:
56 x 4 = 224 cubic inches.
The volume of a rectangular block can be found using the formula,
V = length × width × height.
In this case, the length is 8 inches, the width is 3.5 inches, and the height is 2 inches.
V = 8 × 3.5 × 2 V
= 28 × 2 V
= 56 in³
Now that we know the volume of one block, we can find the volume of the tower created by stacking four blocks. Tower volume = block volume × number of blocks Tower volume = 56 in³ × 4 Tower volume = 224 in³
For similar question on volume:
https://brainly.com/question/1578538
#SPJ11
Consider randomly selecting a student who is among the 12,000 registered for the current semester in a college. Let X be the number of courses the selected student is taking, and suppose that X has the following probability distribution: x 1 2 3 4 5 6 7 f(x) 0.01 0.02 0.12 0.25 0.42 0.16 0.02 a. Find the cdf of X. b. Find the expected number of courses a student is taking this semester. c. Find the variance of X. d. Find the third quartile of this distribution.
Answers
Answer:
a)
\(P(X \leq 1) = 0.01\)
\(P(X \leq 2) = 0.03\)
\(P(X \leq 3) = 0.15\)
\(P(X \leq 4) = 0.40\)
\(P(X \leq 5) = 0.82\)
\(P(X \leq 6) = 0.98\)
\(P(X \leq 7) = 1\)
b)
4.61
c) 1.1579
d) 5 is the third quartile of this distribution.
Step-by-step explanation:
We are given the following discrete distribution:
\(P(X = 1) = 0.01\)
\(P(X = 2) = 0.02\)
\(P(X = 3) = 0.12\)
\(P(X = 4) = 0.25\)
\(P(X = 5) = 0.42\)
\(P(X = 6) = 0.16\)
\(P(X = 7) = 0.02\)
a. Find the cdf of X.
Probability of X being less of equal to x. Than
\(P(X \leq 1) = P(X = 1) = 0.01\)
\(P(X \leq 2) = P(X = 1) + P(X = 2) = 0.01 + 0.02 = 0.03\)
\(P(X \leq 3) = P(X \leq 2) + P(X = 3) = 0.03 + 0.12 = 0.15\)
\(P(X \leq 4) = P(X \leq 3) + P(X = 4) = 0.15 + 0.25 = 0.40\)
\(P(X \leq 5) = P(X \leq 4) + P(X = 5) = 0.4 + 0.42 = 0.82\)
\(P(X \leq 6) = P(X \leq 5) + P(X = 6) = 0.82 + 0.16 = 0.98\)
\(P(X \leq 7) = P(X \leq 6) + P(X = 7) = 0.98 + 0.02 = 1\)
b. Find the expected number of courses a student is taking this semester.
Multiplication of every outcome by its probability.
\(E = 0.01*1 + 0.02*2 + 0.12*3 + 0.25*4 + 0.42*5 + 0.16*6 + 0.02*7 = 4.61\)
c. Find the variance of X.
Multiplication of the squared subtraction of each value and the mean, multiplied by its probability. So
\(V = 0.01*(1-4.61)^2 + 0.02*(2-4.61)^2 + 0.12*(3-4.61)^2 + 0.25*(4-4.61)^2 + 0.42*(5-4.61)^2 + 0.16*(6-4.61)^2 + 0.02*(7-4.61)^2 = 1.1579\)
d. Find the third quartile of this distribution.
100*(3/4) = 75th percentile
The cdf passes 0.75 when X = 5, so 5 is the third quartile of this distribution.
In a box there are 9 action, 12 Disney, 8 horror, 11 mystery and 4 SciFi movies. What is the probability of selecting horror or mystery movie?
Round your answer to the nearest thousandth. For example: 0.500 or 0.999
Answers
======================================================
Explanation:
There are 8+11 = 19 movies that are either horror or mystery.
This is out of 9+12+8+11+4 = 44 movies total.
Divide the two sums to get 19/44 = 0.43181818181818 approximately.
This rounds to 0.432
There's roughly a 43.2% chance of picking a horror or mystery movie.
HI HELLO ITS MATH I. NEED HELP

Answers
Formula for slant height:
\(l = \sqrt{ {r}^{2} + {h}^{2} } \)
We dont have height so we will find it with the help of area
\( \sf \: area = \pi {r}^{2} + \sqrt{ {r}^{2} + {h}^{2} } \)
\( \sf \: 31.4 = 3.14 \times {2}^{2} + \sqrt{ {2}^{2} + {h}^{2} } \)
\( \sf \: 31.4 = 3.14 \times 4 + \sqrt{ 4 + {h}^{2} } \)
\( \sf \: 31.4 =12.56 + \sqrt{ 4 + {h}^{2} } \)
\( \sf \: 31.4 - 12 .56 = \sqrt{ 4 + {h}^{2} } \)
\( \sf \: 18.84 = \sqrt{ 4 + {h}^{2} } \)
\( \sf \: 18.84 ^{2} = 4 + {h}^{2} \)
\( \sf \: 354.9456 - 4 = {h}^{2} \)
\( \sf \: 350.9456 = {h}^{2} \)
\( \sf \: h = \sqrt{ 350.9456}\)
\( \sf \: h = 18.73\)
Now put this in the first formula to find slant height (l)
\( \tt \: l = \sqrt{ {r}^{2} + {h}^{2} } \)
\( \tt \: l = \sqrt{ {2}^{2} + {18.73}^{2} } \)
\( \tt \: l = \sqrt{ 4 + 350.8129 } \)
\( \tt \: l = \sqrt{ 354.8129 } \)
\( \tt \: l = 18.83\)
The second hand on Mr. Vidler's Alarm Clock is 6 cm long. Approximately how far does the tip travel in 5 minutes and 15 seconds? [Round your answer to the nearest tenth. Only type in the number, no units.]
Answers
Answer:
3.28 cm
Step-by-step explanation:
The calculation is given below:
we assume the following things
R denotes the radius of the circle
And, A denotes An arc
Now , the length of the arc is
L = (A ÷ 360°) × 2 × 3.14 × R
According to the question
R = 6 cm
Angle = 5 minutes and 15 seconds
The clock could complete its revolution in 60 minutes
Therefore
60 minutes = 360°
Also
1 min = 60 seconds
So
1 seconds = 1min ÷ 60seconds
Now for 15 seconds it is
= 15 seconds × (1 ÷ 60)
= (15 ÷ 60) min
= 0.25 min
And for 5 minutes and 15 seconds, it is
= 5 min + 0.25 min
= 5.25 min
Also
60 minutes = 360°
So,
1 minute = 360° ÷ 60min
Now For 5.25min
= (5.25min) × (360° ÷ 60min)
= 31.5°
Finally the length would be
L = (31.5° ÷ 360°) × 2 × 3.14 × 6cm
= 3.28 cm
Erin built a wooden box to hold hay on her farm. The box is 3 m long, 1 m wide, and 1 m high. Hay costs $14 per cubic meter.
Answers
Answer:
It will cost 42 to completely fill the box with hay.
have a good day <3
2. Find the roots of the polynomial equation (point)
2x³ + 2x2-19x+ 20 = 0
Answers
Answer:
x=-4
Step-by-step explanation:
this is if by roots, the problem is asking for the zeros of the equation

The sum 51 + (-37) is equal to what? -14 88 88 14
Answers
Answer:
14
Step-by-step explanation:
Answer:
14
Step-by-step explanation:
the answer is 14 and it's postive
Ms. Ling purchases a new car for $32,000 and finances it with a 6-year simple interest loan at an annual rate of 4.25%. What are Ms. Ling’s monthly car payments rounded to the nearest cent?
Answers
Answer: 557.78$
Step-by-step explanation:
The interest: 3,200*4.25%*6
= 8,160
so the total payment: 3,200+ 8,160
= 40,160
and the monthly car payments: 40,160 divided by 6 then divided by 12 =
557.78$
or 40,160 divided by 72=
5020/9 = 557.78$
By joy Wiliams
A grocery store sells jelly beans in the bulk section for $2.75 a pound. If Wanda buys 1.8 pounds, how much will it cost?
Answers
Answer:
$4.95
Step-by-step explanation:
If jelly beans cost $2.75 per pound then multiplying the cost per pound by the amount of jelly beans purchased will give the answer of $4.95 per 1.8 pounds of jelly beans.
Question 8 (2 points) Saved
What are the ways to determine if a relation is a function? Select EACH correct
answer.
Passes a horizontal line test.
Passes vertical line test.
No repeating x values,
No repeating y values.
Answers
Answer: passes a horizontal AND vertical line test✅; no repeating x values✅
Step-by-step explanation:
To pass a line test, the function must pass BOTH the horizontal and vertical line test. If it only passes one but not the other, is it NOT a function.
Lastly, it can be a function if it has repeating y values.
Craig Milton needs to order for his company int the catalog a 20% traidor discount is offered for a price of $481.60 what is the net price
Answers
Answer:
Net price = $385.28
Step-by-step explanation:
Trade Discount - It is the discount given by buyer to seller, as a reduction in list price, when huge (bulk) orders transactions are made.
List price = 481.60
Trade Discount = 20%
So, Trade Discount = 20 / 100 (481.60) = 96.32
Net price = List price - Trade Discount = 481.60 - 96.32 = 385.28
Carly is the principal at a middle school and wants to know the average IQ of all the female, seventh-grade students. She does not know anything about what the population distribution looks like. She took a simple random sample of 31 seventh-grade girls in her school and found the average IQ score in her sample was 105.8 and the standard deviation was 15. Assume that all conditions are met, construct the 96% Confidence interval for the average IQ score of all seventh-grade girls in the school.
Answers
Answer:
The 96% confidence interval for the average IQ score of all seventh-grade girls in the school is (105, 111.6).
Step-by-step explanation:
We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.
The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So
df = 31 - 1 = 30
96% confidence interval
Now, we have to find a value of T, which is found looking at the t table, with 30 degrees of freedom(y-axis) and a confidence level of \(1 - \frac{1 - 0.96}{2} = 0.98\). So we have T = 2.15
The margin of error is:
\(M = T\frac{s}{\sqrt{n}} = 2.15\frac{15}{\sqrt{31}} = 5.8\)
In which s is the standard deviation of the sample and n is the size of the sample.
The lower end of the interval is the sample mean subtracted by M. So it is 105.8 - 5.8 = 105.
The upper end of the interval is the sample mean added to M. So it is 105.8 + 5.8 = 111.6
The 96% confidence interval for the average IQ score of all seventh-grade girls in the school is (105, 111.6).
Solve for x in [0,360) cos2x= -0.123
Answers
Write out the equation given
\(\cos 2x=-0.123\)Solving for x as shown below
\(\begin{gathered} \cos 2x=-0.123 \\ 2x=\cos ^{-1}(-0.123) \\ 2x=-(82.93^0) \end{gathered}\)Note that cosine is always negative in the second and third quadrant
The value of 2x in the second quadrant would be
\(\begin{gathered} 2x\text{ in the second quadrant is} \\ 2x=180^0-82.93^0 \\ 2x=97.07 \\ x=\frac{97.07}{2} \\ x=48.535^0 \end{gathered}\)The value of 2x in the third quadrant would be
\(\begin{gathered} 2x\text{ in the third quadrant is} \\ 2x=180^0+82.93^0 \\ 2x=262.93 \end{gathered}\)\(\begin{gathered} 2x=262.93 \\ x=\frac{262.93}{2} \\ x=131.465^0 \end{gathered}\)Hence, the values of x are 48.535° and 131.465°
Find the distance between -10.5 and 7 on a number line
Answers
Answer:
17.5
Step-by-step explanation:
cout up to zero then to 7
help!!!!!please!!!!!!!
4x = 64 + 200
what is x
Answers
x=66
Step-by-step explanation:
4x = 200 + 64 > 4x = 264 > x= 66
Answer:
x=66
Step-by-step explanation:
Steps
4x=64+200
4x=264
x=66
. Joaquin played basketball with his friends from 1:10 to 3:35. He arrived home 20 minutes later. How many minutes passed from the time Joaquin started playing basketball until the time he arrived at home?
Answers
Answer:
165 minutes
Step-by-step explanation:
To solve for the number of minutes that Joaquin played for, we can use this expression:
(let 'a' represent how much time passed from the time Joaquin started playing basketball until the time he arrived at home)
1:10 + a = 3:35Subtracting 1:10 from each side:
1:10 - 1:10 + a = 3:35 - 1:101:10 - 1:10 cancels out to 0, while 3:35 - 1:10 is equal to 2:25.
So, the expression is now:
a = 2:25So, 2 hours and 25 minutes passed.
If we know that 1 hour is equivalent to 60 minutes, we can use this expression to solve for however many minutes are in 2 hours:
2 × 60 = 120Now we need to add on the number of minutes and the time it took him to get home:
120 + 25 + 20 = 165Therefore, 165 minutes passed from the time Joaquin started playing basketball until the time he arrived at home.
Select all possible values for x if −3x < 15.
Select one or more:
A. -11
B. -7
C. -5
D. 2
E. 9
Answers
Step-by-step explanation:
When dividing or multiplying by a negative number, remember to flip the inequality sign.
-3x < 15
x > -5 (divide -3 on both sides, flip the inequality sign)
The correct options are 2 and 9. (D and E)
Answer:
D. 2
E. 9
Step-by-step explanation:
\( - 3x < 15 \\ \\ x > \frac{15}{ - 3} \\ \\ x > - 5 \\ \\ \)
Since x > - 5,
Therefore possible values of x would be 2 and 9 out of the given ones.
what is 6 5/8 + 4 3/4 in simplest terms
Answers
Answer: To find the sum of 6 5/8 and 4 3/4, you need to express the two fractions with a common denominator. One way to do this is to express both fractions with a denominator of 8. To express 6 5/8 with a denominator of 8, you can rewrite it as 6 + 5/8, and to express 4 3/4 with a denominator of 8, you can rewrite it as 4 + 3/4. When you add these two fractions, you get:
6 + 5/8 + 4 + 3/4
= 10 + 8/8
= 10 + 1
= 11 1/8
So the sum of 6 5/8 and 4 3/4 is 11 1/8. This fraction is already in simplest form, since the numerator and denominator are relatively prime (i.e., have no common factors other than 1).
Answer:
\(\frac{91}{8}\)
Step-by-step explanation:
so your question is given in mixed number
\(6\frac{5}{8} + 4\frac{3}{4}\)
now simply multiply 6 with denominator and then add 5 to it . In denominator keep 8 as it is.Follow the same process for another term as well.
= \(\frac{6*8+5}{8}\) +\(\frac{4*4+3}{4}\)
=\(\frac{53}{8}\) + \(\frac{19}{4}\)
now take LCM
=\(\frac{53*1 +19*2}{8}\)
=\(\frac{53+38}{8}\)
=\(\frac{91}{8}\)
After this if it any cancelation can be done then do cancel in denominator and numerator but here we cannot cancel so your final answer is \(\frac{91}{8}\)
1/4z+8=12
Please answer!!!!
Answers
+
32
=
48
=16
+
3
2
=
4
8
z
+
32
−
32
=
48
−
32
+
3
2
−
3
2
=
4
8
−
3
2
In a survey at a local university, 45% of students say that they get less than the recommended eight hours of sleep per night. In a group of 2300 students, how many would you expect get eight or more hours of sleep per night?
Answers
Answer: In a survey at a local university, 37% of students say that they get less than the recommended eight hours of sleep per night. In a group of 2200 students, how many would you expect get eight or more hours of sleep per night?
Please help ASAP!
(Scroll Down for Answer!)
Did you know that Algebra.Com has hundreds of free volunteer tutors who help people with math homework? Anyone can ask a math question, and most questions get answers!
OR get immediate PAID help on:
Go!!!
Answer by macston (5194) About Me (Show Source):
You can put this solution on YOUR website!
If 37% get less than 8 hours of sleep, 100%-37%=63%
63% get 8 hours or more per night:
(0.63)(2200)=1386
ANSWER: You would expect 1386 to get 8 or more hours of sleep per night.
This is an equation! Solutions: x=1.
Graphical form: Equation 3%2Ax-x%2B2=4 was fully solved.
Text form: 3*x-x+2=4 simplifies to 0=0
Cartoon (animation) form: simplify_cartoon%28+3%2Ax-x%2B2=4+%29
For tutors: simplify_cartoon( 3*x-x+2=4 )
If you have a website, here's a link to this solution.
The graph compares the weights in pounds of 100 dogs and cats that are brought in
to a veterinarian's office. Using the medians, how much more does a typical dog weigh than a typical cat?

Answers
Answer:20
Step-by-step explanation:this is wrong
Answer:
40
Step-by-step explanation:
subtract median of dogs and median of cats
Which of the following sets of ordered pairs represents a function?
{(−3, −3), (−2, −2), (−1, −1), (0, 0), (1, 1)}
{(−3, −3), (−3, −2), (−3, −1), (−3, 0), (−4, −1)}
{(−3, −3), (−3, −1), (−1, −2), (−1, −1), (−1, 0)}
{(−3 −3), (−3, 0), (−1, −3), (0, −3), (−1, −1)}
Answers
The 1st one/Top one.
X value is different each time. Function can have the same y-value (3, 1), (2, 1) but can't have the same x-value (3, 1) (3, 3)
Which statement best summarizes the “Power of a Product” property?

Answers
Answer:
A. add the exponents
Step-by-step explanation:
Answer: raise each factor to the power.
Step-by-step explanation: I did it and got it right.