Type the correct answer in each box. Spell all words correctly. Two triangles are graphed in an x y plane. The vertices are as follows: first: A (negative 6, 2), B (negative 2, 6), and C (negative 4, 2); second: A prime (negative 6, negative 2), B (negative 2, negative 6), and C (negative 4, negative 2). A sequence of transformations maps ∆ABC onto ∆A″B″C″. The type of transformation that maps ∆ABC onto ∆A′B′C′ is a . When ∆A′B′C′ is reflected across the line x = -2 to form ∆A″B″C″, vertex of ∆A″B″C″ will have the same coordinates as B′.
Answers
The transformation that mapped ∆ABC onto ∆A′B′C′ is a reflection over the x-axis. The coordinate of B'' would be same as that of B'.
How to solve transformation problems?We are given the coordinates as;
∆ABC; A(-6, 2), B(-2, 6), C(-4, 2).
∆A′B′C; A'(-6, - 2), B (-2, -6), C (-4, -2).
A) Now, we are told that ∆ABC was transformed to
∆A′B′C. From the given coordinates, we see that only the y coordinate sign changed after the transformation. Thus, the transformation that mapped ∆ABC onto ∆A′B′C′ is a reflection over the x-axis.
B) Now, ∆A′B′C′ is reflected across the line x = -2 to form ∆A″B″C″. Since the line x = -2 is vertical and the coordinate of B' in ∆A′B′C′ has an x - coordinate of -2, then it means the coordinate of B'' would be same as that of B'
Read more about transformations at; https://brainly.com/question/4289712
#SPJ1
Related Questions
The bar chart shows the amount of rubbish found on some beaches.
a) Work out the range of the number of cans found.
b) Work out the range of the number of bottles found.

Answers
a) The range of the number of cans found is: 8
b) The range of the number of bottles found is: 5
How to calculate the range of a set of data?The range of a dataset is basically the simplest measurement of the difference between values in a data set. To find the range, we will simply subtract the lowest value from the greatest value while ignoring the others.
a) The range of the number of cans found is simply the difference between the highest number of cans found and the lowest number of cans found.
Thus:
Range of number of cans = 10 - 2
Range of number of cans = 8
b) The range of the number of bottles found is simply the difference between the highest number of bottles found and the lowest number of bottles found.
Thus:
Range of number of bottles = 6 - 1
Range of number of bottles = 5
Read more about Range of Data set at: https://brainly.com/question/24326172
#SPJ1
Six times the sum of a number and 25 is at least 30
Answers
Answer:
Step-by-step explanation:
Let the number be x then:.
According to the question:
6 * (x + 25) = 30
therefore,
x + 25 = 30 / 6
x + 25 = 5
x = 5 - 25 = -20
Government economists in a certain country have determined that the demand equation for soybeans is given by
p = f(x) = 53/(2x^2)+1 where the unit price p is expressed in dollars per bushel and x, the quantity demanded per year, is measured in billions of bushels. The economists are forecasting a harvest of 2.1 billion bushels for the year, w a possible error of 10% in their forecast. Use differentials to approximate the corresponding error in the predicted price per bushel of soybeans. (Round your answer to one decimal place.)
Answers
The approximate error in the predicted price per bushel of soybeans is approximately -0.1 dollars per bushel.
To approximate the corresponding error in the predicted price per bushel of soybeans, we can use differentials. Given that the quantity demanded per year is x = 2.1 billion bushels and there is a possible error of 10% in the forecast, we need to determine the corresponding error in the predicted price per bushel.
First, let's calculate the predicted price per bushel based on the demand equation:
p = f(x) = 53/(2x^2) + 1
Substituting x = 2.1 billion bushels into the equation:
p = 53/(2(2.1)^2) + 1
Calculating the predicted price per bushel:
p ≈ 5.6746 dollars per bushel
Next, let's calculate the differential of the demand equation:
df(x) = f'(x) dx
Where f'(x) is the derivative of f(x) with respect to x, which we can find by differentiating the demand equation:
f(x) = 53/(2x^2) + 1
Taking the derivative:
f'(x) = -53/(x^3)
Now, we can calculate the error in the predicted price per bushel by considering the possible error in the quantity demanded:
dx = 0.1x
Substituting x = 2.1 billion bushels and dx = 0.1(2.1) billion bushels:
dx ≈ 0.21 billion bushels
Finally, we can use the differential to approximate the corresponding error in the predicted price per bushel:
dp ≈ f'(x) dx
dp ≈ (-53/(x^3)) (0.21)
Substituting x = 2.1 billion bushels:
dp ≈ (-53/(2.1^3)) (0.21)
Calculating the approximate error in the predicted price per bushel:
dp ≈ -0.1038 dollars per bushel
The conclusion of this topic is that by using differentials, we can approximate the corresponding error in the predicted price per bushel of soybeans based on the forecasted harvest quantity. In this case, the demand equation for soybeans, along with the forecasted harvest of 2.1 billion bushels with a possible error of 10%, allows us to calculate the approximate error in the predicted price.
To know more about error refer here:
https://brainly.com/question/29419047?#
#SPJ11
Hosiste product of 2 and 5 shown on anumber ine?

Answers
\(the \: right \: answer \: is \: of \: option \: d \\ hope \: it \: helps \\ good \: luck \: on \: your \: assignment\)
A master baker can fill a big order in 6 hours. A student baker can fill the same order in 8 hours. They start working together, and after 2 hours, the student leaves and the master baker finishes the work alone. How long will it take him to finish the order?
Answers
Answer:
It will take the master baker 2.86 hours to finish the remaining order after 2 hours.
Step-by-step explanation:
the time taken for the master baker to fill the order = 6 hours
the time taken for the student baker to fill the order = 8 hours
let the time taken for both to finish the work together if they work at the same rate = x
\(\frac{x}{8} + \frac{x}{6} =1\\\\\frac{3x + 4x}{24} = 1\\\\7x = 24\\\\x = \frac{24}{7}\\\\x = 3.43 \ hours\)
After 2 hours, the remaining time for them to finish the work together is given by;
t(remaining) = 3.43 hours - 2 hours = 1.43 hours
Working at the same rate, 2 persons will take 1.43 hours to finish the remaining work.
One person will take hour many hours ?
2 persons working at the same rate --------> 1.43 hours
1 person working at the same rate -----> ?
= 2 x 1.43 hours
= 2.86 hours
Therefore, it will take the master baker 2.86 hours to finish the remaining order after 2 hours.
Answer:
2 hours 30 minutes
Step-by-step explanation:
A bag contains 6 red balls and 5 black balls . Two balls are picked , one after the other . Find the probability that :
i. Both are black
ii. The first is black
iii. Both are of the same colour
Given that :
a. it is without replacement
b. it is with replacement
Answers
Answer:
There are:
6 red balls - R5 black balls - BTotal number = 11 ballsA. Without replacementi. Two blacks
P(BB) = 5/11*4/10 = 2/11ii. The first is black
P(B) = 5/11or, alternatively
P(BR or BB) = 5/11*6/10 + 2/11 = 3/11 + 2/11 = 5/11iii. Both are of same colour
P(BB or RR) = 2/11 + 6/11*5/10 = 2/11 + 3/11 = 5/11B. With replacementi. Two blacks
P(BB) = 5/11*5/11 = 25/121ii. The first is black
P(B) = 5/11or alternatively
P(BR or BB) = 5/11*6/11 + 25/121 = 30/121 + 25/121 = 55/121 = 5/11iii. Both are of same colour
P(BB or RR) = 5/11*5/11 + 6/11*6/11 = 25/121 + 36/121 = 61/121pls help soon I need this asap

Answers
Answer:
QPS=110
m<2= 55
m<7=35
m<3=35
m<PQR=70
Step-by-step explanation:
the two lines interesting the rhombus were perfectly cut in half
the thomas family had an opportunity to by 50 acres of land for $800 per acre. in the past the price of land had risen 3% per year. how long will it be before the land is worth $1000 per acre? explained
Answers
Given:
Initial value = $800 per acre
Growth rate = 3% per year
To find:
How long will it be before the land is worth $1000 per acre.
Solution:
The exponential growth model is:
\(y=a(1+r)^t\)
Where, y is the new value, a is the initial value, r is the growth rate in decimal and t is the number of years.
Putting \(y=1000, a=800, r=0.03\), we get
\(1000=800(1+0.03)^t\)
\(\dfrac{1000}{800}=(1.03)^t\)
\(1.25=(1.03)^t\)
Taking log both sides, we get
\(\log 1.25=\log (1.03)^t\)
\(0.09691=t\log (1.03)\)
\(0.09691=0.012837t\)
Isolating the variable t, we get
\(\dfrac{0.09691}{0.012837}=t\)
\(7.54927=t\)
\(t\approx 7.55\)
Therefore, the land is worth $1000 per acre after 7.55 years.
Which equation represents a hyperbola with a center at (0, 0), a vertex at (−48, 0), and a focus at (50, 0)? = 1 = 1 = 1 = 1
Answers
The equation that represents a hyperbola with a center at (0, 0), a vertex at (−48, 0), and a focus at (50, 0) is (x^2 / 48^2) - (y^2 / b^2) = 1.
A hyperbola is a type of conic section with two branches that are symmetric to the x-axis and y-axis. The center of the hyperbola is given as (0, 0), which means the x-axis and y-axis intersect at the center. The vertex is given as (-48, 0), which is on the x-axis. This means that the hyperbola opens horizontally.
The standard form equation for a hyperbola with a horizontal transverse axis is (x^2 / a^2) - (y^2 / b^2) = 1, where a represents the distance from the center to the vertex, and b represents the distance from the center to the foci.
In this case, since the vertex is at (-48, 0), a = 48. The focus is given as (50, 0), which is 2 units to the right of the center. Therefore, c = 2. The relationship between a, b, and c for a hyperbola is given by the equation c^2 = a^2 + b^2.
Substituting the values into the equation, we have:
(2^2) = (48^2) + (b^2)
4 = 2304 + b^2
b^2 = -2300
Since b^2 is negative, this hyperbola does not exist. There is no equation that represents a hyperbola with the given conditions.
Know more about hyperbola here:
https://brainly.com/question/19989302
#SPJ11
a company orders 29 boxed lunches from a deli for $339.30. assume each boxed lunch is the same price. if c represents the total cost in dollars and cents of the lunch order for any number, b, of boxed lunches ordered, write a proportional equation for c in terms of b that matches the context.
Answers
Answer:
11.7b
Step-by-step explanation:
If you do 339.30 divided by 29 it equals 11.7 but the full equation would be c=11.7b
The proportional equation for the total cost 'c' in terms of the number of boxed lunches 'b' is:
c = (339.30 / 29) * b
What is proportion?
The size, number, or amount of one thing or group as compared to the size, number, or amount of another. The proportion of boys to girls in our class is three to one.
Let's assume that each boxed lunch costs the same amount, denoted by the variable 'x'.
We are given that the company ordered 29 boxed lunches for a total cost of $339.30. Therefore, we can write the equation:
29x = 339.30
To find the cost 'c' for any number 'b' of boxed lunches, we can set up a proportion:
29x / 29 = 339.30 / b
Simplifying this equation, we get:
x = 339.30 / 29
Now, we can substitute this value of 'x' back into the equation:
c = bx = b * (339.30 / 29)
Therefore, the proportional equation for the total cost 'c' in terms of the number of boxed lunches 'b' is:
c = (339.30 / 29) * b
To learn more about the proportion visit:
brainly.com/question/870035
#SPJ4
A small regional carrier accepted 20 reservations for a particular flight with 19 seats. 11 reservations went to regular customers who will arrive for the flight. Each of the remaining passengers will arrive for the flight with a 53% chance, independently of each other.
Answers
The probability that all the 9 remaining passengers who have reserved the seats will arrive for the flight is 0.0215.
A small regional carrier accepted 20 reservations for a particular flight with 19 seats. Eleven reservations went to regular customers who will arrive for the flight. Each of the remaining passengers will arrive for the flight with a 53% chance, independently of each other.In the scenario given, a small regional carrier has accepted 20 reservations for a particular flight with 19 seats.
Eleven of these reservations have been made by regular customers, who the carrier is certain will arrive for the flight. Therefore, the seats of these 11 customers are confirmed and hence will be occupied.In order to determine how many seats will be filled in total, it is necessary to calculate the probability of each of the remaining 9 passengers who reserved seats arriving for the flight.
Each of these passengers has a 53% chance of arriving, independently of each other. Therefore, the probability that all 9 remaining passengers will arrive for the flight can be determined as follows:
P(all 9 remaining passengers arrive) = 0.53^9 = 0.0215.Approximately 2.15% of the time, all of the remaining 9 passengers will arrive for the flight, which will fill all 19 seats.
The probability of this occurring is relatively low, and it's therefore possible that not all seats will be filled. There is a chance that some seats will be empty if some of the remaining passengers do not arrive on the day of the flight, which will lead to a loss of revenue for the carrier.
Hence, in conclusion, the probability that all the 9 remaining passengers who have reserved the seats will arrive for the flight is 0.0215.
Know more about probability here,
https://brainly.com/question/31828911
#SPJ11
Let theta be an acute angle of a right triangle. Find the values of the other five trigonometric functions of theta.

Answers
The exact values of the remaining trigonometric functions are listed below:
Case 3: cos θ = 3 / 5, tan θ = 4 / 3, cot θ = 3 / 4, sec θ = 5 / 3, csc θ = 5 / 4
Case 4: sin θ = √11 / 6, tan θ = √11 / 5, cot θ = 5√11 / 5, sec θ = 6 / 5, csc θ = 6√11 / 11
Case 5: cos θ = 8√73 / 73, sin θ = 3√73 / 73, tan θ = 3 / 8, cot θ = 8 / 3, csc θ = √73 / 3
Case 6: sin θ = 1 / 2, cos θ = √3 / 2, tan θ = √3 / 3, sec θ = 2√3 / 3, csc θ = 2
How to find the exact values of trigonometric functions
In this problem we find four cases of trigonometric functions, whose exact values of remaining trigonometric functions must be found. The trigonometric functions are defined below:
sin θ = y / √(x² + y²)
cos θ = x / √(x² + y²)
tan θ = y / x
cot θ = x / y
sec θ = √(x² + y²) / x
csc θ = √(x² + y²) / y
Now we proceed to determine the exact values of the trigonometric functions:
Case 3: y = 4, √(x² + y²) = 5
x = √(5² - 4²)
x = 3
cos θ = 3 / 5
tan θ = 4 / 3
cot θ = 3 / 4
sec θ = 5 / 3
csc θ = 5 / 4
Case 4: x = 5, √(x² + y²) = 6
y = √(6² - 5²)
y = √11
sin θ = √11 / 6
tan θ = √11 / 5
cot θ = 5√11 / 5
sec θ = 6 / 5
csc θ = 6√11 / 11
Case 5: x = 8, √(x² + y²) = √73
y = √(73 - 8²)
y = 3
cos θ = 8√73 / 73
sin θ = 3√73 / 73
tan θ = 3 / 8
cot θ = 8 / 3
csc θ = √73 / 3
Case 6: x = √3, y = 1
sin θ = 1 / 2
cos θ = √3 / 2
tan θ = √3 / 3
sec θ = 2√3 / 3
csc θ = 2
To learn more on trigonometric functions: https://brainly.com/question/25618616
#SPJ1
HELP I WILL GIVE YOU BRAINLIEST
Question: What is the solution to this quadratic?
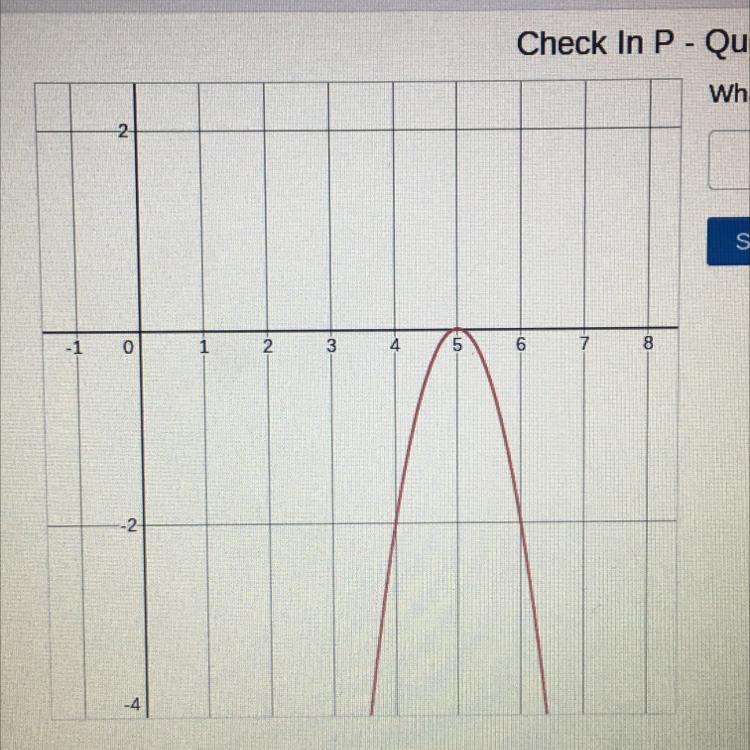
Answers
I think it is 5 because it crosses on the x axis at 5
solve 2/3x + 4 = 5/6x by eliminating the fraction.
Answers
The value of x in the given equation is 24.
Given equation:
(2/3)x + 4 = (5/6)x
We have to find the value of x by eliminating the fraction.
Fraction
Fraction is termed as a portion or section of any quantity. It is denoted by using ‘/’ symbol, such as a/b. For example, in 2/4 is a fraction where the upper part denotes the numerator and the lower part is the denominator.
LCM (3,6) = 6
Multiplying the whole equation by 6, we get:-
(2/3)x*6 + 4*6 = (5/6)x*6
4x + 24 = 5x
5x - 4x = 24
x = 24
Hence, the value of x is 24.
To learn more about Fraction, here:-
https://brainly.com/question/10354322
#SPJ1
The power rule for the logarithms states that logbMp = _____ The logarithm of a number with an exponent is the _______ of the exponent and the logarithm of that number.
Answers
The power rule for logarithms states that logb(M^p) = p * logb(M). The logarithm of a number with an exponent is the product of the exponent and the logarithm of that number.
The power rule states that logb(M^p) = p * logb(M), where M, b, and p are positive real numbers.
To understand this rule, let's consider an example. Suppose we have log2(8^2). According to the power rule, this is equivalent to 2 * log2(8).
In this case, M is 8, b is 2, and p is 2. The power rule tells us that we can bring the exponent (p) down and multiply it with the logarithm of the base (b) raised to the number (M).
So, log2(8^2) can be simplified as 2 * log2(8), which is 2 * 3 = 6.
In general, the power rule allows us to simplify logarithmic expressions by bringing the exponent down and multiplying it with the logarithm of the base.
This rule is particularly useful when dealing with complex logarithmic expressions and simplifying them to a more manageable form.
Learn more about logarithm at https://brainly.com/question/28346542
#SPJ11
The image below showcases a right triangle .
My questions:
What is a c, what does that represent
What is this problem asking for me
How do I solve this problem? Are there any formulas in place?

Answers
The perimeter of triangle is 66.24 units.
What is triangle?
In Euclidean geometry, any 3 points, once non-collinear, verify a unique triangle and at the same time, a unique plane
Main body:
according to question :
c = 28
let the vertices be A,B,C
∠A= 30°
by using trigonometric ratios,
BC/ AB = sin30°
AB = C = 28
BC/28 = sin30°
BC = 28*sin30°
BC= 28*(1/2)
BC = 14
similarly
AB /CA = cos 30°
28/CA = √3/2
CA = 28*√3/2
CA = 14/√3
CA = 24.24
Hence , perimeter = AB +BC +CA = 28+14+24.24
=66.24 units
To know more about perimeter , visit:
https://brainly.com/question/25092270
#SPJ1
1.)
Joel is 6 ft tall. He notices that the distance from the top of his head to the tip of his shadow is 16 ft. What is the measure x of the angle that his shadow makes with the hypotenuse of the right triangle? Round the angle measure to the nearest whole number degree.
(Use an inverse trig function)
2.)
Which formula (Pythagorean Theorem) can be used to find length of Joel’s shadow?
A.) 6^2 + x^2 + 16^2
B.) 6^2 + x^2 = 16^2
C.) 6^2 + 16^2 = x^2
D.) x^2 + 16^2 = 6^2

Answers
Part(1)
The measure of the angle will be 45°.
Part(2),
The formula for the shadow is,
6² + x² = 16²
A basic mathematical theorem relating to the lengths of a right-angled triangle's sides is known as the Pythagorean theorem. According to this rule, the square of the length of the hypotenuse (the side that faces the right angle) in any right-angled triangle equals the sum of the squares of the lengths of the other two sides.
Part(1),
To find the angle x, we can use the inverse tangent function. Let's call the length of Joel's shadow "s". Then we have:
tan(x) = opposite/adjacent = 16/s
Taking the inverse tangent of both sides, we get:
x = tan⁻¹(16/s)
We know that Joel's height is 6 ft, so the hypotenuse of the right triangle formed by Joel and his shadow is:
= √(6² + s²)
Now we can use the Pythagorean Theorem to solve for s. Rearranging the formula for h, we have:
s = √(h² - 6²)
Substituting the value of h with the expression above, we get:
s = √((√(6² + s²))² - 6²)
Simplifying this expression, we get a quadratic equation in terms of s:
s² - 256 = 0
Solving for s, we get:
s = ±16
Since s represents the length of the shadow, it must be positive. Therefore, s = 16 ft.
Substituting s into the equation for x, we get:
x = tan⁻¹(16/16) = tan⁻¹(1) = 45°
So the measure of the angle x is 45 degrees.
Part(2),
The formula for a shadow can be written as,
6² + x² = 16²
To know more about the Pythagorean theorem follow
https://brainly.com/question/21332040
#SPJ1
Which statements about mass are true?
Select each correct answer.
Responses
One kilogram is 100 times less than one gram.
One kilogram is 100 times less than one gram.
Grams are greater than kilograms.
Grams are greater than kilograms.
One kilogram is 100 times greater than one gram.
One kilogram is 100 times greater than one gram.
Kilograms are greater than grams.
Kilograms are greater than grams.
One kilogram is 1,000 times greater than one gram.
One kilogram is 1,000 times greater than one gram.
One kilogram is 1,000 times less than one gram
Answers
Answer:
Step-by-step explanation:
one kilogram is 100 times less than one gram
what is the value of (x - y) (x - y) if xy = 3 and x2 y2 = 25?
Answers
The value of (x - y)(x - y), if xy = 3 and x² + y² = 25, is 19.
A binomial is an expression represented by the sum or a difference of two algebraic terms. Generally, we can express it as a+b. If we square this binomial, (a + b)², it can be expanded into a² + 2ab + b².
xy = 3
x² + y² = 25
Now, (x - y)(x - y) = x² + y² -xy -xy
(x - y)(x - y) = x² + y² -2xy
Now put the values of x² + y² and xy
(x - y)(x - y) = 25 - 2 × 3
(x - y)(x - y) = 25 - 6
(x - y)(x - y) = 19
To know more about binomial, here
https://brainly.com/question/13870395
#SPJ4
Which describes the graph of the function between x = 4 and x = 8 ?
A. Thefunction is nonlinear and increasing.
B. The function is nonlinear and decreasing.
C. The function is linear and increasing.
D. The function is linear and decreasing.

Answers
Answer:
D
Step-by-step explanation:
I think its D because linear mmeans the lines connect, and from the point ut goes down making the parabola go downwards and decrease
Simplify to a single power of 4:

Answers
Answer:
\(4^8\)
Step-by-step explanation:
Formula: \((a^b)^c = a^{bc}\)
Solve:
\((4^2)^4\)\(4^{2*4}\)\(4^8\)-Chetan K
Is -10/7 equivalent to big -3 and 1/7? Why or why not, I need to show -10/7 as a mixed fraction
Answers
Answer: No
Explanation:
Since 7 goes into 10 once, we can subtract 7 from 10 and see what the remainder is.
10 - 7 = 3.
Knowing that, our mixed number ("mixed fraction") will look like this:
-1 \(\frac{3}{7}\)
We can now answer the question,
Does -1 \(\frac{3}{7}\) = -3 \(\frac{1}{7}\)?
No, -1 \(\frac{3}{7}\) ≠ -3 \(\frac{1}{7}\).
solve by using substitution and elimination method

Answers
The solutions to the system of equations in this problem are given as follows:
(-1,1) and (4,5).
How to solve the system of equations?The first equation in this system is given as follows:
\(\frac{5}{x + 1} - \frac{2}{y - 1} = \frac{1}{2}\)
Applying the least common factor, the expression is given as follows:
\(\frac{5(y - 1) - 2(x + 1)}{(x + 1)(y - 1)} = \frac{1}{2}\)
\(\frac{-2x + 5y - 7}{(x + 1)(y - 1)} = \frac{1}{2}\)
Applying cross multiplication, we have that:
-4x + 10y - 14 = (x + 1)(y - 1)
-4x + 10y - 14 = xy - x + y - 1
xy + 3x = 9y - 13.
x(y + 3) = 9y - 13
x = (9y - 13)/(y + 3).
The second equation is given as follows:
\(\frac{10}{x + 1} + \frac{2}{y - 1} = \frac{5}{2}\)
Hence:
\(\frac{10(y - 1) + 2(x + 1)}{(x + 1)(y - 1)} = \frac{5}{2}\)
\(\frac{10y + 2x - 8}{(x + 1)(y - 1)} = \frac{5}{2}\)
5(x + 1)(y - 1) = 20y + 4x - 16
5(xy - x + y - 1) = 20y + 4x - 16
5xy - 5x + 5y - 5 = 20y + 4x - 16
9x - 5xy = -15y + 11
x(9 - 5y) = -15y + 11
x = (-15y + 11)/(9 - 5y)
Equaling both equations of x, the solution for y is obtained as follows:
(9y - 13)/(y + 3) = (-15y + 11)/(9 - 5y)
Applying cross multiplication, and then combining the like terms, we have that the simplified expression is of:
y² - 6y + 5 = 0.
(y - 1)(y - 5) = 0.
When y = 1, the solution for x is given as follows:
(-15 + 11)/(9 - 5) = -4/4 = -1.
When y = 5, the solution for x is given as follows:
x = (-15(5) + 11)/(9 - 5(5)) = 4.
More can be learned about a system of equations at https://brainly.com/question/24342899
#SPJ1
Unit 8: right triangles and trigonometry
Homework 2: special right triangles
HELP PLEASE!!

Answers
Answer:
x=50
y=25
Step-by-step explanation:
So for this triangle we can use trig. To find side x (the hypotenuse) we can do sin60 degrees. *remember SOHCAHTOA, so sin is opposite over hypotenuse.
sin60degrees=(25 * sqrt of 3)/x
multiply each side by x to get xsin60degrees=25*sqrt of 3. Then divide both sides by sin60degrees. Plug that in a calculator and you should get 50.
For side y, well you can use the characteristics of 30-60-90 triangles and by doing this we know that the short leg of this type of triangle is HALF of the hypotenuse and half of 50 is 25. If you didn't know this you could still use the cos of 60 degrees and get 25 as well.
Simplify the given equation.
5x + 2(x-3) = -2(x - 1)
O 7x-3= -2x - 1
O 7x-6= -2x + 2
O 7x-6= -2x - 2

Answers
Answer:
2) 7x-6=2x+2
Step-by-step explanation:
It equals 8/9, and the equation, (5x + 2(x-3) = -2(x - 1)) equals 8/9 as well.
both fencers start attacks simultaneously. while attacking, fencer x makes a feint. fencer y makes a direct attack. both hit at the same time and land on valid target. what should the referee do
Answers
The referee should call a double touch and have the fencers restart the point.
A double touch occurs when both fencers land a valid touch on the opponent at the same time. In this case, fencer X made a feint, which is an attempt to draw the opponent into a reaction. Fencer Y responded with a direct attack. Since both fencers landed a valid touch at the same time, the referee should call a double touch.
A double touch is a situation in which both fencers hit the other at the same time, and the point is not awarded to either fencer. The referee has the power to decide if a double touch occurred, and the fencers will restart the point if a double touch is called. To ensure fairness, the referee should observe both fencers carefully and make a judgment on who initiated the attack and who responded.
If both fencers hit at the same time and the referee cannot determine who initiated the attack, then a double touch should be called.
Learn more about Fencers here:
https://brainly.com/question/28479996
#SPJ4
you are trying to estimate the percent of people in california who have a college degree. you randomly sample 60 individuals, and 18 of them say they have a college degree. using the appropriate rule of thumb, answer: is it ok to use these numbers to calculate a 99%-confidence interval for the percent of all california residents with a college degree?
Answers
Yes , it ok to use these numbers to calculate a 99%-confidence interval for the percent of all California residents with a college degree.
This will give us 99 percent confidence interval when using the formula with a sample proportion of 18 and a sample size of 60.
The fraction (frequency) of acceptable confidence intervals that contain the true value of the unknown parameter is represented by the confidence level. In other words, the confidence intervals are calculated from an infinite number of independent samples using the chosen confidence level.
As a result, the fraction of the range containing the true value of the parameter equals the confidence level.
Before evaluating the data, the confidence level is usually chosen. The 95% confidence level is the most usually utilised. However, additional confidence levels, such as 90% and 99%, are also employed.
To learn more about confidence intervals
brainly.com/question/29680703
#SPJ4
Traffic Jam
There are 8 cans of strawberry jam, 7 raspberry jam,
and 5 cherry jam in the cellar. You're trying to sneak
some out, but don't want to attract attention or take
too many. It's dark, so you can't tell what kind of jam
you're taking.
How many cans can you sneak out of the
cellar in the dark with the certainty that there
will still be at least 4 cans of one kind of jam
and 3 cans of another left over?
Answers
Answer:
Hey!
You could obviously count how many you're taking, so that's 7 left behind. My guess is that you could taste the jam... but that's the best I've got.
The requreid we can sneak out 9 cans of jam in the dark and still be sure that there will be at least 4 cans of one kind of jam and 3 cans of another left over.
What is arithmetic?It involves the basic operations of addition, subtraction, multiplication, and division, as well as more advanced operations such as exponents, roots, logarithms, and trigonometric functions.
Let's first find the minimum number of cans that need to be left in the cellar to meet the given criteria. We want at least 4 cans of one kind of jam and 3 cans of another leftover. This means we can take a maximum of:
8 - 4 = 4 cans of strawberry jam
7 - 3 = 4 cans of raspberry jam
5 - 3 = 2 cans of cherry jam
So, we can take a maximum of 4 + 4 + 2 = 10 cans in total.
To have certainty that we meet the criteria, we need to take one less than the maximum number of cans, which is 9 cans. So, we can sneak out 9 cans of jam in the dark and still be sure that there will be at least 4 cans of one kind of jam and 3 cans of another left over.
Learn more about arithmetic here:
https://brainly.com/question/11424589
#SPJ2
simplify 2^(x+2) /2^(x-1)
Answers
Answer:
Step-by-step explanation:
When we divide two exponential expressions with the same base, we can subtract their exponents. Using this property, we can simplify the given expression as:
2^(x+2) /2^(x-1) = 2^x * 2^2 / 2^x * 2^(-1)
= 2^(x-1+2)
= 2^(x+1)
Therefore, the simplified expression is 2^(x+1).
Select the correct answer. The table represents quadratic function g. Which statement is true about the function? A. The maximum occurs at the function’s y-intercept. B. The maximum occurs at the function’s x-intercept. C. The minimum occurs at the function’s y-intercept. D. The minimum occurs at the function’s x-intercept.
Answers
The maximum of the given quadratic function table occurs at the x-intercept.
How to interpret Function Tables?From the given function table, we see that;
At x = 0, y = -16
At x = 1, y = -9
At x = 2, y = -4
At x = 3, y = -1
At x = 4, y = 0
At x = 5, y = -1
Now, the maximum of the function will be the greatest value of y and from the table values we see that the greatest value of y is 0.
Thus, the maximum of the function occurs at the x-intercept.
Read more about Function tables at; https://brainly.com/question/3632175
#SPJ1
