Two sides of a triangle have the following measures. Find the range of possible measures for the third side (x).
11, 8
Answers
The range of possible measures for the third side (x) is 3 < x < 19. To find the range of possible measures for the third side of a triangle, we can use the triangle inequality theorem.
According to this theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
According to the Triangle Inequality Theorem, the total of any two sides of a triangle must be bigger than the length of the third side. To put it another way:
For a triangle with sides of a, b, and c lengths:
Any two sides' total must be bigger than the length of the third side.This may be represented mathematically as:
a + b > c b + c > a c + a > b
This theorem tells us if a given set of side lengths may be used to build a valid triangle. If any of the preceding requirements are not met, it is impossible to build a triangle with those side lengths.
In this case, the two sides of the triangle are 11 and 8. Therefore, we can set up an inequality as follows:8 + 11 > x. This can be simplified as:19 > x.
Thus, the length of the third side (x) must be less than 19. In addition, the length of the third side cannot be less than the difference between the two sides or more than their sum, which are 3 and 19, respectively.Therefore, the range of possible measures for the third side (x) is 3 < x < 19.
For more question on inequality
https://brainly.com/question/16909785
#SPJ11
Related Questions
evaluate the integral. (use c for the constant of integration.) 10 cos5(x) sin4(x) dx
Answers
The result of the integral is (10/5)sin^5(x) - (20/7)sin^7(x) + (10/9)sin^9(x) + c. To evaluate the integral ∫10cos^5(x)sin^4(x)dx, we can use a trigonometric identity and a substitution.
To simplify the integrand, we can use the trigonometric identity cos^2(x) = 1 - sin^2(x) and substitute u = sin(x).
Apply the trigonometric identity: cos^5(x) = (1 - sin^2(x))^2 * cos(x) = (1 - u^2)^2 * cos(x). Now we have the integrand as 10(1 - u^2)^2 * cos(x) * u^4.
Use the substitution: Let u = sin(x), then du = cos(x)dx. We can rewrite the integral as ∫10(1 - u^2)^2 * u^4 * du.
Expand the integrand: 10u^4 - 20u^6 + 10u^8.
Integrate each term: The integral of u^4 is u^5/5, the integral of u^6 is u^7/7, and the integral of u^8 is u^9/9.
Substitute back: Replace u with sin(x) in the antiderivative expression obtained in the previous step.
Add the constant of integration, c, to obtain the final result.
To learn more about trigonometric identity click here:
brainly.com/question/12537661
#SPJ11
the number of contaminating particles on a silicon wafer prior to a certain rinsing process was determined for each wafer in a sample of size 100, resulting in the following frequencies: number of particles 0 1 2 3 4 5 6 7 frequency 1 2 3 12 11 15 18 10 number of particles 8 9 10 11 12 13 14 frequency 12 4 5 3 1 2 1 a. what proportion of the sampled wafers had at least one particle? at least five particles? b. what proportion of the sampled wafers had between five and ten particles, inclusive? strictly between five and ten particles? c. draw a histogram using relative frequency on the vertical axis. how would you describe the shape of the histogram?
Answers
The solution is,
1. a, 99% b71%
2. 64%, 44%
3. Number of particles 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
frequencies: 1, 2, 3, 12, 11, 15, 18, 10, 12, 4, 5, 3, 1, 2, 1
Relative frequencies 0.01, 0.02,0.03,0.12,0.11,0.15, 0.18,0.1, 0.12,0.04, 0.05,0.03,0.01,0.02,0.01
What is histogram?A histogram is an approximate representation of the distribution of numerical data.
here, we have,
Number of particles: 0, 1, 2, 3, 4, , 5, 6, 7
Frequency: 1, 2, 3, 12, 11, 15, 18, 10
Number of particles: 8, 9, 10, 11, 12, 13, 14
Frequency: 12, 4, 5, 3, 1, 2, 1
we solve by saying that . one of th smaples wafer is with any particles. we get the proportion by subtracting 1 from the total divided by 100
100-1/100
.99
at least five particles , then we can subtract the number of those with particles less than five from 100 , divided by 100
100-(11+12+3+2+1)=71/100
0.71 or 71%
b. those particles within 5 and 10 inclusive
15+18+10+12+4+5=64/100
0.64
0r 64%
five and 10 exclusively will be
18+10+12+4=44/100
0.44
44%
c. Draw an histogram. first we have frequency table first
Number of particles 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
frequencies: 1, 2, 3, 12, 11, 15, 18, 10, 12, 4, 5, 3, 1, 2, 1
Relative frequencies 0.01, 0.02,0.03,0.12,0.11,0.15, 0.18,0.1, 0.12,0.04, 0.05,0.03,0.01,0.02,0.01
Relative frequencies is derived by dividing each frequencies over the total frequencies
we can say that it is unimodal or say that it is slightly positively skewed
To learn more on histogram click:
brainly.com/question/17145899
#SPJ1

no links please i cant seem to find the answer for this qn

Answers
Answer:
(a) is 15
(b) is 30
75 divide by 15 times 90 divide by 15 is 30
Answer:
Step-by-step explanation:
Highest common factor of 75 and 90 will be the largest possible length of the square.
75 = 5 * 5 * 3
90 = 3 * 3 * 2 * 5
GCF = 5 * 3 = 15
Length of the side of square = 15 cm
b) Number of squares = Area of sheet ÷ Area of square
\(= \frac{75*90}{15*15}\\\\= 5 * 6\\\\= 30\)
Total number of square = 30
earth is approximately a sphere of radius 6.37 x 10 6 m. what are (a) its circumference in kilometers, (b) its surface area in square kilometers, and (c) its volume in cubic kilometers?
Answers
(a) Circumference of Earth in kilometers: 40,075.017 km
(b) Surface area of Earth in square kilometers: 510.1 million km^2
(c) Volume of Earth in cubic kilometers: 1.08 trillion km^3
To calculate these values, we use mathematical formulas that relate to the sphere shape of the Earth.
For (a), we use the formula for the circumference of a circle, C = 2 * pi * r, where r is the radius of the Earth in meters (6.37 x 10^6 m). We then convert this result to kilometers by dividing by 1000.
For (b), we use the formula for the surface area of a sphere, A = 4 * pi * r^2, where r is the radius of the Earth. Again, we convert this result to square kilometers.
For (c), we use the formula for the volume of a sphere, V = (4/3) * pi * r^3, where r is the radius of the Earth. We then convert this result to cubic kilometers by dividing by 10^9.
Learn more about Sphere:
https://brainly.com/question/22807400
#SPJ4
8.
Find the probability that two of the customers get the silver cars and one gets a white ca
Answers
Answer: 2:1
Step-by-step explanation:
the probability that they get they get the silver cars and someone else gets the white is 2:1
suppose that mean retail price per gallon of regular grade gasoline 3.43 is with a standard deviation of and that the retail price per gallon has a bell-shaped distribution. note: please use empirical rule approximations for this problem. a. what percentage of regular grade gasoline sells for between and per gallon (to decimal)? b. what percentage of regular grade gasoline sells for between and per gallon (to decimal)? c. what percentage of regular grade gasoline sells for less than per gallon (to decimal)?
Answers
The 95% of regular grade gasoline sells for between $3.23 & $3.63 and per gallon (to decimal) and 85% of regular grade gasoline sells for between $3.23 & $3.53 and per gallon (to decimal) and 16% percentage of regular grade gasoline sells for less than $3.53 per gallon (to decimal).
Suppose that mean retail price per gallon of regular grade gasoline 3.43.
empirical rule explains that approximately 68%,95% and 99.7% of data lies between (µ ± 1*σ) ,(µ ± 2*σ) and (µ ± 3*σ) respectively.
⇒If some data {x} are normally distributed, the corresponding {z} will be normal with mean 0 and standard deviation 1 where the correspondence between the {x} and {z} is given by
z = \(\frac{x-\mu}{\sigma}\)Such z's are called z-scores.
(µ ± 1*σ)=68%
(µ ± 2*σ)=95%
(µ ± 3*σ)=99.7%
a)
P(3.23<x<3.63) =\(P[ \frac{(x1- \mu)}{\sigma} < z < \frac{(x2- \mu)}{\sigma}} ]\)
=P[( \(\frac{3.23-3.43}{0.10}\) < z < \(\frac{3.63-3.43}{0.10}\) ]
=P[-2 < z < 2 ]
=0.95
=95.0 %
b)
P(3.23<x<3.53) =\(P[ \frac{(x1- \mu)}{\sigma} < z < \frac{(x2- \mu)}{\sigma}} ]\)
=P[( \(\frac{3.23-3.43}{0.10}\) < z < (\(\frac{3.53-3.43}{0.10}\) ]
=P[-2 < z < 1 ]
=0.815
=81.5 %
c)
P(x>3.53) =\(P[ z > \frac{x-\mu}{\sigma} ]\)
=P[ z > \(\frac{3.53-3.43}{0.10}\) ]
=P[ z > 1 ]
=0.16
=16.0 %.
Therefore, 95% of regular grade gasoline sells for between $3.23 & $3.63 and per gallon (to decimal) and 85% of regular grade gasoline sells for between $3.23 & $3.53 and per gallon (to decimal) and 16% percentage of regular grade gasoline sells for less than $3.53 per gallon (to decimal).
For more such questions on normal distribution
https://brainly.com/question/14916937
#SPJ4
The figure shows a line graph and two shaded triangles that are similar:
5
3
-35 -28 -21.14-70
7 14 21 28 35
B
-3
4
Which statement about the slope of the line is true? (1 point)
1) It is 7 throughout the line.
O2) It is throughout the line.
3) The slope from point o to point A is times the slope of the line from point
A to point B.
O4) The slope from point o to point A is seven times the slope of the line from
Answers
How is anyone gonna know that lol
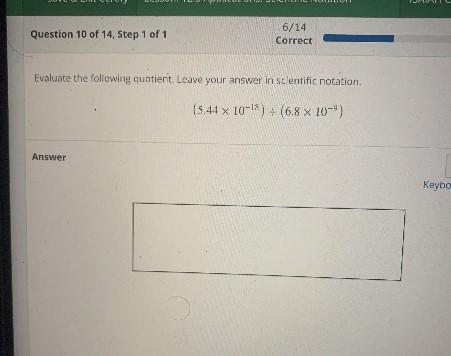
Evaluate the following quotient. Leave your answer in scientific notation(5.44 x 10-18) + (6.8 x 10-))Answer
Answers
Given:
\((5.44\times10^{-18})\div(6.8\times10^{-9})\)It can be written as follows.
\((5.44\times10^{-18})\div(6.8\times10^{-9})=\frac{5.44\times10^{-18}}{6.8\times10^{-9}}\)\(\text{Use }\frac{1}{10^{-9}}=10^9.\)\(=\frac{5.44\times10^{-18}\times10^9}{6.8^{}}\)\(=\frac{5.44\times10^{-18+9}^{}}{6.8^{}}\)\(=\frac{5.44\times10^{-9}}{6.8^{}}\)Dividing 5.44 by 6.8, we get
\(=0.8\times10^{-9}^{}\)\((5.44\times10^{-18})\div(6.8\times10^{-9})=0.8\times10^{-9}\)
Hence the quotient is
\(0.8\times10^{-9}\)given in this theorem to evaluate the integral. 2 9x dx Find the width of each subinterval in terms of n. units Find the ith endpoint in terms of n. X;= Evaluate f(x) = 9x at the ith endpoint. f(x;) = Evaluate the integral.
Answers
To evaluate the integral ∫2^9x dx, we can use the definite integral formula. Let's divide the interval [2, 9] into n subintervals of equal width.
The width of each subinterval can be found by taking the difference between the endpoints of the interval and dividing it by the number of subintervals: Δx = (9 - 2)/n. The ith endpoint, denoted as xi, can be determined by multiplying the width of each subinterval by i and adding it to the lower endpoint: xi = 2 + iΔx. We can evaluate f(xi) = 9xi at the ith endpoint by substituting xi into the function. Finally, we can evaluate the integral using the definite integral formula: ∫2^9x dx = lim(n→∞) Σ[i=1 to n] f(xi)Δx.
In summary, to evaluate the integral ∫2^9x dx, we divide the interval [2, 9] into n subintervals of equal width. The width of each subinterval is given by Δx = (9 - 2)/n. The ith endpoint, xi, is determined by multiplying the width of each subinterval by i and adding it to the lower endpoint. We evaluate f(xi) = 9xi at the ith endpoint by substituting xi into the function. Finally, we can find the integral by taking the limit of the sum of f(xi)Δx as n approaches infinity.
Now let's explain the steps in more detail. We start by finding the width of each subinterval. The interval [2, 9] has a difference of 7, and we divide it into n equal subintervals. Thus, the width of each subinterval is Δx = (9 - 2)/n.
Next, we determine the ith endpoint, xi, for each subinterval. We multiply the width of each subinterval, Δx, by i and add it to the lower endpoint of the interval. In this case, the lower endpoint is 2. Therefore, xi = 2 + iΔx.
To evaluate f(xi) = 9xi at the ith endpoint, we substitute xi into the function f(x) = 9x. This gives us f(xi) = 9(2 + iΔx).
Finally, we can evaluate the integral by taking the limit of the sum of f(xi)Δx as the number of subintervals, n, approaches infinity. The integral is expressed as ∫2^9x dx = lim(n→∞) Σ[i=1 to n] f(xi)Δx.
By following these steps and taking the limit as n approaches infinity, we can evaluate the integral.
To learn more about integral click here: brainly.com/question/31433890
#SPJ11
A ladder is placed against a building so that it reaches 35 feet up the side of the building when its base is 12 feet from the base of the building. How long is the ladder?
Answers
Answer:
35 multiplied by 12
Step-by-step explanation:
Because either you multiply it or you do sohcahtoa
5. The model below shows the ratio of gray squares to white squares. Which of the following is NOT an equivalent ratio of gray squares to white squares?

Answers
there are 5 white blocks and 4 gray blocks.
so the ratio of the gray square to white square is,
\(\frac{\text{gray}}{\text{white}}=\frac{4}{5}\)multiply numerator and denominator by 5.
\(\frac{\text{gray}}{\text{white}}=\frac{4}{5}\times\frac{5}{5}=\frac{20}{25}\)so the answer is option D
(q29) Determine c such that f(c) is the average value of the function f(x) = 4x on the interval [0, 2].
![(q29) Determine c such that f(c) is the average value of the function f(x) = 4x on the interval [0, 2].](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/cxD2rTbvoyF5jpLFcxe2I69GoxHPUrQi.png)
Answers
The value of c such that f(c) is the average value of the function f(x) = 4x on the interval [0, 2] is c = 1. Option A
How to determine c such that f(c) is the average value of the function f(x) = 4x on the interval [0, 2].The average value of a function on an interval [a, b] is given by the formula:
Average value = (1 / (b - a)) * ∫[a, b] f(x) dx
In this case, the interval is [0, 2] and the function is f(x) = 4x.
Average value = (1 / (2 - 0)) * ∫[0, 2] 4x dx
Simplifying the integral:
Average value = (1 / 2) * [\(2x^2]\) evaluated from x = 0 to x = 2
Average value =\((1 / 2) * (2(2)^2 - 2(0)^2)\)
Average value = (1 / 2) * (2 * 4 - 0)
Average value = (1 / 2) * 8
Average value = 4
Now, we want to find the value of c such that f(c) is equal to the average value, which is 4.
f(c) = 4
Substituting the function f(x) = 4x:
4x = 4
Dividing both sides by 4:
x = 1
Therefore, the value of c such that f(c) is the average value of the function f(x) = 4x on the interval [0, 2] is c = 1.
Learn more about functions at https://brainly.com/question/11624077
#SPJ1
solve equation for x -16= 3x + 11
Answers
Answer:
13.5
Step-by-step explanation:
Step 1:
x - 16 = 3x + 11 Equation
Step 2:
- 16 = 2x + 11 Subtract x on both sides
Step 3:
- 27 = 2x Subtract 11 on both sides
Step 4:
x = - 27 ÷ 2
Answer:
x = 13.5
Hope This Helps :)
Answer:
\(x = -\frac{27}{2}\)
Step-by-step explanation:
Combine like terms: x - 3x = 16 + 11Simplify: -2x = 27Divide each side by -2 to cancel out the -2 next to x. It should now look like this: x = -27/2I hope this helps!
two boats leave a port at the same time; one travels west at 20 mi/hr and the other travels south at 15 mi/hr. (a) after 30 minutes, how far is each boat from port? (b) at what rate is the distance between the boats changing 30 minutes after they leave port?
Answers
a) after 30 minutes, they will 12.5 m apart
b) 25 is the distance between the boats changing 30 minutes after they leave port
The direction of movement of both boats forms a right angle triangle. The distance travelled due south and due east by both boats represents the legs of the triangle. Their distance apart after t hours represents the hypotenuse of the right angle triangle.
Let x represent the length the shorter leg(west) of the right angle triangle.
Let y represent the length the longer leg(south) of the right angle triangle.
Let z represent the hypotenuse.
Applying Pythagoras theorem
Hypotenuse² = opposite side² + adjacent side²
Therefore
z² = x² + y²
= 20^2+15^2
z = 25
but after 30 minutes one travels 10mph
and another 7.5mph
then
z= 12.5
learn more about of speed here
https://brainly.com/question/16955861
#SPJ4
Hailey, Priya, and Shetal are auditioning for the same role. Hailey auditions at 10 minutes before four, Priya auditions 30 minutes before Hailey, and Shetal auditions at 5 minutes before four. Order the three by who will audition first. WILL GIVE BRAINLY IF CORRECT
(please answer thoughtfully with work. anyone who doesn't has there answer reported.)
Answers
Answer:
Priya, Hailey, Shetal
Step-by-step explanation:
Let's pretend the clock is currently at 4. Hailey auditioned 10 mins before, so she auditioned at 3:50.
Priya auditioned 30 mins before Hailey, meaning she auditioned at 3:20.
Then, Shetal auditioned 5 mins before 4, meaning she auditioned at 3:55.
So, going in time, the order will be 3:20, 3:50, 3:55
So, Priya, Hailey, Shetal
Is is greater than less or equal to 4.09_4.90
Answers
Its less than i think yeah
HELP ASAP PLS! THIS IS KINDA TOUGH!

Answers
Answer:
Do as a which is c if I'm not than rost me
Step-by-step explanation:
What are the domain restrictions of q^2−7q−8 divided by q^2+3q−4 ?
o q≠1 and q≠−8
o q≠−1 and q≠8
o q≠−1 and q≠4
o q≠1 and q≠−4
Answers
The domain restrictions of the expression q²−7q−8/q²+3q−4 are q ≠ -4 and q ≠ 1. (option c)
The denominator of the expression is q²+3q−4. To determine the values that would make the denominator equal to zero, we can set it equal to zero and solve for q:
q² + 3q - 4 = 0
Now, we can factorize the quadratic equation:
(q + 4)(q - 1) = 0
To find the values of q, we set each factor equal to zero and solve for q:
q + 4 = 0 or q - 1 = 0
Solving these equations, we get:
q = -4 or q = 1
So, the values of q that would make the denominator equal to zero are q = -4 and q = 1. These are the values we need to exclude from the domain of the expression to avoid division by zero.
Therefore, the correct answer is option c) q ≠ 1 and q ≠ -4.
To know more about domain here
https://brainly.com/question/28599653
#SPJ4
Complete Question:
What are the domain restrictions of q²−7q−8/q²+3q−4?
a) q≠1 and q≠−8
b) q≠−1 and q≠4
c) q≠1 and q≠−4
d) q≠−1 and q≠8
Given the function f(x)=3x^5 and g(x)=7*4^x, Which statement is true
A. f(5)>g(5)
B.f(5)
C.f(5)=g(5)
Answers
A function is defined as a relation between a set of inputs having one output each. In simple words, a function is a relationship between inputs where each input is related to exactly one output.
What is a function?The process of evaluating a function is typically straightforward when we have the function in the form of a formula. For instance, it is possible to evaluate the function f(x)=53x2 by first squaring the input number, multiplying by 3, and then subtracting the result from 5.
The algebraic expression should often take one of the following forms: addition, subtraction, multiplication, or division. Bring the variable to the left and the remaining values to the right to determine the value of x.
To determine the outcome, simplify the values. The abscissa is the x value of the point (x, y). It shows how far a point is from the origin or from the x-axis' horizontal axis.
To learn more about evaluating a function refer to:
https://brainly.com/question/2284360
#SPJ1
Please help me... due today

Answers
Answer:
The answer is B. When we count to the left the second digit is tens place
On a sunny day, Andrew, who is 1.9 m tall, casts a shadow that is 3.5 m long. A nearby tree casts a shadow that is 28.0 m long. To the nearest tenth of a metre, how tall is the tree?
Answers
Answer:
15.2
Step-by-step explanation:
The explanation is in the photo.. but basically this question is about similar triangles and you need to find the scale factor to find the height.
Hope it helps

the height of the tree is approximately 15.2 meters.
To find the height of the tree, we can set up a proportion between Andrew's height and the height of the tree based on their respective shadow lengths.
Let's denote the height of the tree as "h" meters.
The proportion between the height and shadow lengths can be written as:
h / 28.0 = 1.9 / 3.5
Now, we can solve for "h":
h = (1.9 / 3.5) * 28.0
h ≈ 15.2 meters
To the nearest tenth of a meter, the height of the tree is approximately 15.2 meters.
Learn more about proportion here
https://brainly.com/question/28005428
#SPJ2
Find the equation for the circle with a diameter whose endpoints are (2,−5​) and (-3,1).
Write the standard equation for the circle.
(Use integers or fractions for any numbers in the equation.)
Answers
The equation for the circle with a diameter whose endpoints are (2, -5) and (-3, 1) is (x - 1)^2 + (y - 1)^2 = 13.
The endpoints are (2, -5) and (-3,1).
The standard form equation for a circle is known as
\((x-a)^2+(y-b)^2=r^2\)
where (a, b) are the center's coordinates and (r) is the radius.
Taking into account the stated endpoints of the diameter. The center will then be at the midpoint, and the radius will be the distance between the center and either of the two endpoints.
Calculating the midpoint is as follows:
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
where, \((x_{1},y_{1})\) and \((x_{2},y_{2})\) are two points.
Now putting the values
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)=\left(\frac{-2+4}{2}, \frac{3-1}{2}\right)\)
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)=\left(\frac{2}{2}, \frac{2}{2}\right)\)
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)=\left(2, 1)\)
Now we determine the equation of circle.
The center (2, 1) and the terminal are the two points (-2, 3).
r = \(\sqrt{(-2-1)^2+(3-1)^2}\)
r =\(\sqrt{(-3)^2+(2)^2}\)
r = \(\sqrt{9+4}\)
r = √13
Now we can write the equation of circle as:
(x - 1)^2 + (y - 1)^2 = (√13)^2
(x - 1)^2 + (y - 1)^2 = 13
To learn more about equation for a circle link is here
brainly.com/question/29288238
#SPJ4
The complete question is:
Find the equation for the circle with a diameter whose endpoints are (2, -5) and (-3, 1).
Write the standard equation for the circle.
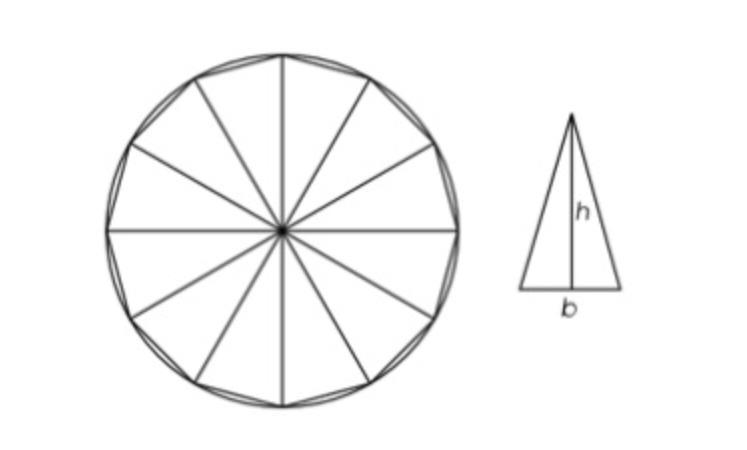
To estimate the area of the circle, Henry divides a circle of radius r into n triangles, as shown, and uses the expression (b1 + b2 + ... + bn) to estimate the area of the circle. In the expression, variables b1, b2, up to bn represent the base lengths of each triangle and h represents the height of each triangle.
Henry claims that the more triangles the circle is divide into, the closer the estimated area will be to the actual area. Which statement about Henry's claim is accurate?
Answers
Henry's claim is accurate.
What is area?Area is a quantity which explains the sai chowk to dimensional cigarette there for flannel armenia of the plane it is been thoughts as a payment of purpose that is a safe colour calculator the area of a sea for surface candy important step.
As the number of triangles increases, the estimated area will approach the actual area of the circle as the base lengths and heights of the triangles decrease. This is because the area of each triangle will approach zero, resulting in a more accurate estimate of the circle's area. Additionally, when n is large enough, the sum of the base lengths will be equal to the circumference of the circle, which is equal to the area.
To know more about area click-
https://brainly.com/question/25292087
#SPJ1
Can someone please help me

Answers
Answer:
wow
Step-by-step explanation:
Follow the steps to find the product of and 0.55.
Estimate the product of and 0.55.
1/4-
Convert the decimal 0.55 to a fraction.
V55/100
What is the product of the two numbers?
X 110/150 or 11/15
110/300 or 11/30
77/103
Answers
1) Estimate value of the product of 2/3 and 0.55 is, 2/3.
2) The fraction part is, 55 / 100
3) The product of the two numbers is, 11/30
We have to given that,
Estimate the product of 2/3 and 0.55.
And, Convert the decimal 0.55 to a fraction.
And, The product of the two numbers.
Now,
Estimate the product of 2/3 and 0.55,
So, we can round 0.55 to the nearest whole number, which is 1.
Then, multiply 2/3 by 1 to get an estimate of the product.
so, The correct answer is 2/3.
Now, we can convert the decimal 0.55 to a fraction,
= 0.55
= 55/100
= 11/20
Thus, The correct answer is, 55/100.
And, the product of 2/3 and 0.55,
= 2/3 x 55/100
= 110/300
= 11/30.
Hence, The correct answer is, 110/300 or 11/30
To know more about denominators visit-
brainly.com/question/29855437
#SPJ1
a hexadecimal number is a number written in the base 16 number system.
t
f
Answers
True. Hexadecimal numbers are written using the base 16 number system, where digits range from 0 to 9 and A to F. They are commonly used in computer systems for concise representation and easy conversion to binary.
In the hexadecimal number system, there are 16 symbols used to represent values, namely 0-9 and A-F. Each digit in a hexadecimal number represents a multiple of a power of 16.
The symbols 0-9 represent the values 0-9, respectively. The symbols A-F represent the values 10-15, respectively, where A represents 10, B represents 11, C represents 12, D represents 13, E represents 14, and F represents 15.
For example, the hexadecimal number "3F" represents the value (3 * 16^1) + (15 * 16^0) = 48 + 15 = 63 in decimal.
Similarly, the hexadecimal number "AB8" represents the value (10 * 16^2) + (11 * 16^1) + (8 * 16^0) = 2560 + 176 + 8 = 2744 in decimal.
Hexadecimal numbers are commonly used in computer systems, as they provide a convenient way to represent large binary numbers concisely. Each hexadecimal digit corresponds to a four-bit binary number, allowing for easy conversion between binary and hexadecimal representations.
for such more question on Hexadecimal numbers
https://brainly.com/question/28280312
#SPJ8
At how many points on the curve x 3 + y 3 = 9 in the xy-plane does the curve have a tangent line that is horizontal? None ) One Two Three
Answers
The answer to the question is that there are no points on the curve x3 + y3 = 9 in the xy-plane that have a tangent line that is horizontal.
The equation x3 + y3 = 9 is a cubic equation and is a non-linear equation. As such, it does not have any tangent lines that are horizontal. A tangent line is a line that just touches a point on a curve and has the same slope as the curve at that point. Since the equation is non-linear, the slope of the curve changes at each point, meaning that there cannot be any horizontal tangent lines.
To calculate the slope of the curve at any point (x,y), we use the formula m = (dy/dx) or m = 3*(x2/y2). At these points, the slope of the curve will not be zero, meaning that there is no horizontal tangent line at any point on the curve.
Therefore, the answer to the question is that there are no points on the curve x3 + y3 = 9 in the xy-plane that have a tangent line that is horizontal.
Learn more about tangent lines here:
https://brainly.com/question/23265136
#SPJ4
What is the slope of this line?
1/2
2
-2
-1/2

Answers
You can find the rise/run (slope) by finding the y-intercept on the graph (if it is on the graph which in this case it is the y-intercept is 5)
For example: if 3/4 was the slope then 3 would be the rise which means that you would move from the y-intercept upwards 3 points and 4 would be the run and would be move over to the right by 4 points. From the y-intercept you rise 3 points and run 4 points.
This graph is negative as noted by its downward direction meaning the slope will be negative.
To find the slope first find the y-intercept in this case y-intercept = 5.
Next find another solids point that also passes through the line, in this case this is point (1,3)
Move from the y-intercept (5) by -2 points or downwards by 2.
Then move over (run) by one point.
The -2 rises or in this case falls and the 1 goes to the right/runs
Insert these two numbers into the rise/run formula
-2/1 = -2
The answer is -2
Simone calculates the volume of a cube with side length 2.3 cm to be 6.9 cm3. Meiki says the volume is 12.167 cm3. Who is correct, and why?
Answers
Step-by-step explanation:
Philipp Heinrich Scheidemann was a German politician of the Social Democratic Party of Germany. In the first quarter of the 20th century he played a leading role in both his party and in the young Weimar Republic. Wikipedia
Born: July 26, 1865, Kassel, Germany
Died: November 29, 1939, Copenhagen, Denmark
Party: Social Democratic Party of Germany
Spouse: Johanna Dibbern (m. 1889–1926)
Previous offices: Mayor of Kassel (1919–1925), Chancellor of the German Reich (1919–1919), More
Books: The Making of New Germany: The Memoirs of Philipp Scheidemann
Nationality: German, Weimar
write the equation if the line in slope- intercept form that passes through (7,-4) with a slope of -1.
Answers
9514 1404 393
Answer:
y = -x +3
Step-by-step explanation:
The point-slope form can be a useful place to start.
y -k = m(x -h) . . . . . line with slope m through point (h, k)
You require the line ...
y -(-4) = -1(x -7)
y = -x +7 -4 . . . . . . . . eliminate parentheses, add -4
y = -x +3 . . . . . . . . . slope-intercept form