Turn y=1/4x+5 into standard form
Answers
Answer:
4y - x = 20
Step-by-step explanation:
Y= x/4 + 5/1
Cross multiply to get = y= (x+20/4)
4y = x+20
4y - x =20
Related Questions
Any help please? Having a hard time

Answers
Answer:
the answer is c
Step-by-step explanation:
x and y have to be at least 12, so that's why the greater than sign was used
the amount of money had to be at most $230, so that's why the less than sign was used
they said x and y represent black and white respectively, so that means x is black and y is white, so it is 18x and 20y
Answer:
x+y ≥ 12
18x+20y ≤ 230
Step-by-step explanation:
At least means that is the smallest number they can buy, so they must buy at least 12
x+y ≥ 12
no more than 230 means that is the maximum amount they can spend
18x+20y ≤ 230
Kate is a buyer for a men’s fashion retail store. She will order a new cloth overcoat from Paris for the fall fashion season. Based on her experience, she expects to sell at least 100 coats, and at most 400, but she feels that any number of sales in between is equally likely. Therefore, she estimates that her sales are uniformly distributed between 100 and 400. The total cost to the store is $100 per coat, and the retail price is set at $180. Any coats left over at the end of season would be sold at $60 each.
part 1: a) How many coats should Kate buy if she wants to maximize profits?
part 2: b) Assume Kate buys the number of coats suggested in part a), what is the probability that the coats sell out? What is the probability that they do not sell out?
Answers
Part 1: Kate should buy 100 coats to maximize profits.Part 2: The probability that the coats sell out is 0.25 (25%), and the probability that they do not sell out is 0.75 (75%).
To maximize profits, Kate should consider the scenario where she sells all the coats without any left over at the end of the season.
Since the sales are uniformly distributed between 100 and 400, buying 100 coats ensures that she meets the minimum expected sales of 100. Purchasing more than 100 coats would increase costs without a guarantee of higher sales, potentially leading to excess inventory and lower profits.
Given that the sales are uniformly distributed between 100 and 400 coats, Kate's purchase of 100 coats covers the minimum expected sales.
The probability of selling out can be calculated by finding the proportion of the range covered by the desired sales (100 out of 300). Therefore, the probability of selling out is 100/300 = 0.25 or 25%. The probability of not selling out is the complement, which is 1 - 0.25 = 0.75 or 75%.
learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
For a project in his Geometry class, Nathaniel uses a mirror on the ground to measure the height of his school’s flagpole. He walks a distance of 7.95 meters from the flagpole, then places a mirror on flat on the ground, marked with an X at the center. He then steps 1.15 meters to the other side of the mirror, until he can see the top of the flagpole clearly marked in the X. His partner measures the distance from his eyes to the ground to be 1.65 meters. How tall is the flagpole? Round your answer to the nearest hundredth of a meter.
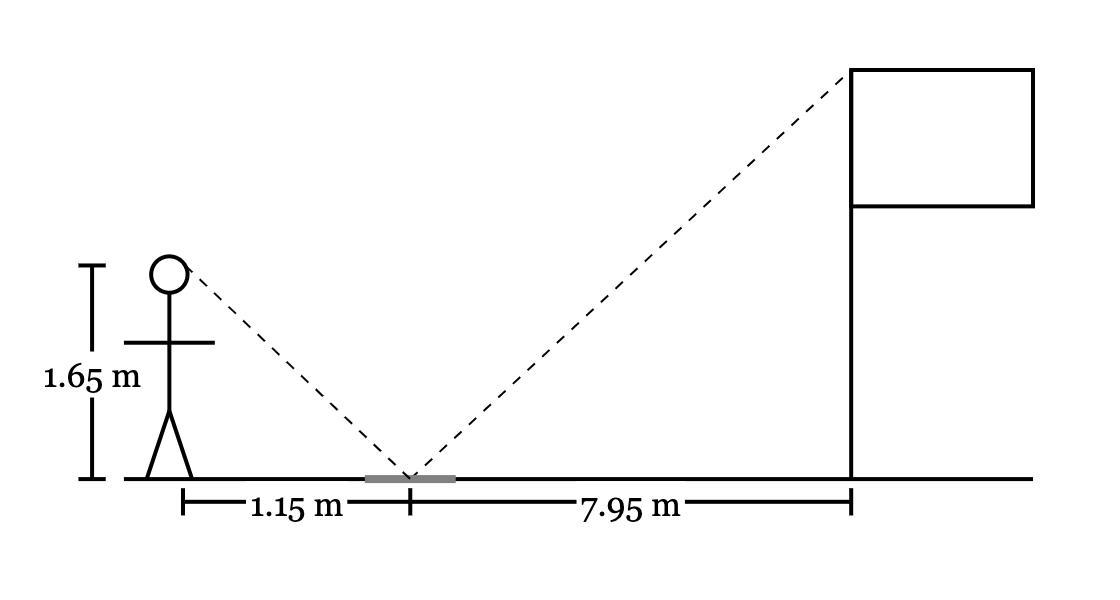
Answers
The height of the flagpole to the nearest hundredth is 11.41 m
Similar shapesIn order to get the height of the flagpole, we will use the similarity theorem of shapes.
From the given diagram, we will have the expression
1.65/1.15 = x/7.95
Cross multiply
1.15x = 1.65 * 7.95
1.15x = 13.1175
x = 13.1175/1.15
x = 11.406
Hence the height of the flagpole to the nearest hundredth is 11.41 m
Learn more on similar shapes here: https://brainly.com/question/2644832
Directions: Evaluate the following logarithmic functions.
3. log^8 64
4. log^1/3 9
5. log^1/2 1/2
6. log^49 7
7. log^9 3
8. log^3 81
9. log^4 8
10. log^100 10,000
Answers
Logarithmic functions are inverse functions of Exponential functions and are used to express very large or very small numbers. Therefore: log^100 10,000 = 2
Logarithmic functions are inverse functions of exponential functions and are used to express very large or very small numbers. The logarithm is expressed as: log x = y, where b is the base, x is the number, and y is the logarithm of x to the base b.
Example 1: log^8 644For this logarithmic function, we have: log^8 644 = X the base of the logarithm is 8, which means we can express 644 as a power of 8 raised to the value of x.8^3 = 5128^3 x 8^2 = 512 x 64 = 32768 x 8^1 = 256 x 8 = 2048
Hence, 644 can be expressed as: 644 = 8^3 + 8^2 + 8
Therefore: log^8 644 = 3 + 2 + 1 = 6
Example 2: log^1/3 9Here, we have: log^1/3 9 = x The base of the logarithm is 1/3, which means we can express 9 as a power of 1/3 raised to the value of x.1/3^-2 = 9Therefore: log^1/3 9 = -2
Example 3: log^1/2 1/2For this logarithmic function, we have: log^1/2 1/2 = x
The base of the logarithm is 1/2, which means we can express 1/2 as a power of 1/2 raised to the value of x.1/2^1 = 1/2
Therefore: log^1/2 1/2 = 1Example 4: log^49 7
For this logarithmic function, we have: log^49 7 = x
The base of the logarithm is 49, which means we can express 7 as a power of 49 raised to the value of x.49^1/2 = 7
Therefore: log^49 7 = 1/2
Example 5: log^3 81For this logarithmic function, we have: log^3 81 = x The base of the logarithm is 3, which means we can express 81 as a power of 3 raised to the value of x.3^4 = 81
Therefore: log^3 81 = 4
Example 6: log^4 8For this logarithmic function, we have: log^4 8 = x The base of the logarithm is 4, which means we can express 8 as a power of 4 raised to the value of x.4^1.5 = 8
Therefore: log^4 8 = 1.5
Example 7: log^100 10,000For this logarithmic function, we have: log^100 10,000 = x The base of the logarithm is 100, which means we can express 10,000 as a power of 100 raised to the value of x.100^2 = 10,000
Therefore: log^100 10,000 = 2
For more questions on Exponential .
https://brainly.com/question/30241796
#SPJ8
ABC and D are four towns
B is 25km due east of A
C is 25km due north of A
D is 45km due south of A
work out the bearing of B from C
Answers
Answer:
213.7°
Step-by-step explanation:
The bearing of B from D is angle ADB, which is ∠ADB = arctan(30/45)
≈ 33.7°
The bearing of D from B is that angle plus 180°, so is 180° +33.7° = 213.7°
Answer:
225°
Step-by-step explanation:
In mathematics, a bearing is defined as an angle measured clockwise from north.
See attached graph for a clearer guide to the explanations
Angle ABC is a right isosceles triangle with AB = 25 and AC = 25
m∠BAC =90°
So m∠ABC = m∠ACB = 45°
The angle at BC is 45° from the North (90°-45°) measured clockwise is 45° so we say the bearing from C to B is 045° (we use 3 digits for bearing)
The bearing from B to C on the other hand is determined by adding 180° to the bearing in the opposite direction (C to B) so the bearing from C to B is 180° +045° = 225°
(Here I am not sure whether you are supposed to answer the question in mathematical meaning of bearing or just state the direction in which BC lies relative to north. 45° clockwise from the North is in a NE direction so we can say C is NE from B but I am guessing that's not it)

2. The coordinates of Quadrilateral WXYZ are W(-1, 1), X(2, -2), Y(7, 3), and Z(4, 6). Using
coordinate geometry, prove that Quadrilateral WXYZ is a rectangle.
Answers
The proof that the Quadrilateral WXYZ is a rectangle is shown below
Proving that Quadrilateral WXYZ is a rectangle.To prove that Quadrilateral WXYZ is a rectangle, we need to show that it has four right angles.
First, we can find the slopes of each pair of opposite sides to determine if they are perpendicular.
The slope of WX is:
m(WX) = (y2 - y1)/(x2 - x1) = (-2 - 1)/(2 - (-1)) = -1
The slope of YZ is:
m(YZ) = (y2 - y1)/(x2 - x1) = (6 - 3)/(4 - 7) = -1
Since the slopes of WX and YZ are equal , we know that they are opposite sides.
Now we can use the distance formula to check if the sides of the quadrilateral are congruent. The length of WX is:
√((2 - (-1))^2 + (-2 - 1)^2) = √18
The length of YZ is:
√((7 - 4)^2 + (3 - 6)^2) = √18
The length of WY is:
√((7 - (-1))^2 + (3 - 1)^2) = √68
The length of XZ is:
√((4 - 2)^2 + (6 - (-2))^2) = √68
We can see that opposite sides WX and YZ have the same length, as do opposite sides WY and XZ.
So, the quadrilateral is a rectangle
Read more about quadrilateral at
https://brainly.com/question/23935806
#SPJ1
Assume f [a, b] → R is integrable. .
(a) Show that if g satisfies g(x) = f(x) for all but a finite number of points in [a, b], then g is integrable as well.
IF YOU ALREADY ANSWERED THIS PLEASE DO NOT RESPOND!!!
NO SLOPPY WORK PLEASE. WILL DOWNVOTE IF SLOPPY AND HARD TO FOLLOW.
PLEASE WRITE LEGIBLY (Too many responses are sloppy) AND PLEASE EXPLAIN WHAT IS GOING ON SO I CAN LEARN. Thank you:)
Answers
If g(x) = f(x) for all but finitely many points in [a, b], and f is integrable on [a, b], then g is also integrable on [a, b]. This can be proven by showing that g is bounded on [a, b] and the set of points where g and f differ has measure zero.
To show that if g satisfies g(x) = f(x) for all but a finite number of points in [a, b], then g is integrable as well, we need to prove two things:
g is bounded on [a, b].
The set of points where g and f differ has measure zero.
Proof:
To show that g is bounded on [a, b], we can use the fact that f is integrable on [a, b]. By the definition of integrability, we know that f is bounded on [a, b], i.e., there exists a constant M such that |f(x)| ≤ M for all x in [a, b]. Since g(x) = f(x) for all but a finite number of points, there are only finitely many exceptions where g and f may differ. Let's denote this set of exceptions as E.
Now, since E is finite, we can choose a constant K such that |g(x)| ≤ K for all x in [a, b] excluding the points in E. Additionally, we know that |f(x)| ≤ M for all x in [a, b]. Therefore, for any x in [a, b], we have |g(x)| ≤ max{K, M}, which means g is bounded on [a, b].
To show that the set of points where g and f differ has measure zero, we can use the fact that f is integrable on [a, b]. By the definition of integrability, we know that the set of points where f is discontinuous or has a jump discontinuity has measure zero.
Since g(x) = f(x) for all but finitely many points, the set of points where g and f differ is a subset of the points where f has a jump discontinuity or is discontinuous. As a subset of a set with measure zero, the set of points where g and f differ also has measure zero.
Therefore, we have shown that g is bounded on [a, b], and the set of points where g and f differ has measure zero. By the Riemann integrability criterion, g is integrable on [a, b].
To learn more about integration visit : https://brainly.com/question/22008756
#SPJ11
please help, I'm stuck

Answers
Answer:
Step-by-step explanation:
4
Betty has 42 butterfly stickers, as shown below.
She puts an equal number of stickers on each of 6 pages in her sticker book.
How many stickers does Betty put on each page in her sticker book?
Answers
Answer:
7
Step-by-step explanation:
42/6=7
A linear function is shown below. What point is on the graph of the inverse of this function?
a. (1, -1)
b. (-3, 5)
c. (-4, 0)
d. (7, 1)

Answers
Answer:
c. (-4, 0)
Step-by-step explanation:
F(X) = -3X - 4
Y = -3X-4
SWAP X AND Y: x = -3y -4
y = -1/3x - 4/3
f⁻¹(x) = -1/3x - 4/3
point (-4,0): x = -4 y = f⁻¹(-4) = (-1/3)*(-4) - 4/3 = 4/3 - 4/3 = 0
You are going to roll two number cubes, a white number cube and a red number cube, and find the sum of the two numbers that come up. What is the probability that the sum will be 7
Answers
The probability of obtaining a sum of 7 when rolling two number cubes is 1/6 or approximately 0.1667.
To find the probability, we need to determine the number of favorable outcomes (sum of 7) and the total number of possible outcomes when rolling two number cubes. Each cube has six faces, numbered from 1 to 6.
To obtain a sum of 7, we can have the following combinations: (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), and (6, 1). There are six favorable outcomes.
The total number of possible outcomes when rolling two number cubes is the product of the number of outcomes for each cube, which is 6 * 6 = 36.
Therefore, the probability of obtaining a sum of 7 is given by:
Number of favorable outcomes / Total number of possible outcomes = 6 / 36 = 1/6 ≈ 0.1667.
Thus, the probability that the sum of the two numbers rolled on the number cubes will be 7 is approximately 0.1667, or 1/6 when expressed as a fraction.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
a sphere is inscribed in a unit cube. a smaller cube is then inscribed within the sphere. what is the side length of the smaller cube?
Answers
Answer:10
Step-by-step explanation:
beausepppppp
The side length of the smaller cube inscribed within the sphere is approximately 0.7071.
To find the side length of the smaller cube inscribed within the sphere, which is inscribed in a unit cube, we can follow these steps:
Determine the diameter of the inscribed sphere.
Since the sphere is inscribed in the unit cube, its diameter will be equal to the side length of the unit cube. Therefore, the diameter of the inscribed sphere is 1.
Calculate the radius of the inscribed sphere.
The radius of the sphere is half of its diameter, so the radius is 0.5.
Apply the Pythagorean theorem to the smaller cube.
We can imagine a right triangle formed by half the side length of the smaller cube (let's call this length 's') and the sphere's radius (0.5) as the two shorter sides, and the diagonal of the smaller cube as the hypotenuse.
By applying the Pythagorean theorem, we get:
(s/2)^2 + (s/2)^2 = (0.5)^2
Solve for the side length 's' of the smaller cube.
Expanding the equation, we get:
2 * (s^2 / 4) = 0.25
(s^2 / 2) = 0.25
s^2 = 0.5
s = sqrt(0.5)
Express the side length 's' of the smaller cube.
The side length of the smaller cube, 's', is equal to the square root of 0.5, which can also be written as sqrt(0.5) or approximately 0.7071.
So, the side length of the smaller cube inscribed within the sphere is approximately 0.7071.
for more questions on cube
https://brainly.com/question/10421656
#SPJ11
Graph a line with a y-intercept of 3 and containing the point (2, 5).
To graph a line, plot two points on the line.
Answers
Answer:
click on the thanks



need help putting these least to greatest , 0.81 , 0.9, 0.73, 0.7
Answers
Answer:
0.7 0.73 0.81 0.9
Step-by-step explanation:
hope this helps
What is the measure WXZ equal to

Answers
Answer:
m \(\angle\) WXZ = 64°Step-by-step explanation:
From the question the two angles that's
\(\angle\) ZXY and \(\angle\) WXZ are complementary since they lie on a right angle
Complementary angles are angles that add up to 90°
Let m \(\angle\) WXZ be x
To find m \(\angle\) WXZ add up the two angles and equate them to 180° to find the angle
So we have
\(\angle\) WXZ + \(\angle\) ZXY = 90
x + 26 = 90
x = 90 - 26
x = 64°
So we have the final answer as
m \(\angle\) WXZ = 64°Hope this helps you
ignoring leap years, there are 365 days in a year. a. if people are born with equal probability on each of the 365 days, what is the probability that three randomly chosen people have different birthdates? b. if people are born with equal probability on each of the 365 days, what is the probability that 10 randomly chosen people all have different birthdates? c. if, as in fact turns out to be the case, birth rates are higher during some parts of the year than other times, would this increase or decrease the probability that 10 randomly chosen people have different birthdates, compared with your answer in part (b)
Answers
a. The probability that three people have different birthdates is 0.9918.
b. The probability that ten people have different birthdates is 0.883
c. The effect of birth rate on the probability of 10 randomly chosen people having different birthdates depends on the specifics of the distribution of birthdates.
a. To find the probability that three randomly chosen people have different birthdates, we can use the principle of inclusion-exclusion.
The probability that the first person has a unique birthdate is 1.
The probability that the second person has a birthdate different from the first is 364/365, and the probability that the third person has a birthdate different from the first two is 363/365.
Therefore, the probability that three people have different birthdates is:
1 x 364/365 x 363/365 = 0.9918
b. To find the probability that 10 randomly chosen people all have different birthdates, we can similarly use the principle of inclusion-exclusion.
The probability that the first person has a unique birthdate is 1.
The probability that the second person has a birthdate different from the first is 364/365, and the probability that the third person has a birthdate different from the first two is 363/365.
Continuing in this way, the probability that the tenth person has a birthdate different from the first nine is 356/365.
Therefore, the probability that ten people have different birthdates is:
1 x 364/365 x 363/365 x ... x 356/365 = 0.883
c. If birth rates are higher during some parts of the year than others, then it is possible that there will be more people with the same birthdate, which would decrease the probability that 10 randomly chosen people have different birthdates.
However, the effect of this depends on the distribution of birthdates.
For example, if there are more people born in the summer months, then it may be more likely that the 10 randomly chosen people have different birthdates, since they are less likely to share a birthdate in common.
On the other hand, if there are more people born in a specific month, then it may be more likely that the 10 randomly chosen people share a birthdate in common.
Ultimately, the effect of birth rate on the probability of 10 randomly chosen people having different birthdates depends on the specifics of the distribution of birthdates.
For similar question on probability.
https://brainly.com/question/911145
#SPJ11
What number are included in the et of integer? And what number are not included in the et of integer
Answers
The set of integers is the set of all whole numbers and their negative counterparts. This includes the numbers ..., -3, -2, -1, 0, 1, 2, 3, ...
Numbers that are not included in the set of integers are fractions, decimals, and other numbers that are not whole numbers. For example, the numbers 0.5, 1.6, and -3.14 are not included in the set of integers.
For example, the set of integers includes the numbers -3, -2, -1, 0, 1, 2, 3, and so on. These numbers can be negative, positive, or zero, but they must be whole numbers (that is, they must not include any fractional or decimal parts).
Numbers that are not included in the set of integers are any numbers that are not whole numbers. These include fractions, decimals, and other numbers that are not integers. For example, the numbers 0.5, 1.6, and -3.14 are not integers, because they include fractional or decimal parts.
In summary, the set of integers includes all whole numbers and their negative counterparts and excludes any numbers that are not whole numbers.
Learn more about Integers here:
https://brainly.com/question/929808
#SPJ4
1) Perform the following operations in System F(10, 5, −4, 4),
taking x = 113/8, y = 220/9 and z = −314/17. At the end, calculate
the relative error due to system restrictions and inform how many
Answers
(a) 0.0577 (b)-260.2774 (c)-7826.409 (d) 150.8776 (e) 14719.7032
(3 significant figures) .The relative error due to system restrictions for all calculations ranges from 0.0001 to 0.0132.
To perform the operations in System F(10, 5, -4, 4), we need to round the numbers to the given precision. Let's round the values of x, y, and z accordingly:
x = 113/8 ≈ 14.125
y = 220/9 ≈ 24.444
z = -314/17 ≈ -18.471
Now let's calculate the operations:
(a) 1/x + 1/y + 1/z
1/x ≈ 1/14.125 ≈ 0.0709
1/y ≈ 1/24.444 ≈ 0.0409
1/z ≈ 1/-18.471 ≈ -0.0541
1/x + 1/y + 1/z ≈ 0.0709 + 0.0409 - 0.0541 ≈ 0.0577
To determine the relative error due to system restrictions, we can compare the actual values of x, y, and z with the rounded values:
Relative error for x = |x - 14.125| / |x| ≈ |113/8 - 14.125| / |113/8| ≈ 0.0004
Relative error for y = |y - 24.444| / |y| ≈ |220/9 - 24.444| / |220/9| ≈ 0.0132
Relative error for z = |z - (-18.471)| / |z| ≈ |-314/17 - (-18.471)| / |-314/17| ≈ 0.0061
The relative error due to system restrictions is the maximum of these three values: 0.0132. To determine the number of significant figures, we look at the number with the fewest decimal places among x, y, and z. In this case, it is z with 3 decimal places. Therefore, the calculated number will have 3 significant figures.
(b) x/y + z * x
x/y ≈ 14.125 / 24.444 ≈ 0.5776
z * x ≈ -18.471 * 14.125 ≈ -260.855
x/y + z * x ≈ 0.5776 + (-260.855) ≈ -260.2774
Relative error for x/y: |0.5776 - (113/8) / (220/9)| / |0.5776| ≈ 0.0001
Relative error for z * x: |-260.855 - (-18.471 * 113/8)| / |-260.855| ≈ 0.0004
The relative error due to system restrictions is the maximum of these two values: 0.0004.
The number of significant figures is determined by the number with the fewest significant figures among x, y, and z, which is 3 significant figures.
(c) x * y * z
x * y * z ≈ 14.125 * 24.444 * (-18.471) ≈ -7826.409
The relative error for x * y * z is calculated as |(-7826.409) - (113/8) * (220/9) * (-314/17)| / |-7826.409| ≈ 0.0001.
The number of significant figures is determined by the number with the fewest significant figures among x, y, and z, which is 3 significant figures.
(d) x² - 2y
x² ≈ 14.125
² ≈ 199.7656
2y ≈ 2 * 24.444 ≈ 48.888
x² - 2y ≈ 199.7656 - 48.888 ≈ 150.8776
Relative error for x²: |199.7656 - (113/8)²| / |199.7656| ≈ 0.0001
Relative error for 2y: |48.888 - 2 * (220/9)| / |48.888| ≈ 0.0001
The relative error due to system restrictions is the maximum of these two values: 0.0001.
The number of significant figures is determined by the number with the fewest significant figures among x, y, and z, which is 3 significant figures.
(e) y³ + x/y
y³ ≈ 24.444³ ≈ 14719.1256
x/y ≈ 14.125 / 24.444 ≈ 0.5776
y³ + x/y ≈ 14719.1256 + 0.5776 ≈ 14719.7032
Relative error for y³: |14719.1256 - (220/9)³| / |14719.1256| ≈ 0.0002
Relative error for x/y: |0.5776 - (113/8) / (220/9)| / |0.5776| ≈ 0.0001
The relative error due to system restrictions is the maximum of these two values: 0.0002.
The number of significant figures is determined by the number with the fewest significant figures among x, y, and z, which is 3 significant figure.
The relative error due to system restrictions for all calculations ranges from 0.0001 to 0.0132.
Learn more about significant figures here: https://brainly.com/question/29153641
#SPJ11
The complete question is:
1) Perform the following operations in System F(10, 5, −4, 4), taking
x = 113/8, y = 220/9 and z = −314/17.
At the end, calculate the relative error due to system restrictions and inform how many significant figures the calculated number has.
(a) 1/x + 1/y + 1/z
(b) x/y + z ∗ x
(c) x ∗ y ∗ z (
d) x² − 2y
(e) y³ + x/y
Organisms A and B start out with the same
population size.
Organism A's population doubles every day. After 8
days, the population stops growing and a virus
cuts it in half every day for 2 days.
Organism B's population grows at the same rate
but is not infected with the virus. After 10 days, how
much larger is organism B's population than
organism A's population?
The expression showing organism A's increase in
population for the first 8 days is
28
The expression showing organism A's decrease in
population over the next 2 days is (1/2)2. This can be
written as (2-1)2, which is equivalent to
2-²
After 10 days, the total change in organism A's population
(combining the increase and reduction) is
Select...
which simplifies to
Select...
4 of 5 QUESTIONS
The expression showing organism B's increase in
population over the same 10 days is
Select...
The expression for how many times greater organism B's
population is than organism A's population is
Select...
After 10 days, organism B's population is
Select...
times greater than organism A's population.
Answers
The expression showing organism B's increase in population over the same 10 days is 2^10.
The expression for how many times greater organism B's population is than organism A's population is 2^2.
After 10 days, organism B's population is 4 times greater than organism A's population.
Let's calculate the population changes for organisms A and B step by step:
For Organism A:
The population doubles every day for 8 days: 2^8 = 256.
After 8 days, the population is 256.
Then, a virus cuts the population in half for 2 days: 256 * (1/2)^2 = 256 * (1/4) = 64.
After 10 days, the population of organism A is 64.
For Organism B:
The population grows at the same rate as organism A, but there is no virus.
The population doubles every day for 10 days: 2^10 = 1024.
To find how much larger organism B's population is than organism A's population after 10 days, we subtract the population of organism A from the population of organism B:Organism B's population - Organism A's population = 1024 - 64 = 960.
Therefore, after 10 days, organism B's population is 960 individuals larger than organism A's population.
The expression showing organism A's increase in population for the first 8 days is 2^8 = 256.
The expression showing organism A's decrease in population over the next 2 days is (1/2)^2 = (2^(-1))^2 = 2^(-2).
After 10 days, the total change in organism A's population is 256 * 2^(-2) = 64.
The expression showing organism B's increase in population over the same 10 days is 2^10 = 1024.
The expression for how many times greater organism B's population is than organism A's population is 1024/64 = 16.
After 10 days, organism B's population is 16 times greater than organism A's population.
for such more question on population
https://brainly.com/question/13769205
#SPJ8
without graphing, describe the end behavior of the graph of the function. f(x)=1-2x^2-x^3
Answers
The function is f(x)=1-2x^2-x^3$. End behavior is a way to talk about what happens to the graph as x approaches positive or negative infinity. End behavior is a term that describes the way a graph approaches infinity as x moves to the left or right.
Since a polynomial function can increase without limit as x approaches infinity, decrease without limit as x approaches negative infinity, or do both of these things, it is important to determine what a polynomial function does at either end of the graph. We can determine this from the degree of the polynomial and the sign of the leading coefficient.
The degree of the polynomial function $f(x)=1-2x^2-x^3$ is 3 because the highest power of x in the expression is 3. The coefficient of the term with the greatest exponent (i.e. -1) is negative in this case. The end behavior of the graph is therefore that the graph drops as x increases and also as x decreases without limit, approaching negative infinity.
Know more about end behavior:
https://brainly.com/question/25593826
#SPJ11
The average of six numbers is -3.65.If five numbers are each -3.20,what is the sixth number.
Answers
we know that the average for six numbers can be writen like:
\(A=\frac{x_1+x_2+x_3+x_4+x_5+x_6}{6}\)So if 5 of them are -3.20 and the average is -3.65 we can replace that values and find the missing one:
\(-3.65=\frac{5(-3.20)+x}{6}\)and we solve for x so:
\(\begin{gathered} -3.65\cdot6=-16+x \\ -22+16=x \\ -6=x \end{gathered}\)So the missing value is -6
0.1m+8-12n when m =30 and n =[1fraction[/4]
Answers
Answer:
Step-by-step explanation:
Root:
n≈0.00833333 m + 0.666667
Root for the variable n:
n≈-0.0833333 (-0.1 m - 8)
Derivative:
d/dm(0.1 m + 8 - 12 n) = 0.1
Indefinite integral:
integral(8 + 0.1 m - 12 n) dm = 0.05 m^2 - 12 m n + 8 m + constant
Definite integral over a disk of radius R:
integral integral_(m^2 + n^2<R^2)(0.1 m - 12 n + 8) dm dn = 8 π R^2 + 0
Definite integral over a square of edge length 2 L:
integral_(-L)^L integral_(-L)^L (8 + 0.1 m - 12 n) dn dm = 32 L^2 + 0
Consider the numbers 1 through 24 inclusive, Event A= Prime number and B = Odd number.
what is the P(A|B)?
Answers
Answer:
P(A|B) = 8/12 = 66.67%
Step-by-step explanation:
From 1 to 24, the number of odd numbers is 12, so event B has 12 possible values.
Among these 12 odd numbers in B, the ones that are prime are:
3, 5, 7, 11, 13, 17, 19, 23 (total of 8 numbers)
so given event B, the event A has 8 possible values inside the sample space of B.
So the probability of A given B, that is, P(A|B), is:
P(A|B) = 8/12 = 66.67%
I need anyone to plz answer this very soon

Answers
Answer:
29°
Step-by-step explanation:
\(In\: \triangle CDE\\\\
m\angle C + m\angle D + m\angle E = 180\degree \\\\
48\degree + 74\degree + m\angle E = 180\degree \\\\
122\degree + m\angle E = 180\degree \\\\
m\angle E = 180\degree- 122\degree \\\\
\huge \red {m\angle E = 58\degree} \\\\
\because \triangle ABC \cong \triangle DEC... (given) \\\\
\therefore \angle B \cong \angle E.. (CACT) \\\\
\therefore m\angle B = m\angle E\\\\
\therefore 2x = 58\degree \\\\
\therefore x =\frac{58\degree}{2}\\\\
\huge \orange {\boxed {\therefore x = 29\degree}}
\)
A bag of trail mix weighs 1.625 pounds. Round 1.625 to the nearest tenth.

Answers
Answer:
1.6
i think
Step-by-step explanation:
Answer:
1.6
Step-by-step explanation:
1.6
1.625
2 is closer to 0 than 10
Someone answer this plsss

Answers
The equation of the line perpendicular to the given line and that passes through the point is x + 3y = 6
From the question, we are to determine the equation of the line that is perpendicular to the given equation.
A line perpendicular to another has a slope that is the negative reciprocal of the slope of the other line.
That is,
If m₁ is the slope of one of the lines
and m₂ is the slope of the other line
Then,
m₁ = -1/m₂
First, we will determine the slope of the given line
The equation of the given line is
y = 3x - 9
Compare the equation to the general form of the equation of a straight line
y = mx + b
Where m is the slope
and b is the y-intercept
By comparison,
m = 3
∴ The slope of the given line is 3
Thus,
The slope of the line that is perpendicular to this line is -1/3
Now,
To determine the equation this line,
We have that the line passes through the point (3, 1)
Using the point-slope form of the equation of a straight line,
y - y₁ = m(x - x₁)
m = -1/3
x₁ = 3
y₁ = 1
Putting the parameters into the equation,
y - 1 = -1/3(x - 3)
Expressing the equation in standard form
3(y -1) = -1(x - 3)
3y - 3 = -x + 3
3y + x = 3 + 3
x + 3y = 6
Hence, the equation of the line perpendicular to the given line and that passes through the point is x + 3y = 6
Learn more on Equation of a line here: https://brainly.com/question/11752607
#SPJ1
Find the sum of -6x^{2}+3−6x
2
+3 and 4x^{2}-2x4x
2
−2x.
Answers
The sum of the expressions -6x² + 3 and 4x² - 2 is -2x² - 2x + 3.
What is an algebraic expression?An algebraic expression is consists of variables, numbers with various mathematical operations,
The given expressions are,
-6x² + 3 (1)
And 4x² - 2x (2)
To find sum of expressions,
Add expression (1) and (2),
= -6x² + 3 + 4x² - 2x
= -2x² - 2x + 3.
The required sum of the expressions is -2x² - 2x + 3.
To know more about Algebraic expression on:
https://brainly.com/question/19245500
#SPJ1
(a) Graph a linear function of your choice. On the same graph, graph a linear function transformed 2 units up and 3 units down.
(b) What was the equation of your linear function in slope-intercept form?
(c) What was the equation of the transformed function in slope-intercept form?
Answers
(a) The graph of the linear functions is as attached.
(b) The equation of the linear function in slope-intercept form is; y = x
(c) The equation of the transformed function in slope-intercept form is;
y = x + 2 and y = x - 3
How to interpret the graph of a Linear Function?
Functions are defined as the relationship between sets of values. For example, in the function; y = f(x), for every value of x there exists a set of y values.
x is the independent variable.
y is the dependent variable.
If the linear function is; y = x,
The equation of the transformation in slope-intercept form is given as;
For translation of 2 units up, we have;
y = x + 2
For a translation of 3 units down, we have;
y = x - 3
Thus, the required graph has been attached and the solution is determined.
Read more about Linear Function at; https://brainly.com/question/4025726
#SPJ1

simplify x+4/2 - x-5/7

Answers
Answer:
38
Step-by-step explanation:
You want to remove the denominatior so multiply both fractions by a common multiple of the denominator
14(x+4/2) - 14(x-5/7)
Simplify
14x+28 - 14x+10
Combine common variables
14x-14x+28+10
38
Done!
When the lid is left off an ink bottle, the ink evaporates at a rate of
2.5 x 10 cm³/s. A full bottle contains 36 cm³ of ink. How long, to
the nearest day, will it take for all the ink to evaporate?
Answers
Answer:
over 4 hours
Step-by-step explanation:
To find out how long it will take for all the ink to evaporate, we need to divide the total volume of ink by the rate at which it evaporates. We can do this using the following equation:
time = volume / rate
Substituting in the values from the problem, we get:
time = 36 cm³ / 2.5 x 10 cm³/s
Solving this equation, we find that it will take approximately 1.44 x 101 seconds for all the ink to evaporate. To find out how long this is in days, we need to divide by the number of seconds per day:
time = 1.44 x 101 seconds / (60 seconds/minute * 60 minutes/hour * 24 hours/day)
This works out to be approximately 0.17 days, or just over 4 hours. Therefore, it will take approximately 4 hours for all the ink to evaporate if the lid is left off the bottle.