Tina was asked to determine the possible dimensions of a given rectangle whose area is 12a4b3-18a6b3-72a7b3. Tina stated that the possible dimensions (written as a product) of the given rectangle were: 3a4b3(4-6a2-24a3). Do you agree or disagree with Tina? Explain your answer.
Answers
Answer:
Tina is correct
Step-by-step explanation:
Given
\(Area = 12a^4b^3 - 18a^6b^3 - 72a^7b^3\)
Required
State if \(3a^4b^3(4-6a^2-24a^3)\) is a possible dimension
To do this, we simply expand \(3a^4b^3(4-6a^2-24a^3)\)
\(3a^4b^3(4-6a^2-24a^3)\)
\(3a^4b^3 * 4-3a^4b^3 * 6a^2-3a^4b^3 * 24a^3\)
\(12a^4b^3 - 18a^{4+2}b^3 * -72a^{4+3}b^3\)
\(12a^4b^3 - 18a^{6}b^3 * -72a^{7}b^3\)
By comparison, the result of the expansion
\(12a^4b^3 - 18a^{6}b^3 * -72a^{7}b^3\)
and the given expression
\(Area = 12a^4b^3 - 18a^6b^3 - 72a^7b^3\)
are the same.
Hence, Tina is correct
Related Questions
Please help
Worth 20 points

Answers
Answer:
The answer is a since it is the only one which has lines going through all the points
Hope This Helps!!!
Gianna is paid $90 for 5 hours of work.
a. At this rate, how much would Gianna make for 8 hours of work?
b. At this rate, how long would Gianna have to work to make $600?
Use a ratio table to solve.
Answers
Answer:
a. $144
b. about 34 hours
Step-by-step explanation:
If Gianna is paid $90 dollars for 5 hours of work, that means that she is paid $18 an hour. So, 18x33 is 594, which means that 18x34 is $612.
Which graph shows all natural numbers less than three?

Answers
Answer:
A i think
Step-by-step explanation:
Answer:
Try b out
Step-by-step explanation:
if that isn’t working for you {because it didn’t work for me}try b because it says less the 3 b is the only one the is less then three
A population has a mean of 53 and a standard deviation of 21. A sample of 49 observations will be taken. The probability that the sample mean will be greater than 57.95 is ___. a. 0.450 b. 0.9505 c. 0.0495 d. 0
Answers
The probability that the sample mean will be greater than 57.95 is 0.0495.
What is probability?Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. This is the basic probability theory, which is also used in the probability distribution.
To solve this question, we need to know the concepts of the normal probability distribution and of the central limit theorem.
Normal probability distributionProblems of normally distributed samples can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z=\dfrac{X-\mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit TheoremThe Central Limit Theorem establishes that, for a random variable X, with mean \(\mu\) and standard deviation \(\sigma\), a large sample size can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(\frac{\sigma}{\sqrt{\text{n}} }\).
In this problem, we have that:
\(\mu=53,\sigma=21,\text{n}=49,\text{s}=\frac{21}{\sqrt{49} }=3\)The probability that the sample mean will be greater than 57.95
This is 1 subtracted by the p-value of Z when X = 57.95. So
\(Z=\dfrac{X-\mu}{\sigma}\)
By the Central Limit Theorem
\(Z=\dfrac{X-\mu}{\text{s}}\)
\(Z=\dfrac{57.95-53}{3}\)
\(Z=1.65\)
\(Z=1.65\) has a p-value of 0.9505.
Therefore, the probability that the sample mean will be greater than 57.95 is 1-0.9505 = 0.0495
To know more about the probability visit:
https://brainly.com/question/31321667
Graph the solution to this inequality on the number line.
−4m+3>11

Answers
Subtract numbers
-4m>11-3
Evaluate and subtract
-4m>8
Divide by -4
Solution
M<-2
Answer: The person above me is correct. Here is a picture if you still dont get it..
Step-by-step explanation:

Solve the equation 3(2x + 1)4- 16(2x + 1)² - 35 = 0 for x € R
Answers
The equation for x € R is \(x = (-1 ± √5) / 2 or x = (-1 ± √3) / (2√3).\)
Given equation is
3(2x + 1)4- 16(2x + 1)² - 35 = 0
To solve the given equation for x € R, we will use a substitution method and simplify the expression by considering (2x + 1) as p.
So the given equation becomes \(3p^4 - 16p^2 - 35 = 0\)
Let's factorize the given quadratic equation.
To find the roots of the given equation, we will use the product-sum method.
\(3p^4 - 16p^2 - 35 = 0\)
\(3p^4 - 15p^2 - p^2 - 35 = 0\)
\(3p^2(p^2 - 5) - 1(p^2 - 5) = 0\)
\((p^2 - 5)(3p^2 - 1) = 0 p^2 - 5 = 0\) or \(3p^2 - 1 = 0p^2 = 5 or p² = 1/3\)
Let's solve the equation for p now. p = ±√5 or p = ±1/√3
Let's substitute the value of p in terms of x.p = 2x + 1
Substitute p in the value of x.p = 2x + 1±√5 = 2x + 1 or ±1/√3 = 2x + 1x = (-1 ± √5) / 2 or x = (-1 ± √3) / (2√3)
Therefore, the solution of the equation 3(2x + 1)4- 16(2x + 1)² - 35 = 0 for x € R is x = (-1 ± √5) / 2 or x = (-1 ± √3) / (2√3).
Learn more about quadratic equation.
brainly.com/question/29269455
#SPJ11
SIMPLIFY OR COMBINE LIKE TERMS!!!
5ab^2- 12a^2b+ 3ab+ab^2+4a^2b

Answers
Answer:
Step-by-step explanation:

Find the other endpoint of the line segment with the given endpoint
and midpoint. Endpoint: (-9,-5) Midpoint: (-9,0)
PLEASE QUICK I CANT LEAVE THE ZOOM UNTIL I FINISH
Answers
Answer:
(-9,5)
Step-by-step explanation:
the midpoint occurs 5 units to the right of the endpoint. using this we can deduce that the other endpoint should also be 5 units right to the midpoint
Which table represents a linear function?


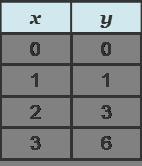

Answers
Step-by-step explanation:
the second table
......................
Which congruence postulate could prove TriangleAEM = TriangleDEN

Answers
Triangle AEM is congruent to triangle DEN by SAS congruence criterion.
What do you mean by congruence of triangle?
Triangle congruence: If all three corresponding sides and all three corresponding angles are equal in size, two triangles are said to be congruent. Slide, twist, flip, and turn these triangles to create an identical appearance. If moved, they coincide with one other. The sign of congruence is’ ≅’. After proving triangles congruent, the remaining dimension can be predicted without actually measuring the sides and angles of a triangle.
In triangle AEM and triangle DEN
AE = DE (Given)
ME = NE (As In triangle MEN , angle M = angle N and sides opposite to equal angles are equal)
angle MEA = angle NED (Vertically opposite angles)
Triangle AEM ≅ Triangle DEN (By SAS congruence criterion)
Therefore, both the trinagles are congruent by SAS congruence criterion.
To learn more about the congruence of triangle from the given link.
https://brainly.com/question/29268421
#SPJ1
Find the range and standard deviation of the set of data.4, 7, 4, 7, 7, 9, 11The range is(Simplify your answer.)

Answers
SOLUTI0N
Step 1 :
In this question, we are meant to find the range and standard deviation of the set of the data:
4, 7, 4, 7, 7, 9, 11
For the Range, we have that:
\(\begin{gathered} \text{Range = Highest number - Smallest number } \\ =\text{ 11 - 4} \\ =7 \end{gathered}\)Step 2 :
For the Standard Deviation,
We have that :
\(\text{Standard Deviation =}\frac{\sqrt[]{\sum ^{\infty}_{n\mathop=0}(X_{i\text{ }}-X)^2}}{n}\)So, we need to evaluate using the following process,
\(\begin{gathered} \text{Mean, X = }\frac{4\text{ + 7 + 4 + 7 +7 + 9 + 11}}{7} \\ =\frac{49}{7} \\ =\text{ 7} \end{gathered}\)Next, we evaluate the following :
Variance =
\(\frac{(4-7)^2+(7-4)^2+(4-7)^2+(7-7)^2+(7-7)^2+(9-7)^2+(11-7)^2}{7}\)=
\(\begin{gathered} \frac{9\text{ + 9 + 9 + 0 + 0 + 4 + 4}}{7} \\ =\text{ }\frac{35}{7} \\ =\text{ 5} \end{gathered}\)Next, we have that :
Standard Deviation =
\(\sqrt[\square]{Variance}\)=
\(\begin{gathered} \sqrt[\square]{5} \\ =\text{ 2. 236} \\ =\text{ 2. 2}4\text{ ( nearest hundredth )} \end{gathered}\)CONCLUSION:
The Range = 7 and the Standard Deviation = 2. 24
1. Determine if the lengths 9 cm, 13 cm, and 23 cm can form a triangle.
a. What are the two shortest side lengths?
acmt 15-24
b. Find the sum of the two shortest side lengths.
c. What is the longest side length?
d. Is the sum of the two shortest side lengths more than the length of the longest side?
e. Can the lengths 9 cm, 15 cm, and 23 cm form a triangle?
f. Fill in the blank so the three lengths will NOT form a triangle. 9 cm, 15 cm,
ст
2. Describe how to determine if three lengths form a triangle.

Answers
What is the smallest number or the number closest to 0
Find the derivative of the function. g(x)=
x
7
−2
x
2
−3x+2
Answers
The answer is 7x6-4x-3
Multiply: (6x - 1)(6x +1)
Answers
Answer:
36x^2 -1
Step-by-step explanation:
6x times 6x= 36x^2
6x times 1= 6x
-1 times 6x= -6x
-1 times 1= -1
so, ...
36x^2+6x+(-6x)+(-1) = 36x^2 -1
A local volunteer group is planning a family picnic. They ordered 175 hot dogs and
275 hamburgers. If they are planning for each person at the picnic to have one item
to eat, how many people will be attending?
Answers
Answer:
450 people
Step-by-step explanation:
Which number sentence is true? OA -6.8 (-1.3)=8.84 OB 6.8 (-1.3)=8.84 OQ-68.1.3=8.84 OD 6.8 1.3=-8.84
Answers
The true number sentence is the third option:
6.8*1.3 = 8.84
Which number sentence is true?
Here we have number sentences of the form:
A*B = C
This is true only when the value of the product A*B is equal to the value of C.
One key thing to identify the correct one is remembering the rule of signs:
(+)*(-) = (-)
(+)*(+) = (+)
(-)*(+) = (-)
(-)*(-) = (+).
The only option that meets that rule is:
6.8*1.3 = 8.84
Where the product of two positive numbers gives another positive number (and the equality is true) so we conclude that this number sentence is true.
If you want to learn more about number sentences:
https://brainly.com/question/2972832
#SPJ1
Find the direction angle of the vector v = 2i -6j
Answers
The direction angle of the vector v = 2i -6j is approximately 288.43 degrees.
What is a vector ?
In mathematics, a vector is a mathematical object that has both magnitude (length) and direction. Vectors are commonly used to represent physical quantities such as displacement, velocity, and force in physics and engineering, but they are also used in many other fields such as computer graphics, machine learning, and economics.
The direction angle of a vector is the angle it makes with the positive x-axis in the counterclockwise direction.
To find the direction angle, we first need to calculate the angle that the vector makes with the positive x-axis.
Using trigonometry, we can see that:
tan θ = (opposite side) / (adjacent side)
= (-6) / 2
= -3
Taking the inverse tangent of both sides, we get:
θ = tan⁻¹(-3)
Using a calculator, we find that:
θ ≈ -71.57°
However, since we are looking for the direction angle in the counterclockwise direction, we need to add 360 degrees to get the final answer:
θ = -71.57° + 360°
Thus, the direction angle of the vector v is approximately:
θ ≈ 288.43°
Therefore, the direction angle of the vector v = 2i -6j is approximately 288.43 degrees.
To learn more about Vector from given link.
https://brainly.com/question/29740341
#SPJ1
Will mark brainiest!
A factory makes memory cards. Workers test the quality of each batch of memory cards made in the factory. For testing purposes, 300 memory cards are selected at random from each batch. Of this sample, 8 memory cards are found to be broken. There are 5,000 memory cards in the batch. About how many memory cards in the batch are likely to be broken in all?
A, 133
B, 17
C, 400
D, 10

Answers
The expected number of memory cards in the batch that are likely to be broken is given as follows:
A. 133.
How to calculate a probability?A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.
8 out of 300 cards are broken, hence the probability that a single card is broken is given as follows:
p = 8/300.
Hence, the expected amount of broken cards out of 5000 cards is given as follows:
E(X) = 5000 x 8/300
E(X) = 133 cards.
More can be learned about probability at https://brainly.com/question/24756209
#SPJ1
Question 6(Multiple Choice Worth 2 points)
(Creating Graphical Representations LC)
A teacher was interested in the subject that students preferred in a particular school. He gathered data from a random sample of 100 students in the school and wanted to create an appropriate graphical representation for the data.
Which graphical representation would be best for his data?
Stem-and-leaf plot
Histogram
Circle graph
Box plot
Answers
The best graphical representation for the teacher's data on the subject preferences of 100 students in the school would be a histogram.
What is a histogram?The frequency or count of the data falling within each bin is represented by the height of a bar above the bin on the x-axis in a histogram, which is a graphical representation of the distribution of a set of continuous or discrete data. The histogram's y-axis displays the frequency or count of the data that falls into each bin.
A histogram would be the most effective visual depiction of the teacher's data on the preferred subjects of 100 students at the school. A histogram is a graphical representation of data where the frequency distribution of a set of continuous or discrete data is represented by bars.
Learn more about histogram here:
https://brainly.com/question/30354484
#SPJ1
If f(x)=6-2x, Find the value for f(-1)
Answers
Answer:
f(-1)=8
Step-by-step explanation:
Just plug in x=-1 into the function:
f(x)=6-2x
y=6-2(-1)
y=6+2
y=8
So f(-1)=8
Testing more properties of the Cobb-Douglas utility function Check if the Cobb-Douglas utility function u(x
1
,x
2
)=x
i
α
x
2
β
, where α,β>0, satisfies the following properties: (a) local nonsatiation, (b) decreasing marginal utility for both goods 1 and 2, (c) quasi-concavity, and (d) homotheticity.
Answers
The Cobb-Douglas utility function satisfies the properties of local non-satiation, decreasing marginal utility for both goods, quasi-concavity, and homotheticity.
The Cobb-Douglas utility function u(x1, x2) = xi^(α) * x2^(β), where α and β are both greater than zero, satisfies the following properties:
(a) Local non-satiation:
This property states that at each point of the consumption set, there is always another bundle that is arbitrarily close and strictly preferred. Thus, the function has local non-satiation.
(b) Decreasing marginal utility for both goods 1 and 2: The marginal utility of a good measures the utility obtained by consuming one more unit of it. The marginal utility of x1 can be obtained as:
MU1 = α * xi^(α−1) * x2^(β)
The marginal utility of x2 can be obtained as:
MU2 = β * xi^(α) * x2^(β−1)
Therefore, both marginal utilities are decreasing in x1 and x2, satisfying this property.
(c) Quasi-concavity:
The Cobb-Douglas function is quasi-concave. This means that the upper contour set of any level set of the function is convex. This can be proved by taking the second partial derivative of the function and checking whether it is negative or not.
(d) Homotheticity:
The Cobb-Douglas function is homothetic. This means that its shape is independent of the total level of utility. The proof can be achieved by checking whether the function is homogeneous of degree one or not. This is true, since multiplying the inputs by any positive scalar λ leads to a proportional increase in the output.
In conclusion, the Cobb-Douglas utility function satisfies all four properties - local non-satiation, decreasing marginal utility for both goods 1 and 2, quasi-concavity, and homotheticity.
Learn More About marginal utility from the below link:
https://brainly.com/question/15050855
#SPJ11
what is the area and yard of 15 and 4
Answers
Answer:
The area and yard is 60.
Step-by-step explanation:
15 x 4 = 60
Let me know if that helps!
Suppose professor nahele at the university of minnesota gave a quiz to 10 students. assume that it is possible to get a grade between 0 and 10 on the quiz.
Answers
The mean score has an equal probability of occurring of the scores in the uniformly distributed quiz is 5.5.
In a uniform distribution where the scores range from 1 to 10, each possible score has an equal probability of occurring. To find the mean (or average) of the scores, we can use the formula:
Mean = (Sum of all scores) / (Number of scores)
In this case, the sum of all scores can be calculated by adding up all the individual scores from 1 to 10, which gives us:
Sum of scores = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
The number of scores is 10 since there are 10 possible scores from 1 to 10.
Plugging these values into the formula, we get:
Mean = 55 / 10 = 5.5
Therefore, the mean of the scores in this quiz is 5.5.
Learn more about the probability at
https://brainly.com/question/31828911
#SPJ4
The question is -
Suppose a professor gave a quiz where the scores are uniformly distributed from 1 to 10. What is the mean of the scores?
a student was asked to find the equation of the tangent plane to the surface at the point . the student's answer was (a) at a glance, how do you know this is wrong. what mistakes did the student make? select all that apply. a. the answer is not a linear function. b. the (x - 5) and (y - 4) should be x and y. c. the partial derivatives were not evaluated a the point. d. the -131 should not be in the answer. e. all of the above (b) find the correct equation for the tangent plane.
Answers
The answer is not a linear function, and the evaluation of the partial derivatives was done to a point. Thus, options (a) and (c) are correct. The correct equation for the tangent plane is z = 3x - 108y - z + 241 = 0.
In a given point (x₀, y, z₀) the equation of the tangent plane to a surface given by the function S = f(x, y)can be obtained by
z-z₀ = f ₓ (x₀, y₀, z₀) (x - x₀) + fᵧ (x₀, y₀, z₀) (y - y₀) ... (i)
where f ₓ (x₀, y₀, z₀) and fᵧ (x₀, y₀, z₀) (y - y₀) are the partial derivatives of f(x, y) with respect to x and y respectively. These two derivatives are evaluated at the point (x₀, y₀, z₀) .
Thus, we need to find two missing inputs, the z₀ coordinate and the two partial derivatives, in our problem in order to use equation (i).
In the case of z₀, evaluation of the given function gives us z = -80.
The partial derivatives are thus-
δf(x,y) / δx = fₓ (x, y) = 3x²
fₓ (x₀, y₀) = fₓ (1, 3) = 3
δf(x,y)/δxy= fᵧ (x, y) = -4y³
fᵧ (x₀, y₀) = fᵧ (1, 3) = -108
Now, arranging these values in equation (i) we obtain:
z-z₀ = f ₓ (x₀, y₀, z₀) (x - x₀) + fᵧ (x₀, y₀, z₀) (y - y₀)
z +80 = 3x² (x -1) - 4y³ (y - 3)
z = -80 +3x² (x -1) - 4y³ (y - 3)
Now, we will substitute the values of the partial derivatives at the given point:
z = -80 + 3x² (x -1) - 4y³ (y - 3)
z = 3x² (x -1) - 108 (y - 3)
z = 241 + 3x -108y
i.e., 3x - 108y - z + 241
Thus, the correct equation is 3x - 108y - z + 241.
Learn more about linear functions:
brainly.com/question/15602982
The complete question is-
A student was asked to find the equation of the tangent plane to the surface z = x³−y⁴ at the point (x, y) = (1, 3). The student's answer was z = −80 + 3x²(x−1)−(4y³)(y−3).
(a) At a glance, how do you know this is wrong? What mistakes did the student make? Select all that apply. A. The (x - 1) and (y - 3) should be x and y. B. The -80 should not be in the answer. C. The partial derivatives were not evaluated at this point. D. The correct answer is not a linear function. E. All of the above.
(b) What is the correct equation for the tangent plane? z=
#SPJ4
use the appropriate normal distribution to approximate the resulting binomial distributions. a fair coin is tossed 130 times. what is the probability of obtaining between 55 and 69 tails, inclusive? a) 0.7523 b) 0.7134 c) 0.7221 d) 0.7179 e) 0.7494 f) none of the above.
Answers
The probability is 0.6962 for the given standard deviation.
What is standard deviation?
Standard Deviation is a measure that shows what quantity variation (such as unfold, dispersion, spread,) from the mean exists. the quality deviation indicates a “typical” deviation from the mean. it's a well-liked live of variability as a result of it returns to the first units of live of the info set.
Main body:
X - Binomial(n = 130, p = 0.5)
Binomial can be approximated to normal with: μ = np = 130*0.5 = 65
σ = √np(1 − p) - = √130* (0.5)(1 − 0.5)
σ = 5.7
P(55 ≤ X ≤ 69 )
Since we are approximating a discrete binomial distribution by continuous normal distribution, values between 54.5 and 68.5 both approximate to 55. Thus, "between 55 and 69" corresponds to continuous normal distribution with P(54.5 < X 68.5) after continuity correction.
Normal Distribution, x₁ = 54.5, x2 = 68.5, µ = 65, σ = 5.7
We convert this to standard normal using z =
z₁ = 54.5-65/ 5.7 ≈ - 1.84
z₂ = 68.5-65/ 5.7 ≈ 0.614
P(54.5 < X < 68.5) = P(- 1.84 < Z < 0.614)
= P(Z < 0.614) − P(Z <- 1.84)
= 0.7291 - 0.0329 (from z-table)
= 0.6962
Hence the probability is 0.6962
To know more about standard deviation , visit:
brainly.com/question/475676
#SPJ4
If the allele frequency of the dominant allele is 0.4, what value is used for the term p^2 in the equation p^2+ 2pq + q^2 = 1?
Answers
The value is used for the term p^2 in the equation p^2+ 2pq + q^2 = 1 is 0.16.
According to the statement
we have given that the allele frequency of the dominant allele is 0.4, and we have to find that the value of p^2 in the equation p^2+ 2pq + q^2 = 1.
So, For this purpose, we know that the
The allele frequency represents the incidence of a gene variant in a population. Alleles are variant forms of a gene that are located at the same position, or genetic locus, on a chromosome.
And here
allele frequency is the 0.4 and represent the value of P.
So, The value of p is 0.4 and the
Then p^2 = (0.4)^2
so, the value becomes
p^2 = (0.4)^2
p^2 = 0.16.
So, The value is used for the term p^2 in the equation p^2+ 2pq + q^2 = 1 is 0.16.
Learn more about allele frequency here
https://brainly.com/question/6139888
#SPJ4
PLEASE HELP NOW
Alex's weekly earnings for working 40 hours plus 3 hours of working overtime was $480.17. If
$48.57 of that paycheck was overtime pay, what was his hourly rate for the first 40 hours of
work?
$10.04
$10.79
O$11.17
$12.00
Answers
Answer:
$10.79
Step-by-step explanation:
1) Make an equation
40x + 48.67 = 480.17
where x is hourly pay
2) Solve
40x + 48.67 = 480.17
40x + 48.67 - 48.67 = 480.17 - 48.67
40x = 431.50
40x / 40 = 431.50 / 40
x = 10.79
Help pls and explain!!

Answers
Answer: 15 minutes
Step-by-step explanation:
Answer:
15 minutes is your answers
The function is defined by f(x)=x^2+6

Answers
Answer: \(9x^2 +6\)
Step-by-step explanation:
\(f(3x)=(3x)^2 +6=9x^2 +6\)
A researcher records the following scores on a working memory quiz for two samples. Which sample has the largest standard deviation?
Sample A: 2, 3, 4, 5, 6, 7, and 8
Sample B: 4, 5, 6, 7, 8, 9, and 10
Sample A
Sample B
Both samples have the same standard deviation.
Answers
A researcher records the following scores on a working memory quiz for two samples. Sample B has the largest standard deviation.
To determine which sample has the largest standard deviation, we need to calculate the standard deviation for both samples. Here are the steps to calculate the standard deviation:
1. Find the mean (average) of each sample.
2. Calculate the difference between each score and the mean.
3. Square the differences.
4. Find the mean of the squared differences.
5. Take the square root of the mean of the squared differences.
Sample A:
1. Mean: (2+3+4+5+6+7+8)/7 = 5
2. Differences: -3, -2, -1, 0, 1, 2, 3
3. Squared differences: 9, 4, 1, 0, 1, 4, 9
4. Mean of squared differences: (9+4+1+0+1+4+9)/7 = 28/7 = 4
5. Standard deviation: √4 = 2
Sample B:
1. Mean: (4+5+6+7+8+9+10)/7 = 7
2. Differences: -3, -2, -1, 0, 1, 2, 3
3. Squared differences: 9, 4, 1, 0, 1, 4, 9
4. Mean of squared differences: (9+4+1+0+1+4+9)/7 = 28/7 = 4
5. Standard deviation: √4 = 2
Both samples have the same standard deviation of 2.
Learn more about Samples:
brainly.com/question/12823688
#SPJ11