There are two twins. One twin wants to explore the planet near Proxima Centauri and leaves on a spaceship traveling at 90% of the speed of light, while the other twin stays home on Earth. How much does the twin on Earth age while the other twin travels to Proxima Centauri?
Answers
Answer:
4.7 years
Step-by-step explanation:
Distance of planet from Earth = 1.3 parsec
We know that 1 parsec = 3.26 light years
And a light year is the distance traveled by light in time period of 1 year.
So, Distance of planet from Earth = 1.3 \(\times\) 3.26 = 4.24 light years
Given that, the person travels at a speed equal to 90% of the light speed.
To travel to the planet from Earth, Light takes 4.24 years.
To travel the distance \(D\), at a speed \(s\) light takes time of 4.24 years.
To travel the distance \(D\), at a speed \(0.90s\), the person takes time:
\(\dfrac{4.24}{0.90} = \bold{4.7\ years}\)
So, the twin on Earth ages by 4.7 years.
Answer:
4.7 years
Step-by-step explanation:
Related Questions
In the balance sheet, mortgage notes payable are reported as both a current and a long-term liability. a current liability only. a current liability except for the reduction in principal amount. a long-term liability only.
Answers
In the balance sheet, mortgage notes payable are reported as a long-term liability only.
Mortgage notes payable represent the amount owed by a company for a mortgage loan. These loans are typically long-term obligations that are expected to be repaid over an extended period, often several years. Therefore, mortgage notes payable are classified as long-term liabilities in the balance sheet.
Current liabilities are obligations that are expected to be settled within a short period, usually one year or less. Since mortgage notes payable typically have a longer repayment term, they do not meet the criteria to be classified as current liabilities.
By reporting mortgage notes payable as a long-term liability, the balance sheet provides a clear distinction between the company's short-term and long-term obligations, helping stakeholders understand the company's financial position and obligations over different time horizons.
To learn more about balance sheet click here: brainly.com/question/28446946
#SPJ11
4. "Working from Whole to Part" is the major principles of Land Surveying, using simple sketches discuss how you understand this principle ( 15mks ).
Answers
The "working from whole to part" principle involves surveying a particular area first, creating a scaled map and identifying key features, then breaking down the land into smaller sections. Sketches are essential for this principle.
The “working from whole to part” principle is one of the major principles of Land Surveying. It involves surveying a particular area first before moving on to the specifics. This involves creating a scaled map of the whole land and identifying the key features that must be surveyed. This can be achieved through a series of sketching, which involves drawing to-scale images of the whole area. Once the whole part has been established, the surveyor then moves on to the specifics, where the land is broken down into smaller sections that are easier to manage.
Sketches are an essential part of this principle, and they help the surveyor to identify the key features of the land that are to be surveyed.
To know more about survey of land Visit:
https://brainly.com/question/31082518
#SPJ11
find the root of 6x^2+13×+6=0 using graphical method of quadratic equation
Answers
Answer....
Ok done. Thank to me >:33

Viyan age is 2 / 5 of the age of her eldest brother. If his brother's age is 35 years, then how old is viyan?
Answers
A cotton candy vendor has 27 cones of blue cotton candy to sell. If the blue cotton candy is 75% of the total number of cones, how many total cotton candy cones does he have?
Answers
Answer:
36
Step-by-step explanation:
Let the total number of cotton candy = A
Number of blue cotton candy = 27 cones
Percentage of blue cotton candy = 75%
Therefore, the total number of cotton candy is calculated as:
27/A × 100 = 75%
2700/A = 75
Cross Multiply
75A = 2700
A = 2700/75
A = 36
Therefore, the amount of total cotton candy that we have is 36.
I need help
Solving this problem

Answers
The required value of x is 22 degrees for the given figure.
Adjacent angles are a sort of additional angle. Adjacent angles share a common side and vertex, such as a corner point. Their points do not overlap in any manner.
As we know that supplementary angles are defined as when pairing of angles addition to 180° then they are called supplementary angles.:
According to the given figure, it can be written as follows:
2x + 24 + 6x - 20 = 180
8x + 4 = 180
8x = 180 - 4
8x = 176
x = 176/8
x = 22
Therefore, the required value of x is 22 degrees for the given figure.
Learn more about supplementary angles here:
brainly.com/question/3027144
#SPJ1
The complete question is as follows:
Find the value of x for the below figure.

a 7000 liter vat is filled with a mixture containing 20% orange juice. determine the number of liters of this mixture that must be drained away and replace with a 80% orange juice mixture to obtain an overall mixture of 7000 liters containing 25% orange juice
Answers
We need to drain away 1750 liters of the 20% orange juice mixture and replace it with an 80% orange juice mixture.
To solve this problem, we need to use the equation:
(initial amount of orange juice in vat - amount drained + amount added) / final amount of mixture = desired percentage of orange juice
Let's start by finding the initial amount of orange juice in the vat. We know that the vat contains 7000 liters of mixture, and 20% of that is orange juice:
Initial amount of orange juice = 7000 liters x 0.20 = 1400 liters
Next, we need to find the amount of mixture that must be drained away. Let's call this amount "x". We know that we want to replace this with an 80% orange juice mixture, so we can set up the following equation:
(1400 - x + 0.8x) / 7000 = 0.25
Simplifying this equation:
(1400 + 0.2x) / 7000 = 0.25
1400 + 0.2x = 1750
0.2x = 350
x = 1750
Therefore, we need to drain away 1750 liters of the 20% orange juice mixture and replace it with an 80% orange juice mixture.
Know more about mixture here,
https://brainly.com/question/24898889
#SPJ11
Select the values that make the inequality -- m > -7 true.
Then write an equalivalent inequality, in terms of m.
(Numbers written in order from least to greatest going across.)

Answers
Equivalent inequality: m < 7
An equivalent inequality, in terms of m is m<7.
The given inequality is -m>-7.
We need to write an equivalent inequality in terms of m for the given inequality.
What is an equivalent inequality?Equivalent inequalities are inequalities with the same solutions. They're also the most likely to get paired up together on eHarmony. It's incredible how much they have in common. It's like they were made for each other.
Now, -12, -8 and -7.1 values make the given inequality true.
Multiply -1 on both the sides of inequality -m>-7.
That is, -m(-1)<-7(-)
⇒m<7
Therefore, an equivalent inequality, in terms of m is m<7.
To learn more about an equivalent inequality visit:
https://brainly.com/question/28370368.
#SPJ2
On a treasure map, the actual distance varies
directly to the scaled distance. If 15 actual
miles is represented by 3 centimeters on the
map, then how many centimeters on the map
are equivalent to 135 actual miles?
Answers
Answer:27
Step-by-step explanation:
miles =m cm= c m/c= answer
15/3=5
135/5=27
A line passes through the point (-9,1) and has a slope of -2/3
Answers
Answer:
y - 1 = (-2/3)(x + 9)
Step-by-step explanation:
Here you are given a point on a line and the slope of the line. You'll need to apply the "point-slope" formula
y - k = m(x - h) (Memorize this)
Then m = slope = -2/3, h = -9 and k = 1.
Making the appropriate substitutions, we get:
y - 1 = (-2/3)(x + 9)
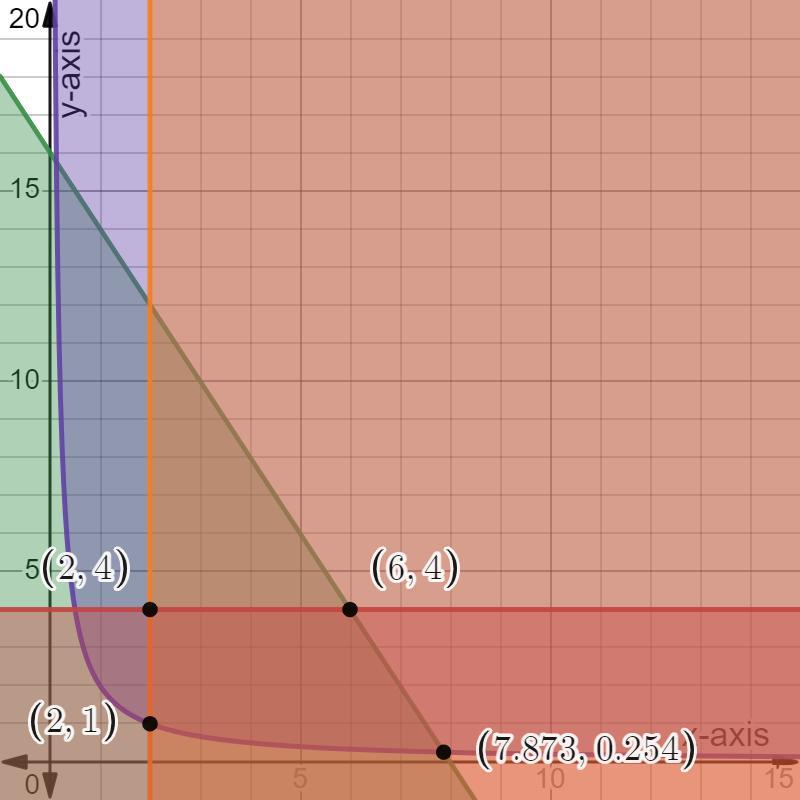
4. Solve the problem given with the constrains and objective function. Maximize profit 30X, + 40X2 Subject to; 4X₁ + 2X₂ ≤ 32
2X₁ X₂ ≥ 4 X₁ ≥ 2 X₂ ≤ 4
Answers
The maximum profit is 340, and it occurs when X₁ = 6 and X₂ = 4.
The objective is to maximize the profit function 30X₁ + 40X₂, subject to the following constraints:
4X₁ + 2X₂ ≤ 32
2X₁X₂ ≥ 4
X₁ ≥ 2
X₂ ≤ 4
Let's break down the steps to solve the problem:
Step 1: Graph the feasible region:
Plot the equations 4X₁ + 2X₂ = 32, 2X₁X₂ = 4, X₁ = 2, and X₂ = 4 on a coordinate plane.
Shade the feasible region that satisfies all the constraints.
Step 2: Identify the corner points and evaluate the profit:
1. For the point (2, 4):
Profit = 30(2) + 40(4) = 60 + 160 = 220
2. For the point (6, 4):
Profit = 30(6) + 40(4) = 180 + 160 = 340
3. For the point (7.873, 0.254):
Profit = 30(7.873) + 40(0.254) = 236.19 + 10.16 = 246.35
4. For the point (2, 1):
Profit = 30(2) + 40(1) = 60 + 40 = 100
Comparing the profits obtained at each corner point, we find that the maximum profit is achieved at the point (6, 4), which yields a profit of 340.
Therefore, the maximum profit is 340, and it occurs when X₁ = 6 and X₂ = 4.
To know more about maximum profit, refer here:
https://brainly.com/question/17200182
#SPJ4
WILL MARK BRAINLIEST PLEASE HELP ME! In a complete sentence, describe the angle relationship between ∠APD and ∠CPB. Then write and solve an equation based on the relationship you identified in order to find the measure of ∠APD.

Answers
Answer:
∠APD and ∠CPB are Vertical Angles
Equation: 6x - 10 = 4x + 8
Step-by-step explanation:
We use the Vertical Angles Theorem to solve for x:
Step 1: Set up equation
6x - 10 = 4x + 8
Step 2: Subtract 4x on both sides
2x - 10 = 8
Step 3: Add 10 to both sides
2x = 18
Step 4: Find x by dividing 2 on both sides
x = 9
Step 5: Plug in x for 9 to find degree measure
m∠CPB = 4(9) + 8
m∠CPB = 36 + 8
m∠CPB = 44°
m∠CPB = m∠APD (Vertical Angles)
m∠APD = 44°
Answer:
\(\boxed{\mathrm{view \: explanation}}\)
Step-by-step explanation:
∠APD and ∠CPB are vertically opposite angles
The equation is 6x-10=4x+8
\(6x-10=4x+8\\6x-4x=8+10\\2x=18\\x=9\)
Plug x as 9 for the angle.
\(4(9)+8\\36+8\\44\)
∠APD and ∠CPB = 44 degrees
26. Which is larger?
A. 1tsp
B. 1tbsp.
Answers
Answer:
B. 1tbsp
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
I tbsp is always larger than 1tsp
James has a sidewalk that runs through his flower garden. He needs to put more mulch in the flower garden. If one bag of mulch covers 4 square yards, how many bags of mulch will he need?
Answers
Answer:
See Explanation
Step-by-step explanation:
Given
The given proportion can be represented as:
\(1\ bag = 4yd^2\)
Required
The additional number of mulch needed
The question has incomplete details, as the amount of mulch he has applied and the area of the flower garden are not given.
So, I will make some assumptions to solve this question.
Let the area of his flower garden be x.
So, we have:
\(1\ bag = 4yd^2\)
\(y = x\ yd^2\)
Cross multiply
\(4yd^2 * y = xyd^2 * 1\ bag\)
Make y the subject
\(y = \frac{x\ yd^2 * 1\ bag}{4yd^2}\)
\(y = \frac{x* 1\ bag}{4}\)
\(y = \frac{x}{4}\ bag\) --- This represents the total amount of mulch required for the flower garden
--------------------------------------------------------------------------------------------------------
Assumptions
Assume that \(x = 16\),
So, we have:
\(y = \frac{x}{4}\ bag\)
\(y = \frac{16}{4}\)
\(y = 4\)
i.e 4 bags are needed.
Assume he has applied 2 bags already.
The number of bags needed to apply will be:
\(y - 2\)
\(y - 2 = 4 - 2\)
\(y - 2 = 2\)
2 more bags needed
--------------------------------------------------------------------------------------------------------
Jacqueline bought a bicycle at wholesale cost for $210 dollars. If the bicycle is normally $300 from the local bike shop, what is the percent markup the bike shop adds to the wholesale cost?
Answers
If Jacqueline bought a bicycle at wholesale cost for $210 dollars. If the bicycle is normally $300 from the local bike shop, Then 30% markup the bike shop adds to the wholesale cost
What is Percentage?Percentage, a relative value indicating hundredth parts of any quantity.
Given,
Jacqueline bought a bicycle at wholesale cost for $210 dollars.
The actual price of bicycle is normally $300 from the local bike shop.
We need to find the percent markup the bike shop adds to the wholesale cost.
For this we need to find the difference and we have to divide it by actual price
300-210/300=90/300=0.3
Now multiply 0.3 with 100 as hundredths to get the percentage value
0.3×100=30
Hence 30 percent markup the bike shop adds to the wholesale cost
To learn more on Percentage click:
https://brainly.com/question/28269290
#SPJ1
The model represents an inequality. What is the solution set for the inequality?
F). x ≤ -5
G). x ≤ 5
H). x ≤ 1
J). x ≤ -14

Answers
Answer:
-5
Step-by-step explanation:
4x+12 is less than or equal to -8 so subtract 12 from -8 and get -20 so 4x is less than or equal to -20 then divide -20 by 4 and get -5
Your client is 25 years old, and she wants to begin saving for retirement, with the first payment to come one year from now. She can save $3,500 per year, and you advise her to invest it in securities which you expect to provide an average annual return of 7 percent. If she follows your advice, how much money would she have at age 70?
Answers
Given data: Principal amount (P) = $3,500Number of years (t) = 70 - 26 = 44 years. Rate of Interest (R) = 7%Total amount that client will have after 44 years can be calculated as follows: Total Amount (A) = P[(1 + R/100)^t - 1]/(R/100)Putting the values:
Therefore, Total Amount (A) = $3,500[(1 + 7/100)^44 - 1]/(7/100)Total Amount (A) = $680,471.44Therefore, client will have $680,471.44 at the age of 70 years.
If the client saves $3,500 per year and invests in securities that provide an average annual return of 7 percent, she will have $680,471.44 by the time she reaches the age of 70. Since the first payment will be made one year from now, the amount of money that will accumulate will be for 44 years (70-26). The formula for calculating the total amount that the client will have after 44 years can be derived as follows:
Total Amount (A) = P[(1 + R/100)^t - 1]/(R/100)Where P is the principal amount, R is the rate of interest, and t is the number of years. The value of P is given as $3,500, and the rate of interest is 7 percent. Putting these values in the above equation, we get:
Total Amount (A) = $3,500[(1 + 7/100)^44 - 1]/(7/100)The total amount that the client will have after 44 years is $680,471.44. Therefore, it is advisable for the client to save $3,500 per year and invest it in securities that provide an average annual return of 7 percent. This investment plan will help the client to accumulate a substantial amount of money for her retirement.
Thus, the client can have $680,471.44 by the time she reaches the age of 70 if she saves $3,500 per year and invests it in securities that provide an average annual return of 7 percent. This investment plan will help the client to accumulate a substantial amount of money for her retirement.
To know more about Rate of Interest :
brainly.com/question/14556630
#SPJ11
Paul is making the table below to show equivalent numbers of kilograms and grams. What is one of the missing numbers in Paul's table? 14,000 20,000 Number of Grams Number of Kilograms 2 14 200 ? ? 1,400
Answers
Answer:
Answer is 14,000
Step-by-step explanation:
U have to do 14x1000 because each kilo To gram is 1000 so the answer is 14,000
Answer:
Step-by-step explanation:
14,000
The volume of a cylinder is 725x cm”. The radius of the base of the cylinder is 5 cm. What is the height of the cylinder?
Answers

9=4/t Math Answer 6th grade problem
Answers
9=4/t
To solve for t
multiply both-side of the equation by t
That is;
\(9\times t=\frac{4}{t}\times t\)9t = 4
divide both-side of the equation by 9
That is;
\(\frac{9t}{9}\text{ =}\frac{4}{9}\)\(t=\frac{4}{9}\)The Drama Club is selling tie-dye T shirts as fundraiser. They buy the dyeing materials for $60 and white t-shirts for $2. 50 each. They sell the finished shirts for $10 each. Write an equation in y=mx+b form
Answers
The equation can be model in this form y = mx + b:
y = 2.5x + 60
Linear equation:y = mx + b
where
m = slope
b = y-intercept
Therefore, let model the situation into a linear equation.
y = total cost of the T-shirts
x = number of T-shirt made
b = $60
Therefore, the equation can be model in this form y = mx + b as follows:
y = 2.5x + 60learn more on linear equation here: https://brainly.com/question/22218249
The table shows the membership cost for two CD clubs. How many CDs would you need to buy in a year in order for the total cost of both memberships to be the same?
CD Club Membership
Club #1: Annual Fee = 50$ and Cost Per CD = 7.50$
Club #2: Annual Fee = 35$ and Cost Per CD = 8.00$
Answers
Answer:
Club 1: 16 would be 120
Club 2: 15 would be 120
The number of milligrams D (ht) of a certain drug that is in a patient's bloodstream h hours after the drug is injected is given by the following function.
D(h) = 25e -0. 4
When the number of milligrams reaches 6, the drug is to be injected again. How much time is needed between injections?
Round your answer to the nearest tenth, and do not round any intermediate computations.
Answers
The time is needed between injections is 3.6 hours, i.e., the drug is to be injected again when the number of milligrams reaches 6 mg.
We have the exponential function of number of milligrams D (ht) of a certain drug that is in a patient's bloodstream h hours after the drug is injected is
\(D(h)=25 {e}^{ - 0.4 h}\)
We have to solve for h (the numbers of hours) that would have passed when the D(h) (the amount of medication in the patient's bloodstream) equals 6 mg in order to know when the patient needs to be injected again.
\(6 = 25 {e}^{ - 0.4h} \)
\( \frac{6}{25} = \frac{25}{25} {e}^{ - 0.4h} \)
\(0.24= {e}^{ - 0.4h} \)
Taking logarithm both sides of above equation , we get,
\( \ln(0.24) = \ln( {e}^{ - 0.4h)} \)
Using the properties of natural logarithm,
\( \ln(0.24) = - 0.4h\)
\( - 1.427116356 = - 0.4h\)
\(h = \frac{1.42711635}{0.4} = 3.56779089\)
=> h = 3. 6
So, after 3.6 hours, the patient needs to be injected again.
To learn more about exponential function, refer:
https://brainly.com/question/2456547
#SPJ4
Simplify (square root)2/^3(square root)2
A. 2^1/6
B. 2^1/3
C. 2^5/6
D. 2^3/2

Answers
Answer: Personally I would do option "B" 2 1/3 because it sounds right.
For a certain type of hay fever, Medicine H has a 30% probability of working. In which distributions does the variable X have a binomial distribution?
Select EACH correct answer.
A. When the medicine is tried with two patients, X is the number of patients for whom the medicine worked.
B. When the medicine is tried with six patients, X is the number of patients for whom the medicine does not work.
C. When the medicine is tried with six patients, X is the number of patients for whom the medicine worked.
D. When the medicine is tried with two patients, X is the number of doses each patient needs to take.
Answers
The variable X has a binomial distribution in the following distributions:
A. When the medicine is tried with two patients, X is the number of patients for whom the medicine worked.
C. When the medicine is tried with six patients, X is the number of patients for whom the medicine worked.
What is binomial distribution?In a binomial probability distribution, the number of "Successes" in a series of n experiments is represented as either success/yes/true/one (probability p) or failure/no/false/zero (probability q = 1 p), depending on the outcome's boolean value.
In a binomial distribution, we have a fixed number of independent trials (in this case, the number of patients), and each trial has only two possible outcomes (success or failure). The probability of success remains the same for each trial (in this case, the probability of the medicine working is 30%).
Option B does not represent a binomial distribution since it counts the number of patients for whom the medicine does not work, which is the complement of success. Option D is not a binomial distribution as it counts the number of doses each patient needs to take, which is not a success/failure outcome.
So, the correct answers are:
A. When the medicine is tried with two patients, X is the number of patients for whom the medicine worked.
C. When the medicine is tried with six patients, X is the number of patients for whom the medicine worked.
Learn more about binomial distribution on:
https://brainly.com/question/29137961
#SPJ4
Jack is a discus thrower and hopes to make it to the Olympics some day. He has researched the distance (in meters) of each men's gold medal discus throw from the Olympics from 1920 to 1964. Below is the equation of the line of best fit Jack found.
y= 0.34x + 44.63
When calculating his line of best fit, Jack let x represent the number of years since 1920 (so x=0 represents 1920 and x=4 represents 1924).
Using the line of best fit, estimate what the distance of the gold medal winning discus throw was in 1980.
a. 71.83 meters
b. 717.83 meters
c. 44.63 meters
d. 65.03 meters
Answers
Answer:
d. 65.03 meters
Step-by-step explanation:
The line of best fit, for the distance of the winning throw, in x years after 1980 is:
Using the line of best fit, estimate what the distance of the gold medal winning discus throw was in 1980.
1980 - 1920 = 60, so this is y(60).
So the answer is 65.03 meters.
Explain why there are an infinite number of angles that are coterminal to a certain angle. a) Angles that are not in standard position can have their initial side located at any angle.b) There are an infinite number of angles between 0∘ and 360∘.c)The digits of π continue infinitely. There is an angle measure corresponding to each digit.d) Coterminal angles can be found by adding any positive or negative multiple of 360∘. There are an infinite number of multiples. e) Angles that are not in standard position can have their terminal side located at any angle.
Answers
The correct answer is (d) Coterminal angles can be found by adding any positive or negative multiple of 360°. There are an infinite number of multiples.
Coterminal angles are angles that have the same initial and terminal sides. They can be obtained by adding or subtracting any positive or negative multiple of 360° to the given angle. Since 360° represents one full revolution around a circle, adding or subtracting multiples of 360° will bring us back to the same position, resulting in angles that are coterminal.
For example, let's consider an angle of 45°. By adding 360° to it, we get 405°, which is coterminal to 45°. Similarly, subtracting 360° from 45° gives us -315°, which is also coterminal. We can continue this process indefinitely, adding or subtracting multiples of 360° to find an infinite number of coterminal angles.
Therefore, the fact that there are an infinite number of multiples of 360° allows us to find an infinite number of angles that are coterminal to a certain angle. This is the reason why option (d) is the correct explanation for why there are an infinite number of coterminal angles.
Learn more about Coterminal angles here:
https://brainly.com/question/23093580
#SPJ11
1/8b as a verbal expression
Answers
Answer:
one eighth of a number b
Step-by-step explanation:
Answer:
one eighth of a number b
Step-by-step explanation:
Please answer in an hour! You will get a thumbs up.
Question 1 (a)
Assume you purchase a new tractor on Jan 1, 2022 for a cost of $200,000. You estimate you will be able to use the tractor for 10 years, and it will have a salvage value of 10% of the original by the end of its useful life. Determine the book value at the end of the first year (December 31, 2022) using straight-line depreciation.
options:
$18,000
$180,000
$185,000
$182,000
Question 1 (b)
A balance sheet (using current and noncurrent assets and liabilities- no intermediate) shows that a farmer has current assets of $80,000 and owner equity of $100,000. Her current ratio is 2 and her debt/equity ratio is 1.0. Determine the farmer's noncurrent liabilities.
Question 1 (b) options:
$40,000
$60,000
$100,000
unable to determine
Answers
Question 1a
To calculate the book value at the end of the first year using straight-line depreciation, we need to determine the annual depreciation expense first. The straight-line method assumes that the asset depreciates by an equal amount each year over its useful life. Therefore, we can use the following formula to calculate the annual depreciation:
Annual Depreciation = (Cost - Salvage Value) / Useful Life
Substituting the given values, we get:
Annual Depreciation = ($200,000 - $20,000) / 10 years = $18,000 per year
This means that the tractor will depreciate by $18,000 each year for the next 10 years.
To determine the book value at the end of the first year, we need to subtract the depreciation expense for the year from the original cost of the tractor. Since one year has passed, the depreciation expense for the first year will be:
Depreciation Expense for Year 1 = $18,000
Therefore, the book value of the tractor at the end of the first year will be:
Book Value = Cost - Depreciation Expense for Year 1
= $200,000 - $18,000
= $182,000
So the book value of the tractor at the end of the first year, December 31, 2022, using straight-line depreciation is $182,000. so the answer is D
Question 1(b)
To determine the farmer's noncurrent liabilities, we need to use the information provided to calculate the total liabilities and then subtract the current liabilities from it. Here's the step-by-step solution:
Calculate the total current liabilities using the current ratio:
Current Ratio = Current Assets / Current Liabilities
2 = $80,000 / Current Liabilities
Current Liabilities = $80,000 / 2
Current Liabilities = $40,000
Calculate the total liabilities using the debt/equity ratio:
Debt/Equity Ratio = Total Liabilities / Owner Equity
1.0 = Total Liabilities / $100,000
Total Liabilities = $100,000 * 1.0
Total Liabilities = $100,000
Subtract the current liabilities from the total liabilities to get the noncurrent liabilities:
Noncurrent Liabilities = Total Liabilities - Current Liabilities
Noncurrent Liabilities = $100,000 - $40,000
Noncurrent Liabilities = $60,000
Therefore, the farmer's noncurrent liabilities are $60,000. so the answer is B.
Savannah made two posters. The second poster was 3 times larger than the first. If the first poster was 78 square inches, how large were the posters altogether?
Answers
Answer: 312 square inches
Step-by-step explanation:
Given: The first poster was 78 square inches.
Also, The second poster was 3 times larger than the first.
The area of second poster = 3 x (First poster)
= 3 x (78) square inches
= 234 square inches
The area of both posters = Area of first poster + Area of second poster
= (78+234) square inches
= 312 square inches
Hence, the posters were 312 square inches large altogether.