There are approximately 26 billion ounces of a water left in a natural spring, and every year humans consume about 150 million ounces of it. Let V stand for the volume (in millions of ounces) of spring water remaining, and t stand for the number of years since 2018. What linear equations could model the decreasing supply of water in this particular spring?

Answers
Answer:
V(t) = 26,000 - 15t
Step-by-step explanation:
Given the following :
Initial approximate volume of water = 26 billion ounces
Yearly consumption = 150 million ounces
Let V = volume remaining
Linear equation to model decreasing supply of water.
Volume left = Initial volume - consumption
Consumption = 150 million per year
Consumption after t years = 150 million * t
Volume left = 26,000,000,000 - 150,000,000t
V = 26,000,000,000 - 150,000,000t
Divide by 1,000,000
V(t) = 26,000 - 15t
Related Questions
Acme T-Shirt Company charges a $50 set-up fee plus $9 for each shirt printed. Beta T-shirt Company has no set up fee, but charges $14 per shirt. What is the minimum number of shirts for which a customer saves money by using Acme?
Answers
Answer:
Step-by-step explanation:
Acme Company:
Let the number of shirts = x
Cost = 50 + 9x
Beta Company:
Cost = 14x
50 + 9x < 14x
Subtract 9x from both sides
50 < 14x - 9x
50 < 5x
Divide both sides by 5
50/5 < x
10 < x
Minimum number of shirts for which a customer saves money by using Acme = 11 T-shirts
write the first five terms of the sequence with the given nth term. an = − 4 5 n
Answers
the first five terms of the sequence are:
-4/5, -8/5, -12/5, -16/5, -4
To find the first five terms of the sequence with the nth term given by an = -4/5n, we substitute the values of n from 1 to 5 into the nth term expression.
For n = 1:
a1 = -4/5(1) = -4/5
For n = 2:
a2 = -4/5(2) = -8/5
For n = 3:
a3 = -4/5(3) = -12/5
For n = 4:
a4 = -4/5(4) = -16/5
For n = 5:
a5 = -4/5(5) = -20/5 = -4
To know more about sequence visit:
brainly.com/question/30262438
#SPJ11
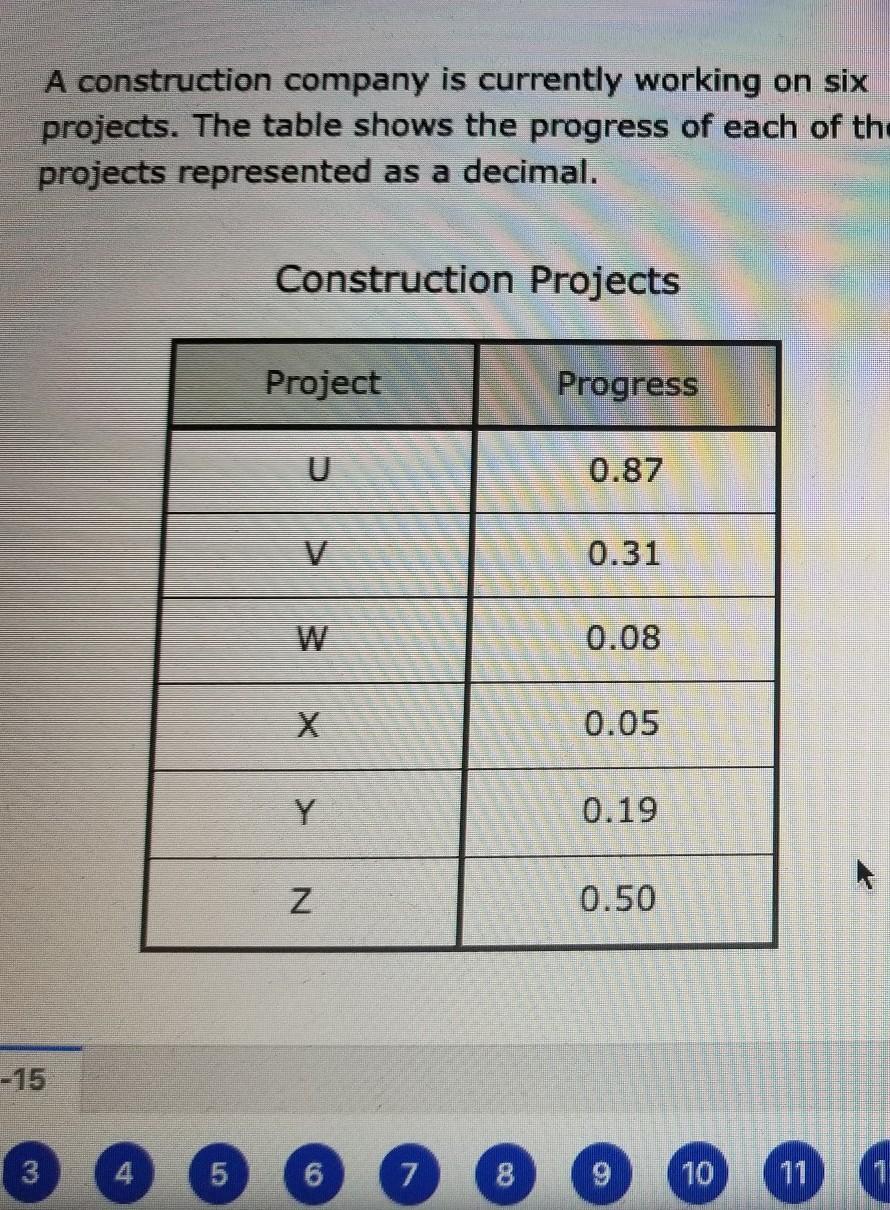
A construction company is currently working on six projects. The table shows the progress of each of the projects represented as a decimal.
What is the range of the progress of these projects?
Answers
Answer:
Step-by-step explanation:
can u give the answer to the quiz
The range of the project will be equal to 0.82.
What is the range in statistics?When the sample maximum and minimum are subtracted, the range of a set of data is the difference between the largest and smallest values. It uses the same units as the data to express itself.
The given data of the project is,
u 0.87
v 0.31
w 0.08
x 0.05
y 0.19
z 0.5
The range will be calculated as the difference between the maximum value to the minimum value.
Range = 0.84 - 0.05
Range = 0.82
Therefore, the range of the project will be equal to 0.82.
To know more about the range in statistics follow
https://brainly.com/question/8486248
#SPJ2
A can do a work in 14 days and working together A and B can do the same work in 10 days. In what time can B alone do the work? (i dont get this one, please explain :)
Answers
Answer:
35 days
Step-by-step explanation:
A = 14 days
It means per day, work done by A= 1 / 14
A+B = 10 days
Work done by A and B per day = 1 / 10
In what time can B alone do the work?
To solve this, we have
A+B = A alone + B alone
1/10 = 1/14 + B alone
Subtract 1/14 from both sides
1/10 - 1/14 = 1/14 + B alone - 1/14
14-10/140 = B alone
4/140 = B alone
B alone= 1 / 35
Work done of B alone = 1/35
B alone will do the work in 35 days
Answer:
35 days.
Step-by-step explanation:
A can do the work in 14 days: per day work done by A=1/14
A and B can do the work in 10 days: per day work done by A and B=1/10
Work is done by B per day=1/10–1/14=7/70-5/70=(7–5)/70=2/70=1/35.
So, B takes 35 days.
If Mary paid $21.87 for 8.1 pounds of strawberries, what was the price of 1
pound of strawberries? Do not include s in your answer
Answer here
Answers
Answer:
$2.70
Step-by-step explanation:
We know that $21.87 is for 8.1 pounds of strawberries.
To get the price of 1 pound, we divide $21.87 by 8.1.
That gives us $2.70.
If the measures of Arc RB=67.4 and the measures of Arc FU =38.1 what is m/_FWU? Picture isn’t drawn to scale, round your answer to the nearest hundredth
Answers
The measurement of angle FWU is given as follows:
< FWU = 14.65º.
How to obtain the measure of the arc?The measure is obtained using the two secant theorem, which states that the angle measure is half the difference between the angle measures of the two arcs.
The angle measures for each arc are given as follows:
Arc RB = 67.4.Arc FU = 38.1.The difference between these two measures is obtained as follows:
67.4 - 38.1 = 29.3.
The angle measure is half of this, hence it is obtained as follows:
< FWU = 0.5 x 29.3
< FWU = 14.65º.
More can be learned about the two secant theorem at https://brainly.com/question/26340897
#SPJ1
helpppppp ppppplease

Answers
9514 1404 393
Answer:
x = 6.99 fty = 5.66 ftStep-by-step explanation:
The mnemonic SOH CAH TOA can remind you of the relevant relationships. The given side is the hypotenuse. x is the side opposite the given angle.
Sin = Opposite/Hypotenuse
sin(51°) = x/(9 ft)
x = (9 ft)sin(51°)
x ≈ 6.99 ft
__
Cos = Adjacent/Hypotenuse
cos(51°) = y/(9 ft)
y = (9 ft)cos(51°)
y ≈ 5.66 ft
evaluate the line integral, where c is the given curve. (x 9y) dx x2 dy, Evaluate the line integral, where C is the given curve, Integral c (x+2y)dx+x^2dy, C consists of line segments from (0, 0) to (9, 1) and from (9, 1) to (10, 0)
Answers
the integral of the line, where c is the specified curve. The line integral is (x 9y) dx x2 dy, where C is the provided curve. The line segments from (0, 0) to (9, 1) and from (9, 1) to (10, 0), respectively, make up the integral c (x+2y)dx+x2dy, C. is 95/3
\(\int\limits^a_c {(x+9y,x^{2} )} \, dr_{2} = \int\limits^1_0{9+t+9-9t, (9+t )^2} .(1, -1)\, dt\)
it is possible to parameterize the first line segment by
\(r_{1} (t) = (0,0)(1-t) + (9,1)t = (9t,t)\) with 0 ≤ t ≤ 1 indicate this first section with \(C_{1}\) then
\(\int\limits^a_c {(x}+9y,x^2 ) \, dr_{1} = \int\limits^1_0 {(9t+9t,81t^2) . (9,1)} \, dt\\ \\= \int\limits^1_0 {(162t + 81t^2) } \, dt\\\\= 108\)
secondly the line segment \(C_{2}\) can be characterised as
\(r_{2} (t) = (9,1)(1-t) + (10,0)t = (9+t,1-t)\) again using interval 0 ≤ t ≤ 1 then
\(\int\limits^a_c {(x+9y,x^{2} )} \, dr_{2} = \int\limits^1_0{9+t+9-9t, (9+t )^2} .(1, -1)\, dt\)
= -229/3
finally ,
= 108-229/3
= 95/3
Learn more about interval here
https://brainly.com/question/18125359
#SPJ4
an experiment consists of tossing 4 unbiased coins simultaneously. the number of simple events in this experiment is question 20answer a. 10 b. 8 c. 16 d. 25
Answers
The number of simple events in this experiment is 16.
The correct answer to the given question is option c.
The probability of an event can be calculated by dividing the number of favorable outcomes by the number of possible outcomes. A simple event is one in which only one of the outcomes can occur. For example, if a coin is tossed, a simple event would be the outcome of the coin being heads or tails.
The total number of possible outcomes in the experiment of tossing 4 unbiased coins simultaneously is 2⁴, since there are two possible outcomes for each coin. Thus, the total number of possible outcomes is 16.
Each coin has two possible outcomes: heads or tails. If all four coins are flipped, there are two possible outcomes for the first coin, two possible outcomes for the second coin, two possible outcomes for the third coin, and two possible outcomes for the fourth coin. Therefore, the total number of possible outcomes is 2 × 2 × 2 × 2 = 16.
Therefore, the number of simple events in this experiment is 16, which is option (c).
For more such questions on simple events, click on:
https://brainly.com/question/10346457
#SPJ8
HURRY PLEASE I DONT WANT TO FAIL

Answers
Answer: 62
Step-by-step explanation: In the red empty spot, the #5 would go there and in the blue spot the #6 would go there. 8x2=16 and 16+16= 32: t=This is for the to rectangle shapes on both sides. Now for the square in the middle, since the red spot is 5 and the blue is 6, 5x6= 30. So, 30+32=62.
-2 times x to the second power
Answers

Find the total surface area of the prism.
13 in.
9 in.
15 in.
Need asap

Answers
Answer:
The surface area of a rectangular prism with length of
15, a width of 9 and a height of 13 is:
894.0000 square units.
not sure
Step-by-step explanation:
To find the surface area, use this rectangular prism surface area
formula:
Surface Area =
[(Length x Width) + (Length x Height) + (Width x Height)] x 2
Example: The surface area of a rectangular prism with length of
3 inches, width of 4 inches, and height of 5 inches:
Surface Area = [(3 x 4) + (3 x 5) + (4 x 5)] x 2
Calculated out this gives a surface area of 94 Square Inches.
(not the answer example)
wait plsss- i messed up.

Which of the following is an example of distributive property of multiplication over addition for rational numbers?
A
−14 × {23 + (−47)} = [−14 × 23] + [−14 × (−47)]
B
−14 × {23 + (−47)} = [14 × 23] − (−47)
C
−14 × {23 + (−47)} = 23 + (−14) × −47
D
−14 × {23 + (−47)} = {23 + (−47)} − 14
Answers
Your answer: A −14 × {23 + (−47)} = [−14 × 23] + [−14 × (−47)] This example demonstrates the distributive property of multiplication over addition for rational numbers, which states that for any rational numbers a, b, and c: a × (b + c) = (a × b) + (a × c).
The correct answer is A: −14 × {23 + (−47)} = [−14 × 23] + [−14 × (−47)]. This is an example of the distributive property of multiplication over addition for rational numbers because we are multiplying −14 by the sum of 23 and −47, and we can distribute the multiplication to each term inside the parentheses by multiplying −14 by 23 and −14 by −47 separately, and then add the two results together. This is the basic definition of the distributive property of multiplication over addition. Option B shows the distributive property of multiplication over subtraction, option C shows the product of multiplication and addition, and option D is not a valid equation.
Learn more about rational here:
https://brainly.com/question/20850120
#SPJ11
the ratio of dividends to the average number of common shares outstanding is:
Answers
The ratio of dividends to the average number of common shares outstanding is known as the dividend yield. It is a measure of the return on an investment in the form of dividends received relative to the number of shares held.
To calculate the dividend yield, you need to divide the annual dividends per share by the average number of common shares outstanding during a specific period. The annual dividends per share can be obtained by dividing the total dividends paid by the number of outstanding shares. The average number of common shares outstanding can be calculated by adding the beginning and ending shares outstanding and dividing by 2.
For example, let's say a company paid total dividends of $10,000 and had 1,000 common shares outstanding at the beginning of the year and 1,500 shares at the end. The average number of common shares outstanding would be (1,000 + 1,500) / 2 = 1,250. If the annual dividends per share is $2, the dividend yield would be $2 / 1,250 = 0.0016 or 0.16%.
In summary, the ratio of dividends to the average number of common shares outstanding is the dividend yield, which measures the return on an investment in terms of dividends received per share held.
To know more about dividend, here
brainly.com/question/3161471
#SPJ11
A lab assistant tracked an object’s travel time in hours. However, the lab director wants the time tracked in minutes.
A 2-column table with 4 rows. Column 1 is labeled hours with entries 0.5, 0.75, 1.5, 2.5. Column 2 is labeled Minutes with entries 30, 45, 90, blank.
Help the lab assistant complete the table. How many minutes did the object travel after 2.5 hours?
Answers
Answer:
150
Step-by-step explanation:
Answer: 150!
Step-by-step explanation:
i did the edge test, i got it right. trust me, i dont lie. :) have a nice day<3
proof:

Parallel and transversals

Answers
I was in a rush so I couldn't write fown the steps. If you need the explanations for how they were gotten, please say.

It is Marcie's first turn to roll. Which ratio shows the theoretical probability that she will not land on a star space? 1/6 1/3 1/2 2/3
Answers
Answer:
\(P(Not\ Star) =\frac{2}{3}\)
Step-by-step explanation:
Given
See attachment
Required
Theoretical probability that a roll will not land on a star
From the attachment, we have:
\(n = 12\) --- Total space
\(Star = 4\)
So, the theoretical probability that a roll will land on a star is:
\(P(Star) = \frac{n(Star)}{n}\)
\(P(Star) = \frac{4}{12}\)
\(P(Star) = \frac{1}{3}\)
Using the complement rule, the probability that it will not land on a star is:
\(P(Not\ Star) = 1 - P(Star)\)
\(P(Not\ Star) = 1 - \frac{1}{3}\)
Take LCM
\(P(Not\ Star) =\frac{3-1}{3}\)
\(P(Not\ Star) =\frac{2}{3}\)

Answer:
Look at the photo below
Step-by-step explanation:

If the RADIUS of a circle is 9 meters, then the DIAMETER is? *
25 points
4.5 meters
12 meters
18 meters
27 meters
Answers
What letter represents the y-intercept?
x
b
m
Answers
Answer:
The letter that represents the y-intercept is B!
Step-by-step explanation:
It indicates point of intersection between the y-axis and the line.
Hope this helps you alot! Also can you give me a Brainliest?
PLEASE!!!
The radius of a circle is increasing at a rate of 8 centimeters per minute. Find the rate of change of the area when the radius is 2 centimeters. Round your answer to one decimal place.
Answers
The rate of change of the area when the radius is 2 centimeters is approximately 100.5 square centimeters per minute.
To find the rate of change of the area of a circle when the radius is 2 centimeters, we need to use the formula for the area of a circle, which is \(A = πr^2.\)
We know that the radius is increasing at a rate of 8 centimeters per minute, so we can use this information to find the rate of change of the area.
We can start by finding the area of the circle when the radius is 2 centimeters. Substituting r = 2 into the formula, we get:
A = π(2)^2
A = 4π
So the area of the circle is 4π square centimeters when the radius is 2 centimeters.
Now, let's find the derivative of the area with respect to time. Using the power rule of differentiation, we get:
dA/dt = 2πr (dr/dt)
Substituting r = 2 and dr/dt = 8, we get:
dA/dt = 2π(2)(8)
dA/dt = 32π
So the rate of change of the area when the radius is 2 centimeters is 32π square centimeters per minute. To round this to one decimal place, we can use a calculator to get:
dA/dt ≈ 100.5
Therefore, the rate of change of the area when the radius is 2 centimeters is approximately 100.5 square centimeters per minute.
Learn more about centimeters here:
https://brainly.com/question/19098836
#SPJ11
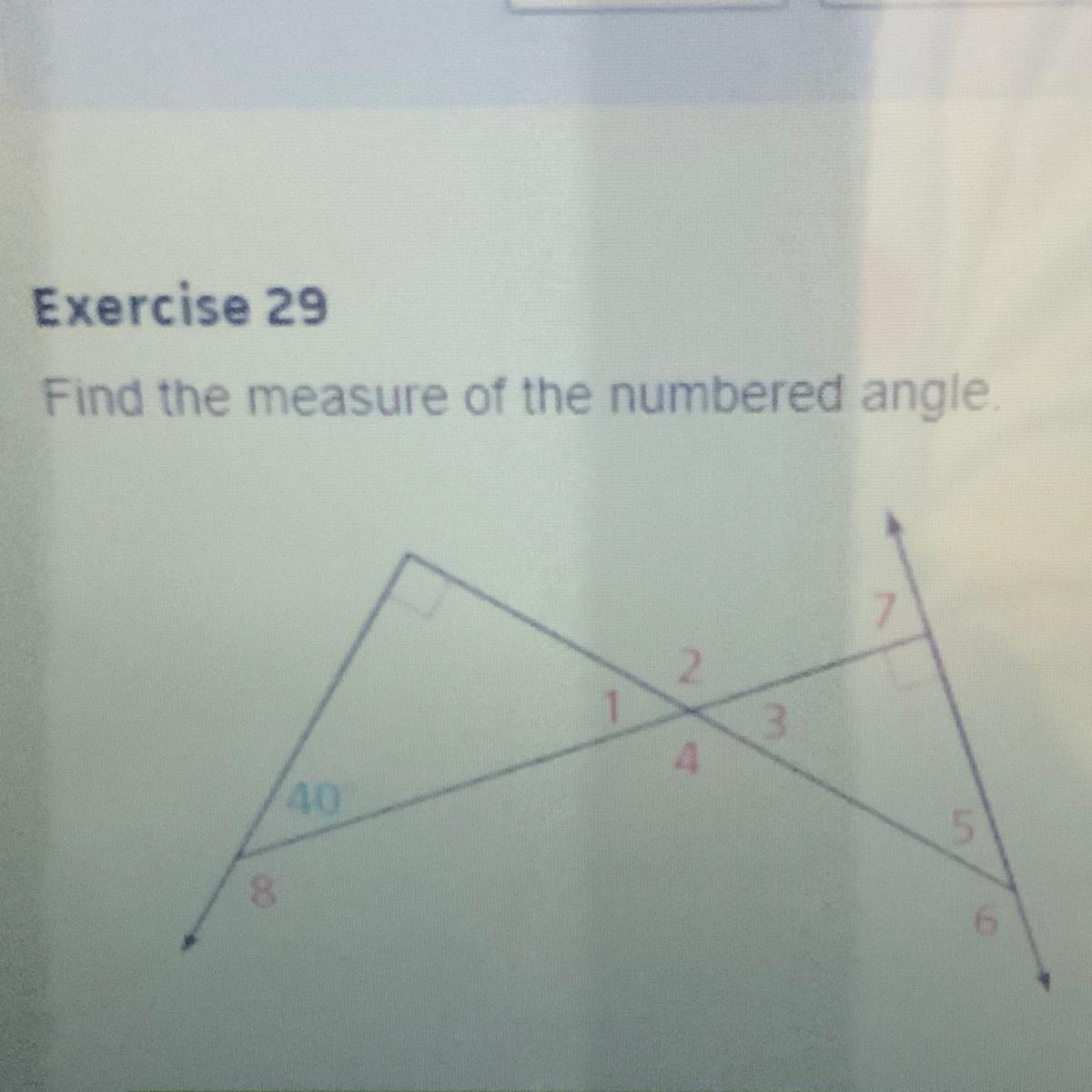
Find the measure of the numbered angle
Answers
angle 2: 130
angle 3: 50
angle 4: 130
angle 5: 40
angle 6: 140
angle 7: 90
angle 8: 140
Answer:
1 = 50°, 2 = 130°, 3 = 50°, 4 = 130°, 5 = 40°, 6 = 140°, 7 = 90°, 8 = 140°
Step-by-step explanation:
The sum of the angles of a triangle is 180°. A flat angle measures 180° as well.
Angle 1: 180 - 90 - 40 = 50°
Angle 2: 180 - 50 = 130°
Angle 3: 180 - 130 = 50°
Angle 4: 180 - 50 = 130°
Angle 5: 180 - 90 - 50 = 40°
Angle 6: 180 - 40 = 140°
Angle 7: 180 - 90 = 90°
Angle 8: 180 - 40 = 140°
It's a little complicated, but I hope this helps!
A line is drawn over this rectangle.
Is the line a line of symmetry?


Answers
Based on the definition of a line of symmetry, we can conclude that: "the line is not a line of symmetry, because the two parts are not an exact match when the rectangle is folded over the line."
What is a Line of Symmetry?A line of symmetry is like a mirror that splits a shape into two parts that look exactly the same. If you fold a shape in half along a line and both sides look exactly the same, that line is called a line of symmetry.
Thus, from the image shown with the rectangle given, we can conclude that: "the line is not a line of symmetry, because the two parts are not an exact match when the rectangle is folded over the line."
Learn more about Line of Symmetry on:
https://brainly.com/question/14231935
#SPJ1
3) Assume the function f computes the number y in millions of people using the internet in year x. f = {(1996, 1.2), (1998, 4.3), (2000, 9.8) Evaluate f(2000) and give the domain and range of f A) f(2000) = 1.2; D: (1996, 1998, 2000), R: (1.2, 4.3, 9.8) B) f(2000) = 9.8; D: (1996, 1998, 2000), R: {1.2, 4.3, 9.8} C) f(2000) = 4.3; D: (1.2, 4.3, 9.8), R: (1996, 1998, 2000} D) f(2000) = 9.8; D: (1.2, 4.3, 9.8), R: (1996, 1998, 2000) Solve the problem. 17) Suppose A dollars is deposited in a savings account paying 7.5% interest compounded 0 continuously. After x years the account will contain A(x) = A 20.075x dollars. If $520 is initially deposited in this account, how much would be in the account after 8 years? Round to the nearest cent. A) $1359.54 B) $560.50 C) $947.50 D) $1.82
Answers
The correct answer is A) $1359.54. To evaluate f(2000), we need to find the corresponding y-value in the given function f at x = 2000.
From the given data, we have f = {(1996, 1.2), (1998, 4.3), (2000, 9.8)}. Looking at the function f, we see that f(2000) = 9.8.
The domain of f is the set of x-values for which we have corresponding y-values. In this case, the domain is D: {1996, 1998, 2000}.
The range of f is the set of y-values obtained from the function. In this case, the range is R: {1.2, 4.3, 9.8}.
Therefore, the correct answer is B) f(2000) = 9.8; D: {1996, 1998, 2000}, R: {1.2, 4.3, 9.8}.
For the second part of the question:
We are given the formula for the account balance after x years as A(x) = A * 20.075^x, where A represents the initial deposit.
In this case, the initial deposit A is $520. We need to find the account balance after 8 years, so we substitute x = 8 into the formula.
A(8) = 520 * 20.075^8
Using a calculator, we can compute this value to be approximately $1359.54.
To learn more about function click here:
brainly.com/question/30721594
#SPJ11
Write the square or cube fit each number.

Answers
Answer and Step-by-step explanation:
1) 12*12 = 144
2) 2*2*2 = 8
A pizza parlor charges $8 per pizza plus $0.65 per topping. Which equation can be used to find the cost of a pizza that costs $11.25?
Group of answer choices
8x+0.65=11.25
8+0.65x=11.25
8-0.65x=11.25
8x-0.65=11.25
Answers
(x,-4) and (2,8) m= -3
Answers
Answer:
x=6
Step-by-step explanation:
we know that
slope formula is,
m=(y2-y1) / (x2-x1)
where m=-3
x1=x,y1=-4 and x2=2,y2=8,
-3=(8-(-4))/(2-x)
Now solving the expression
we get,
-6+3x=12
3x=18
x=6
Two right angles are similar if the acute angles of one triangle are congruent to the acute angles of the other triangle A true B false
Answers
its true
they are both already right triangles so if both have acute angles that are congruent then the right triangles are similar
if one of the acute angles of a right triangle is congruent to an acute angle of another right triangle then by angle angle Similarity the triangles are similar
The total price for a computer and a
printer was $1039. If the computer
cost $750, how much did the printer
cost?
Answers
Answer:
$289
Step-by-step explanation:
If you know the cost of one of the two items, you can subtract that item from the total in order to find the price of the second item
So: total price - computer price = printer cost
So: $1039- $750 = $289
The printer is $289
ANSWER PLEASE HURRY!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer
put 1 on top and exo on bottom
Step-by-step explanation:
What is the y-intercept of the function ?

Answers
Answer:
The y-intercept answer will be 2/9