There are 10 brown, 10 black, 10 green, and 10 gold marbles in bag. A student pulled a marble, recorded the color, and placed the marble back in the bag. The table below lists the frequency of each color pulled during the experiment after 40 trials.
Outcome Frequency
Brown 13
Black 9
Green 7
Gold 11
Compare the theoretical probability and experimental probability of pulling a gold marble from the bag.
The theoretical probability, P(gold), is 25%, and the experimental probability is 27.5%.
The theoretical probability, P(gold), is 50%, and the experimental probability is 11.5%.
The theoretical probability, P(gold), is 25%, and the experimental probability is 25%.
The theoretical probability, P(gold), is 50%, and the experimental probability is 13.0%.
Answers
The theoretical probability, P(brown), is 25%, and the experimental probability is 32.5%.
In this question, we have been given there are 10 brown, 10 black, 10 green, and 10 gold marbles in bag.
The theoretical probability of pulling a brown marble from the bag would be,
P = 10/40
P = 0.25
P = 25%
A student pulled a marble, recorded the color, and placed the marble back in the bag.
The frequency of each color pulled during the experiment after 40 trials is:
Brown 13
Black 9
Green 7
Gold 11
So, the experimental probability of pulling a brown marble from the bag would be,
P = 13/40
P = 0.325
P = 32.5 %
Therefore, the theoretical probability, P(brown), is 25%, and the experimental probability is 32.5%.
Learn more about the probability here:
brainly.com/question/3679442
#SPJ1
Related Questions
an agency for the us government spends millions of dollars funding research on cancer. in particular, 20 research projects are funded to test a drug used to reduce pancreatic tumors. in one of these projects (project number 11) researchers find that the drug significantly reduces the size of tumors with a p-value of 0.027. there are no significant effects found in the other 19 projects (p-values all greater than 0.05) for the drug. given the entirety of this information, would it be proper to conclude that the drug is effective in reducing the size of pancreatic tumors?
Answers
The result from project number 11 suggests that the drug may be effective in reducing the size of pancreatic tumors, but it is not sufficient to conclude definitively that the drug is effective using hypothesis.
The p-value of 0.027 indicates that if there were truly no effect of the drug, the probability of observing a result as extreme as or more extreme than what was observed in project number 11 would be 0.027. This suggests that the result is unlikely to have occurred by chance alone. However, it is possible that the result is a false positive or due to chance variation, especially given that 20 research projects were conducted. It would be important to replicate the result in additional studies and consider the overall body of evidence before concluding definitively that the drug is effective.
To know more about hypothesis,
https://brainly.com/question/31592172
#SPJ11
The polynomial equation x^3−x^2+kx−3=0
has three roots that are all integers.
Find the value of integer k
Answers
The value of integer k is -5.
What is polynomial equations ?
Polynomial equations formed with variables, exponents and coefficients .
Since the polynomial has three integer roots, we can express it as:
(x - r1)(x - r2)(x - r3) = 0
where r1, r2, and r3 are the three integer roots.
Expanding the left-hand side, we get:
x^3 - (r1 + r2 + r3)x^2 + (r1r2 + r1r3 + r2r3)x - r1r2r3 = 0
Comparing this with the given polynomial, we see that:
r1 + r2 + r3 = 1
r1r2 + r1r3 + r2r3 = k
r1r2r3 = 3
First we need to find the value of k. From the first equation, we see that one of the roots must be 1, since the sum of three integers that are not 1 cannot be 1. Without loss of generality, assume that r1 = 1. Then we have:
r2 + r3 = 0
r2r3 = 3
Since the roots are integers, the only possibility is r2 = -3 and r3 = 1.
Therefore, we have:
k = r1r2 + r1r3 + r2r3 = 1(-3) + 1(1) + (-3)(1) = -5
Therefore, the value of integer k is -5.
Learn more about polynomial equation here :brainly.com/question/28947270
#SPJ1
100 POINTS!!! PLEASE HELP ME


Answers
Step-by-step explanation:
For question 30, the first choice is not necessarily true. I attached a picture of what *could* be the parallelogram.
The first choice is true ONLY if the parallelogram is a square.
The second choice is not necessarily true either. It is true ONLY if the parallelogram is a rhombus (a square is also a rhombus, just for reference)
But opposite sides of a parallelogram are always equal
So the answer to question 30 are the first and second choices.
For question 31:
remember what I said about how opposite sides of a parallelogram are always equal? Well opposite angles are also always equal.
So angle BKX = angle BWX = angle XWB = 114 degrees
Angle BKW = angle XWK (using parallel lines) = angle XWB - angle BWK = 114 - 22 = 92 degrees
Angle WBX = angle BXK (using parallel lines too) = angle WXK - angle WXB.
Consecutive angles in a parallelogram add up to 180. So angle WXK + angle XWK = 180. angle WXK = 180 - angle XWK = 180 - 114 = 66 degrees.
angle WDB + angle WBX + angle BWK = 180 because it's a triangle
angle WDB + 66 (just figured it out) + 22 (given) = 180 degrees
angle WDB = 180 - 66 - 22 = 92 degrees
I hope I didn't do anything wrong lol
but I prolly did XD
Answer:
angle WDB + angle WBX + angle BWK = 180 because it's a triangle
angle WDB + 66 + 22 (given) = 180 degrees
angle WDB = 180 - 66 - 22 = 92 degrees
Step-by-step explanation:
(1 point) use spherical coordinates to evaluate the triple integral∭E e^−(x2 + y2 + z2)/ √x2 +y2+ z2 dV,where E is the region bounded by the spheres x2+ y2+ z2=1 and x2+ y2+ z2=16. ANSWER = _____
Answers
When E is the region bounded by the spheres then the answer to the triple integral is -π/2 (e⁻¹ - e⁻¹⁶)
To evaluate the triple integral using spherical coordinates, we need to express the volume element dV in terms of spherical coordinates and determine the limits of integration.
In spherical coordinates, the volume element dV is given by:
dV = ρ² sin(φ) dρ dφ dθ
where ρ represents the radial distance, φ represents the polar angle (measured from the positive z-axis), and θ represents the azimuthal angle (measured from the positive x-axis in the xy-plane).
The given region E is bounded by the spheres x² + y² + z² = 1 and x² + y² + z² = 16. These can be expressed in terms of ρ as:
1 ≤ ρ ≤ 4
To determine the limits of integration for φ and θ, we consider the spherical symmetry of the problem. Since the region is bounded by spheres, the limits for both φ and θ will be the full range of [0, π] and [0, 2π], respectively.
Now, let's evaluate the triple integral:
∭E e(-x² - y² - z²) / √(x² + y² + z²) dV
= ∫₀²π ∫₀ᴨ ∫₁⁴ e(-ρ²) / ρ ρ² sin(φ) dρ dφ dθ
= ∫₀²π ∫₀ᴨ ∫₁⁴ e(-ρ²) ρ sin(φ) dρ dφ dθ
Since the integrand does not depend on θ, we can simplify the triple integral:
= ∫₀²π ∫₀ᴨ [-e(-ρ²) cos(φ)]₁⁴ sin(φ) dφ dθ
= ∫₀²π [-e(-ρ²) cos(φ) sin(φ)]₁⁴ dθ
= ∫₀²π [-e(-ρ²) / 4] dθ
= -e(-ρ²) / 4 [θ]₀²π
= -e(-ρ²) / 4 (2π - 0)
= -π/2 (e(-ρ²))
Now, we need to evaluate this expression within the limits of ρ:
= -π/2 ∫₁⁴ e(-ρ²) dρ
To solve this integral, we can use the substitution u = -ρ², which gives du = -2ρ dρ. The limits of integration transform accordingly:
u = -1, u = -16
∫ eu du = eu [u]_{-1}{-16} = e⁻¹ - e⁻¹⁶
Please note that the above expression represents the numerical value of the triple integral.
You can learn more about triple integral at: brainly.com/question/2289273
#SPJ11
Is there enough info to prove that TU || QR ?

Answers
The line TU is parallel to QR and SQR is dilated version of STU by a scale factor of 4.
What is midpoint theorem?
The line segment of a triangle connecting the midpoint of two sides of the triangle is said to be parallel to its third side and is also half the length of the third side, according to the midpoint theorem.
Through the diagram it can be seen that T and U are midpoints of SQ and SR respectively.
And it can also be seen that TU is parallel to QR.
It is given that ST = 2, TQ = 6, SU = 3 and UR = 9
The length of side SQ -
SQ = ST + TQ
SQ = 2+6
SQ = 8
The length of side SR -
SR = SU + UR
SR = 3+9
SR = 12
The measurement of QR = SQ as seen in the diagram.
According to midpoint theorem the mid points line segment TU measures half of its parallel third side of triangle QR.
Now, to find the scale factor -
= QR - TU
= 8 - 4
= 4
Therefore, the scale factor is 2.
To learn more about midpoint theorem from the given link
https://brainly.com/question/28667736
#SPJ1
if a rep works eight hours per day and the average length of a call is 30 minutes and the average travel time is 30 minutes and the rep works 250 days per year, then what is the total annual number of calls the rep can make?
Answers
Applying basic unitary method and time conversion, The answer is 3750 calls annually.
What is Unitary method?The unitary approach involves calculating the value of a single unit, from which we can calculate the values of the necessary number of units.
Why do we use unitary method?The unitary technique is used practically all the time, from problems involving speed, distance, and time to issues with estimating material costs. The technique is applied to determining a product's pricing. It is used to determine how long it takes a person or vehicle to travel a certain distance in an hour.
average length of call= 30 minutes
average travel time=30 minutes
annual working days=250
per day works 8 hours.
call hour in work = 8*60 - 30 = 450minutes.
number of calls made in those hours= 450/30=15 calls daily.
total annual number of calls= 250 * 15 = 3750
To learn more about unitary method visit:
https://brainly.com/question/28276953
#SPJ4
Need help to solve it in standard form ( y= mx+b )
4x+9y= -63
2x-3y= -9
Answers
Answer:
Answers below
Step-by-step explanation:
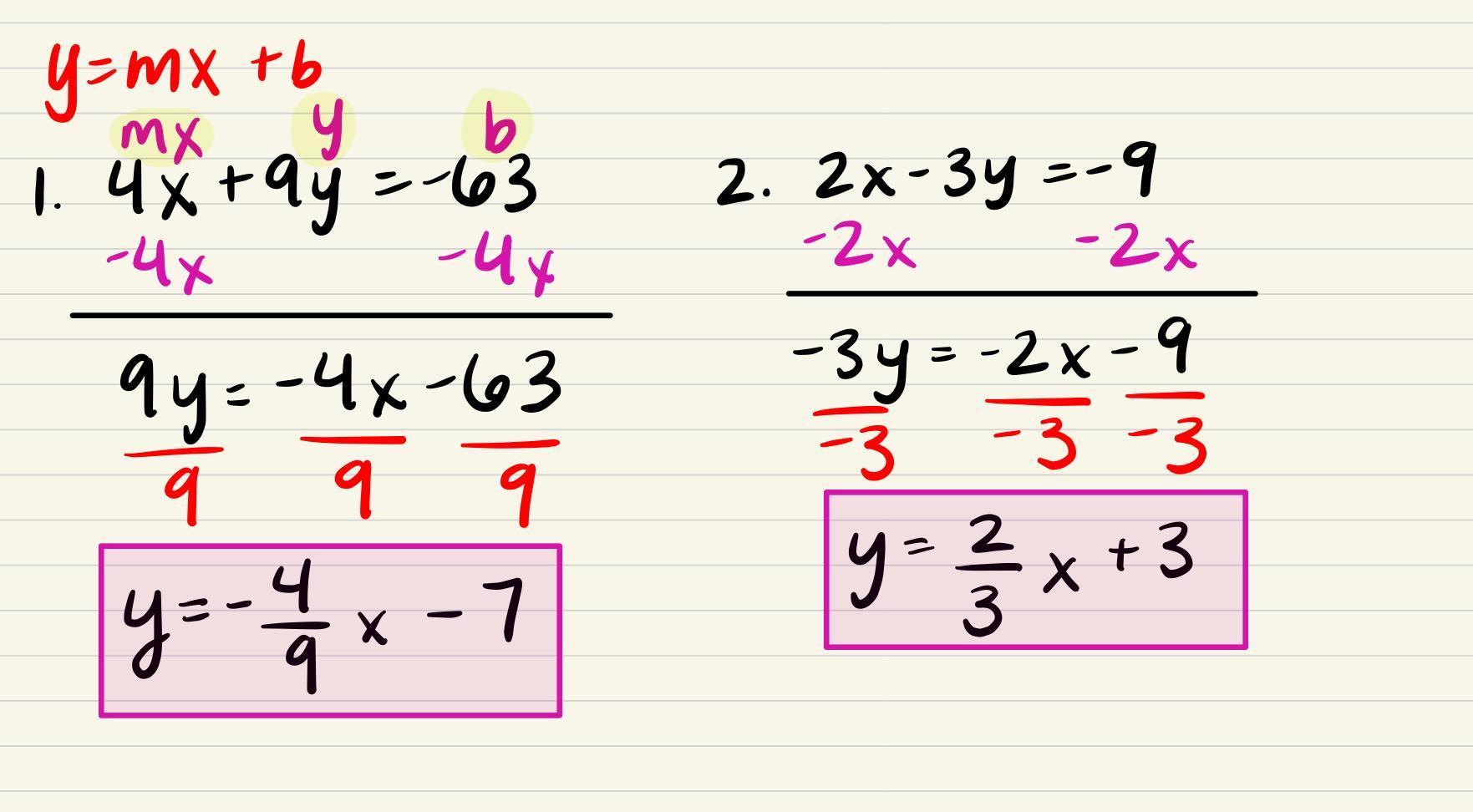
show all the nesessary steps
i will make brainlist answer

Answers
Answer:
hey there you go with the steps , please mark as brainliest

Use the data table below to create the given scatter plot, then fill in the guided sentence below. I just need the sentence.

Answers
Using visual interpretation of the plot trend, the scatter plot shows positive correlation.
A positive correlation is depicted by a positive slope or trend line on a scatter plot. The trend of the scatter plot slopes upward which establishes a positive association.
If the slope is otherwise negative, such that the trend line slopes downward, then we have a negative association or relationship.
Therefore, the scatter plot shows positive relationship.
Learn more on scatter plot:https://brainly.com/question/6592115
#SPJ1
Find the measure of

Answers
Answer:
50 degrees
Step-by-step explanation:
Line CDF is 180 degrees
76 and 54 and some part of the 180 degrees
1. add 76+54 = 130
2. subtract 180-130 = 50
Mrs. Johnson put 22,250 miles
on her car in 2011 and 14,500
miles in 2012. Find the percent
decrease in miles driven
from 2011 to 2012.
help.
Answers
The change in quantities can be represented as percentage
The percentage decrease in miles driven is 34.83%
The given parameters are:
\(\mathbf{Initial = 22250}\)
\(\mathbf{Final = 14500}\)
The percentage decrease is calculated as:
\(\mathbf{\%Decrease = \frac{Final - Initial}{Initial} \times 100\%}\)
Substitute known values
\(\mathbf{\%Decrease = \frac{14500- 22250}{22250} \times 100\%}\)
\(\mathbf{\%Decrease = \frac{-7750}{22250} \times 100\%}\)
\(\mathbf{\%Decrease = \frac{-775000}{22250} \%}\)
\(\mathbf{\%Decrease = -34.83 \%}\)
The negative sign implies that, the change represents a decrement.
Hence, the percentage decrease in miles driven is 34.83%
Read more about percentage change at:
https://brainly.com/question/14801224
Mr. ross needed a box for his tools. he knew that the box had to be between 100 cubic inches and 150 cubic inches. which dimension shows the tool he can use
Answers
Mr. Ross can choose any dimensions for the length, width, and height as long as their product falls within the given volume range of 4 * 5 * 5 to 6 * 5 * 5 cubic inches.
To help you find the dimensions for Mr. Ross's tool box that can hold between 100 and 150 cubic inches, let's consider the following terms: volume, length, width, and height.
1. Volume: The space occupied by the tool box, which should be between 100 and 150 cubic inches.
2. Length, Width, and Height: The dimensions of the tool box that will determine its volume.
To find the dimensions for the tool box that meets Mr. Ross's requirements, we can use the formula for volume of a rectangular box:
Volume = Length × Width × Height
We need to find the Length, Width, and Height such that 100 ≤ Volume ≤ 150.
Unfortunately, without more specific information about the dimensions Mr. Ross prefers or the shape of the box, we cannot provide an exact set of dimensions. However, he can choose any dimensions for the length, width, and height as long as their product falls within the given volume range of 100 to 150 cubic inches.
To know more about dimensions refer here:
https://brainly.com/question/28688567
#SPJ11
A company manufactures three types of cabinets, type A, type B, and type C. Last week, the number of type B cabinets produced was 30 more than 1/2 the number of type A cabinets produced. If the company made the same number of type B and type C cabinets last week, then the number of type A cabinets produced was _ the total number of cabinets produced last week was _
Answers
Answer:
Type A cabinets generated was 10
Type B and type C cabinets generated were 35
So, the total cabinets produced is 45
Step-by-step explanation:
It is given that
B = 1 ÷ 2 A + 30
C = 3 ÷ 2A + 20
Now equate these
B = C
1 ÷ 2A + 30 = 3 ÷ 2A + 20
30 - 20 = 3 ÷ 2A - 1 ÷ 2A
10 = A
Now put the A value in any of the above equation
B = 1 ÷ 2A + 30
B = 1 ÷ 2(10) + 30
B = 5 + 30
B = 35
And,
C = 3 ÷ 2A + 20
C = 3 ÷ 2(10) + 20
C = 15 + 20
C = 35
Therefore
Type A cabinets generated was 10
Type B and type C cabinets generated were 35
the total cabinets produced is 45
Write the equation of the line in point-slope form that has slope 3 and passes through (2 ,-5)
Answers
Answer:
\(\huge\boxed{y+5=3(x-2)}\)
Step-by-step explanation:
The point-slope form of an equation of a line:
\(y-y_1=m(x-x_1)\)
We have
\(m=3;\ (2;\ -5)\to x_1=2;\ y_1=-5\)
Substitute:
\(y-(-5)=3(x-2)\\\\y+5=3(x-2)\)
The equation of the line in a point-slope form that has slope 3 and passes through (2,-5) is y = 3x - 11
What is the Point-slope form?The equation of the straight line has its slope and given point.
If we have a non-vertical line that passes through any point(x1, y1) and has a gradient m. then general point (x, y) must satisfy the equation
y-y₁ = m(x-x₁)
Which is the required equation of a line in a point-slope form.
Given that line in a point-slope form that has slope 3 and passes through (2,-5)
Therefore, m = 3
Now substituting;
y-y₁ = m(x-x₁)
y- -5 = 3(x- 2)
y = 3x - 6 - 5
y = 3x - 11
Hence, the equation of the line in a point-slope form that has slope 3 and passes through (2,-5) is y = 3x - 11
Learn more about slope here:
https://brainly.com/question/2503591
#SPJ2
find the perimeter of the window to the nearest hundredth

Answers
The perimeter of the window to the nearest hundredth will be;
⇒ 102.8 cm
What is Circle?
The circle is a closed two dimensional figure , in which the set of all points is equidistance from the center.
Given that;
The shape of window is semicircle.
And, The radius of window (r) = 20 cm
Now,
We know that;
The perimeter of semicircle = πr + 2r
Here, The radius of window (r) = 20 cm
So, We get;
The perimeter of the window = πr + 2r
= 3.14 x 20 + 2 x 20
= 62.8 + 40
= 102.8 cm
Thus, The perimeter of the window to the nearest hundredth will be;
⇒ 102.8 cm
Learn more about the circle visit:
https://brainly.com/question/24810873
#SPJ1
determine whether the property is true for all integers, true for no integers, or true for some integers and false for other integers. justify your answers. the average of any two odd integers is odd.
Answers
The property of the average of any two odd integers being odd is true for all integers.
This is because the sum of any two odd integers is always an even integer. For example, if we take any two odd integers, say 3 and 7, then the sum of these two is 10, an even integer. Therefore, the average of 3 and 7, which is (3 + 7)/2, is also an even integer, in this case, 5.
Since all even integers are divisible by 2, the average of any two odd integers must be an odd integer.
Therefore, the property is true for all integers.
To know more about integers refer here:
https://brainly.com/question/15276410#
#SPJ11
Marcus has a life insurance policy that will pay his family $35,000 per year if he dies. If interest rates are at 2.5% when the insurance company has to pay, what is the amount of the lump sum that the insurance company must put into a bank account ?
A. $350,000
B. $3.5 million
C. $1.4 million
D. $1 million
Answers
Answer:
$1.4 million
Step-by-step explanation:
A P E X
Answer:1.4 million
Step-by-step explanation:
Question 8 (1 point)
Explain what you did to arrive at that answer. If
you used an equation, be sure to explain why you
used each number in your math equation
Question eight goes with question seven

Answers
Using an exponential equation, it is found that 4 mg of the substance would still be left after 32 days.
What is an exponential function?The equation for the amount of the substance y after x half-lifes is given by:
\(y = a(0.5)^x\)
In this problem, the initial mass is of a = 64 mg.
Considering a half-life of 8 days, 32 days is equivalent to x = 32/8 = 4 half-lifes, hence:
\(y = 64(0.5)^4 = 4\)
4 mg of the substance would still be left after 32 days.
More can be learned about exponential equations at https://brainly.com/question/25537936
The medians of TUV are TX, UY, and VW. They meet at a single point Z.
(In other words, Z is the centroid of TUV.)
Suppose UZ=8, VW=33, and ZX=5.
Find the following lengths.
Note that the figure is not drawn to scale.

Answers
Answer:
TZ = 10 units
UY = 12 units
ZW = 11 units
Step-by-step explanation:
Point Z is the centroid of ΔTUV.
Since, centroid of a triangle is located on each median so that it divides each median in the ratio of 2 : 1
Therefore, TZ = 2(ZX)
TZ = 2(5) = 10 units
UY = UZ + ZY
= UZ + \(\frac{1}{2}(UZ)\)
= \(\frac{3}{2}UZ\)
= \(\frac{3}{2}\times 8\)
= 12 units
ZW = \(\frac{1}{3}(VW)\)
= \(\frac{1}{3}(33)\)
= 11 units
Triangle ABC is shown in the xy-coordinate plane. The triangle will be translated 2 units down and 3 units right to create triangle A'B'C'. Indicate whether each of the listed parts of the image will or will not be the same as the corresponding part in the preimage (triangle ABC) by selecting the appropriate box in the table.

Answers
The coordinates of A' and C' will not be the same. The perimeter and area of ΔA'B'C' will be the same. The measure of ∠B' and the slope of A'C' will be the same.
What is the transformation of a graph?Transformation is rearranging a graph by a given rule it could be either increment of coordinate or decrement or reflection.
If we reflect any graph about y = x then the coordinate will interchange it that (x,y) → (y,x).
As per the given translation,
2 units down and 3 units right
The coordinate will change as,(x,y) → (x+3,y-2) so it will change.
The transformation consists only of linear transformation no rotation exists thus area and perimeter will remain the same.
The slope and angle are unchanged irrespective of any transformation.
Hence "A' and C' will not have the same coordinates. The boundaries and surface area of ΔA'B'C' will be identical. The slope of A'C' and the measure of ∠B will be equal.".
To learn more about the transformation of graphs,
brainly.com/question/3099136
#SPJ1
Simplify the expression (7 + 5) + 4 • 13 – 2.
please show your work step by step explanations please and thank you.
Answers
The solution to the expression (7 + 5) + 4 • 13 – 2 is 62
How to simplify the expression?The expression is given as:
(7 + 5) + 4 • 13 – 2
Evaluate the expression in bracket
(7 + 5) + 4 • 13 – 2 = (12) + 4 • 13 – 2
Remove the bracket in the expression
(7 + 5) + 4 • 13 – 2 = 12 + 4 • 13 – 2
Evaluate the product in the expression
(7 + 5) + 4 • 13 – 2 = 12 + 52 – 2
Evaluate the sum in the expression
(7 + 5) + 4 • 13 – 2 = 64– 2
Evaluate the difference in the expression
(7 + 5) + 4 • 13 – 2 = 62
Hence, the solution to the expression (7 + 5) + 4 • 13 – 2 is 62
Read more about expressions at:
https://brainly.com/question/723406
#SPJ1
How to prove the vertical Angles Theorem
Answers
Answer:
see below
Step-by-step explanation:
Angles opposite each other when two lines cross. (see attached)
in the attached example, the angle a° and b° are vertical angles.

Step-by-step explanation:
\(
\underline{\bf{Given\::}}
Given:
\underline{\bf{To\:find\::}}
Tofind:
\underline{\bf{Explanation\::}}
Explanation:
\boxed{\bf{\frac{1}{f} =\frac{1}{v} -\frac{1}{u} }}}}
\begin{gathered}\longrightarrow\sf{\dfrac{1}{-10} =\dfrac{1}{v} -\dfrac{1}{-30} }\\\\\\\longrightarrow\sf{\dfrac{1}{v} =\dfrac{1}{-10} +\dfrac{1}{30} }\\\\\\\longrightarrow\sf{\dfrac{1}{v} =\dfrac{-3+1}{30} }\\\\\\\longrightarrow\sf{\dfrac{1}{v} =\cancel{\dfrac{-2}{30} }}\\\\\\\longrightarrow\sf{\dfrac{1}{v} =\dfrac{1}{-15} }\\\\\\\longrightarrow\sf{v=-15\:cm}\end{gathered}
⟶
−10
1
=
v
1
−
−30
1
⟶
v
1
=
−10
1
+
30
1
⟶
v
1
=
30
−3+1
⟶
v
1
=
30
−2
⟶
v
1
=
−15
1
⟶v=−15cm
\boxed{\bf{M \:A \:G \:N\: I \:F \:I \:C\: A\: T \:I \:O\: N :}}
MAGNIFICATION:
\begin{gathered}\mapsto\sf{m=\dfrac{Height\:of\:image\:(I)}{Height\:of\:object\:(O)} =\dfrac{Distance\:of\:image}{Distance\:of\:object} =\dfrac{v}{u} }\\\\\\\mapsto\sf{m=\cancel{\dfrac{-30}{-15}} }\\\\\\\mapsto\bf{m=2\:cm}\end{gathered}
↦m=
Heightofobject(O)
Heightofimage(I)
=
Distanceofobject
Distanceofimage
=
u
v
↦m=
−15
−30
↦m=2cm
Thus;
The magnification will be 2 cm .
\)
Sorry it’s kinda blurry

Answers
explanation: im just right
asking whether the linear system corresponding to an augmented matrix [a1 a2 a3 b] has a solution amounts to asking whether b is in span {a1, a2, a3}.
Answers
To determine if the linear system corresponding to an augmented matrix [a1 a2 a3 b] has a solution, we can check whether the vector b is in the span of the vectors {a1, a2, a3}.
In linear algebra, the augmented matrix represents a system of linear equations. The columns a1, a2, and a3 correspond to the coefficients of the variables in the system, while the column b represents the constants on the right-hand side of the equations. To check if the system has a solution, we need to determine if the vector b is a linear combination of the vectors a1, a2, and a3.
If the vector b lies in the span of the vectors {a1, a2, a3}, it means that b can be expressed as a linear combination of a1, a2, and a3. In other words, there exist scalars (coefficients) that can be multiplied with a1, a2, and a3 to obtain the vector b. This indicates that there is a solution to the linear system.
On the other hand, if b is not in the span of {a1, a2, a3}, it implies that there is no linear combination of a1, a2, and a3 that can yield the vector b. In this case, the linear system does not have a solution.
Therefore, determining whether the vector b is in the span of {a1, a2, a3} allows us to determine if the linear system corresponding to the augmented matrix [a1 a2 a3 b] has a solution or not.
Learn more about matrix here:
https://brainly.com/question/29132693
#SPJ11
Carl used 24 blocks to build a tower. Each block is a cube with side length of 2 inches. Use the formula v = s3 to find the volume of a cube. What is the volume of the tower?
Answers
Answer:
184
Step-by-step explanation:
What is 1 + 1
A. 1
B. 2
C. 10,000,000
D. 5
Answers
Answer:
E. - 11
Step-by-step explanation:
This is by the simple quantum physics moving by the gravitational carbon dioxide in the air that causes the numbers to evolve into the number 11 while mixed together
if the active ingredient in a lotion is of the strength 23 ppm, how many milligrams of the active ingredient are in 1 liter of the lotion? round answer to the nearest whole number. (ch. 6 in calc).
Answers
One liter of the lotion contains 23 milligrams of the active ingredient.
If the active ingredient in a lotion uses the Strength 23 ppm (parts per million)
Definition of PPM ?
The best approach to describe the degree of performance or chemical concentration in a larger combination is in parts per million, or PPM. This could be used to describe the components of water, the faulty rate of a provider, etc. Being a ratio of two quantities of the same unit, it is theoretically a dimensionless measure that is represented as a percentage and is better suited to representing lesser concentrations of chemicals in gases, liquids, or solids. In its entire form, one part per million (ppm) is written as equation ppm=1/1,000,000=0.0001 /eq% of the whole.
1gm = 1000 mg
1 litre = 1000 ml
So that
1 ppm = 1 mg per liter
1 ppm = 0.998
23 ppm = 23 x 0.998
23 ppm = 22.958 mg / L
It is approximately equal to 23 mg / L
Round off to the nearest whole no 23 p pm = 23 mg / L
Therefore, 23 mg of active ingredient are in 1 liter of the lotion
To learn more about equation click here:
brainly.com/question/2228446
#SPJ4
10.6.3 Test (CST): Factoring Polynomials
Question 3 of 25
What are the zeros of f(x) = x²-x-20?
OA. x=-2 and x = 10
B. x= -4 and x = 5
OC. x=-10 and x = 2
OD. x= -5 and x = 4
Answers
Therefore, the zeros of the function f(x) are x = 5 and x = -4.
What is polynomial?A polynomial is a mathematical expression consisting of variables and coefficients, combined using the operations of addition, subtraction, multiplication, and non-negative integer exponents. It can have one or more terms, and the degree of a polynomial is the highest power of the variable in the expression.
Here,
To find the zeros of the function f(x) = x² - x - 20, we need to solve for x when f(x) = 0:
x² - x - 20 = 0
We can factor the left side of this equation as:
(x - 5)(x + 4) = 0
Using the zero product property, we know that the product of two factors is zero if and only if at least one of the factors is zero. Therefore, we can set each factor equal to zero and solve for x:
x - 5 = 0 or x + 4 = 0
Solving for x in each equation gives us:
x = 5 or x = -4
To know more about polynomial,
https://brainly.com/question/11536910
#SPJ1
In the future, the DSM may change to a dimensional approach for the diagnosis of personality disorders. What action will be required of clinicians
Answers
If the DSM changes to a dimensional approach for diagnosing personality disorders in the future, clinicians will need to adapt their diagnostic practices by using a different framework that emphasizes the continuum of symptoms and traits, rather than categorical diagnoses.
If the DSM (Diagnostic and Statistical Manual of Mental Disorders) transitions to a dimensional approach for personality disorders, clinicians will need to adjust their diagnostic strategies accordingly. Currently, the DSM employs a categorical model, where individuals either meet the criteria for a specific disorder or they do not. However, a dimensional approach would shift the focus towards assessing the severity and variability of symptoms and traits across a spectrum.
To adapt to this change, clinicians will require training and education on the new dimensional framework. They will need to familiarize themselves with the new diagnostic criteria and learn how to assess and measure the various dimensions of personality functioning. This may involve using standardized assessment tools and scales that capture different facets of personality, such as neuroticism, extraversion, or conscientiousness.
Clinicians will also need to develop a nuanced understanding of how these dimensions interact with each other and with other mental health conditions. They will have to consider the interplay between different personality traits and how they contribute to the overall functioning and well-being of individuals. Additionally, treatment planning and interventions may need to be adjusted to align with the dimensional framework, focusing on addressing specific areas of impairment or dysfunction rather than solely targeting categorical diagnoses.
Overall, the shift to a dimensional approach in the DSM for personality disorders would require clinicians to adapt their diagnostic practices by embracing a more nuanced and comprehensive understanding of personality functioning. It would involve incorporating dimensional assessments, updating their knowledge base, and refining treatment approaches to better align with the new framework.
Learn more about personality disorders here:
https://brainly.com/question/31800439
#SPJ11
what is the value of 3.5(11)+1.9(11)+1.6(11)
Answers
Answer:
77
Step-by-step explanation:
3.5 ( 11 ) = 38.5
1.9 ( 11 ) = 20.9
1.6 ( 11 ) = 17.6
38.5 + 20.9 + 17.6
= 77
hope this helps