The World Health Organization (WHO) stated that 53% of women who had a caesarean section for childbirth in a current year were over the age of 35. Fifteen caesarean section patients are sampled. a) Calculate the probability that i) exactly 9 of them are over the age of 35 ii) more than 10 are over the age of 35 iii) fewer than 8 are over the age of 35 b) Clarify that would it be unusual if all of them were over the age of 35? c) Present the mean and standard deviation of the number of women over the age of 35 in a sample of 15 caesarean section patients. 5. Advances in medical and technological innovations have led to the availability of numerous medical services, including a variety of cosmetic surgeries that are gaining popularity, from minimal and noninvasive procedures to major plastic surgeries. According to a survey on appearance and plastic surgeries in South Korea, 20% of the female respondents had the highest experience undergoing plastic surgery, in a random sample of 100 female respondents. By using the Poisson formula, calculate the probability that the number of female respondents is a) exactly 25 will do the plastic surgery b) at most 8 will do the plastic surgery c) 15 to 20 will do the plastic surgery
Answers
The final answers:
a)
i) Probability that exactly 9 of them are over the age of 35:
P(X = 9) = (15 C 9) * (0.53^9) * (1 - 0.53)^(15 - 9) ≈ 0.275
ii) Probability that more than 10 are over the age of 35:
P(X > 10) = P(X = 11) + P(X = 12) + ... + P(X = 15) ≈ 0.705
iii) Probability that fewer than 8 are over the age of 35:
P(X < 8) = P(X = 0) + P(X = 1) + ... + P(X = 7) ≈ 0.054
b) To determine whether it would be unusual if all 15 women were over the age of 35, we calculate the probability of this event happening:
P(X = 15) = (15 C 15) * (0.53^15) * (1 - 0.53)^(15 - 15) ≈ 0.019
Since the probability is low (less than 0.05), it would be considered unusual if all 15 women were over the age of 35.
c) Mean and standard deviation:
Mean (μ) = n * p = 15 * 0.53 ≈ 7.95
Standard Deviation (σ) = sqrt(n * p * (1 - p)) = sqrt(15 * 0.53 * (1 - 0.53)) ≈ 1.93
5. Using the Poisson formula for the plastic surgery scenario:
a) Probability that exactly 25 respondents will do plastic surgery:
λ = n * p = 100 * 0.2 = 20
P(X = 25) = (e^(-λ) * λ^25) / 25! ≈ 0.069
b) Probability that at most 8 respondents will do plastic surgery:
P(X ≤ 8) = P(X = 0) + P(X = 1) + ... + P(X = 8) ≈ 0.047
c) Probability that 15 to 20 respondents will do plastic surgery:
P(15 ≤ X ≤ 20) = P(X = 15) + P(X = 16) + ... + P(X = 20) ≈ 0.666
a) To calculate the probability for each scenario, we will use the binomial probability formula:
\(P(X = k) = (n C k) * p^k * (1 - p)^(n - k)\)
Where:
n = total number of trials (sample size)
k = number of successful trials (number of women over the age of 35)
p = probability of success (proportion of women over the age of 35)
Given:
n = 15 (sample size)
p = 0.53 (proportion of women over the age of 35)
i) Probability that exactly 9 of them are over the age of 35:
P(X = 9) = (15 C 9) * (0.53^9) * (1 - 0.53)^(15 - 9)
ii) Probability that more than 10 are over the age of 35:
P(X > 10) = P(X = 11) + P(X = 12) + ... + P(X = 15)
= Summation of [(15 C k) * (0.53^k) * (1 - 0.53)^(15 - k)] for k = 11 to 15
iii) Probability that fewer than 8 are over the age of 35:
P(X < 8) = P(X = 0) + P(X = 1) + ... + P(X = 7)
= Summation of [(15 C k) * (0.53^k) * (1 - 0.53)^(15 - k)] for k = 0 to 7
b) To determine whether it would be unusual if all 15 women were over the age of 35, we need to calculate the probability of this event happening:
P(X = 15) = (15 C 15) * (0.53^15) * (1 - 0.53)^(15 - 15)
c) To calculate the mean (expected value) and standard deviation of the number of women over the age of 35, we can use the following formulas:
Mean (μ) = n * p
Standard Deviation (σ) = sqrt(n * p * (1 - p))
For the given scenario:
Mean (μ) = 15 * 0.53
Standard Deviation (σ) = sqrt(15 * 0.53 * (1 - 0.53))
5. Using the Poisson formula for the plastic surgery scenario:
a) To calculate the probability that exactly 25 respondents will do plastic surgery, we can use the Poisson probability formula:
P(X = 25) = (e^(-λ) * λ^25) / 25!
Where:
λ = mean (expected value) of the Poisson distribution
In this case, λ = n * p, where n = 100 (sample size) and p = 0.2 (proportion of female respondents undergoing plastic surgery).
b) To calculate the probability that at most 8 respondents will do plastic surgery, we sum the probabilities of having 0, 1, 2, ..., 8 respondents undergoing plastic surgery:
P(X ≤ 8) = P(X = 0) + P(X = 1) + ... + P(X = 8)
c) To calculate the probability that 15 to 20 respondents will do plastic surgery, we sum the probabilities of having 15, 16, 17, 18, 19, and 20 respondents undergoing plastic surgery:
P(15 ≤ X ≤ 20) = P(X = 15) + P(X = 16) + ...
To know more about "Probability" refer here:
brainly.com/question/30034780#
#SPJ4
Related Questions
A large company put out an advertisement in a magazine for a job
opening. The first day the magazine was published the company got 90
responses, but the responses were declining by 10% each day.
Assuming the pattern continued, how many total responses would the
company get over the course of the first 19 days after the magazine was
published, to the nearest whole number?
Answers
Answer:
C(19)=12 responses
Step-by-step explanation:
Exponential Decay Function
The exponential function is frequently used to model natural growing or decaying processes, where the change is proportional to the actual quantity.
An exponential decaying function can be expressed as follows:
\(C(t)=C_o\cdot(1-r)^t\)
Where:
C(t) is the actual value of the function at time t
Co is the initial value of C at t=0
r is the decaying rate, expressed in decimal
The company puts out an advertisement for a job opening. Initially, the company got 90 responses to the advertisement. Each day, the responses declined by 10%.
This is an example where the decay model can be used to calculate the responses to the advertisement at the day t.
The initial value is Co=90, the decaying rate is r=10% = 0.10. The model is written as:
\(C(t)=90\cdot(1-0.1)^t\)
Calculating:
\(C(t)=90\cdot(0.9)^t\)
We are required to calculate the number of responses at day t=19, thus:
\(C(19)=90\cdot(0.9)^{19}\)
C(19)=12 responses
Harden is building shelves for his comic book collection. He has a piece of wood that is 3.5 feet long. After cutting four equal pieces of wood from it, he has 0.6 feet of wood left over.
Part A: Write an equation that could be used to determine the length of each of the four pieces of wood he cut
Part B: Explain how you know the equation from part A is correct
Part C: Solve the equation from Part A. Show every step of your work.
Answers
The length of each piece of wood is 0.725 feet.
We are given that the Length= 3.5feet
Now,
This is a word problem that can be solved by using algebra and arithmetic.
Part A: Let x be the length of each of the four pieces of wood he cut. Then, according to the problem, we have:
4x + 0.6 = 3.5
This is the equation that could be used to determine the length of each piece of wood.
Part B: We know the equation from part A is correct because it represents the total length of the wood before and after cutting. The left side of the equation is the sum of the lengths of the four pieces of wood and the leftover piece of wood. The right side of the equation is the original length of the wood. Since cutting does not change the total length of the wood, these two sides must be equal.
Part C: To solve the equation from part A, we need to isolate x by using inverse operations. We get:
4x + 0.6 = 3.5 4x = 3.5 - 0.6 (subtract 0.6 from both sides) 4x = 2.9 x = 2.9/4 (divide both sides by 4) x = 0.725
Therefore, by the algebra the answer will be 0.725 feet.
More about the Algebra link is given below.
brainly.com/question/953809
#SPJ1
Marking Brainliest. Can someone please how to do this with a fairly simple explanation? I'm not sure what to do.

Answers
Explanation:
In the LS column, you'll have these steps
3x - 1
3*4 - 1
12 - 1
11
Effectively, we replaced x with 4 and then simplified using PEMDAS.
And in the RS column, you'll have these steps
x + 7
4 + 7
11
We get the same thing at the bottom of each column. This shows that we end up with 11 = 11 after simplifying both sides. Therefore, we've confirmed that x = 4 is the solution to 3x - 1 = x + 7

x^3x^5=x^p, where p=
Answers
Here, we use the property of multiplication of exponential expression which states when we multiply two exponential expressions with the same base, we keep the base and add the exponents.
Therefore,
\(x^(3+5) = x^8\)
Now,
\(x^(3+5) = x^8\)
is of the form:
\(x^b = x^p\)
When we have two equal expressions on either side of the equation, the power of the base remains the same. Therefore,
p = 8
There we have it. The value of p is 8. The full solution is shown below:
\(x^3 × x^5 \\= x^px^8\\ = x^p\)
We can see that the base of the exponential expression on either side is equal.
Therefore, the power of the base must be equal as well. In other words
,p = 8.
To know more about base visit:
https://brainly.com/question/14291917
#SPJ11
pls help me with this thnx

Answers
Answer:
Shop B has a better value for their baked beans.
Step-by-step explanation:
Shop A:
5 kg = 5.65
1 kg = 5.65 / 5
= 1.13 pence
Shop B:
2 kg = 2.02
1 kg = 2.02 / 2
= 1.01 pence
There's a roughly linear relationship between the number of times a species of cricket will chirp in one minute and the temperature outside. For a certain type of cricket, this relationship can be expressed using the formula T = 0.31c + 36,

Answers
Explain how the distance formula can be used to find the diameter of a circle?
Answers
Answer: A line segment connecting two points on the circle and going through the center is called a diameter of the circle. ... Use the Distance Formula to find the equation of the circle. √(x2−x1)2+(y2−y1)2=d. Substitute (x1,y1)=(h,k),(x2,y2)=(x,y) and d=r .
The table represents an inverse variation. What is the value of p?
x 3 10 15 30
y 5 p 1 0. 5
Answers
The value of p is 1.5 for which the table shows inverse relation.
For inverse relation between x and y we assume any function then check it with the given values and find the variable in the equation.
so let the equation is:
y = \(\frac{k}{x^n}\) ------(i)
where k and n are variables which we have to find using the given data
for case 1 y=5 and x=3
after assigning the values in equation (i) we get
5 = \(\frac{k}{3^n}\) ------(ii)
for case 3 , y= 15 and x=1;
after assigning the values in equation 1 we get:
15 =\(\frac{k}{1^n}\) -------(iii)
dividing equation (ii) and (i) we get
3 = \(3^n\)
=> n=1
so equation (i) reduces to
y= \(\frac{k}{x}\)
putting y=3 and x=5 in the above equation we get
3 = k/5
=> k = 15
so the final equation we got is :
y = \(\frac{15}{x}\) -------(iv)
now in case 2 we are given y=p and x=10
after assigning the values in equation (iv) we get
p = 15/10
=> p= 1.5
so the value of p =1.5
To know more about inverse relation click on below link:
https://brainly.com/question/2501331#
#SPJ4
Find the volume V of the solid below the paraboloid z=8−x^2−y^2 and above the following region. R={(r,θ):1≤r≤2,−π/2≤θ≤π/2}
Answers
Volume of the solid below the paraboloid z = 8 - x^2 - y^2 and above the region R = {(r, θ): 1 ≤ r ≤ 2, -π/2 ≤ θ ≤ π/2} is [4/3]π cubic units.
To find the volume of the solid below the paraboloid z = 8 - x^2 - y^2 and above the region R = {(r, θ): 1 ≤ r ≤ 2, -π/2 ≤ θ ≤ π/2}, we can use a double integral in polar coordinates.
In polar coordinates, the volume element becomes dV = r dr dθ.
The limits of integration for r are from 1 to 2, and the limits of integration for θ are from -π/2 to π/2.
The volume V can be calculated as follows:
V = ∫∫R (8 - r^2) r dr dθ
= ∫[-π/2, π/2] ∫[1, 2] (8 - r^2) r dr dθ
Integrating with respect to r first:
V = ∫[-π/2, π/2] [4r^2 - (1/3)r^4] from 1 to 2 dθ
= ∫[-π/2, π/2] [(4(2)^2 - (1/3)(2)^4) - (4(1)^2 - (1/3)(1)^4)] dθ
= ∫[-π/2, π/2] [16/3 - 4/3] dθ
= ∫[-π/2, π/2] [4/3] dθ
= [4/3]θ from -π/2 to π/2
= [4/3](π/2 + π/2)
= [4/3]π
Learn more about volume here:
https://brainly.com/question/13338592
#SPJ11
Solve the system by elimination.
3x + 3 = 3y
2x - 6y = 2
Answers
Answer:
The Point Form is: (-2,-1)
Equation form is x= -2, y = -1
Step-by-step explanation:
Answer:
(-2, -1)
Step-by-step explanation:
both equation form: Ax + By = C
3x - 3y = -3 - 2×(3x - 3y = -3) = 6x + 6y = 6
2x - 6y = 2 - Terms opposite = 2x - 6y = 2
( Add) - 4x = 8
divide by -4 = x = -2
Put X value in equations 3(-2) + 3 = 3y and solve -
-6 + 3 = 3y
-3 = 3y
-1 = y
Answer= (-2, -1)
What is the volume of the cylinder?
•576 cm3
•2887 cm3
•96 cm3
•192 cm3

Answers
\( \large\begin{gathered} {\underline{\boxed{ \rm {\red{Volume \: \: of \: \: cylinder \: = \: \pi \: {r}^{2} \: h }}}}}\end{gathered}\)
r represents radius of cylinder.h represents height of cylinder.So ,r = 6 cmh = 16 cmπ = 3.14Substuting the values⇥Volume of the cylinder = π r² h
⇥Volume of the cylinder = 3.14 × 36 × 16
⇥Volume of the cylinder = 113.04 × 16
⇥Volume of the cylinder = 1808.64
Hence , the volume of cylinder is 1808.64 cm²
A microwave is placed on top of two boxes. One box is 2 feet 10 inches tall, the other box is 4 feet 7 inches tall, and the microwave is 3 feet 4 inches tall. How tall are they combined? Write your answer in feet and inches. Use a number less than 12 for inches.
Answers
Answer:
10 feet 9 inches.
Step-by-step explanation:
(24+10)+(48+7)+(36+4)
34+55+40
129 inches
10 feet 9 inches
A circle has a circumference of 6. It has an arc of length 1.
What is the central angle of the arc, in degrees?
Answers
The circumference formula for a circle is C=πd where C is the circumference, d is the diameter of the circle and π is a constant. If you plug in 6 for C and solve the equation for d like:
6= πd and then divide both sides of the equation by π you get that d = 1.90
To find the central angle of an arc you would use the equation S = rθ where S is the length of the arc, r is the radius of the circle, and θ is the measure of the angle which in this case is unknown. So with S = 1 and r = d/2 = 1.90/2 = 0.9549 you would have an equation that looks like this:
1 = 0.9549θ
Answer:
60
Step-by-step explanation:
1/6 x 360
Central angle is equal to measure of intercepted arc.
60 degrees
PLEASE HELP!!! Line I is a reflection of line k. Write an equation that
represents line k.

Answers
Answer:
y=-2
Step-by-step explanation:
I am assuming the equation is asking for a reflection over the y-axis.
When you reflect across the y-axis it becomes the negative version of itself.
what is the length and width of a basketball court
Answers
The length of a standard basketball court is 94 feet (28.65 meters), and the width is 50 feet (15.24 meters).
A standard basketball court is rectangular in shape and follows certain dimensions specified by the International Basketball Federation (FIBA) and the National Basketball Association (NBA). The length and width of a basketball court may vary slightly depending on the governing body and the level of play, but the most commonly used dimensions are as follows:
The length of a basketball court is typically 94 feet (28.65 meters) in professional settings. This length is measured from baseline to baseline, parallel to the sidelines.
The width of a basketball court is usually 50 feet (15.24 meters). This width is measured from sideline to sideline, perpendicular to the baselines.
These dimensions provide a standardized playing area for basketball games, ensuring consistency across different courts and facilitating fair play. It's important to note that while these measurements represent the standard dimensions, there can be slight variations in court size depending on factors such as the venue, league, or specific regulations in different countries.
Learn more about rectangular here:
https://brainly.com/question/21416050
#SPJ11
Dave is trying on pants. Each pair is too small, fits well, or is too big. Dave estimates that 10%, percent of the pants he tries on will be too small and that 20% of the pants will be too big. If he were to try on 20 pairs of pants, which is the best prediction for the number of pairs of pants that would fit well?
Answers
The best prediction for the number of pair of pants that would fit well is 14.
What is the best prediction?Percentage is when value is converted to a number out of 100. Percentage is a measure of frequency. The sign that is used to represent percentages is %.
The first step is to determine the percentage of pair of pants that would fit well.
Percentage of the pair of pants that would fit well = 100% - percentage that are too big - percentage that are too small
Percentage of the pair of pants that would fit well = 100% - 10% - 20% = 70%
Number of pair of pants that would fit well = total pants that Dave tried x percentage that fits well
Number of pair of pants that would fit well = 20 x 70%
Number of pair of pants that would fit well = 20 x 0.7 = 14
To learn more about percentages, please check:
https://brainly.com/question/25764815
#SPJ1
Select the correct answer from the drop-down menu. There are two numbers. One number is twice the other number. The difference of the smaller number and half the larger number is 20. An equation created to find the smaller number will have .
Answers
Answer: The correct answer is no solution.
The required equation created to find the smaller number will be expressed as x - y/2 = 20 where x is the smaller number.
Let the two unknown numbers be x and y;
The smaller number is x
The larger number is y
If one number is twice the other number, hence;
y = 2x ................. 1
Also, if the difference of the smaller number and half the larger number is 20, then:
x - y/2 = 20 .................. 2
Substitute the equation 1 into 2 to have:
x - (2x/2) = 20
x - x = 20
Hence the required equation created to find the smaller number will be expressed as x - y/2 = 20 where x is the smaller number.
Learn more here; https://brainly.com/question/13805464
How do you find the horizontal and vertical asymptote of a curve?
Answers
Answer: search it up
Step-by-step explanation:
Task 9: Cookie Jar Problem There was a jar of cookies on the table. Latoya was hungry because she hadn't had breakfast, so she took half of the cookies. Then Mark came along and noticed the cookies. He thought they looked good, so he ate a third of what was left in the jar. Kandi came by and decided to take a fourth of the remaining cookies with her to her next class. Then Shannon came dashing up and took a cookie to munch on. When Michelle looked at the cookie jar, she saw that there were two cookies left. "How many cookies were there in the jar, to begin with?" she asked Kira.
Extension: If there were 2/3 of a cookie left over, how many cookies were there before Latoya came?
Can you please explain the work too, please!
Answers
The number of cookies in the jar initially was 42
To find out how many cookies were in the jar initially, we can use algebra to represent the problem. Let x be the number of cookies in the jar initially. After Latoya took half of the cookies, Mark took 1/3 of the remaining cookies, Kandi took 1/4 of the remaining cookies, and Shannon took 1 cookie, there are 2 cookies left in the jar.
We can use this information to set up the equation:
x/2 - (x/2)/3 - (x/2)/4 - 1 - 2 = 0.
By solving this equation, we get x = 42. This means there were 42 cookies in the jar initially. To find out how many cookies were there before Latoya came, we just add the 2/3 of a cookie that was left over to the 2 whole cookies we know of.
So, 42+2/3 = 42.67 which means 42 cookies were there before Latoya came.
For more questions like Cookies click the link below:
https://brainly.com/question/26252639
#SPJ4
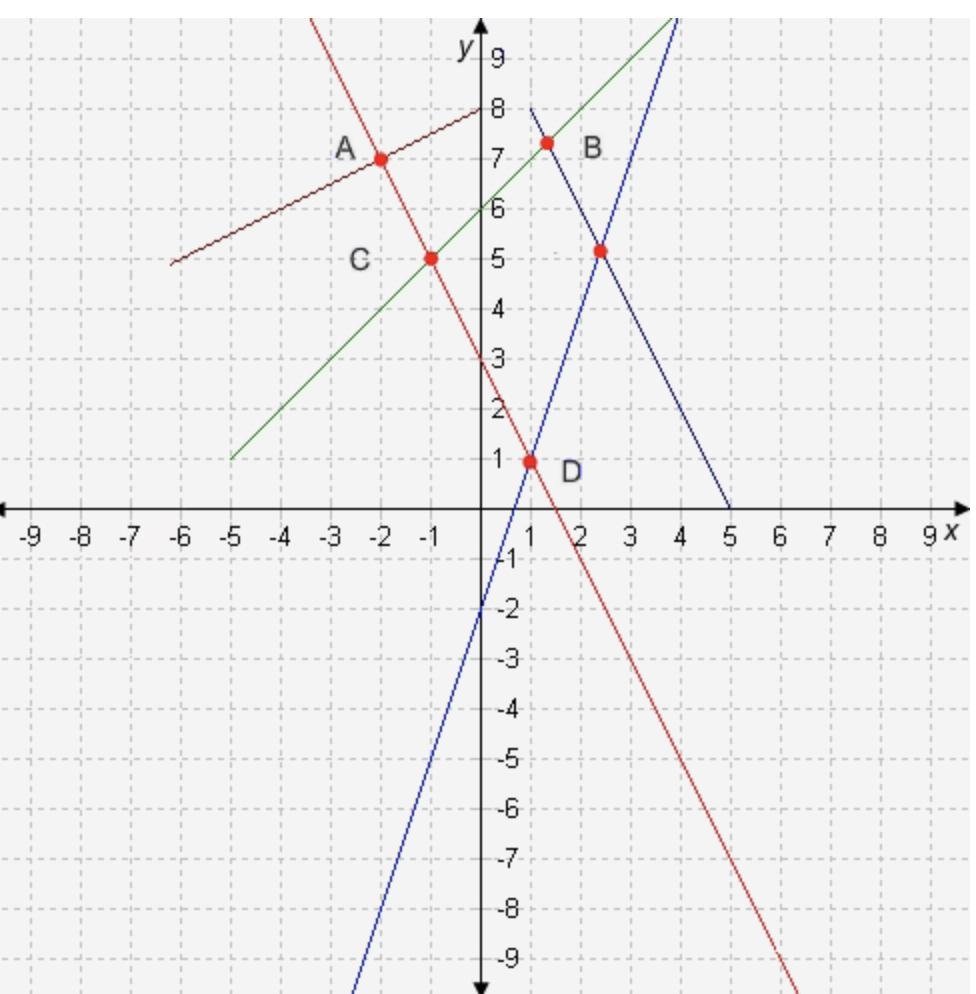
Which point satisfies the system of equations y = 3x − 2 and y = -2x + 3?
Answers
Point D with coordinates (1 , 1) satisfies the system of equations .
solution in attachment.

Answer:
(1, 1) Point D satisfies the system of equations y=3x-2 and y=-2x+3.
Step-by-step explanation:
y=3x-2
y=-2x+3
---------------
3x-2=-2x+3
3x-(-2x)-2=3
3x+2x-2=3
5x-2=3
5x=3+2
5x=5
x=5/5
x=1
y=3(1)-2=3-2=1
on the math portion of the sat, scores are roughly normal, with a mean of 500 and a standard deviation of 100. what percent of scores are above 400?
Answers
The percent of scores are above 400 is 84.13 percent.
Given that, mean \((\bar{x})\)=500 and the standard deviation \((\sigma)\)=100.
Standard deviation is the positive square root of the variance. Standard deviation is one of the basic methods of statistical analysis. Standard deviation is commonly abbreviated as SD and denoted by 'σ’ and it tells about the value that how much it has deviated from the mean value.
Here, from the normalization curve the proportion of SAT scores above 400 is
\((50+\frac{68.26}{2})\%\)
\(= 84.13 \%\)
Therefore, the percent of scores are above 400 is 84.13 percent.
Learn more about the standard deviation visit:
brainly.com/question/13905583.
#SPJ12

Pls Help lol (50pts) :))

Answers
Answer:
the answer is b
Step-by-step explanation:
1. Breaks are applied to a train traveling at 40 m/s and after 8 seconds of constant deceleration it comes to a halt. How far did the train travel during this time?
2. Find the area of the region between the curve y = 1/1+x^2 0≤ x ≤ √3, and the x-axis.
Answers
Therefore, the area of the region between the curve \(y = 1/(1+x^2),\) 0 ≤ x ≤ √3, and the x-axis is ln(2) square units.
To find the distance traveled by the train during the deceleration, we can use the formula for distance covered under constant deceleration:
distance = initial velocity * time + (1/2) * acceleration * time²
In this case, the initial velocity of the train is 40 m/s, and it comes to a halt after 8 seconds. The deceleration is constant.
Since the train comes to a halt, its final velocity is 0 m/s. We can calculate the deceleration using the formula:
final velocity = initial velocity + (acceleration * time)
0 = 40 + (acceleration * 8)
Solving for acceleration, we get:
acceleration = -40/8 = -5 m/s²
Now, we can plug in the values into the distance formula:
distance = 40 * 8 + (1/2) * (-5) * 8²
= 320 + (-20) * 64
= 320 - 1280
= -960 meters
The negative sign indicates that the train traveled in the opposite direction of its initial velocity.
Therefore, the train traveled a distance of 960 meters during the 8 seconds of constant deceleration.
To find the area of the region between the curve \(y = 1/(1+x^2)\), 0 ≤ x ≤ √3, and the x-axis, we can integrate the function with respect to x over the given interval.
The area can be calculated using the definite integral:
Area = ∫[0, √3] (1/(1+x²)) dx
To evaluate this integral, we can use a substitution. Let u = 1+x², then du = 2x dx.
Rewriting the integral with the substitution, we have:
Area = ∫[0, √3] (1/u) * (1/2x) du
Simplifying, we get:
Area = (1/2) ∫[0, √3] (1/u) du
Taking the antiderivative, we have:
Area = (1/2) ln|u| + C
Now, we need to substitute the original variable x back in:
Area = (1/2) ln|1+x²| + C
To find the definite integral, we evaluate the antiderivative at the upper and lower limits:
Area = (1/2) ln|1+√3²| - (1/2) ln|1+0²|
= (1/2) ln(1+3) - (1/2) ln(1+0)
= (1/2) ln(4) - (1/2) ln(1)
= (1/2) ln(4)
= ln(2)
To know more about area,
https://brainly.com/question/33373762
#SPJ11
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 Make a list of all the patterns you notice in the number arrangement above. If we were to continue this number arrangement, what would be the middle number on the 50th row? What about the nth row?
Answers
Answer:
chronological
or +1 each number up
Step-by-step explanation:
The middle number on the 50th row is 891.5.
The nth row is 18n - 17.
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
We see that there are 18 numbers in each row.
The numbers are consecutive natural numbers.
Now,
We can see that,
The first number of each row is 1.
The first number of the second row is 19.
The first number of the third row is 37.
The first number in each row can form a series.
1, 19, 37,....
This series is an arithmetic sequence.
First term = 1
Common difference = 18
The nth term is a + (n - 1)d.
50th term.
= 1 + (50 - 1)18
= 1 + 49 x 18
= 1 + 882
= 883
This means,
The 50th row will have the following series.
883, 884, 885, 886, 887, 888, 889, 890, 891, 892, 893, 894, 895, 896, 897, 898, 899, 900.
The middle number is the midpoint of 891 and 892.
= 891.5
The nth row.
= 1 + (n - 1)18
= 1 + 18n - 18
= 18n - 17
Thus,
The middle number on the 50th row is 891.5.
The nth row is 18n - 17.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ2
Please I’m in some need of help lol

Answers
The width of a rectangle is 5y -4.5 feet and the length is 4.5y +6 feet. Find the perimeter of the rectangle
pls in 5 min hurry
Answers
Answer:
19y+3
Step-by-step explanation:
The equation for perimeter is:
\(2(l+w)\)
Plug in the values into the equation:
\(2(4.5y+6+5y-4.5)=2(9.5y+1.5)=19y+3\)
what is the probability that the number of calls among the 25 that involve a fax transmission exceeds the expected number by more than 2 standard deviations? (round your answer to three decimal places.)
Answers
0.003 is the probability that the number of calls among the 25 that involve a fax transmission exceeds the expected number by more than 2 standard deviations
To calculate the probability that the number of calls among the 25 that involve a fax transmission exceeds the expected number by more than 2 standard deviations.The mean is the expected number of calls involving a fax transmission, while the standard deviation is the measure of variability in the distribution. We then use this information to calculate the probability of exceeding the expected number by more than 2 standard deviations, which can be done using the z-score formula. The z-score for values more than 2 standard deviations away from the mean is 2.33, which corresponds to a probability of 0.003. Thus, the probability that the number of calls among the 25 that involve a fax transmission exceeds the expected number by more than 2 standard deviations is 0.003.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
I need the endear for number six. Will give brainliest for help/answer.

Answers
Answer:
f(1) = 2, f(4) = 8
Step-by-step explanation:
f(1) in the interval - 3 < x ≤ 1 , then f(x) = x + 1 , so
f(1) = 1 + 1 = 2
f(4) in the interval 1 < x ≤ 4 , then f(x) = 2x , so
f(4) = 2 × 4 = 8
For what value of k is the expression x^4 + kx^2 + 49 a perfect square?
Answers
Answer:
\(k=14\)
Step-by-step explanation:
Completing the square gives
\(x^4 + kx^2 + 49\\= (x^2+7)^2 - 14x^2 + kx^2\)
So we have to cancel the latter two terms out for the expression to always become a square (otherwise we are dealing with a square plus something else, which doesn't always result in a square), giving us our answer directly.
Answer:
k=± 14
Step-by-step explanation:
\(x^4+kx^2+49\\Disc.=b^2-4ac=k^2-4*1*49\\it ~ is ~a ~ perfect ~ square.\\k^2-196=0\\k^2=196\\k= \pm 14\)
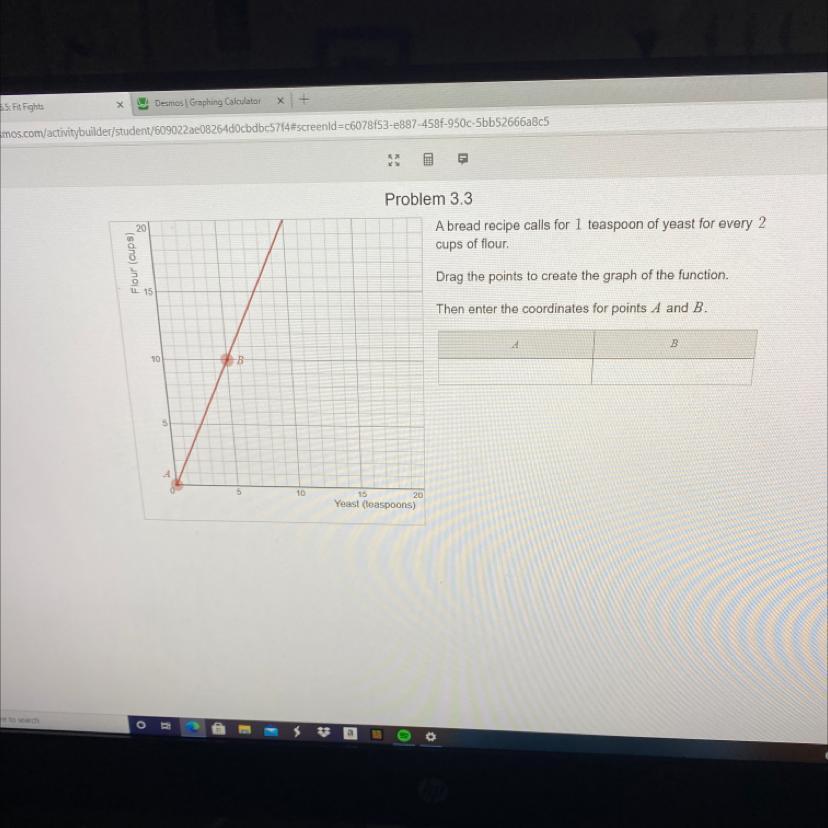
A bread recipe calls for 1 teaspoon of yeast for every 2
cups of flour.
Drag the points to create the graph of the function.
Then enter the coordinates for points A and B.
Answers
The Coordinates for point A and B are as follows:
A B
1 2
2 4
3 6
What is Coordinates system?A coordinate system is a method for identifying the location of a point on the earth. Most coordinate systems use two numbers, a coordinate, to identify the location of a point.
The Coordinates for point A and B are as follows:
A B
1 2
2 4
3 6
4 8
5 10
6 12
7 14
8 16
9 18
10 20
Thus, y-coordinates are double than x-coordinates.
Learn more about Coordinate system from:
https://brainly.com/question/4726772
#SPJ2