Answers
Answer:yes they do
Step-by-step explanation:
Related Questions
the directions are : The table shows a proportional relationship between x and y. What is the unit rate of y per x.
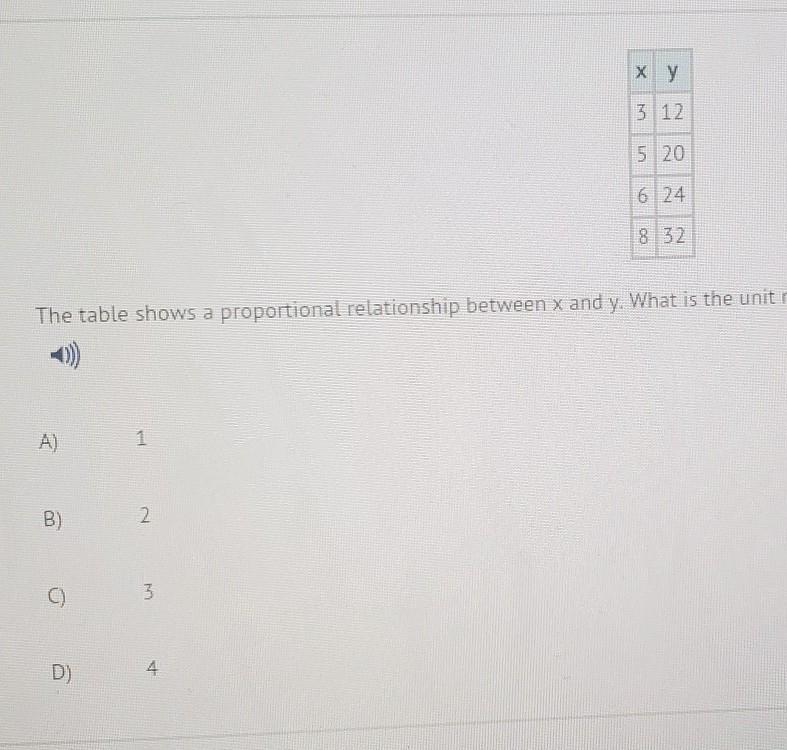
Answers
Answer:
4
Step-by-step explanation:
To find the unit rate you can pick any row and do y divided by x
For example, x = 3 and y = 12 so you can do 12 / 3 = 4.
You could also use x = 5 and y = 20, so it would be 20 / 5 = 5
What is the product of 5/10 x 4/5 in lower terms (simplified)?*
A.20/5
B.2/5
C.9/15
D.10/25
Answers
Answer:
\(\frac{2}{5}\)
Step-by-step explanation:
We have two fractions being multiplied and are being asked to simplify it.
When you multiply two fractions, you always multiply across :
\(\frac{5}{10}*\frac{4}{5} = \frac{5*4}{10*5}\)
\(\frac{20}{50}\)
Since both the numerator and denominator end in 0, we can simplify this by cutting out the zeroes.
Leaving us with B. 2/5
Conrad is reading a blue print to make a shed. On the blue print, the length of the shed is 12 inches and the ramp attached to the shed is 1 inch. He wants to convert the total length of the shed and ramp from inches to yards. Select all of the expressions which correctly show how to convert the length of the shed and ramp from inches to yards using the ratio 36 inches to 1 yard.
Answers
To convert inches to yards, we need to divide by 36, since 36 inches make 1 yard. Therefore, to convert the length of the shed and ramp from inches to yards, we can use the following expressions: (12 + 1) / 36 = 0.3611... yards, (12 / 36) + (1 / 36) = 0.3611... yards, 13 / 36 = 0.3611... yards
What are expressions?An expression in mathematics is a grouping of variables, numbers, and actions that can be evaluated to yield a value. A wide range of mathematical notions, from basic arithmetic computations to intricate algebraic formulas and beyond, are represented by expressions.
These components can be used to combine expressions in a wide range of different ways. For instance, we can construct straightforward arithmetic phrases such as "2 + 3" or "5 * 4" or more intricate algebraic expressions such as "3x2 + 2x + 1" or "sin(x) + cos(x)". In each instance, the expression denotes a mathematical idea that may be tested to provide a certain value.
Expressions play a significant role in mathematics and are utilized in a wide range of fields in science, engineering, and finance. By being aware of how expressions work, we can better understand and solve a wide variety of mathematical problems.
To know more about expressions visit:
https://brainly.com/question/14083225
#SPJ1
Let Y1 and Y2 denote the proportion of time during which employees I and II actually performed their assigned tasks during a workday, The joint density of Y1 and Y2 is given by
f(y1,y2) = { y1+y2, 0<=y1<=1, 0<=y2<=1, 0, elsewhere
Required:
a. Find the marginal density function of Y1 and Y2
b. Find P(Y1 >= 1/2 | Y2 >= 1/2).
c. If employee II spends exactly 50% of the dayworking on assigned duties, find the probability that employee I spends more than 75% of the day working on similarduties.
Answers
Answer:
Step-by-step explanation:
From the information given:
The joint density of \(y_1\) and \(y_2\) is given by:
\(f_{(y_1,y_2)} \left \{ {{y_1+y_2, \ \ 0\ \le \ y_1 \ \le 1 , \ \ 0 \ \ \le y_2 \ \ \le 1} \atop {0, \ \ \ elsewhere \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \right.\)
a)To find the marginal density of \(y_1\).
\(f_{y_1} (y_1) = \int \limits ^{\infty}_{-\infty} f_{y_1,y_2} (y_1 >y_2) \ dy_2\)
\(=\int \limits ^{1}_{0}(y_1+y_2)\ dy_2\)
\(=\int \limits ^{1}_{0} \ \ y_1dy_2+ \int \limits ^{1}_{0} \ y_2 dy_2\)
\(= y_1 \ \int \limits ^{1}_{0} dy_2+ \int \limits ^{1}_{0} \ y_2 dy_2\)
\(= y_1[y_2]^1_0 + \bigg [ \dfrac{y_2^2}{2}\bigg]^1_0\)
\(= y_1 [1] + [\dfrac{1}{2}]\)
\(= y_1 + \dfrac{1}{2}\)
i.e.
\(f_{(y_1}(y_1)}= \left \{ {{y_1+\dfrac{1}{2}, \ \ 0\ \ \le \ y_1 \ \le , \ 1} \atop {0, \ \ \ elsewhere \ \\ \ \ \ \ \ \ \ \ } \right.\)
The marginal density of \(y_2\) is:
\(f_{y_1} (y_2) = \int \limits ^{\infty}_{-\infty} fy_1y_1(y_1-y_2) dy_1\)
\(= \int \limits ^1_0 \ y_1 dy_1 + y_2 \int \limits ^1_0 dy_1\)
\(=\bigg[ \dfrac{y_1^2}{2} \bigg]^1_0 + y_2 [y_1]^1_0\)
\(= [ \dfrac{1}{2}] + y_2 [1]\)
\(= y_2 + \dfrac{1}{2}\)
i.e.
\(f_{(y_1}(y_2)}= \left \{ {{y_2+\dfrac{1}{2}, \ \ 0\ \ \le \ y_1 \ \le , \ 1} \atop {0, \ \ \ elsewhere \ \\ \ \ \ \ \ \ \ \ } \right.\)
b)
\(P\bigg[y_1 \ge \dfrac{1}{2}\bigg |y_2 \ge \dfrac{1}{2} \bigg] = \dfrac{P\bigg [y_1 \ge \dfrac{1}{2} . y_2 \ge\dfrac{1}{2} \bigg]}{P\bigg[ y_2 \ge \dfrac{1}{2}\bigg]}\)
\(= \dfrac{\int \limits ^1_{\frac{1}{2}} \int \limits ^1_{\frac{1}{2}} f_{y_1,y_1(y_1-y_2) dy_1dy_2}}{\int \limits ^1_{\frac{1}{2}} fy_1 (y_2) \ dy_2}\)
\(= \dfrac{\int \limits ^1_{\frac{1}{2}} \int \limits ^1_{\frac{1}{2}} (y_1+y_2) \ dy_1 dy_2}{\int \limits ^1_{\frac{1}{2}} (y_2 + \dfrac{1}{2}) \ dy_2}\)
\(= \dfrac{\dfrac{3}{8}}{\dfrac{5}{8}}\)
\(= \dfrac{3}{8}}\times {\dfrac{8}{5}}\)
\(= \dfrac{3}{5}}\)
= 0.6
(c) The required probability is:
\(P(y_2 \ge 0.75 \ y_1 = 0.50) = \dfrac{P(y_2 \ge 0.75 . y_1 =0.50)}{P(y_1 = 0.50)}\)
\(= \dfrac{\int \limits ^1_{0.75} (y_2 +0.50) \ dy_2}{(0.50 + \dfrac{1}{2})}\)
\(= \dfrac{0.34375}{1}\)
= 0.34375
PLS HELP ME!! :((
Find the volume, given that the apothem is 11.3 in. (hint: remember for regular polygons, A = 2 (apothem) (Perimeter) Round your answer to the nearest - tenth.

Answers
Answer:
V = 3085 in³
Step-by-step explanation:
The volume is given by:
\( V = A*h \)
Where:
A: is the area
h: is the height = 7 in
The area of the polygon can be found by using the given equation:
\( A = \frac{1}{2}a*p \)
Where:
a: is the apothem = 11.3 in
p: is the perimeter
The perimeter is:
\( p = 13*6 = 78 in \)
Hence, the volume is:
\( V = A*h = \frac{1}{2}a*p*h = \frac{1}{2}11.3 in*78 in*7 in = 3085 in^{3} \)
I hope it helps you!
112-38 x 14 : 14+ 179 =

Answers
HELP ASAP ILL GIVE BRAINLIEST
Write an expression for
The product of eleven times a number less than 12
11(n - 12)
12n - 11
11n - 12
12 - 11n
Answers
Answer:
11n - 12
Step-by-step explanation:
The answers for the March 22 Recording Check
1. Solve the following one-step equation.
x+5=−7
x = -12 This is the correct answer
x = 2
2. An expression does NOT have an equal sign
The answer would be True
for every 6 brown markers there are 8 green markers.if you have 72 brown markers.how many green markers would you have
Answers
Answer:
93.6
Step-by-step explanation:
93.6 is your actual ans.
if you can write 94 it will be more convenient
Rewrite the function by completing the square.
h (x)=x^2+3x−18
Answers
Answer: (x+6)(x-3)
Step-by-step explanation:
y=x^2+3x-18
(x+6)(x-3 )
Given f(x) and g(x) = k.f(x), use the graph to determine the value of k.
3
3
g(x)
-2+
f(x)
0
-5
-2
-6
3
-1-
a
--2
-3
.
0-2
1
0 - 2
0
.
Question 9 (Not Answered)

Answers
Take y intercepted points of both lines.
f(x)=(0,-2)
g(x)=(0,3)
Now
\(\\ \sf\longmapsto f(x)+k=g(x)\)
\(\\ \sf\longmapsto -2+k=3\)
\(\\ \sf\longmapsto k=3+2\)
\(\\ \sf\longmapsto k=5\)
Done!
help me please zearn

Answers
So radius = diameter/2 = 23.80/2 = 11.9
Circumference formula is 2πR
C = 2 * π * 11.9
= 23.80 * 3.14
= 74.732
The National Assessment of Educational Progress (NAEP) includes a "long-term trend" study that tracks reading and mathematics skills over time, and obtains demographic information. In the 2012 study, a random sample of 9000 17-year-old students was selected.24 The NAEP sample used a multistage design, but the overall effect is quite similar to an SRS of 17-year-olds who are still in school. In the sample, 51% of students had at least one parent who was a college graduate. Estimate, with 99% confidence, the proportion of all 17-year-old students in 2012 who had at least one parent graduate from college.
Answers
Answer:
The 99% confidence interval estimate for the proportion of all 17-year-old students in 2012 who had at least one parent graduate from college is (0.4964, 0.5236).
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the zscore that has a pvalue of \(1 - \frac{\alpha}{2}\).
Sample of 9000, 51% of students had at least one parent who was a college graduate.
This means that \(n = 9000, \pi = 0.51\)
99% confidence level
So \(\alpha = 0.01\), z is the value of Z that has a pvalue of \(1 - \frac{0.01}{2} = 0.995\), so \(Z = 2.575\).
The lower limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.51 - 2.575\sqrt{\frac{0.51*0.49}{9000}} = 0.4964\)
The upper limit of this interval is:
\(\pi + z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.51 + 2.575\sqrt{\frac{0.51*0.49}{9000}} = 0.5236\)
The 99% confidence interval estimate for the proportion of all 17-year-old students in 2012 who had at least one parent graduate from college is (0.4964, 0.5236).
Dmitri wants to cover the top and sides of this box with glass tiles that are 1 cm square. How many tiles will he need? Dmitri will need [Blank] glass tiles. The dimentions are...26 , 15, 8.
Answers
The number of tiles needed to cover the surface area of the box excluding the bottom is: 1,046 tiles.
What is the Surface Area of a Box?The surface area of a box is the area surrounding all its faces. A box has 6 rectangular faces. Therefore, the total surface area of the box equals the sum of all 6 rectangular faces.
What is the Surface Area of a Box?SA = 2(lw + lh + hw), where:
l = lengthw = widthh = height of the boxThe image attached below shows the box Dmitri wants to cover. Since the bottom of the box would be excluded, therefore:
The surface area to be covered = surface area of the box - area of the bottom rectangular face
The surface area to be covered = 2(lw + lh + hw) - (l)(w)
l = 26
w = 15
h = 8
Substitute
The surface area to be covered = 2(l×w + lh + hw) - (l)(w) = 2·(15·26+8·26+8·15) - (26)(15) =
The surface area to be covered = 1436 - 390 = 1,046 cm
Area of one tile = 1 cm square
Number of tiles needed = 1,046/1
Number of tiles needed = 1,046 tiles.
Learn more about Surface Area of a Box on:
https://brainly.com/question/26161002
#SPJ1

According to a Pew Research Center report from 2012, the average commute time to work in California is 27.5 minutes. To investigate whether the small city she lives in has a different average, a California high school student surveys 45 people she knows (her teachers, her parents, and their friends and co-workers) and finds the average commute time for this sample to be 24.33 minutes with a standard deviation of 9.53 minutes. The data are not too skewed. The null and alternative hypotheses of her study are: H0 : µ = 27.5 versus Ha : µ 6= 27.5
Required:
a. Identify the observational units for this study.
b. Identify the variable of interest and state whether it is categorical or quantitative.
c. Identify (in words and using an appropriate symbol) the parameter of interest
d. Use the 2SD approach to find a 95% confidence interval for the parameter.
e. Interpret the interval from part d. in context.
Answers
The product of x and 8 is greater than or equal to -28.
Answers
Answer:
x≥3.5
Step-by-step explanation:
8x ≥-28
x≥-28/8
x≥-3.5
−9, −4, 1, 6, .. aremetric or geometric
Answers
From first principles, find the indicated derivatives

Answers
By definition of the derivative,
\(\displaystyle\frac{dr}{ds} = \lim_{h\to0} \frac{\left(\frac{(s + h)^3}2 + 1\right) - \left(\frac{s^3}2 + 1\right)}{h}\)
\(\displaystyle\frac{dr}{ds} = \lim_{h\to0} \frac{\left(\frac{s^3+3s^2h+3sh^2+h^3}2 + 1\right) - \left(\frac{s^3}2 + 1\right)}{h}\)
\(\displaystyle\frac{dr}{ds} = \lim_{h\to0} \frac{\frac{3s^2h+3sh^2+h^3}2}{h}\)
\(\displaystyle\frac{dr}{ds} = \lim_{h\to0} \frac12 \frac{3s^2h+3sh^2+h^3}{h}\)
\(\displaystyle\frac{dr}{ds} = \lim_{h\to0} \frac12 (3s^2+3sh+h^2)\)
\(\displaystyle\frac{dr}{ds} = \frac{3s^2}2\)
hellppppppp pleaseeee

Answers
Answer:
556
Step-by-step explanation:
2*(17*4 + 17*10 + 4*10)
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
Is -4 a irrational number?
Answers
Answer:
No.
Step-by-step explanation:
Irrational numbers are numbers that you can't solve like 3 squared. See you can't find the end of 3 squared, the numbers will go on forever just like pi.

Answer:
No
Step-by-step explanation:
A rational number can be written as the ratio of integers
-4/-1 = -4
This is a rational number
The ———— is used to determine the left-hand and right-hand behavior of the graph of a polynomial function.
--Select-
Behavior Test
t Answ Polynomial Test
Odd Degree Test
Horizontal Line Test
Leading Coefficient Test
Dints] Distinct Zero Test
Even Degree Test
Vertical Line Test
AT10 3.2.001.
Answers
Answer:
I think it is the vertical line test. If you have any other questions let me know! :)
52. Find a vector v whose magnitude is 3 and whose component in the i direction is equal to the component in the j direction.
Answers
The vector whose magnitude is 3 and whose components I. the I and j direction are equal is; <3√2/2i, 3√2/2j>.
Which vector is as described in the task content above?It follows that the magnitude of a vector in terms of its components in the i and j direction is;
M = √(x² + y²).
On this note, since the i and j components are equal; x = y and hence, we have;
3 = √(x² + x²).
3² = 2x²
x² = 9/2
x = 3/√2
x = 3√2/2
On this note, the required vector which is as described is; <3√2/2i, 3√2/2j>.
Read more on vector components;
https://brainly.com/question/26187714
#SPJ1
Cquation
Question 2 of 5
How many solutions does 6 -3x = 12 - 6x have?
A. Infinitely many solutions
B. Two solutions
C. One solution
D. No solutions
Answers
None None None None None None None None None None None None
Answers
Answer:
??
Step-by-step explanation:
17.
Which of the following are equiangular quadrilaterals?
a. parallelogram and rectangle
b. trapezoid and rhombus
c. square and rhombus
d. square and rectangle
e. none of these
Answers
In which
situation can the Expression
on 8×2 be used to find the total number of head wraps on the shelf
Answers
The expression 8×2 can be used to find the total number of head wraps on the shelf when there are 8 head wraps per shelf and 2 shelves in total, resulting in a total of 16 head wraps.
What is expression?Expression in mathematics is a combination of symbols and numbers, often using an operation, such as addition, subtraction, multiplication, or division. It can represent a number, a variable, a function, or a mathematical statement. It can also represent a combination of these things. Expressions are used to describe relationships between numbers, variables, and mathematical concepts.
The expression 8×2 can be used to find the total number of head wraps on the shelf when there are 8 head wraps per shelf and there are 2 shelves in total. This expression can be used to calculate the total number of head wraps on the shelves by multiplying 8 (the number of head wraps per shelf) by 2 (the number of shelves). As such, the expression 8×2 can be used to find the total number of head wraps on the shelf when there are 8 head wraps per shelf and 2 shelves in total, resulting in a total of 16 head wraps.
In conclusion, the expression 8x2 can be used to calculate the total number of head wraps on the shelf when there are 8 head wraps per shelf and 2 shelves in total. By multiplying 8 (the number of head wraps per shelf) by 2 (the number of shelves), the total number of head wraps on the shelf can be found, resulting in a total of 16 head wraps.
To know more about expression click-
http://brainly.com/question/1859113
#SPJ1
Complete questions as follows-
In which situation can the Expression
on 8×2 be used to find the total number of head wraps on the shelf?
What is the sum? -1.5 + 1.9
Answers
Answer: 0.4
Step-by-step explanation:
Answer:
0.4
Step-by-step explanation:
Took the test
Using the Pythagorean Theorem, prove whether or not the following triangle is a right
triangle. Remember to show your work.
A triangle with side lengths of 13m, 5m and 10m
A) Is it a right triangle (1 point)
B) Explain and show your work (4 points)

Answers
A) The triangle is not a right triangle.
B) Based on the calculations, the square of the longest side is not equal to the sum of the squares of the other two sides, indicating that the triangle does not meet the criteria of a right triangle according to the Pythagorean Theorem.
To determine if the triangle with side lengths 13m, 5m, and 10m is a right triangle, we can apply the Pythagorean Theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Let's calculate the squares of the side lengths:
13^2 = 169
5^2 = 25
10^2 = 100
According to the Pythagorean Theorem, if this triangle is a right triangle, the square of the longest side (13^2 = 169) should be equal to the sum of the squares of the other two sides (5^2 + 10^2 = 25 + 100 = 125).
Since 169 is not equal to 125, we can conclude that the triangle with side lengths 13m, 5m, and 10m is not a right triangle. The sum of the squares of the shorter sides is less than the square of the longest side, which does not satisfy the condition for a right triangle.
For more such questions on Pythagorean Theorem
https://brainly.com/question/343682
#SPJ8
solve the inequality-2+4x<14
Answers
Answer: x<4
Step-by-step explanation:
If we break this down as
-2+4x<14 and we add 2 to both sides
4x+<16 and divide by 4
and you get x<4
ok here you go guyysss

Answers
Answer:
Option B will be your answer
Step-by-step explanation:
I hope this helps u have a great day ^_^

